Stability analysis of time-varying systems via parameter-dependent homogeneous Lyapunov functions

Zhang Huasheng Zhang Kanjian

(1Key Laboratory of Measurement and Control of Complex Systems of Engineering of Ministry of Education,Southeast University, Nanjing 210096, China)(2School of Automation, Southeast University, Nanjing 210096, China)(3School of Mathematical Sciences, Liaocheng University, Liaocheng 252000, China)



Stability analysis of time-varying systems via parameter-dependent homogeneous Lyapunov functions

Zhang Huasheng1,2,3Zhang Kanjian1,2

(1Key Laboratory of Measurement and Control of Complex Systems of Engineering of Ministry of Education,Southeast University, Nanjing 210096, China)(2School of Automation, Southeast University, Nanjing 210096, China)(3School of Mathematical Sciences, Liaocheng University, Liaocheng 252000, China)

This paper considers the stability analysis of linear continuous-time systems, and that the dynamic matrices are affected by uncertain time-varying parameters, which are assumed to be bounded, continuously differentiable, with bounded rates of variation. First, sufficient conditions of stability for time-varying systems are given by the commonly used parameter-dependent quadratic Lyapunov function. Moreover, the use of homogeneous polynomial Lyapunov functions for the stability analysis of the linear system subject to the time-varying parametric uncertainty is introduced. Sufficient conditions to determine the sought after Lyapunov function is derived via a suitable paramenterization of polynomial homogeneous forms. A numerical example is given to illustrate that the stability conditions are less conservative than similar tests in the literature.

linear time-varying systems; polytopic uncertainty; robust stability; linear matrix inequality

The study of linear time-varying system stability has been an important issue in control theory for many years. It is well known that quadratic stability is a sufficient condition for the stability of linear systems with arbitrarily fast time-varying parameters. This condition is appealing from a numerical point of view mainly because of its simplicity, and it has been widely used for robust control and robust filter design, in most cases through convex problems formulated in terms of linear matrix inequalities (LMIs)[1-2]. In order to reduce conservativeness, more general classes of Lyapunov functions have been considered, including polyhedral Lyapunov functions[3-4], piecewise quadratic Lyapunov functions[5], and homogeneous polynomial Lyapunov functions (HPLFs)[6-7].

Homogeneous polynomial Lyapunov functions are a viable alternative to the above classes of Lyapunov functions. In fact, that this class of Lyapunov functions can improve the robust stability results provided by quadratic Lyapunov functions has been recognized for a long time[8]. Recently, it has been shown that for these systems, robust stability is equivalent to the existence of a smooth Lyapunov function that turns out to be the sum of the squares of homogeneous polynomial forms[9-10].

This paper focuses on the stability analysis of linear systems where dynamic matrices are affected by uncertain time-varying parameters with a bounded variation rate. The problem can be tackled by HPLFs and constructing HPLFs can be formulated in terms of special convex optimization techniques based on linear matrix inequalities (LMI). An example here is shown, which proves that HPLFs are powerful tools for stability analysis.

1 Problem Formulation and Preliminaries

Consider the linear time-varying system

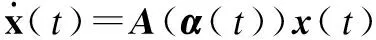
(1)

wherex(t)∈Rnis the state andA(α(t))∈Rn×nis an uncertain time-varying matrix belonging to the polytopeΛgiven by

In other words, for allt>0 with components,αj(t) represents time varying unknown parametric perturbations such thatA(α(t))∈co{A1,…,AN}, where co{·} denotes the convex hull.

The parameters of this system are assumed to have bounded time-derivatives, i.e.,

(2)

The functionfm(x) is a homogeneous form of degreeminx∈Rnif

wherei1,i2, …,inare non-negative integers, andci1i2…imare the weighting coefficient. The formfm(x) is said to be positive iffm(x)>0, ∀x≠0.

The following result provides a sufficient condition for establishing the existence of an HPLF of degree 2mfor system (1).

Lmma 1[11]LetAj,{m}denote the extended matrix ofAj. If the system of the LMIs

admits a feasible solutionV=VT∈Rn×n, thenv2m(x)=x{m}TVx{m}is an HPLP for Eq.(1).

The next lemma presents a sufficient LMI condition for the robust stability of linear time-varying systems in the polytopic form of Eq.(1).

Lmma 2[12]For given real scalarsρi>0,i=1,2,…,N-1, if there exist symmetric positive definite matricesPj∈Rn×n,j=1,2,…,N, satisfying

(3)

j=1,2,…,N-1;k=j+1,…,N

(4)

then the system (1) is asymptotically stable for all time-varying uncertain parameters inside the polytopeΛrespecting the time-derivative constraints (2) with the parameter dependent Lyapunov matrix given by

2 Main Results

The main result of the paper is a sufficient condition to determine the sought Lyapunov function, which amounts to solving an LMI feasibility problem, derived via a suitable parameterization of homogeneous polynomial forms.

Theorem 1 For given real scalarsρi>0,i=1,2,…,N-1, if there exist symmetric positive definite matricesPij∈Rn×n,j=1,2,…,N, satisfying

(5)

PNk+2(Pij-PNj))<0

(6)

ρi(Pij-PNj+2(Pik-PNk))<0

(7)

(8)

Proof Consider the quadratically parameter-dependent Lyapunov function v(x)=xTP(α)xwith

i,j=1,2,…,N

whereP(α(t))=P(α(t))T. It is clear thatP(α(t)) is a positive definite parameter dependent Lyapunov matrix.

Observing that

we have

(9)

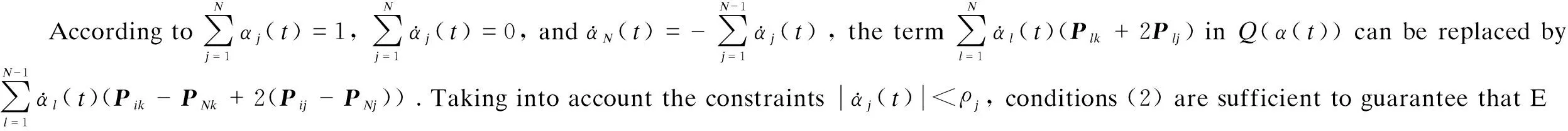
In the caseN=2 (two vertices) of Theorem 1, a simpler formulation can be obtained as

Following the ideas of square matricial representations (SMR) of homogeneous forms and Lemma 2, a new sufficient condition based on homogeneous parameter-dependent Lyapunov functions is stated in the next theorem.

Theorem 2 LetAj,{m}andPij,{m}denote the extended matrix ofAjandPij, respectively. Then, the system (1) is asymptotically stable ifPij exists,{m}>0 exists, such that the following set of LMIs is satisfied:

(10)

(11)

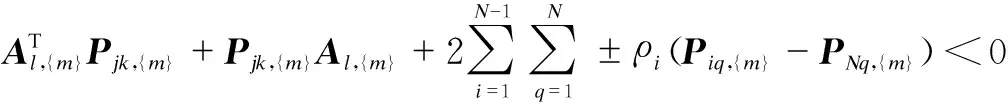
(12)

(13)

wherek=2,3,…,N;l=2,3,…,N.

Proof According to Lemma 1, letv2m(x)=x{m}T·P(α){m}x{m}be the HPLF of the system (1).

By differentiatingv2m(x) along the trajectories of the system and exploiting the properties of SMR, we can obtain

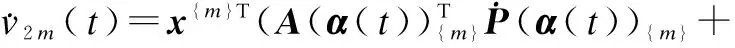
x{m}TQ(α(t))x{m}

With a similar approach as proof of Theorem 1, we can obtain (10), (11), (12) and (13).

Several remarks can be given on the results above.

Remark 1 The conditions of Theorem 2 are used more for scalar variables in the tests (10) to (13) than in the tests of Lemma 2 and Theorem 1, which can provide less conservative evaluations of stability at the price of a slightly higher numerical complexity.

Remark 2 The family of HPLFs in the casem=1, which have been considered by Theorem 1, can be reduced to quadratic Lyapunov functions with affine parameter dependence. The condition provided by Theorem 2 is based on the SMR of homogeneous polynomial forms.

3 Numberical Example

Example 1 The following second-order linear differential equation is considered:

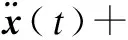
(14)

Fig.1 shows the regions of stability below of each curve provided by Ref.[14] (dashed line), and Theorem 2 in the casem=2 (solid line), respectively, calculated with an LMI solver that verifies the feasibility of each stability condition. The same example was also considered in Ref.[15], which gives the limits of stability corresponding to the region of the plane (ω=4 andδ=0.23). The limits of stability corresponding to the region of the plane are:ω=4 andδ=0.27. It is to be noted that an important improvement is when the present result is compared with Ref.[15].

Fig.1 Stability regions

4 Conclusion

In this paper, we introduce some new stability conditions for time-varying continuous-time polytopic systems using homogeneous Lyapunov functions. With respect to previous work on this class of Lyapunov functions, better results have been obtained by exploiting a complete parameterization of homogeneous forms of a given degree. Compared with some previous stability conditions, the main results via HPDFs in this paper have less conservatism. An numerical example is proposed to show less conservativeness with some existing results.

[1]El Ghaoui L, Niculescu S I.Advancesinlinearmatrixinequalitymethodsincontrol[M]. Philadelphia: Advances in Design and Control, 2000.

[2]Lacerda M J, Oliveira R C L F, Peres P L D. RobustH2andH∞filter design for uncertain linear systems via LMIs and polynomial matrices [J].SignalProcessing, 2011, 91(5): 1115-1122.

[3]Montagner V F, Oliveira R C L F, Peres P L D, et al. Stability analysis and gain scheduled state feedback control for continuous time systems with bounded parameter variations[J].InternationalJournalofControl, 2009, 82(6):1045-1059.

[4]Ambrosino R, Ariola M, Amato F. A convex condition for robust stability analysis via polyhedral Lyapunov functions [J].SIAMJControlOptim, 2012, 50(1): 490-506.

[5]BenAbdallah A, Hammami M A, Kallel J. Robust stability of uncertain piecewise-linear systems: LMI approach [J].NonlinearDyn, 2011, 63(1/2): 183-192.

[6]Chesi G, Garulli A, Tesi A, et al. Homogeneous Lyapunov functions for systems with structured uncertainties [J].Automatic, 2003, 39(6): 1027-1035.

[7]Chesi G. Robust stability of time-varying uncertain systems with rational dependence on the uncertainty [J].IEEETransactionsonAutomaticControl, 2010, 55(10): 2353-2357.

[8]Brockett R W.LiealgebraandLiegroupsincontroltheory[M]. Netherlands: Springer, 1973.

[9]Prajna S, Papachristodoulou A, Seiler P, et. al. New developments in sum of squares optimization and SOSTOOLS [C]//Proceedingsofthe2004AmericanControlConference. Boston, USA, 2004:5606-5611.

[10]Ahmadi A A, Parrilo P A. Converse results on existence of sum of squares Lyapunov functions [C]//IEEEConferenceonDecisionandControlandEuropeanControlConference(CDC-ECC). Orlando, FL, USA, 2011: 6516-6521.

[11]Chesi G, Garulli A, Tesi A, et al.Homogeneouspolynomialformsforrobustnessanalysisofuncertainsystems[M]. Heidelberg: Springer, 2009.

[12]Montagner V E, Peres P L D. A new LMI condition for the robust stability of linear time-varying systems [C]//Proceedingsofthe42ndIEEEConferenceonDecisionandControl. Maui, Hawaii, USA, 2003:6133-6138.

[13]Montagner V E, Peres P L D. Robust stability and H1 performance of linear time-varying systems in polytopic domains [J].IntJControl, 2004, 77(15): 1343-1352.

[14]Geromel J C, Colaneri P. Robust stability of time varying polytopic systems [J].SystemsandControlLetters, 2006, 55(1): 81-85.

[15]Aouani N, Salhi S, Garcia G, et al. New robust stability and stabilizability conditions for linear parameter time varying polytopic systems [C]//The3rdInternationalConferenceonSignals,CircuitsandSystems. Medenine, Tunisia, 2009: 1-6.

基于参数依赖齐次多项式的时变系统稳定性分析

张化生1,2,3张侃健1,2

(1东南大学复杂工程系统测量与控制教育部重点实验室,南京210096)(2东南大学自动化学院，南京210096)(3聊城大学数学科学学院,聊城252000)

基于齐次多项式Lyapunov函数这一新工具研究了时变不确定系统鲁棒稳定性问题.针对常见的含参数时变且有界连续可微线性系统的最大稳定区域问题，首先构造常用的参数依赖二次Lyapunov函数,进而给出一个时变系统稳定的充分条件.然后,通过构造适合的参数依赖齐次Lyapunov函数,并利用齐次多项式矩阵表示方法,最终以线性不等式的形式给出系统全局渐近稳定的一个充分条件.数值仿真结果表明齐次Lyapunov函数方法得到的结论对于某些系统比之前类似文献具有更小的保守性.

线性时变系统;多面体不确定性;鲁棒稳定性;线性不等式

TP202.1;TP271.7

s：The Major Program of National Natural Science Foundation of China (No.11190015), the National Natural Science Foundation of China (No.61374006).

：Zhang Huasheng, Zhang Kanjian. Stability analysis of time-varying systems via parameter-dependent homogeneous Lyapunov functions [J]．Journal of Southeast University (English Edition),2014,30(3):302-305．

10.3969/j.issn.1003-7985.2014.03.008

10.3969/j.issn.1003-7985.2014.03.008

Received 2013-12-19.

Biographies：Zhang Huasheng (1978—), male, doctor, zhsh0510@163.com; Zhang Kanjian (1971—), male, doctor, professor, kjzhang@seu.edu.cn.