基于遗传算法的摄像机内部参数标定优化方法
徐中宇, 李春龙, 孙秋成, 宁 闯
(1.长春工业大学 计算机科学与工程学院, 长春 130012; 2.长春工业大学 基础科学学院, 长春 130012)
基于遗传算法的摄像机内部参数标定优化方法
徐中宇1, 李春龙1, 孙秋成2, 宁 闯1
(1.长春工业大学 计算机科学与工程学院, 长春 130012; 2.长春工业大学 基础科学学院, 长春 130012)
基于张正友标定法, 提出一种新的基于遗传算法的摄像机内部参数标定优化方法.该方法能矫正传统摄像机标定不可靠的初始化和容易陷入局部最优解而带来的精度损失, 提高了摄像机内部参数的标定精度.通过与张正友标定法进行比较, 证明了该方法性能稳定, 能快速、准确地标定摄像机内部参数.
摄像机标定; 遗传算法; 内参优化
高精度工业测量和新兴3D打印等技术, 对计算机视觉测量的精度提出了更高要求, 而摄像机标定的结果直接影响视觉测量的精确性[1-2].因此, 提高摄像机标定精度是机器视觉在实际应用中最关键的问题.
现有的摄像机标定技术分为传统摄像机标定技术、基于主动视觉的标定方法和摄像机自标定3类[3].当应用场合对标定精度要求较高时, 传统标定法有其不可取代的作用.目前应用较广泛的标定方法主要有Tsai两步标定法[4]、张正友标定法[3]和胡占义等[5]提出的基于外极点的正交运动法.其中张正友标定法使用2D标定平面, 降低了标定成本, 具有较高的求解速度和标定精度.但由于其使用基于线性模型估计畸变参数的方法, 因此很难可靠地初始化[6], 且因非线性优化算法的局限性, 该方法存在陷入局部最优的可能, 从而降低了标定精度.
基于此, 本文结合张正友标定方法和遗传算法的优点, 提出一种新的基于遗传算法的摄像机内参优化方法.遗传算法模拟生物进化过程中的遗传变异过程, 使用染色体对解空间中的种群编码, 在仅知道目标函数的条件下即可迅速找到全局最优解[7].实验证明该方法准确、可行.
1 标定模型
摄像机标定模型涉及世界坐标系(Ow,Xw,Yw,Zw)、摄像机坐标系(Oc,Xc,Yc,Zc)、图像坐标系(o1,x,y)和图像像素坐标系(o1,u,v)[1], 如图1所示.
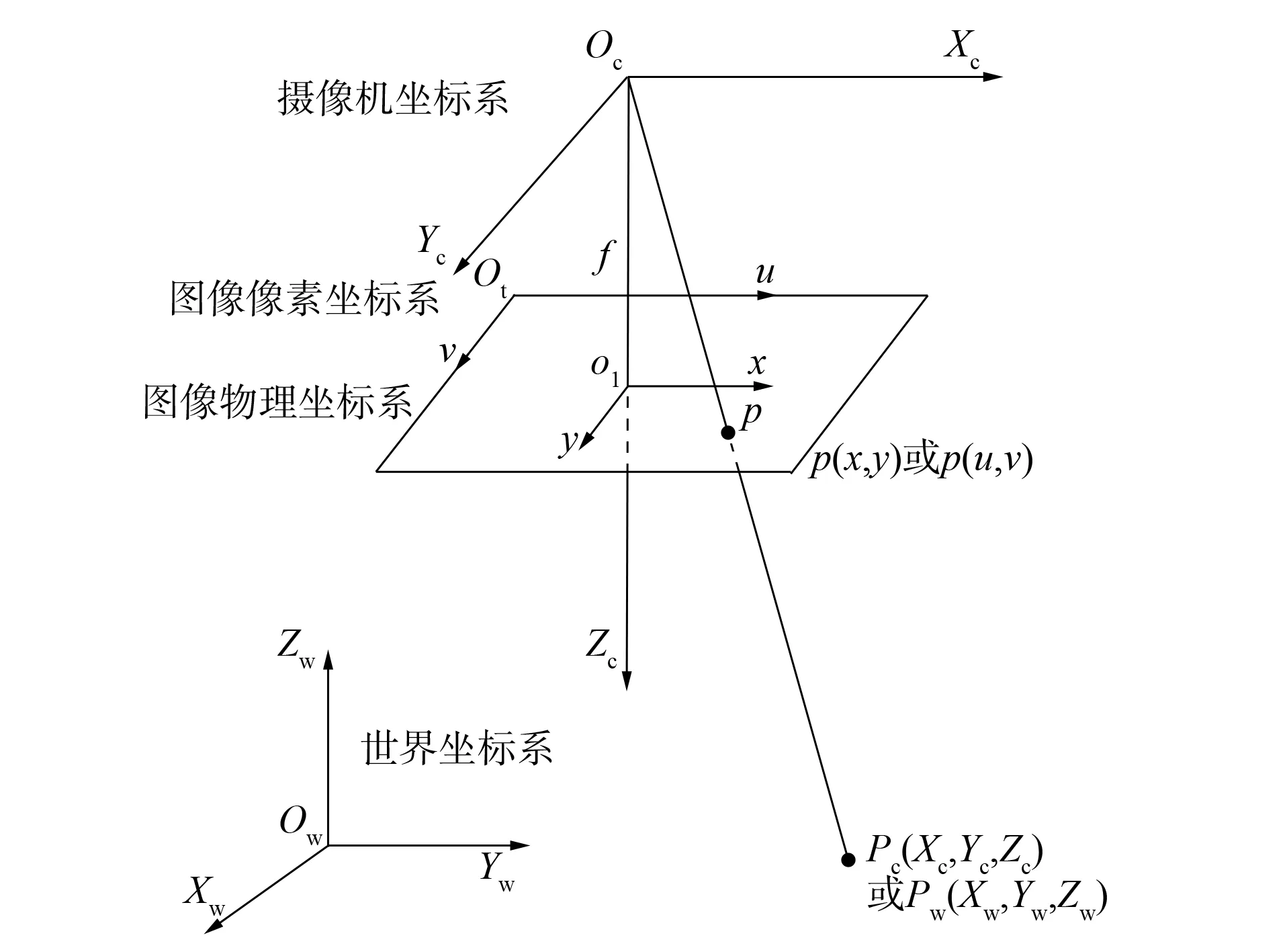
图1 摄像机模型坐标系Fig.1 Coordinate system of camera model
引入归一化齐次图像坐标后, 通常任一空间点Pw(Xw,Yw,Zw)到图像像素坐标p(u,v)下的线性变换模型可表示为
其中:α=f/dx;β=f/dy; (u0,v0)为摄像机像素平面主点坐标;γ为图像坐标系u轴、ν轴的不垂直因子;M1为内部参数矩阵; (Rt)为外部参数;M2为外部参数矩阵.
由于镜头畸变会导致空间点在成像过程中存在不同程度的非线性变形, 因此通常情况下, 理想平面图像坐标点(xu,yu)可表示为实际图像坐标点(xd,xd)与畸变误差之和[8], 即
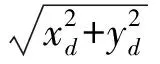
2 求解摄像机模型内参初始值


其中λ为比例因子.利用r1和r2的正交性可得下列约束:
由于一个单应性矩阵H有8个自由度, 而外部参数有6个(3个旋转, 3个平移), 因此从一个转换矩阵只能获得关于摄像机内部参数的两个约束.A-TA-1实际上描述了图像的绝对二次曲线在图像平面的投影[9].求解H是一个非线性最小二乘问题, 可用梯度法、Gauss牛顿法或Levenberg-Marquardt等非线性优化方法.令
由于B是对称矩阵, 因此可表示为b=(B11,B12,B22,B13,B23,B33)T, 如果实验中使用了n幅图像, 则每幅图像都会得到对应的两个约束方程, 即有Vb=0, 其中V是一个2n×6的矩阵.如果n≥3, 可得到方程的唯一解b.确定b值后, 通过式(6)易求得内部参数矩阵A中各元素的值:
3 基于遗传算法的内参优化
遗传算法执行过程中, 处理经过编码的个体而不是参数本身, 摒弃了传统搜索算法中单点搜索的劣势, 采用多个个体同时参与处理的方式, 减少了陷入局部最优解的风险.此外, 遗传算法的个体评价机制只使用适应度函数完成, 不受函数本身是否连续或可微的影响.
遗传算法是解决摄像机标定这类多参数、大范围、非线性优化问题的一种可行方法.标准遗传算法用于高维空间(参数个数大于10)的寻优时性能会变差, 且随着搜索空间维数的增加, 算法性能会急剧退化[10].基于此, 人们提出了外参固定的优化模型, 降低了优化函数的维数, 避免了遗传算法的不足.同时, 在合理的范围内扩展计算得到的内参初始值, 作为遗传算法优化的搜索范围, 使内参的优化结果更可信.
使用遗传算法优化下列目标函数:
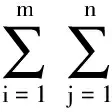
本文优化算法描述如下:
1) 初始化种群.在张正友标定算法计算出的初始值基础上, 随机产生包含输入参量(A,k1,k2,p1,p2)的N个个体群, 每个个体群包含M个个体作为初始群体P(0).
2) 确定编码方式.编码是使用不同的编码方式, 将目标函数的可行域(表现型)转化为遗传算法可使用基因型的过程, 不同的编码方式适用于不同的目标函数优化[11].因为该优化问题维数(参数)较高, 搜索范围较大, 故利用浮点数编码方式进行编码, 可在优化过程中避免二进制编码对参数进行的编码和译码过程, 从而降低了编码、译码对精度的损伤.
3) 建立适应度函数.适应度值是评价每个个体在整个群体中健壮性的重要标志, 遗传算法要求个体适应度必须为正或零, 故建立如下适应度函数:
其中:f(x)为目标函数;Cmax为估计最大值.
4) 选择策略.每个个体的适应度值都标示了自己在群体中的位置, 根据群体中个体的适应值, 按赌轮盘选择策略计算其相对适应值:
其中fi表示当前进化代数群体中第i个个体的适应值.每个个体遗传到下一代的繁殖量为Ni=round(reli·N), 其中: round(x)表示最接近x的整数;N为群体的规模.
5) 交叉运算.设定交叉概率Pc, 随机组合第t代群体P(t)内的个体, 对每个个体以概率Pc交换它们之间的部分染色体.针对选中的两个个体x1,x2进行如下交叉:


6) 变异运算.设定遗传算法变异概率Pm可根据适应度值大小而改变[12], 以概率Pm将变异算子作用于群体, 计算得到参与变异操作的个体数量.对群体P(t)中选择的个体, 改变其某一个或某一些基因座上的基因值为其他等位基因.群体P(t)经过选择、交叉、变异运算后得到下一代群体P(t+1).
7) 算法终止.当迭代次数达到预设的代数, 或最优个体的适应度达到给定的阈值, 或最优个体的适应度和群体适应度不再上升时, 算法终止.
算法运算结束得到优化后的摄像机内部参数.
4 实验分析
下面通过实验验证本文标定方法的准确性及可行性.实验中, 使用焦距为8 mm的定焦工业镜头, 从不同方向对NANO CBC200 MM-5.0型标定面板(外形: 200 mm×200 mm×3.0 mm; 图形: 棋盘格5.0 mm×5.0 mm, 精度1 μm)拍摄5幅图像(1 376×1 024像素).使用张正友标定法计算出内参初始值, 结果列于表1.

表1 摄像机内参标定初始值Table 1 Initial value of intrinsic parameter of camera
当标定结果与摄像机及标定板所处位置无关时, 可假设摄像机坐标为世界坐标, 拍摄2幅图像用于内参优化.在上述初始值的基础上结合各参数的属性, 在合理范围内扩展其范围作为遗传算法的搜索范围, 结果列于表2.
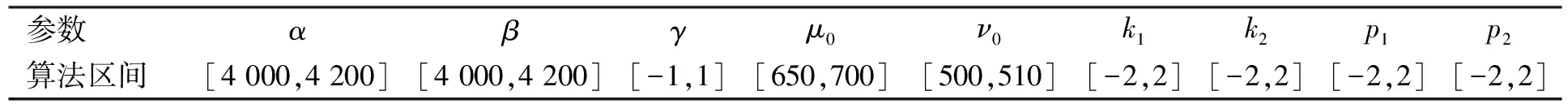
表2 内参初始值及遗传算法搜索区间Table 2 Initial value and the genetic algorithm search range
遗传算法初始种群在表2所列范围内随机产生, 并使用浮点数编码方法对其编码.设置种群规模M=100, 算法终止代数T=150, 并采用自适应的交叉和变异概率.基于MATLAB遗传算法工具箱函数[13]编程, 分别对2幅图像进行内参的最优化修正.经过多次实验并取其平均值, 可得理想的内参最优化结果.将实验所得结果与张正友标定法得到的结果进行比较, 结果列于表3.分别计算其二次投影误差, 结果如图2和图3所示.图2为张正友标定法在x轴和y轴方向得到的二次投影误差, 其平均误差为err=(0.039 76,0.042 34).图3是本文方法在x轴和y轴方向得到的二次投影误差, 其平均误差为err=(0.033 14,0.035 40).通过与张正友的标定结果比较可知, 本文提出的方法具有一定的可行性, 且优化效率更高.

表3 采用两种实验方法得到的内参数值Table 3 Internal parameter values obtained by two experimental methods

图2 张正友标定法投影误差Fig.2 Projection error of Zhang’s method
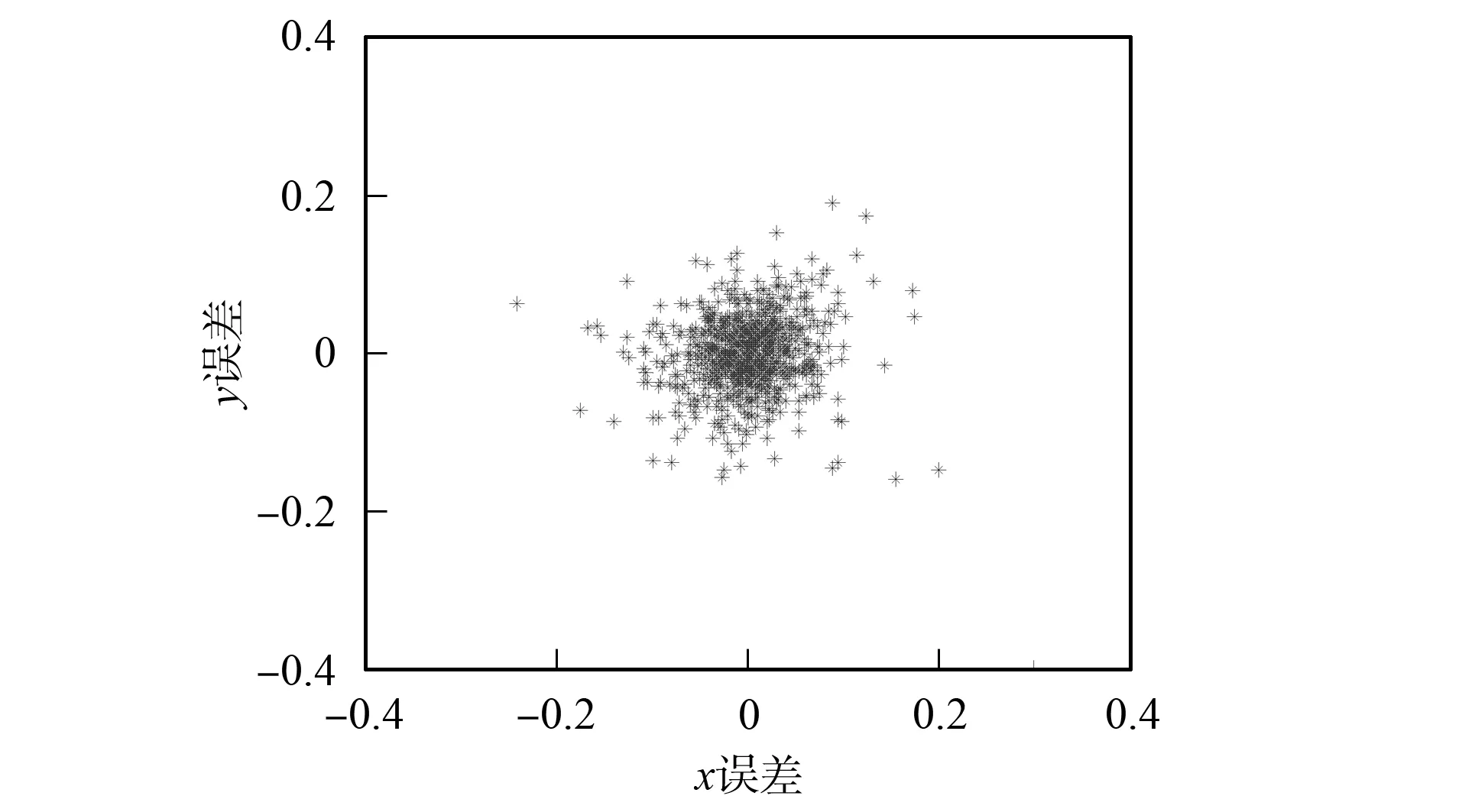
图3 本文标定法投影误差Fig.3 Projection error of the present method
综上所述, 本文在充分考虑了标定模型的初始化问题和传统非线性优化方法的局限性基础上, 结合遗传算法强大的全局搜索能力, 提出了一种新的基于遗传算法的摄像机自标定内参优化方法.在模型初始化过程中, 使用张正友标定方法保证了计算的内外参初始值真实可信; 在模型优化中固定外参以降低遗传算法的搜索维度; 在初始值范围内确定搜索范围, 以缩小遗传算法的搜索空间; 实验中多次测量保证了实验数据的准确性.实验结果表明, 本文提出的摄像机内参优化方法是可行的, 不仅提高了标定精度, 且更便捷.
[1]马颂德, 张正友.计算机视觉: 计算理论与算法基础 [M].北京: 科学出版社, 2003: 51-70.(MA Songde, ZHANG Zhengyou.Computer Vision: Computer Theory and Algorithms Based [M].Beijing: Science Press, 2003: 51-70.)
[2]张广军.机器视觉 [M].北京: 科学出版社, 2005: 14-97.(ZHANG Guangjun.Machine Vision [M].Beijing: Science Press, 2005: 14-97.)
[3]ZHANG Zhengyou.A Flexible New Technique for Camera Calibration [J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.
[4]Tsai R Y.A Versatile Camera Calibration Technique for High-Accuracy 3D Machine Vision Metrology Using Off-the-Shelf TV Cameras and Lenses [J].IEEE Journal of Robotics Automation, 1987, 3(4): 323-344.
[5]胡占义, 吴福朝.基于主动视觉摄像机标定方法 [J].计算机学报, 2002, 25(11): 1149-1156.(HU Zhanyi,WU Fuchao.A Review on Some Active Vision Based Camera Calibration Techniques [J].Chinese Journal of Computers, 2002, 25(11): 1149-1156.)
[6]Schreier H W, Garcia D, Sutton M A.Advances in Light Microscope Stereo Vision [J].Experimental Mechanics, 2004, 44(3): 278-288.
[7]Murthy C A.Genetic Algorithms: Basic Principles and Applications [C]//Proceedings of 2012 IEEE Computational Intelligence and Signal Processing (CISP 2012).Guwahati, Assam, India: IEEE, 2012: 22.
[8]WENG Juyang, Paul C, Marc H.Camera Calibration with Distortion Models and Accuracy Evaluation [J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(10): 965-980.
[9]LIU Ding, WU Xiongjun, YANG Yanxi.An Improved Self-calibration Approach Based on Adaptive Genetic Algorithm for Position-Based Visual Servo [J].Journal of Control Theory and Applications, 2008, 6(3): 246-252.
[10]TANG Kezong, YANG Jingyu, CHEN Haiyan, et al.Improved Genetic Algorithm for Nonlinear Programming Problems [J].Journal of Systems Engineering and Electronics, 2011, 22(3): 540-546.
[11]ZHANG Yi, ZHAO Jun.Priority-Based Encoding Genetic Algorithm for Solving Two-Stage Capacitated Facility Location Problem with Side Constraints [C]//Proceedings of 2011 IEEE International Conference on Intelligent Computing and Intelligent Systems (ICIS 2011).Beijing: IEEE, 2011: 72-75.
[12]HU Fengge, ZHANG Jianhua, FANG Liye.Sparse Planar Retrodirective Antenna Array Using Improved Adaptive Genetic Algorithm [J].Journal of Electronic Science and Technology, 2011, 9(3): 265-269.
[13]雷英杰, 张善文, 李续武.MATLAB遗传算法工具箱及应用 [M].西安: 西安电子科技大学出版社, 2005.(LEI Yingjie, ZHANG Shanwen, LI Xuwu.MATLAB Genetic Algorithm Toolbox and Applications [M].Xi’an: Xidian University Press, 2005.)
InternalParameterOptimizingMethodofCameraCalibrationBasedonGeneticAlgorithm
XU Zhongyu1, LI Chunlong1, SUN Qiucheng2, NING Chuang1
(1.SchoolofComputerScienceandEngineering,ChangchunUniversityofTechnology,Changchun130012,China;
2.SchoolofBasicScience,ChangchunUniversityofTechnology,Changchun130012,China)
An internal parameter optimizing method of camera calibration based on genetic algorithm was proposed.This method is a re-amendment of internal parameter obtained by Zhang Zhengyou calibration.It can rectify the loss of precision caused by unreliable initialization and locally optimal solution and improve the calibration precision of interior parameters of the camera.The result shows that the performance of this method is stable.It can quickly and accurately calibrate the camera internal parameters.
camera self-calibration; genetic algorithm; internal optimization
2013-11-07.
徐中宇(1971—), 男, 汉族, 博士, 副教授, 从事图像处理和生物认证的研究, E-mail: xuzhongyu01@126.com.通信作者: 李春龙(1987—), 男, 汉族, 硕士研究生, 从事数字图像处理的研究, E-mail: 408534325@qq.com.
吉林省教育厅“十一五”科学技术研究项目(批准号: 吉教科合字[2010]第295号).
TP391.4
A
1671-5489(2014)06-1267-05
10.13413/j.cnki.jdxblxb.2014.06.30
韩 啸)

