再生型颤振系统的Hopf分岔分析与控制
李鹏松, 盛桂全, 孟永永
(东北电力大学 理学院, 吉林 吉林 132012)
(2iωc+2ζ+ωcτe-iωcτ)A′-2iδζA+HA2=0,(17)
再生型颤振系统的Hopf分岔分析与控制
李鹏松, 盛桂全, 孟永永
(东北电力大学 理学院, 吉林 吉林 132012)
考虑一类单自由度的非线性再生型切削颤振系统, 利用多尺度法分析系统时滞参数对解稳定性的影响, 并在此基础上采用非线性位移反馈控制抑制Hopf分岔引起的颤振.理论分析和数值模拟结果验证了所给控制方法在切削颤振控制模型中的有效性.
亚临界Hopf分岔; 超临界Hopf分岔; 非线性控制; 多尺度法

图1 刀具切削过程中的再生效应Fig.1 Regeneration effect of cutting process
机床、刀具和工件形成一个复杂的动力学结构, 在某种条件下, 系统会发生剧烈的振动.可将这种振动分成三类: 自由振动、强迫振动、自激振动.在机床动力学领域自激振动也称为“颤振”.常见的颤振主要有由速度反馈引起的切削颤振、模态藕合引起的切削颤振以及再生型机理因素引起的颤振.在工件材料切削过程中发生颤振, 常会使加工过程变得不稳定, 导致加工表面质量和金属切削率下降, 严重时甚至会破坏刀具和机床.研究表明, 切削过程中的再生效应是引起颤振的主要原因[1-4].一些外部扰动或工件表面的一个斑点即可引起切削力的微小变化, 从而导致动力系统的振动, 振动可在工件表面留下波纹状的切削痕迹, 如图1所示.波纹状的表面将影响后续的切削, 当刀具从工件表面切除薄片时, 振动导致薄片不平.如果振动振幅不断衰退, 切削过程即为稳定的.但在某种情况下, 振幅会变大, 同时产生颤振, 这种现象称为再生型颤振.发生再生型颤振的系统, 通常因时滞参数变化导致平衡点失稳而引起Hopf分岔.因此, 研究再生型颤振系统离不开对Hopf分岔的研究[5-10].本文主要分析再生颤振系统在不同主轴旋转周期情况下的运动稳定性, 对系统失稳的过程进行分岔分析及类型判定, 对发生Hopf分岔的系统设计合理的控制器, 从而将系统控制到稳定, 并通过实际算例和仿真分析验证所设计控制器的实用性和有效性.
1 再生型颤振系统
Hanna等[11]针对刀具切削系统, 提出了非线性再生型颤振理论, 并建立了单自由度无量纲形式的振动方程

其中:xτ=x(t-τ),x(t)表示切削刀具尖端动态位移,τ表示主轴的旋转周期;ζ是阻尼比;w是切割宽度;α2和α3表示非线性切削力的系数.系统(1)的线性形式为
若式(2)的解形式设为x(t)=x0eλt, 则式(2)的特征方程为
在复数域内, 令λ=σ+iω, 代入式(3)并分离实部、虚部得
1+w+2ζσ+σ2-ω2-we-στcos(ωτ)=0, 2(ζ+σ)ω+we-στsin(ωτ)=0.
当σ>0时, 随t的增大x=x0e(σ±iω)t→∞, 系统(1)是不稳定的; 当σ<0时, 随t的增大x=x0e(σ±iω)t→0, 系统(1)是稳定的; 当σ=0时,x=x0e(σ±iω)t被定义为系统(1)的稳定临界点, 即可能发生Hopf分岔的位置.为了找到该临界点, 可令式(3)中的σ=0, 得到复特征方程为
将式(4)分离实部与虚部得

设临界点为(σ,τ,ω)=(0,τc,ωc), 此时系统(1)发生Hopf分岔, 因为式(2)的两个复共轭特征根λ=σ±iω穿过虚轴.为了说明这种情况, 对式(3)做全微分, 可得λ关于τ的导数形式如下:
进而有
此时系统(1)发生Hopf分岔.由式(5)可求得
其中:w和ζ均为小于1的正的常数;k=1,2,3,….
2 再生型颤振系统的Hopf分岔类型判定
引入新变量Tn=εnt(n=0,1,…), 即T0=t,T1=εt,T2=ε2t, …,ε表示一个无量纲的小参数.其关于t的导数定义为
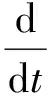
(9)
如果系统(1)的解含有慢尺度变量T1=εt, 则将在O(ε3)处出现永年项, 因此其解不应含有慢尺度变量, 所以其解可近似表示为

令
其中δ为调谐参数.将式(10),(11)代入式(1), 并比较方程两边ε,ε2和ε3的系数, 可得下列摄动方程:

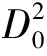
其中xi=xi(T0,T2);xiτ=xi(T0-τ,T2).式(12)的解可写为
将式(15)代入式(13), 解得

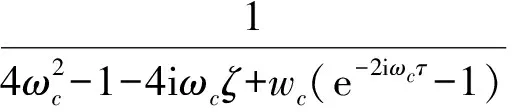
将式(15),(16)代入式(14), 为消除永年项, 令e±iωcτ的系数为零, 可得

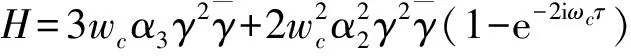
在复数域内, 令A(T2)=u(T2)+iv(T2), 则式(17)化为

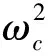

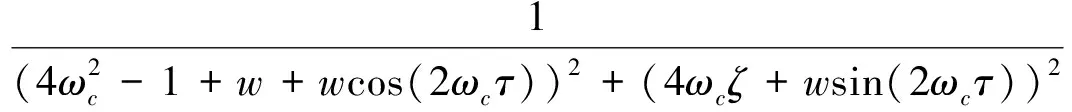

分离式(18)的实部、虚部得

其中h(u,v)和g(u,v)为不低于2次的非线性项, 表示如下:


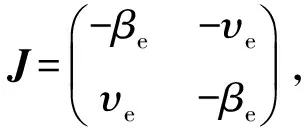
求得特征值为λ1,2=-βe±iυe.
当βe=0,υe≠0时, 式(22)存在一对纯虚根λ1,2=±iυe, 根据Hopf分岔定理, 此时系统发生Hopf分岔.由于βe和υe是时滞参数τ的函数, 因此调整时滞参数τ可控制Hopf分岔发生, 也将影响Hopf分岔方向和周期解的稳定性.应用Poincare-Birkhoff范式定理对系统(1)发生的Hopf分岔类型进行判断, 令
将式(20),(21)代入式(23)得

当βe=0,υe≠0时,δ≠0,Q≠0, 所以根据βe=-2Qδζq2,υe=2Qδζq1有q2=0,q1≠0, 则式(24)变为
当η<0时, 系统(1)发生超临界Hopf分岔, 产生稳定的极限环; 当η>0时, 系统(1)发生亚临界Hopf分岔, 产生不稳定的极限环.
3 数值仿真
针对系统(1), 取参数ζ=0.003 2,w=0.012,α2=1,α3=1,δ=1,ωc=2.011 6.当参数τ∈(0,3.908 8)时, 系统(1)稳定, 时间历程与相轨迹如图2所示, 此时τ=3.780 5; 当参数τ∈(3.908 9,3.910 5)时, 发生超临界Hopf分岔, 时间历程与相轨迹如图3所示, 此时τ=3.908 9,η=-0.036 6; 当τ∈(3.910 6,5.468 4)时, 系统发生亚临界Hopf分岔, 时间历程与相轨迹如图4所示, 此时τ=4.778 7,η=1.117 3; 当τ∈(5.468 5,5.469 4)时, 系统再次发生超临界Hopf分岔(图略); 当参数τ>5.469 4时系统稳定.
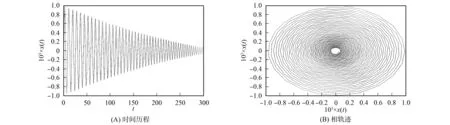
图2 当τ=3.780 5时稳定系统的运动情况Fig.2 Motion state of stable system for τ=3.780 5

图3 当τ=3.908 9时发生超临界Hopf分岔系统的运动情况Fig.3 Movement of system with supercritical Hopf bifurcation for τ=3.908 9
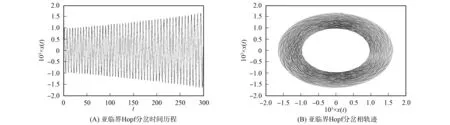
图4 当τ=4.778 7时发生亚临界Hopf分岔系统的运动情况Fig.4 Movement of system with subcritical Hopf bifurcation for τ=4.778 7
随着参数的变化, 系统(1)会先由稳定到发生超临界Hopf分岔, 再发生亚临界Hopf分岔, 然后再在某个参数的邻域内发生超临界Hopf分岔, 最后当参数大于该参数的邻域时系统渐近稳定.实际上, 如果系统(1)发生Hopf分岔, 则会使系统失去稳定性, 即刀具器械在实际工作过程中将遭受严重损坏.下面主要针对τ∈(0,10)区域, 为系统(1)设计合理、有效的控制器, 避免系统发生Hopf分岔.
4 再生型颤振系统的分岔控制
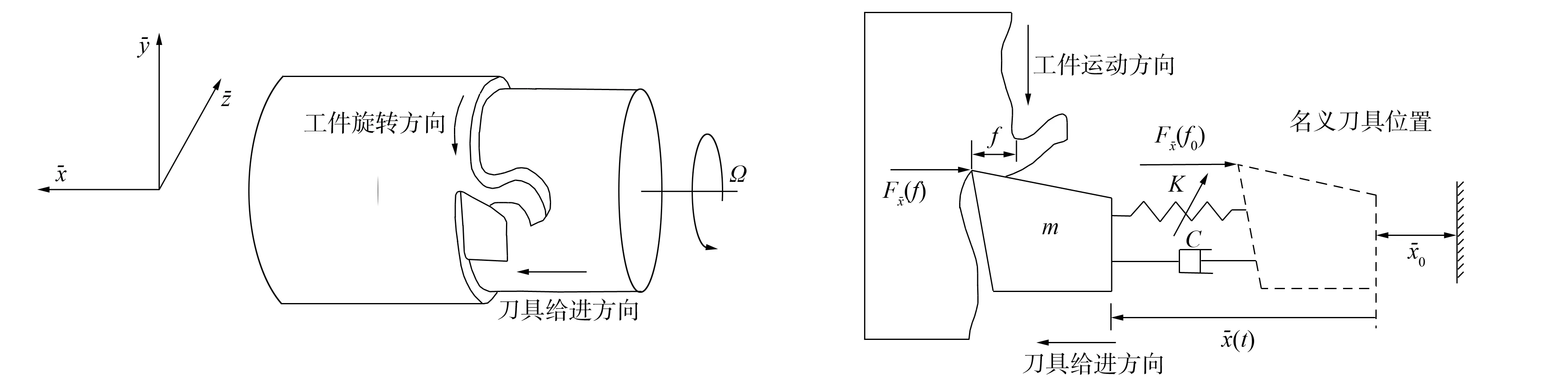
图5 刀具振动模型Fig.5 Tool vibration models
刀具及其刀具固定器可近似简化为一个单自由度的弹簧系统, 其阻尼系数为C, 弹簧刚性系数为k, 刀具质量为m.实际的工件切削厚度可由下式给出:

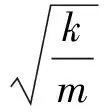

其中:μ表示切削宽度;M的大小与其切削参数有关, 如切削速度、刀具的几何形状和f0大小等.假设M和μ均为常数, 对式(28)关于f在f0处进行三阶Taylor展开并代入方程(27), 对其进行无量纲化得到具有位移反馈系统的运动方程为
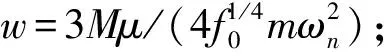

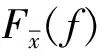
其中:xτ0=x(t-τ0),τ0<τ;α2,α3,a和k0为常数.
取参数ζ=0.003 2,w=0.012,α2=1,α3=1,k0=2.540 3×10-5,τ0=3.0,a=9.当参数τ∈(0,3.908 8)和τ>5.469 4时, 控制系统(31)稳定; 当参数τ∈(3.908 9,3.910 5)时, 原系统发生超临界Hopf分岔, 而通过数值仿真可验证控制系统(31)同样稳定, 原系统及控制系统的时间历程如图6所示, 此时τ=3.908 9; 当τ∈(3.910 6,5.468 4)时, 原系统发生亚临界Hopf分岔, 而通过数值仿真可验证控制系统(31)仍然稳定, 原系统及控制系统的时间历程如图7所示, 此时τ=4.778 7; 当τ∈(5.468 5,5.469 4)时, 原系统发生超临界Hopf分岔, 而通过数值仿真可验证控制系统(31)仍然稳定(图略).

图6 τ=3.908 9时临界Hopf分岔的控制Fig.6 Supercritical Hopf bifurcation control for τ=3.908 9
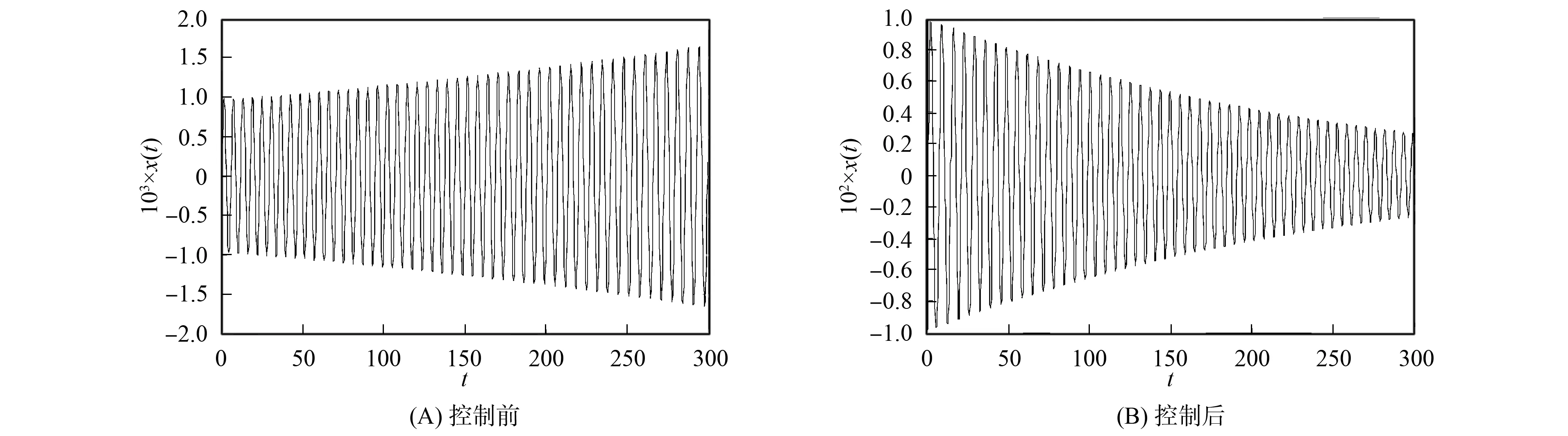
图7 τ=4.778 7时亚临界Hopf分岔的控制Fig.7 Subcritical Hopf bifurcation control for τ=4.778 7
综上所述, 本文针对再生切削颤振系统, 利用多尺度法结合Poincare-Birkhoff范式定理, 分析了系统的分岔特性, 并针对系统发生的Hopf分岔, 设计了非线性延迟控制器, 将原系统发生的亚临界Hopf分岔、超临界Hopf分岔均控制为稳定, 并通过数值模拟验证了所设计控制器的有效性.
[1]赵愿玲, 左曙光.考虑驱动力影响的轮胎侧向自激振动分析 [J].振动与冲击, 2012, 31(22): 101-105.(ZHAO Yuanling, ZUO Shuguang.Lateral Self-excited Vibration Analysis for a Type Considering Driving Force [J].Journal of Vibration and Shock, 2012, 31(22): 101-105.)
[2]贾尚帅, 丁千, 刘炜.超音速弹翼非线性颤振分析与控制 [J].振动与冲击, 2012, 31(13): 108-112.(JIA Shangshuai, DING Qian, LIU Wei.Nonlinear Flutter Analysis and Control of Supersonic Missile Wings [J].Journal of Vibration and Shock, 2012, 31(13): 108-112.)
[3]阳辉, 黄筱调, 方成刚.数控再生型切削颤振系统的分析及仿真 [J].机床与液压, 2009, 37(1): 35-37.(YANG Hui, HUANG Xiaodiao, FANG Chenggang.The Analysis and Simulation of NC Regenerative Cutting Chatter System [J].Machine Tool and Hydraulics, 2009, 37(1): 35-37.)
[4]刘习军, 王立刚, 贾启芬.一种由干摩擦引起的车床切削颤振 [J].工程力学, 2005, 22(1): 107-112.(LIU Xijun, WANG Ligang, JIA Qifen.Cutting Chatter of Machine Tools Induced by Dry Friction [J].Engineering Mechanics, 2005, 22(1): 107-112.)
[5]Pilkee Kim, Sanghyun Bae, Jongwon Seok.Bifucation Analysis on a Turning System with Large and State-Dependent Time Delay [J].Journal of Sound and Vibration, 2012, 331: 5562-5580.
[6]李鹏松, 陈书吉, 吕雪, 等.单参数电力系统亚临界Hopf分岔控制 [J].吉林大学学报: 理学版, 2013, 51(4): 618-622.(LI Pengsong, CHEN Shuji, LÜ Xue, et al.Subcritical Hopf Bifurcation Control of Power System with Single Parameter [J].Journal of Jilin University: Science Edition, 2013, 51(4): 618-622.)
[7]刘爽, 刘彬, 张业宽, 等.一类时滞非线性相对转动系统的Hopf分岔与周期解的稳定性 [J].物理学报, 2010, 59(1): 38-43.(LIU Shuang, LIU Bin, ZHANG Yekuan, et al.Hopf Bifurcation and Stability of Periodic Solutions in a Nonlinear Relative Rotation Dynamical System with Time Delay [J].Acta Physica Sinica, 2010, 59(1): 38-43.)
[8]陈衍茂, 刘济科.非线性颤振系统中既是超临界又是亚临界的Hopf分岔点研究 [J].应用数学和力学, 2008, 29(2): 181-187.(CHEN Yanmao, LIU Jike.Supercritical as Well as Subcritical Hopf Bifurcation in Nonlinear Flutter Systems [J].Applied Mathematics and Mechanics, 2008, 29(2): 181-187.)
[9]XIE Qizhi, ZHANG Qichang, HAN Jianxin.Hopf Bifurcation for Delay Differential Equation with Application to Machine Tool Chatter [J].Applied Mathematical Modelling, 2012, 36(8): 3803-3812.
[10]Faria T.Stability and Bifurcation for a Delayed Predator-Prey Model and the Effect of Diffusion [J].J Math Anal Appl, 2001, 254(2): 433-463.
[11]Hanna N H, Tobias S A.A Theory of Nonlinear Regenerative Chatter [J].J Manuf Sci Eng, 1974, 96(1): 247-255.
[12]陆启韶, 彭临平, 杨卓琴.常微分方程与动力系统 [M].北京: 北京航空航天大学出版社, 2010.(LU Qishao, PENG Linping, YANG Zhuoqin.Ordinary Differential Equations and Dynamical Systems [M].Beijing: Beihang University Press, 2010.)
AnalysisandControlofHopfBifurcationforRegenerativeChatterSystem
LI Pengsong, SHENG Guiquan, MENG Yongyong
(CollegeofSciences,NortheastDianliUniversity,Jilin132012,JilinProvince,China)
We considered a class of retarded one-degree-of-freedom nonlinear system, namely, the regenerative model of chatter in a lathe machine tool.The time-delay influence on the stability of the system solutions was analyzed with the aid of multiple scales.Nonlinear displacement feedback control can be used to suppress the self-sustained oscillation caused by Hopf bifurcation.The results of the theory analysis and numerical simulation show that the designed controller is valid for the cutting chatter system.
subcritical Hopf bifurcation; supercritical Hopf bifurcation; nonlinear control; method of multiple scales
2014-03-03.
李鹏松(1970—), 男, 汉族, 博士, 教授, 从事非线性动力系统的研究, E-mail: li-pengsong@163.com.
国家自然科学基金(批准号: 11072085)和吉林省科技发展计划项目(批准号: 20130101065JC).
O193
A
1671-5489(2014)06-1155-07
10.13413/j.cnki.jdxblxb.2014.06.09
赵立芹)

