基于多尺度样本熵的往复式压缩机故障诊断方法研究

田 智，朱 琴，练兴元，朱 涛，王 雪

(1.中石油西南油气田分公司川西北气矿，四川 江油 621700)(2.重庆科技学院 电气与信息工程学院，重庆 401331)

基于多尺度样本熵的往复式压缩机故障诊断方法研究

田 智1，朱 琴1，练兴元1，朱 涛1，王 雪2

(1.中石油西南油气田分公司川西北气矿，四川 江油 621700)(2.重庆科技学院 电气与信息工程学院，重庆 401331)

往复式压缩机工作时的振动信号非常复杂，对采样数据经过替代数据法和最大Lyapunov指数分析后发现具有一定的非线性和弱混沌性，这样的数据特征在其故障诊断时较适合采用样本熵(Sample Entropy，SampEn)进行处理。为实现往复式压缩机振动故障诊断，研究了振动信号符号化处理方法，提出了符号序列的SampEn算法，分析了不同时延参数下SampEn值曲线的几何特征，并利用该几何特征构建了故障的标准模板，通过该模板实现了故障诊断。实验证明，利用SampEn可以进行压缩机典型故障的诊断，该方法具有工程实用价值。

往复式压缩机；振动；样本熵；故障诊断

利用振动信号对往复式压缩机的故障进行诊断一直是学术界和工程界非常关注的问题。往复式压缩机结构复杂，工作时激振源众多，其振动信号既包含稳态周期信号，也包含周期冲击信号和随机冲击信号。其振动信号频谱往往非常复杂，很难直接利用频谱特征参数进行有效的故障诊断。

从机器的运行机理分析，机器系统在完全正常、初期故障、中期故障和严重故障以及发生不同的故障时，其系统的非线性动力学特征会发生变化。对于像往复式压缩机这样的多自由度非线性系统，从状态空间(相空间)角度很难建立起完备的非线性微分方程；但采用某些非线性动力学的统计参数进行故障诊断，却是一种有效实用的方法。目前该方法已引起了广泛的关注和重视[1-4]。

唐友福等人[5]采用均值符号化方法计算信号Lempel-Ziv复杂度(Lempel-Ziv complexity，LZC)，利用BP 人工神经网络对4种模拟故障的LZC特征分别进行训练和诊断，效果较好；Xin Jin等人[3]利用符号化数据，在小波变换的基础上，根据符号化数据后的非线性统计参数进行故障诊断和预测，效果较好；陈予恕[6]在研究12150发动机的监测技术时，采用了奇异谱分析方法，分析得出谱型变化对应机器的正常、不良和故障状态的结论，并认为奇异谱是不可建模的复杂机械系统故障诊断的重要指标；冯晓光[7]研究了近似熵(Approximate Entropy，ApEn)在往复式压缩机故障诊断上的应用，改进了熵算法，并应用到实际的工程项目中；苗刚[8]等人将多尺度Hilbert谱熵引入到高压聚乙烯装置的往复式压缩机组排气阀表面振动信号的分析中，分析了Hilbert谱熵的算法，比较了时频熵与多尺度Hilbert熵在实际应用中的效果，证实了多尺度Hilbert谱熵能更准确地反映机组的状态。

多尺度SampEn具有非常良好的特性，如要求样本少、允许数据缺损、状态稳定等特点，非常适合在现场对往复式压缩机进行故障诊断。本文利用振动时域信号进行多尺度SampEn故障诊断的研究，试图利用SampEn包含的丰富信息有效区分不同的往复式压缩机的故障。

1 往复式压缩机振动信号的动力学特征分析

要进行多尺度SampEn分析，首先需要研究往复式压缩机振动信号的特性，这些特性包括是否具有周期信号特征、是否非线性和是否具有混沌特性。

1.1振动信号的频谱分析

从引起往复式压缩机振动的激振源分析，主要有旋转惯性力、往复惯性力、气体周期冲击脉冲和摩擦力等。这些激振力使得压缩机得到的振动信号应该包含稳定的频谱值，同时由于非线性因素的存在，也会使得频谱变得复杂。图1和图2是中石油西南分公司川西北气矿江油雷三作业区3#往复式增压机采集得到的气缸盖轴向的振动信号。

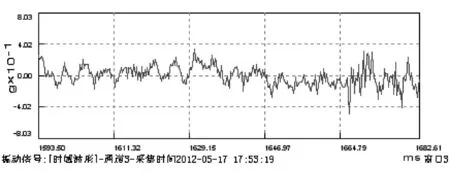
图1 压缩机气缸盖振动时域信号

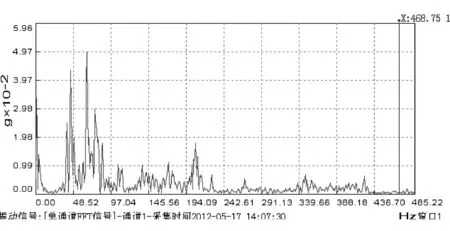
图2 压缩机气缸盖振动频域信号

尽管在频谱图里，惯性力引起的转频为频谱中的最大值，但频谱分布很广，在高频和低频区域还有较为复杂的成分。从频谱可以发现清晰的曲轴旋转转频及其倍频，因此该信号的周期性是显而易见的。

1.2振动信号的特性研究

对信号的非线性验证较为有效的方法是时间序列替代法[9]。首先对时间序列进行离散傅立叶变换(DFT)：

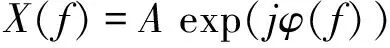
(1)

对傅立叶变化后的相位进行随机化处理，生成的新相位谱φ(f)∈[-π,π]。当信号长度为奇数时：

(2)

当信号长度为偶数时：

(3)

引入关联维判据：

(4)

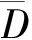
混沌情况的检测采用最大Lyapunov指数[10]。最大Lyapunov指数是混沌特性的一个重要指标，如果信号有最大Lyapunov指数且为正值，则说明该系统是混沌的。因实际获取的信号长度有限，故选用小数据量法[7]计算最大Lyapunov指数。

对信号进行相空间重构，计算相空间每个点的最短初始距离，并限制短暂分离。

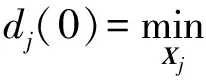
(5)

式中：Xi为相空间中的点；p为平均周期。对Xi，计算该邻点对的i个离散时间步长后的距离：

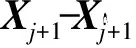
(6)

对每个i求出所有j的lgd(j)的平均值y(i):

(7)

式中：h为非零d(j)的数目。可以采用最小二乘法对曲线y(i)的直线部分做线性回归，直线的斜率就是最大Lyapunov指数λ1。

根据上面的算法，不同测点正常和气阀弹簧损坏两种情况的测试值见表1。

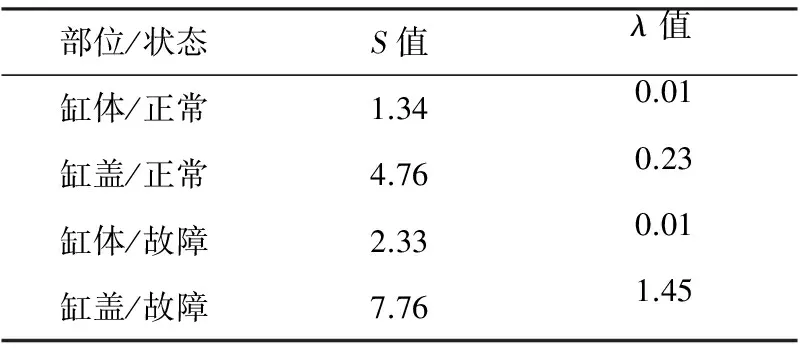
表1 正常和故障状态下的S,λ值

由上述分析可知，采集到的往复式压缩机的振动信号表现出线性和非线性动力学特征，可采用SampEn的方法进行故障诊断研究。

2 基于信号符号化条件下的多尺度样本熵算法

2.1SampEn算法

近似熵是Richman提出的一种时间序列复杂性测度方法[11]，它是在数据长度为N、相似容限为r、m点数据段模式相互相似的条件下，(m+1)点数据段模式相互相似的条件概率CP自然对数的近似值的负平均值。SampEn是CP严格的自然对数，它是近似熵的算法改进，降低了近似熵的误差。是一种精度更好的熵计算方法。

SampEn具有很多优点：(1)SampEn不包含自身数据段的比较，因此不依赖数据长度；(2)具有很好的一致性，在某个嵌入维m和容限r值下，某个序列的SampEn较另一个序列高，那么在其他的m和r下，该序列的SampEn值依然是高；(3)SampEn对数据丢失不敏感，适合工程上应用。

SampEn的算法如下：

步骤1：设{xi}为时间序列，将序列按照顺序组成m维矢量。

X(i)=[x(i),x(i+1),…,x(i+m-1)],i=1～N-m+1

(8)

步骤2：定义X(i)与X(j)之间的距离d[X(i),X(j)]为对应元素中差值最大值。

(9)

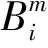
(10)

步骤4：将所有i的平均值记作Bm(r)。

(11)

步骤5：把维数加1，变成(m+1)，得到Bm+1(r)，重复步骤1～步骤4的过程。

步骤6：得到SampEn的理论值。

(12)

当样本为有限长度时：

(13)

一般情况下嵌入维为1～2，相似容限为数据样本标准差的0.10～0.25倍。

2.2基于符号化多尺度SampEn算法

实验分析表明，若直接采用上述公式(12)计算往复式压缩机上的振动时域信号，其对不同的故障分离效果不理想。为此提出如下解决思路：(1)对得到的振动信号进行符号化处理，也就是对原振动信号进行粗粒化处理，这一过程能够捕获大尺度的特征，从而降低动力学噪声和测量噪声的影响；(2)对符号化后的序列考虑时延尺度因子τ，分别形成τ=1,2,…,k时的子序列，对子序列按照SampEn进行计算，计算得到的SampEn曲线包含了不同工况的特征信息，可由此进行诊断。

在时间序列的值域范围内引入一个划分p=(p1,p2,…,pq)。将每个时域点的值放入划分中，于是每个点值将变成一个符号。考虑时延尺度因子τ，将符号序列生成不同尺度的子序列{Mj}:{Mj|Mi,i=0,kτ,2kτ,…,lkτ;k=1～N/2}。经过符号化处理后的时域信号如图3所示。

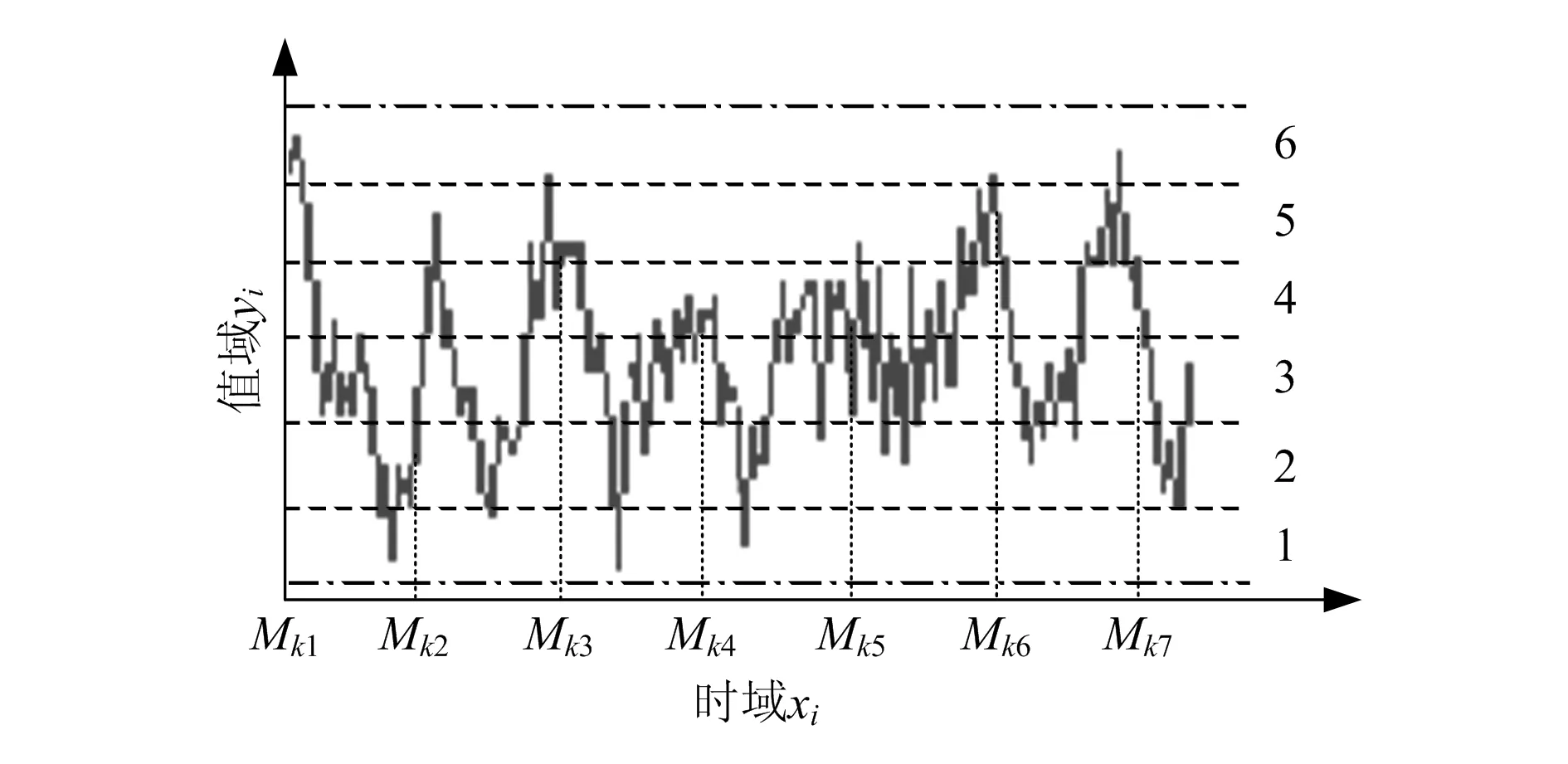
图3 时域信号进行符号化处理的结果

图3呈现的波形为图1中的时域信号(局部)经过符号化处理的情况。图中水平点划线表明值域范围，本文将该值域划分为6个部分，分别代表的值为1～6。图中{Mki}是时延尺度因子τ下的子序列。按照上面的分析，{Mki}可以表示为：

(14)

3 符号化多尺度SampEn的故障诊断

为采集不同状态下的往复压缩机振动试验数据，笔者依次在中石油西南分公司川西北矿区江油雷三工作站的1#工作机组的二级气缸上安装了正常、阀片断裂、弹簧损坏及阀片有缺口4种状态的气阀，进行故障模拟试验，转速为3 650r/min，加速度传感器布置在气阀的阀盖上，信号采集系统是自行设计开发的DPSS2010信号采集及故障诊断系统，采样频率为10 kHz，每种气阀状态各采集10 组数据样本，每组样本长度为240 000 个点。

为了更好地表征非线性参数的统计特性，对每种类型的工况采样组做如下处理：

步骤1：设置尺度因子τ=1。

步骤2：随机设置一个开始点M0作为子序列的起始点，设置子序列长度N=4 096，要求M0+4 096τ<240 000。

步骤3：在采样长度N=4 096上计算SampEn，得到Vτ=1值。

步骤4：对10组数据重复进行计算步骤2～3，对得到的10个Vτ=1值进行平均处理，作为τ=1的熵值。

步骤5：设置尺度因子τ=2，重复上述计算，得到Vτ=2的SampEn值。如此直到完成整个计算。得到的多尺度SampEn的值如图4所示。

图4 4种工况下的不同尺度因子的SampEn的值曲线

从图4可以看到，4种工况当中，多尺度SampEn曲线表现出的特性相同的部分：这些工况的SampEn值在时延很小时都较小，此时的嵌入维较小；在某个嵌入维的时候，SampEn值较为稳定，该稳定的SampEn值表征了不同故障的非线性动力学特征的程度。

4种不同的工况，对应的多尺度SampEn值的形状、均值、收敛值是不同的。尽管正常情况下和弹簧损坏时的故障状态曲线较为接近，但综合考虑形状、均值和收敛值，差异还是可以接受的。同时，由于数据是经过多次平均后的结果，具有较为稳定的统计特性。

在实际诊断中，用曲线的均值点、收敛点形成一个标准向量作为故障模板进行模板匹配就能很好地完成诊断。若采用数据驱动下的建模处理，如RBF神经网络、SVM等，还可以达到更好的诊断效果。

构建的标准模板为：

Di={Xi,Yi,Vi}

(15)

式中：Di为故障标准向量；Xi为曲线面积的重心横坐标；Yi为曲线面积的纵坐标；Vi为收敛值。本文利用方差条件定义该值，从某个时延点τt开始，若后面所有ApEn值点的方差小于某个指定值，就认为该点为收敛值的起始点，计算从该起始点到τ20的平均值即为收敛值。

在现场的实验中，利用本文方法对处于故障的1#机进行测试时发现，1#机缸盖的加速度振动信号的SampEn曲线得到的特征向量与阀片有缺口的标准模板特征向量的欧氏距离最短，因此判定为阀片缺口故障。经过现场的检验，证明诊断是正确的。

4 结束语

本文通过研究基于多尺度SampEn的往复式压缩机的故障诊断方法，得出如下结论：(1)从振动信号自身的特点分析，它具有一定水平的非线性动力学特征，因此采用SampEn熵描述是可行的。(2)对振动信号进行符号化处理后，进行SampEn计算，采用模板匹配方法可以区分不同故障。但目前该方法还存在一些问题，如正常状态和一些故障区分度不是十分理想，初期故障表现出来的多尺度SampEn比较接近，因此该方法还需要进一步完善。

[1] 姜波．往复式压缩机的振动分析研究[J]．山东理工大学学报，2009，23(5)：93-97．

[2] XIAO J，XU W，GU C G，et al．Self-recirculating casing treatment for a radial compressor[J]．Chinese Journal of Mechanical Engineering，2009，22(4)：567-573．

[3] Xin Jin，Shalabh Gupta， Kushal Mukherjee，et al．Wavelet-based feature extraction using probabilistic finite state automata for pattern classification[J]．Pattern Recognition，2011，44：1343-1356．

[4] 张来斌，陈敬龙，段礼祥．基于混沌理论的往复式压缩机故障诊断[J]．中国石油大学学报：自然科学版，2012，36(1)：112-115．

[5] 唐友福，刘树林，刘颖慧,等． 基于非线性复杂测度的往复压缩机故障诊断[J]．机械工程学报，2012，48(3)： 102-107．

[6] 陈予恕．机械故障诊断的非线性动力学原理[J]．机械工程学报，2007，43(1)：25-34．

[7] 冯晓光．近似熵在往复式压缩机故障诊断的研究应用[D]．大连：大连理工大学，2006．

[8] 苗刚．多尺度Hilbert熵谱在故障诊断中的应用[J]．农业机械学报，2006，38(3)：176-179．

[9] THEILER J，LINSAY P S，RUBIN D M．Detecting nonlinearity in data with long oherence time[C]// Time Series Prediction：Forecasting the Future and Understanding the Past. New York：Perseus Bocks Publishing，1993：29-455．

[10] MICHAEL T Rosenstein，JAMES J Collins，CARLO J De Luca．A practical method for calculating largest Lyapunov exponents from small data sets[J]．Physical D，1993，65： 117-134．

[11] Richman J S，Moorman J R． Physiological time-series analysis using approximate entropy and sample entropy[J]．American Journal of Physiology-Heart Circulatory Physiology，2000，278：2039-2049．

StudyonFaultDiagnosisMethodofReciprocatingCompressorsBasedonMulti-scaleSampleEntropy

TIAN Zhi1, ZHU Qin1, LIAN Xingyuan1, ZHU Tao1, WANG Xue2

(1.The Southwest Oil and Gas Company of Petro-China, Sichuan Jiangyou, 621700, China)(2. Chongqing Science and Technology University, Chongqing, 401331, China)

The vibration signals are very complex and nonlinear in the reciprocating compressor working process. Based on surrogated date method and max Lyapunov exponent method, it shows weak nonlinearity and chaos. Such data character in its fault diagnosis is more suitable for the sample entropy models. For the realization of the reciprocating compressor vibration fault diagnosis, it presents the method to transfer dynamic signals into symbolic sequence, proposes SampEn algorithm based on symbolic sequence and the geometry characters of SampEn value. Experiments show that the proposed method is a valid tool to distinguish different fault diagnosis of reciprocating compressors.

Reciprocating Compressors; Vibration; Sample Entropy; Default Diagnosis

10.3969/j.issn.2095-509X.2014.03.021

2013-12-25

田智(1981—)，男，四川南充人，中石油西南油气田分公司川西北气矿工程师，主要从事天然气开采及管理工作。

TU17

A

2095-509X(2014)03-0078-05