基于工艺要求的伺服压机行程曲线优化

王 俊，李 明

(上海大学 机电工程及自动化学院，上海 200072)

基于工艺要求的伺服压机行程曲线优化

王 俊，李 明

(上海大学 机电工程及自动化学院，上海 200072)

分析了伺服压机受冲压工艺约束存在弊病的原因，对基于冲压工艺的伺服电机驱动及其优化方法进行了研究，尝试选用各类曲线去修正并作对比。研究表明：运用样条曲线修正，可使工艺曲线光滑、平整并保证衔接完美过渡，避免了瑕疵，有效地提高了冲压过程的动态特性。

伺服压机；运动仿真；行程曲线；线性优化

伺服压机是以伺服电机为主动力，由计算机控制的一种智能化、柔性化新型压机，由于取消了飞轮、离合器、制动器等部件，不仅克服了传统压力机运动特性单一、工艺适用性差、行程无法调整的固有缺陷，还大大提高了工作性能、运行精度，降低了能耗、磨损，延长了磨具寿命。但在冲压工艺要求较高的场合，由于工艺曲线是由多条运动曲线拼接而成，滑块在曲线拼接位置存在冲击震动现象[1]。为尽可能保证位移、速度、加速度曲线的平稳，降低噪声，需要对工艺行程曲线进行修正。

1 伺服压机传动系统分析

1.1伺服压机工作原理

图1为一种伺服压机的连杆和滑块运动部分简图，其通过永磁交流伺服电机带动齿轮减速，驱动曲柄肘杆机构，获得滑块的直线运动，所以通过控制伺服电机，就能实现滑块运动特性曲线的可调和压力的可控。而控制电机的核心在于控制曲线，

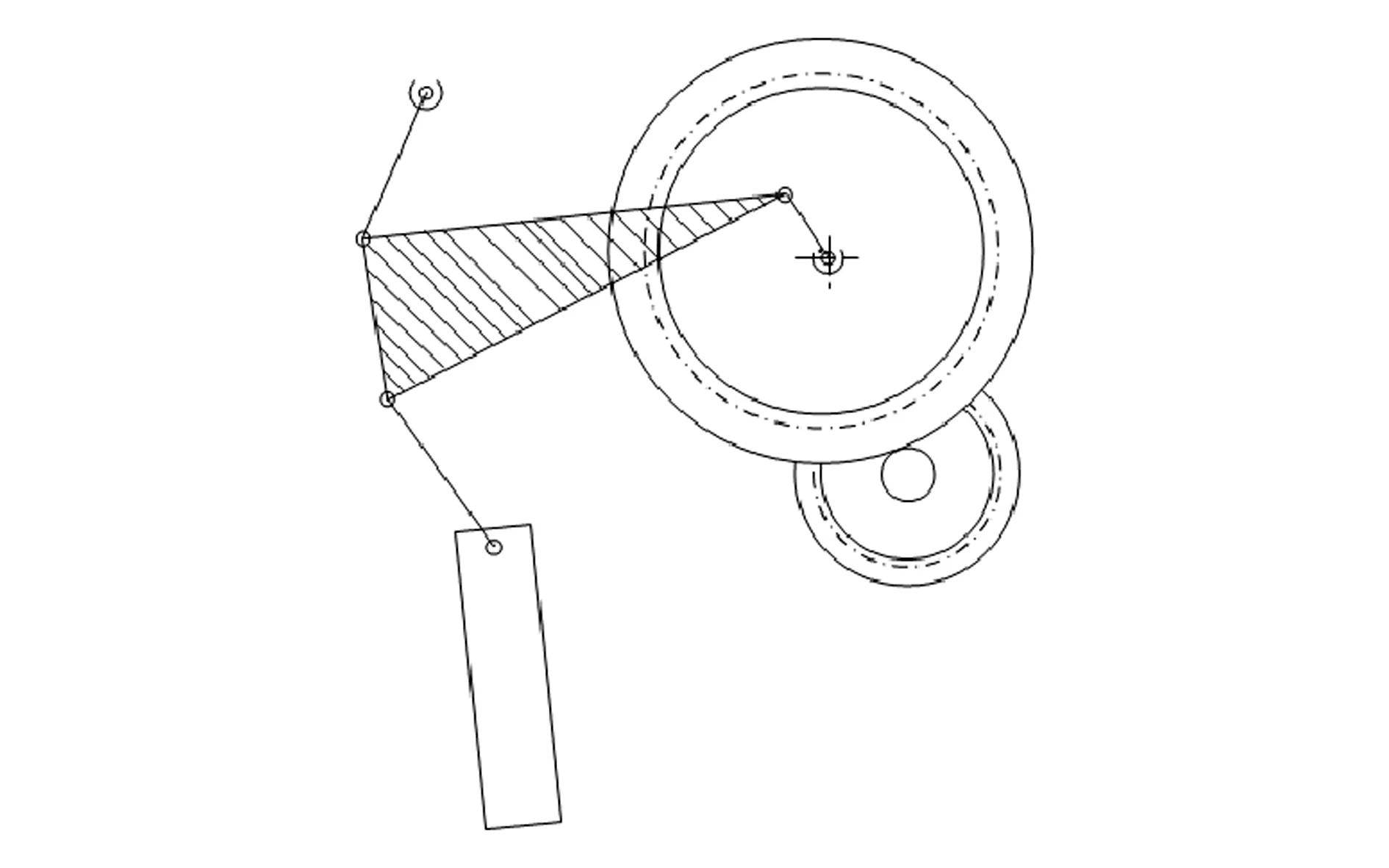
图1 连杆和滑块运动部分简图

对压机而言，该曲线受到相应的冲压工艺约束。

1.2压机运动机构建模与分析

如图2所示，以O为原点建立直角坐标系，其中MA为曲柄，长度设为a；AB为三角连杆的一条直角边，长度设为b；NB为摇杆，长度设为c；M点为凸心轮转轴中心，OM长度设为d；N点为摇杆固定在立板上的转轴中心，ON长度设为e；BC为三角连杆另一条直角边，长度设为f；CS为连杆，长度设为g；1 180mm是滑块(滑柱)的长度，S点是其上顶点；H为滑块底面到工作平台的高度，其范围为0～200mm；θ是凸心轮[2]相对于水平线的转角；β是摇杆相对于竖直线的夹角。

图2 伺服压机传动系统简化结构

H-θ公式的推导：此模型所涉及的自由度、运动不唯一性较多，采用常规的方法计算繁琐复杂。因而利用坐标法、向量间关系、距离公式可得A点坐标为(d+a·cosθ,a·sinθ)；B点坐标为(c·sinβ,e-c·cosβ)；C点坐标为(XC，YC)。

由A，B，C点坐标及BA·BC=0的关系可推得以下关系式：

(c·sinβ-d-a·cosθ)2+(a·sinθ+c·cosβ-e)2=b2

(YC-e+c·cosβ)2+(XC-c·sinβ)2=f2

(1)

进而推导出C点坐标：

最后推导出滑块行程的函数通式：

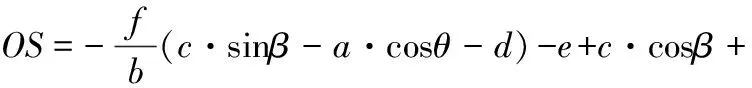
H=468-OS

(2)

式中包含了上文提到的两个自变量参数θ,β，在分析时应将式(1)、式(2)相结合。

2 基于Inventor数字样机的建模与分析

2.1三维模型构建

根据相关结构参数构建的CAD模型如图3所示，其中一级减速机构(与偏心轮相连接的皮带轮)和伺服电机未画出，因为其与转轴的输入存在简单的转速比关系，并不影响后续的分析研究。

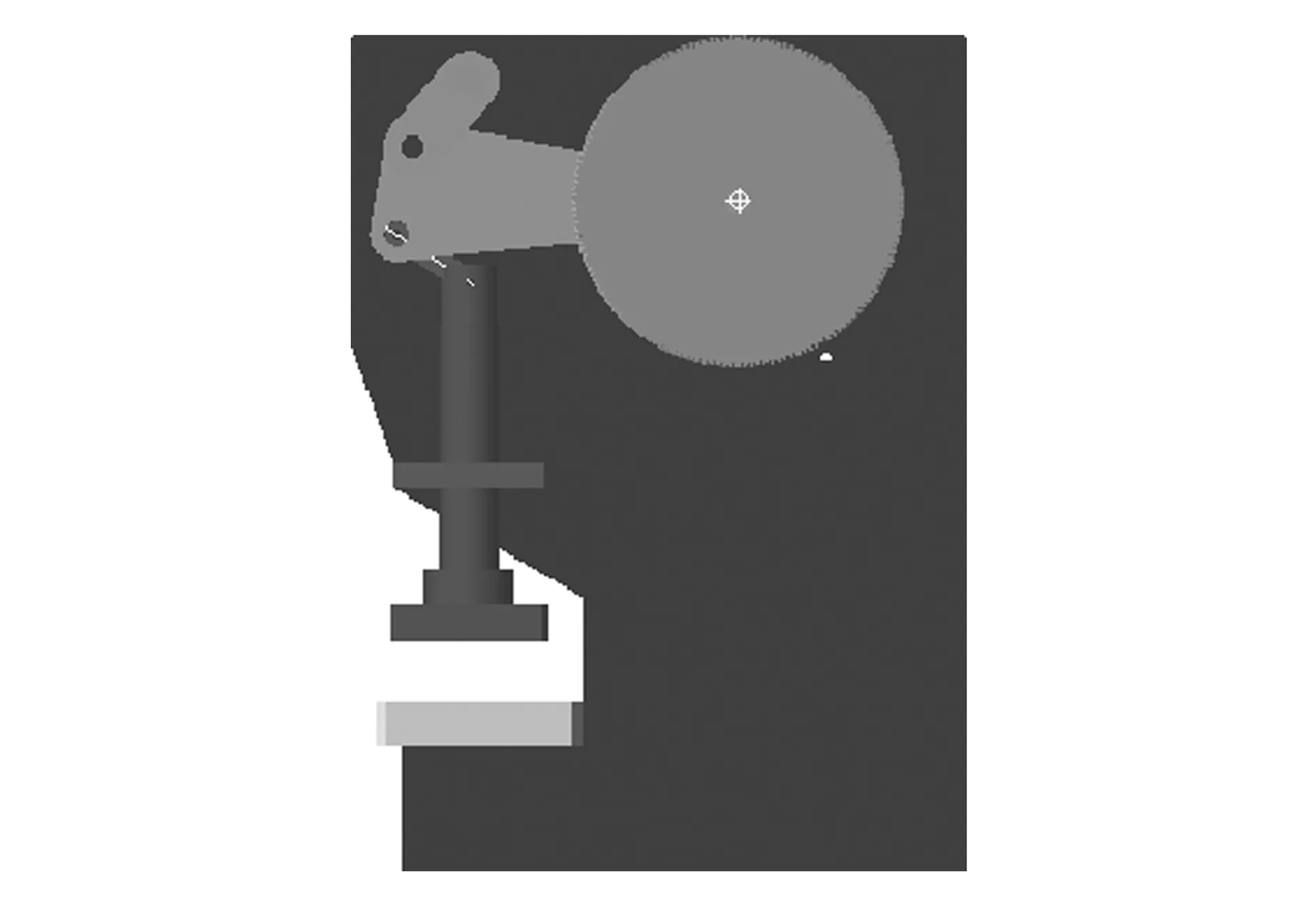
图3 伺服压机建模

2.2仿真模拟与分析

在虚拟的环境中进行运动学仿真分析，可以了解预设工艺曲线的实际运动学性能，同时还能检验模型建立的正确性。

3 基于线性优化的运动控制分析

3.1典型工艺曲线及分析优化

如图4所示，曲线①是所有优化曲线的原型，即工艺要求。机构的偏心轮在转到180°附近时，滑块处在最低点，然后上升返回。由于采用了多段曲线的简单拼接，因此在拼接部分就会出现相应的运动冲击，比如偏心轮旋转到0°、180°、360°等一些特殊点位置时,尤其容易出现瑕疵、噪声，本文针对这些问题进行优化。

图4 典型工艺曲线

图5为运用Inventor软件运动学分析功能得到的偏心轮速度和加速度曲线：曲线①是偏心轮速度曲线，可见电机的转速在滑块行程的起点和终点附近有一定的波动，中间段较平缓；曲线②是其加速度曲线，除了有明显的波动幅度外，在某些位置出现了波折。显然，所有曲线拼接处的瑕疵会对电机造成震荡，严重影响设备的工作性能。

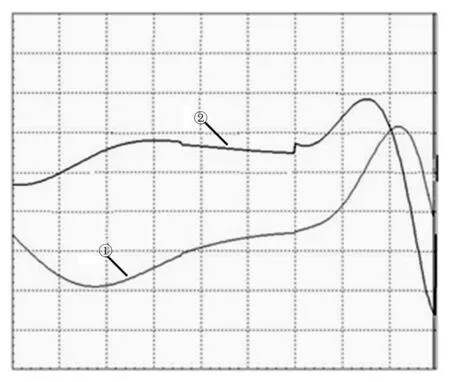
图5 偏心轮速度及加速度曲线

优化的具体步骤：

首先，鉴于典型工艺曲线的形状已经确定，需找到局部瑕疵的位置。

其次，输入不同类型的曲线拼接完整，查看偏心轮速度、加速度即输出曲线的情况。

最后，反复对比，取最理想值。

经过三次方曲线修正后，从对应的速度、加速度曲线图就可直观形象地看出两者呈波浪形与直角锯齿形，且波动幅度很大。经摆线修正后的图像对比之前的曲线图可得：其速度图谱的波形更陡，虽然波峰与波谷交替出现较为完整，但波动依旧巨大；加速度方面略有好转，但总体情况依旧很糟。同时，从中也发现一个规律，输出曲线的波动幅度、平缓程度的变化趋势与输入的修正曲线变化情况相一致，即两者成正反馈的关系[3-4]，这点从之后谐波、修正正弦、修正梯形曲线的替代检验中也得到印证。

为使优化效果更为明显，选择能自拟定参数数值的曲线，比如正弦、多项式,但因输入的凸轮转角曲线的数值随时间增加而增大，正弦曲线的变化趋势与其不一致，也被排除。换用多项式曲线，其n次项前面的常系数设置比较困难，稍有误差就会造成对应的输出曲线衔接点过渡不均匀、中间段曲率变化过快,其缺陷与之前实验过的曲线是一样的，但可以取得一定的优化效果。

综上所述，修正曲线必须满足：

a.能提供设计者自拟定的数据变量，数量合理。

b.波动幅度较小，曲率变化慢，且变动范围微小。

c.衔接点过渡平缓，弧度变化均匀。

因此，选择同时符合上述条件的曲线——样条曲线，用以修补拼接处的瑕疵。

运用样条曲线修正后的结果如图6所示(鉴于能使读者更明显看清优化后的数值变化，已将此图包括后文所有的图表放大了一定的倍数)，显然无论是速度还是加速度线条几乎平整光滑，之前的缺陷得到了很大的改善。

需要说明的是：

a.曲线①在0.667s时速度的突变是不可避免的，它是滑块行程与回程的交界点，是因为滑块在工作区间慢速冲压，而非工作区间快速收回所形成的，速度在265～600deg/s，也完全在额定的转速范围内。

b.加速度曲线②的最值偏差仅为0.5mm/s2,

图6 样条曲线修正后结果

具体数值也很微小，由此对电机产生的冲击、震动是微乎其微的，达到了优化的目的。

在筛选样条种类的时候，对不同类型样条曲线[5]的曲率及半径、比例因子、拐点和峰值点进行了比较，最终确定为三次B样条。原因在于：

a.其更容易弯曲变形。

b.曲线更接近它们的极点。

c.在后续的操作中执行效率更高(如加工、显示等)。

其分量形式如下：

式中：(x0，y0)，(x1，y1)，(x2，y2)，(x3，y3)为4个限制点；时间t取值为0～1s。

3.2原始曲线的截选分段

将线性优化后的典型工艺曲线细分成区间更多的几段基本曲线，为后续的拼接组合做准备，根据实际工况要求与开发自由编程的需要，将区间分为6段：[0°,120°]、[0°,170°]、[0°,180°]、[90°,170°]、[120°,180°]、[180°,360°]。

3.3任意组合后的自由编程

按照技术要求，伺服压机除能完成基本的动作外，扩展功能中另有几套可调节的工艺程序要求： (1)慢速下降、快速上升；(2)进行部分反转；(3)在上限停止1s。

扩展工艺曲线如图7所示。

针对这3种要求，同理按照之前的优化[6]方法选用三次B样条曲线，对端点拼接处进行弥补衔接，达到了同样理想的效果。

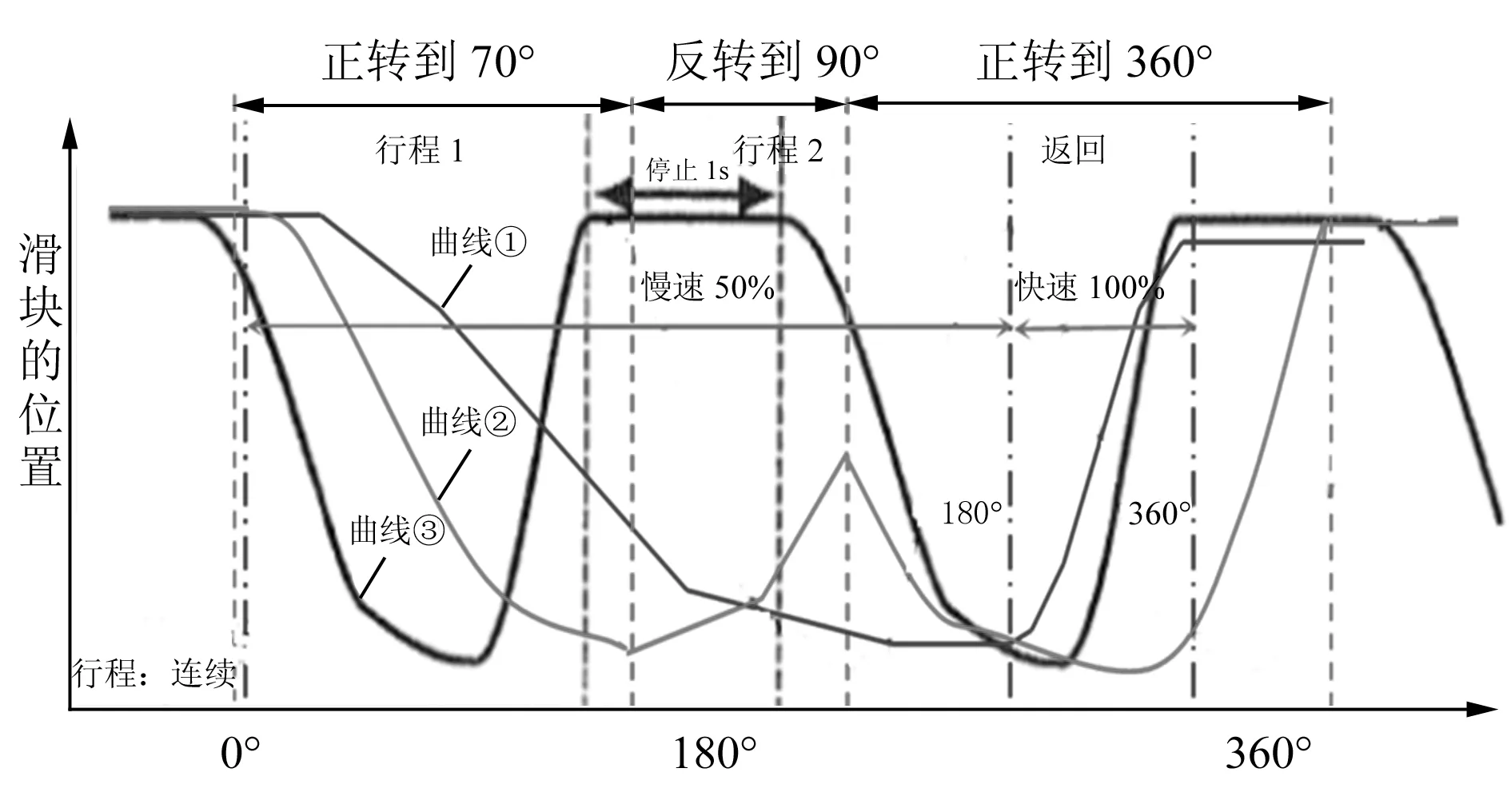
图7 扩展工艺曲线

针对要求(1)，为了使冲压行程的滑块速度是回程的一半，通过调试输入曲线的前后斜度获得了如图8所示的结果：曲线②是偏心轮速度曲线，前半段转速为262deg/s，后半段为524deg/s,且曲线依旧平滑光整。曲线①是对应的滑块行程曲线，其形状与典型的工艺曲线近似，偏差不大。

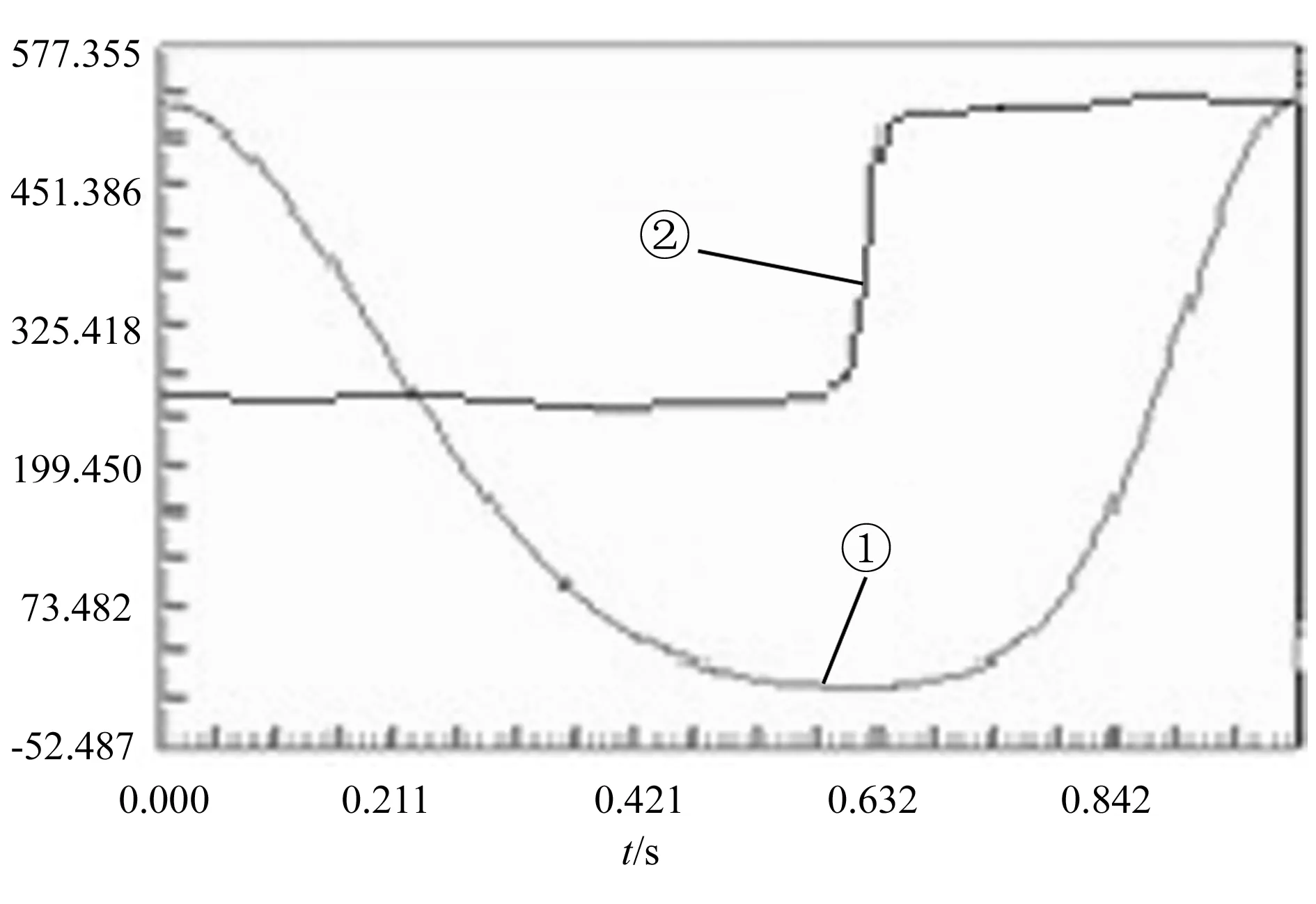
图8 要求(1)优化后结果

针对要求(2)，为实现部分反转，选择区间段[0°,170°]、[90°,170°]组合拼接在一起，端点的连接处依旧选择样条曲线过渡。由于工艺要求偏心轮转到170°时，先回转至90°处，然后再按照从90°～360°正常运转，因此需要优化170°折返点处的偏心轮转角曲线，结果如图9所示：输入的偏心轮转角曲线关于折返点近似对称。

图9 要求(2)中偏心轮转角曲线

对应的偏心轮速度、加速度曲线如图10所示：曲线①表示对应的速度，显然优化得很平坦，某一瞬间突变是电机转向改变的交界点，是不可避免的；曲线②是加速度的局部放大图，其最值范围已被压缩到0.1deg/s2以内，基本符合工艺标准。

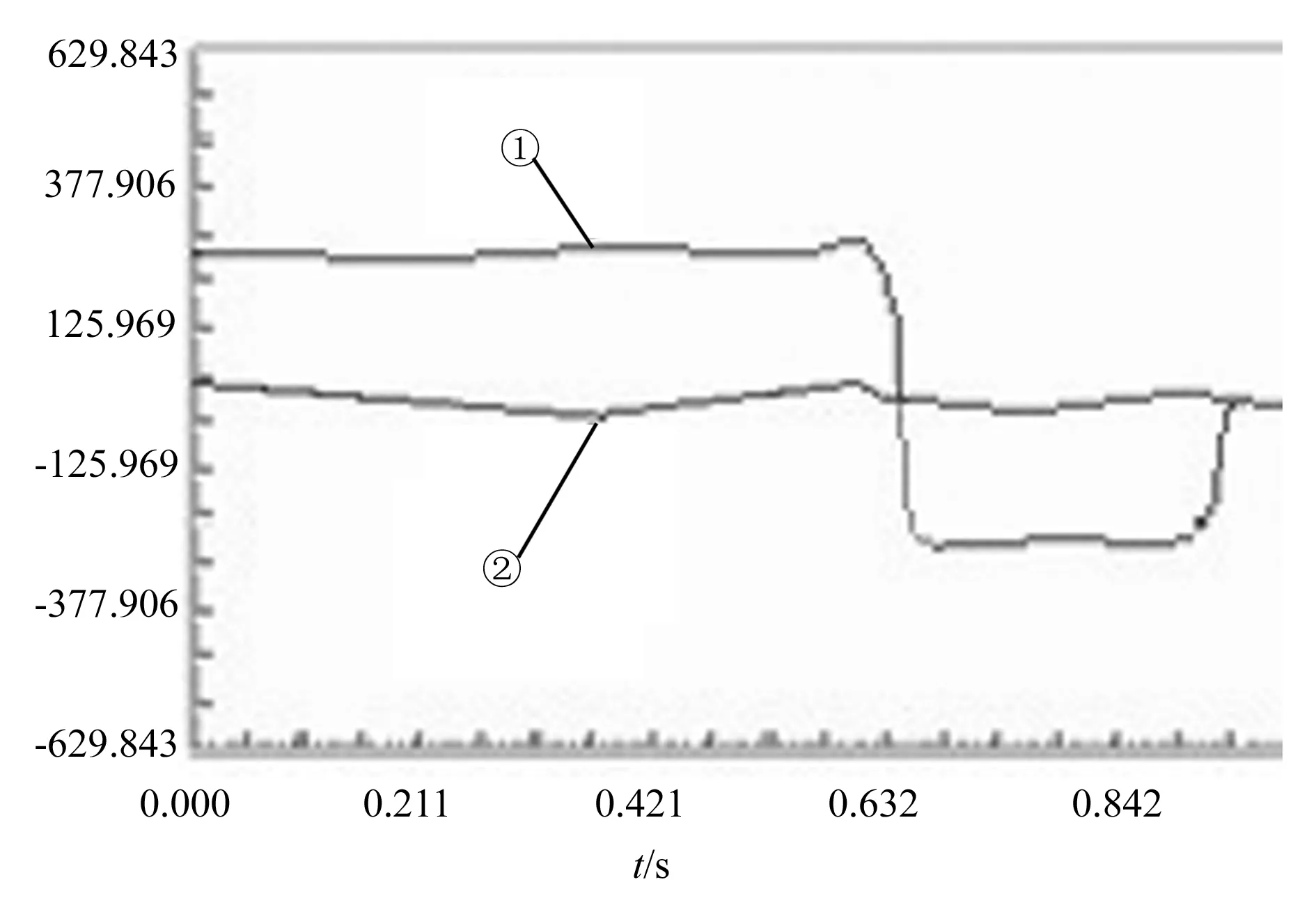
图10 要求(2)优化后结果

针对要求(3)，需要在上限停止1s。这表明滑块在完成一次冲压周期后，电机会停转1s，然后再进行下一个周期的运转。任务在于时间点1s处的合理连接，根据前面的经验，依旧选择样条曲线来连接，曲线与水平线间的空缺处演变成一个曲率较大的圆弧，如图11所示。

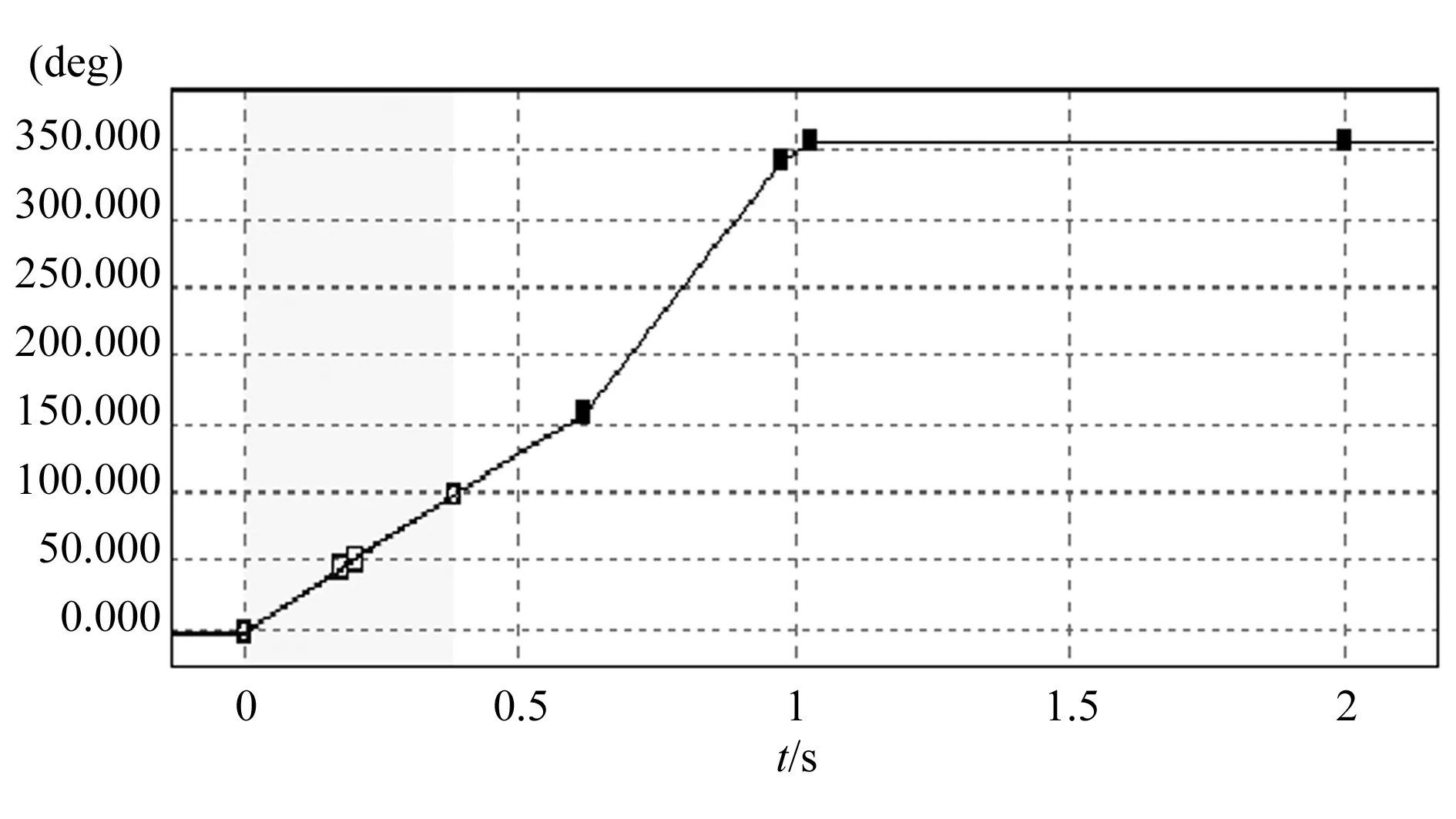
图11 要求(3)优化后结果

4 结束语

经过在Inventor运动仿真环境里的实验分析，在尝试了样条后发现，其在基本确保工艺精确度的前提下最接近优化目标，进一步研究表明：采用三次B样条修正典型工艺曲线，能有效地降低波动幅度，削减曲率突变，改善线性，保持曲线的平坦缓和；利用其衔接组合，曲线拼接处的端点可以保证良好的弧线过渡、均匀变化、减少拐点瑕疵，从而最大程度消除设备的噪声、震动与冲击。或许还存在其他种类的曲线，亦或是更为优越的样条类型，但本文所总结归纳的方法和探究思路已取得理想的效果，同时为相关领域的拓展提供了良好的借鉴。

[1] 韦佳. 浅析伺服压机对冲压工艺性的影响[J]. 模具制造, 2012 (5): 26-28.

[2] 石永刚，吴央芳.凸轮机构设计与应用创新[M].北京: 机械工业出版社,2007.

[3] 陈宝林.最优化理论与算法[M]. 北京: 清华大学出版社, 1989.

[4] 谢政, 李建平, 陈挚. 非线性最优化理论与方法[M]. 北京: 高等教育出版社, 2010.

[5] 崔锦泰, 程正兴.多元样条理论及应用[M].西安: 西安交通大学出版社, 1991.

[6] 范晋伟, 刘磊, 朱晓勇, 等. 伺服系统动态仿真及优化方法的研究[J]. 机械设计与制造, 2009 (1): 193-195.

TheOptimizationofServoPressStrokeCurveBasedonProcessRequirements

WANG Jun, LI Ming

(Shanghai University, Shanghai, 200072, China)

Based on the analysis of the causes of the stamping process defects in the servo press, it decomposes the process curve such as multiple splicing motion curve, slider and the position of the curve splicing error, vibration and shock phenomena. It studies the servo stamping process based on motor driving and optimization method, describes the selection of various types from comparison, obtains the motor speed, acceleration curves. This method can make the curves smooth, flat, and ensure the convergence perfect transition, avoid the defects, effectively improve the dynamic characteristics of stamping process.

Servo Press; Motion Simulation; Stroke Curve; Linear Optimization

10.3969/j.issn.2095-509X.2014.03.003

2013-12-27

王俊(1990—)，男，上海人，上海大学硕士研究生，主要研究方向为机械设计及制造。

TP215；TH133.5

A

2095-509X(2014)03-0010-05