补偿台偏心轮机构特性研究及优化

尹海鹏 ，石志孝 ，金雅融

（1.甘肃工大舞台技术工程有限公司，甘肃 兰州 730050；2.兰州理工大学机电工程学院，甘肃 兰州 730050；3.甘肃演艺装备工程研究中心，甘肃 兰州 730050）

0 引言

补偿台广泛应用于常规剧场和室外秀场，主要用于补平演出台面、运载车台、协助完成场景转换等功能[1]，也是演出时使用最频繁的台下安全设备之一。补偿台传动形式主要有螺旋顶升式、剪刀撑式、柔性升降柱式和偏心轮式，上述传动形式各有优缺点，其对使用条件的限制也各不相同。偏心轮机构因其结构紧凑、制造简单、成本较低等特点在行程较小的补偿台传动方案中被广泛应用。

偏心轮机构从动件的运动规律反应诸多信息，如从动件行程、机构运行平稳性、偏心轮的轮廓曲线等，所以解析运动学规律显得尤为重要。王东菱[2]、李雪军[3]考虑偏心轮周期性运动特点，采用有限傅里叶级数解析偏心轮从动件运动规律，获得无刚、柔性冲击偏心轮机构；吴孟丽[4]利用五次多项式解析运动规律并修正，设计出无冲击偏心轮机构；王薪鉴[5]基于B样条函数设计高速运动偏心轮从动件的运动规律，明显降低了偏心轮机构正弦规律运动时的最大运行加速度和噪声，韩炬[6]利用Creo Parametric机构模块的轨迹曲线功能构造偏心轮的轮廓曲线。诸多学者也注重偏心轮轮廓的优化，陈子侠[7]基于有限元分析并优化了偏心轮定子，有效降低了电机的摩擦力和内泄漏；安磊[8]通过动力学分析改善高速开盒机偏心轮机构运行平稳性；沈浩[9]通过在渐开线-圆弧曲线中插入高阶曲线的方法优化偏心轮泵转子，有效提高了偏心轮泵的输出介质的平均速度。

本文以演艺装备工程领域补偿台的偏心轮机构为研究对象，考虑补偿台的功能特点，将偏心轮设计为偏心轮机构。首先分析从动承载轮的运动规律[10,11]获得承载轮和偏心轮的最大接触力，并以此位置的结构参数建立优化模型，获得偏心轮结构参数的最优Pareto解集，通过应力检查动力学特性[12,13]进一步论证优化结果的合理性。

1 运动分析

补偿台偏心轮机构示意简图如图1所示，其中，Rb为偏心轮基圆半径，R为偏心轮半径，r为承载轮半径、s为承载轮位移、θ为任意时刻偏心轮的角位移，ω为偏心轮角速度，α为偏心轮机构的压力角，Re为偏心距，n-t为过接触点的正交系。易知，偏心轮与承载轮中心距。ΔOMA和ΔOMB中由相等列式可得压力角与偏心轮角位移的关系：

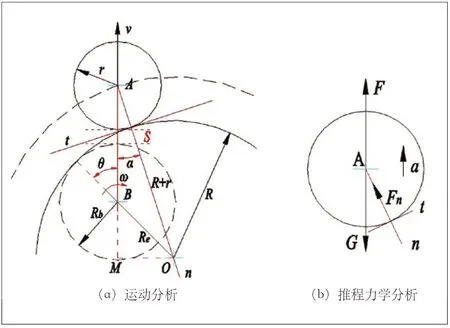
图1 偏心轮机构运动示意简图

式中，θ(t)为偏向轮不同时刻时的角位移，由式（1）得压力角

运动周期的任意时刻，偏心轮推力下承载轮的位移可表达为：

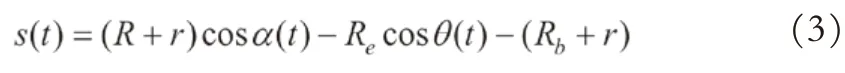
对位移求导，可得承重轮的速度：

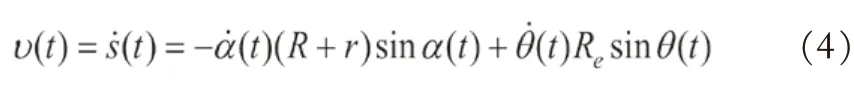
式中，

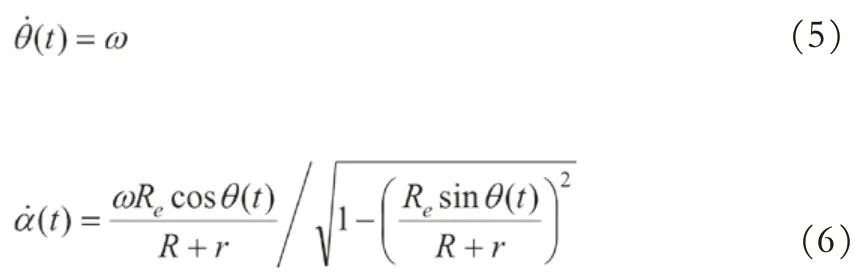
联立式（1）、式（5）、式（6）带入式（4），化简得承载轮任意时刻的升降速度：

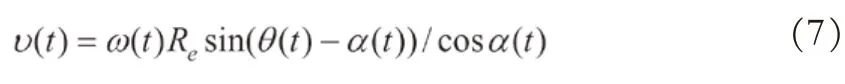
对式（7）求导可得承重轮任意时刻承载轮的运动加速度：

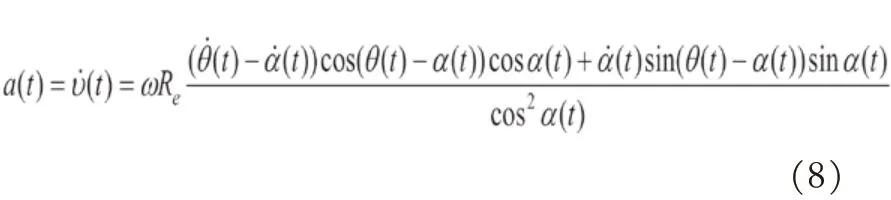
化简整理得：

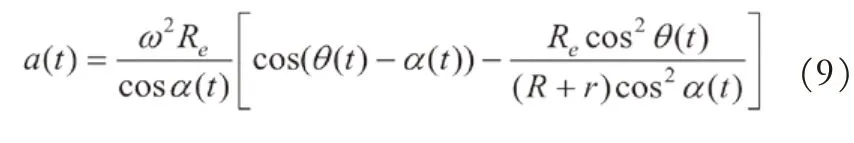
任意时刻承重轮起升推力或下降阻力可表达为：

式中，“＋”表示推程，“-”表示回程，M为补偿台最恶劣工况下折算到承重轮上的等效质量，取M=5 500 kg整理得：

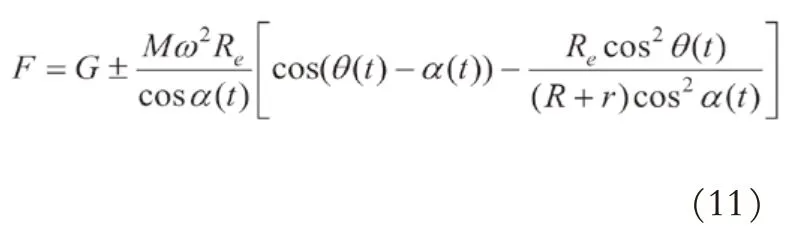
任意时刻承重轮和偏心轮接触正压力可表达为：

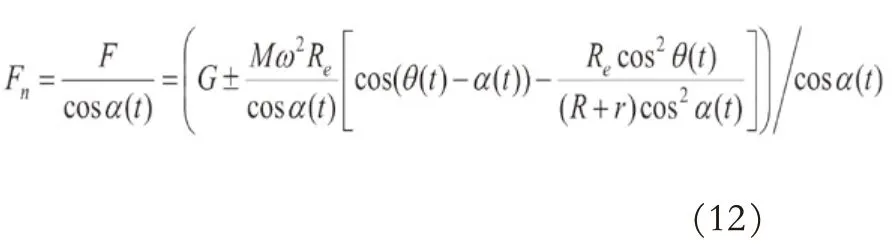
设计中，取Re=115.5 mm，Rb=84.5 mm，r=61.5 mm，R=200 mm，rad/s，并设起升方向为运动正方向，考虑到补偿台的运动特点，只解析偏心轮机构推程运动时的承重轮的运动规律，如图2所示。由“θ-α”曲线分析可知，推程运动偏心轮角位移θ(t)=90°时偏心轮机构的压力角最大为αmax＝±26.21°，此位置偏心轮机构的传动效率最低。从“θ-υ”曲线分析可知，承重轮在偏心轮角位移θ(t)=110°时获得最大速度υmax＝256.51 mm/s。从“θ-a”曲线分析可知，推程时承重轮先做加速度增大的加速运动，后做加速度减小的加速运动，最后做加速反向持续增大的减速运动到达推程最高点，在偏心轮运动起始、结束位置所需加速度a＝±264.91 mm/s2，在角位移θ(t)=180°时运行加速度最大amax＝684.05 mm/s2。由于补偿台在运动周期内运动不连续，承重轮在推程和回程内的起始、结束时速度为0、加速度均不为0，故该偏心轮机构虽无刚性冲击，但存在柔性冲击，优化偏心轮轮廓曲线并获得性能更好的组合运动规律是本课题下一步研究内容。

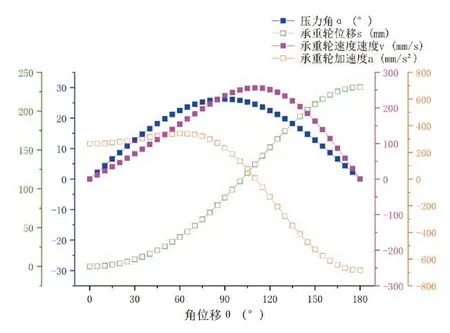
图2 偏心轮机构承重轮的运动规律

考虑补偿台台面p＝550 kg/m2的平均载荷以及车台和侧车台的随机载荷，折算到每套偏心轮机构上的等效载荷G=55 kN以此参数解析偏心轮机构的力学特性。由“θ-F”曲线分析可知，运动周期内，在偏心轮角位移角位移θ(t)=60°时，承重轮受最大起升力Fmax=56.88 kN。由“θ-Fn”曲线分析可知，运动周期内偏心轮和承重轮的最大法向接触力发生在偏心轮角位移处，其最大值为Fnmax=62.91 kN推程、回程运动中所需最大功耗近似，发生在偏心轮角位移分别为θ(t)=110°处，需要电机功率约为Pmax＝±14.12 kW（不考虑传动损失），其中“＋”表示释放功率，“-”表示吸收功率。考虑到一个运动周期T内，补偿台运动并不连续，即实际应用中，当t＝T／2时，补偿台运行至最大位移处停车并参与演出，根据力平衡条件，此时有F＝G，但理论解析值并不相等，这是因为起始、停车、结束位置处的加速度均不为0，此结论也很好地解释了起始、停车、结束位置处存在的冲击和振动。

图3 偏心轮机构力学特性分析

2 优化分析

实践中，承重轮采用45钢，为便于成型并取得较好的抗振性，偏心轮采用ZG310-570，其材料参数如表1所示。按上文设计中给定的结构尺寸进行静力学分析发现强度、刚度富裕，材料浪费严重，并给安装过程带来不便。针对这些问题，本节以质量最小为目标进行多目标优化[14]，寻求设计参数的最优组合。

表1 材料属性参数设置

2.1 优化数学模型

偏心轮可灵活设计的参变量如图4所示，考虑优化参数应用方便，优化变量设计为离散变量。其中，R1为开孔位置中心半径、D1为开孔直径、D2为偏心轮切除部分直径、t1为偏心轮厚度、t2偏心轮切除部分厚度，建立优化模型时考虑设计参数对称性，状态变量为局部最大等效应力σ(x)和局部最大总变形d(x)，目标函数为m(x)min。上述优化过程可描述为：寻求满足给定约束条件的参数组合[R1，D1，D2，t1，t2]，使其满足全局质量最小，其优化数学模型表达为式（13）。

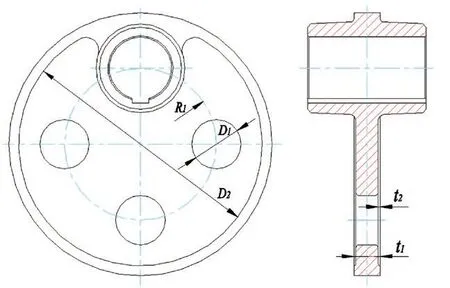
图4 优化变量设置

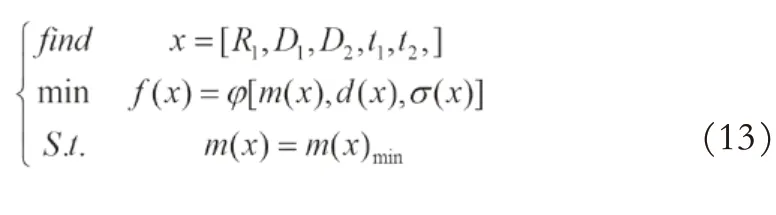
2.2 参数敏感性分析

不同优化参数对优化目标的贡献不同，取优化参数为连续参数，样本容量N＝1 000对设计参数进行敏感性分析，结果如图5所示。分析可知，偏心轮的总质量受偏心轮厚度t1和切除厚度t2影响较大，受开孔直径D1、偏心轮切除部分直径D2影响次之；最大等效应力受偏心轮厚度t1影响较大，受偏心轮切除部分直径D2和切除厚度t2次之；最大总变形受偏心轮切除部分直径D2影响较大，受偏心轮厚度t1和切除厚度t2影响次之。

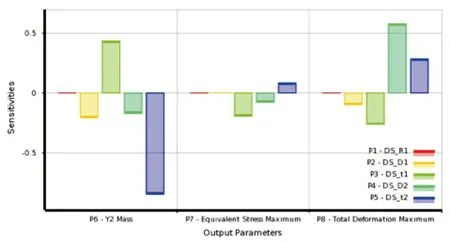
图5 参数敏感性分析

结合参数敏感性分析结论，并考虑本课题的优化目的和实际应用时尺寸的工艺特点，优化约束条件可表达为：

2.3 优化结果

根据第2.2节中边界约束条件下的离散参数个数，优化样本容量，考虑不同设计因素，以偏心轮质量最小筛选样本，并给出不同强度安全系数下的6组最优Pareto解，如表2所示，结论对进一步深化研究提供重要指导意义。

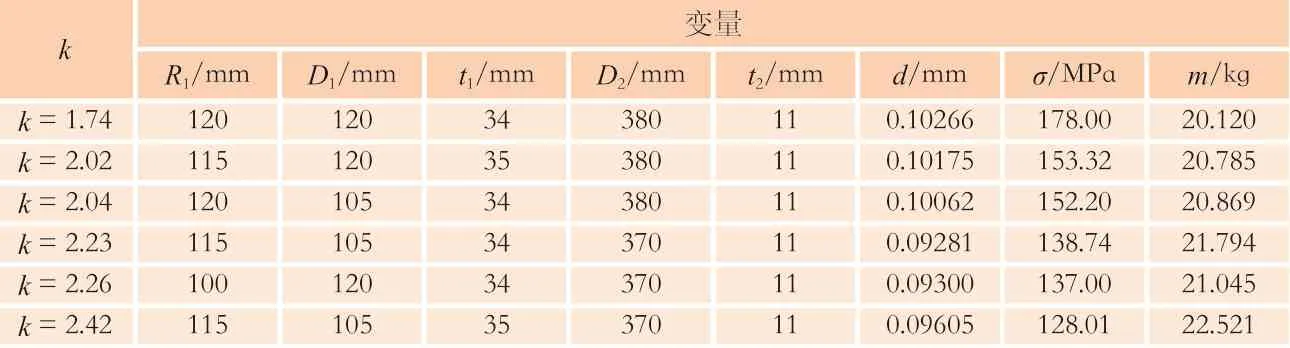
表2 不同安全系数下的Pareto解

考虑到设备低速重载及间歇性载荷特点，基于工程经验，本文建议工程实践中取强度安全系数k=1.1时的屈服强度为许用强度，即［σ］＝282 MPa，并以此许用强度为失效准则取优化结果k＝2.26的Pareto解为本文参数最优组合并讨论优化结果，如表3所示。研究结果表明，在偏心轮质量减重率为43.55%且强度安全系数显著提高的同时，刚度依然满足许用值，优化结果显著。

表3 安全系数k=2.26时优化前后对比

3 讨论

3.1 特殊位置等效应力检查

优化参数R1和D1的组合影响偏心轮有效径向尺寸，该尺寸过小可能会导致特殊位置接触应力过大。图6分析了起始位置（θ＝0°）、最大法向接触力位置（θ＝80°）、近端切除孔位置（θ＝113.6°）、远端切除孔位置（θ＝180°）处的最大等效应力。研究表明，随着偏心轮轴向厚度的减小，远端切除孔位置处的承载能力逐渐减弱，最大接触应力σ＝263.33 MPa满足许用强度。

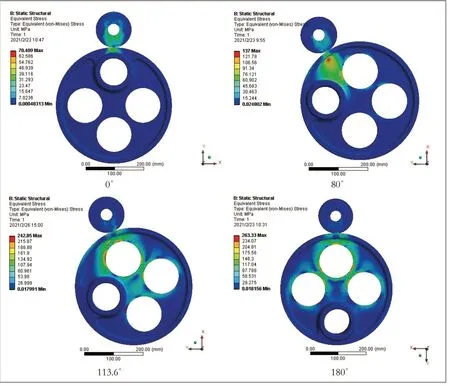
图6 特殊位置等效应力检查

3.2 优化模型抗振能力检查

优化参数t1和t2的组合影响偏心轮的有效轴向尺寸，该尺寸过小可能会导致偏向轮的动态刚度不足，图7分析了优化后模型最大法向接触力处的自由振动特性。研究表明，偏心轮传动机构一阶振型表现为180°位置处沿Z轴正向振动，二阶振型与一阶振型运动相反，三阶振型表现偏心轮0~180°范围内沿Z轴负向和180°~360°范围内沿Z轴正向的振动，四阶振型表现为165°~210°范围内沿Z轴正向的振动和120°~165°及210°~255°范围内沿Z轴负向的振动，且一阶频率为148.08 Hz，满足工程需要。

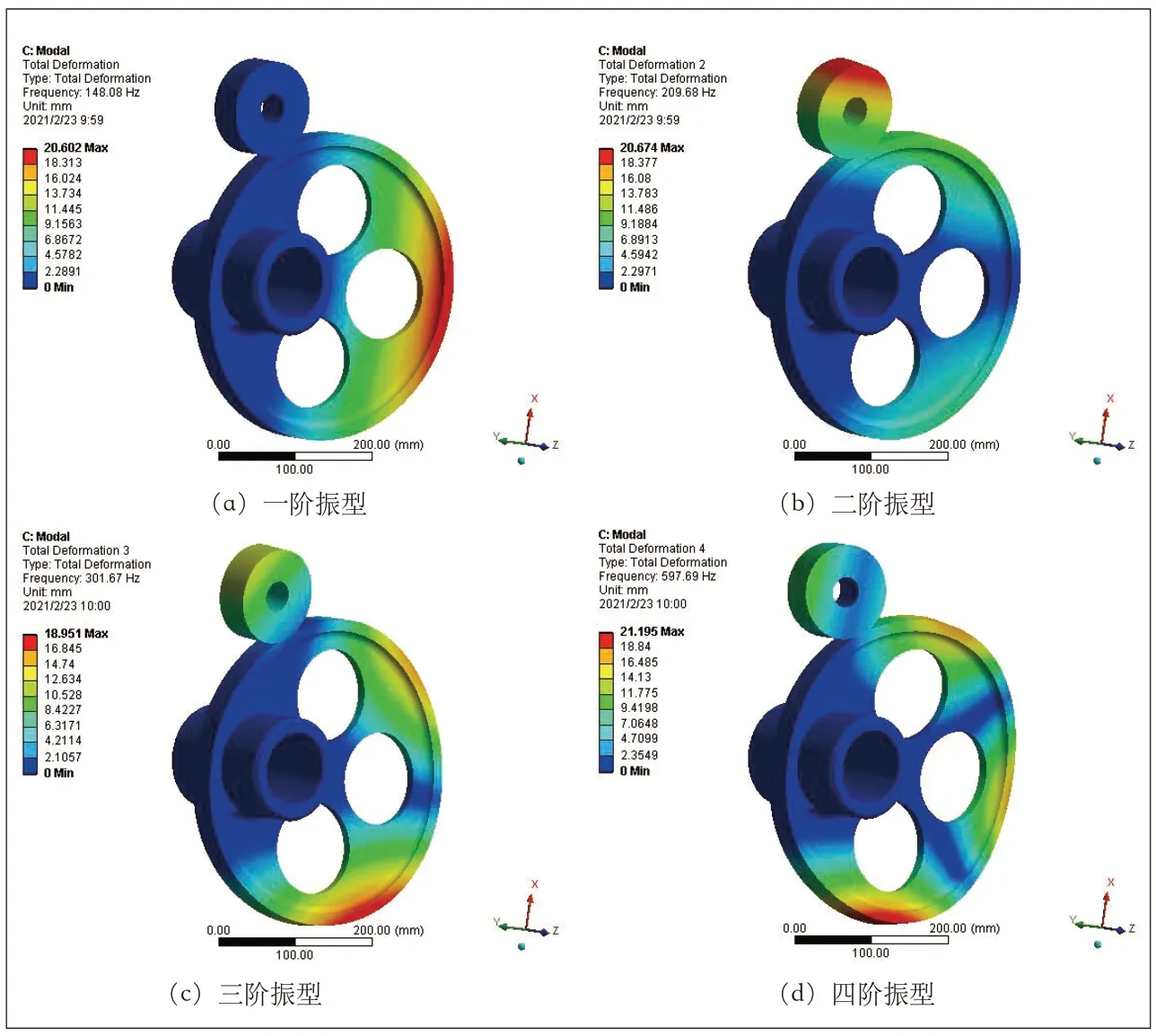
图7 优化后偏心轮的低价振型

4 结论与展望

本研究以演艺装备领域补偿台的偏心轮机构为研究对象，通过运动分析获得了补偿台偏心轮机构的最大压力角、补偿台升降的最大运行速度和最大运行加速度以及运动周期内最大耗损功率，为偏心轮的设计提供可靠的理论依据。进而以载荷最恶劣处的参数建立优化模型对主动偏心轮进行优化设计，获得偏心轮“最优”结构参数组合，主要结论如下：

（1）偏心轮角位移θ＝90°时，压力角最大αmax＝±26.21°，小于许用压力角[α]＝30°，即设计的偏心轮机构有较高的传动效率；偏心轮角位移θ＝180°时，承载轮位移最大smax＝231 mm满足台面行程要求。

（2）位 移 最 大 位 置处（θ＝180°），承重轮速度υ＝0，加速度amax＝±684.05 mm/s2，运动高副无刚性冲击但存在柔性冲击，并且在运动周期内θ＝110°时，起升、下降速度达到最大υmax＝±256.51 mm/s。

（3）运动周期内，偏心轮角位移θ（t）＝80°时偏心轮与承重轮法向接触力最大Fn＝62.91 kN。偏心轮角位移θ＝110°时，承重轮所需外部功率最大Pmax＝±14.12 kW。

（4）给出不同强度安全系数k时的多目标优化函数的Pareto解集，可供设计人员灵活选用。文中选用强度安全系数k＝2.26时的Pareto解x＝[100,120,34,370,11]为最优参数组合。该优化参数下，结构的最大变形dmax＝0.093 mm，最大应力δmax＝137 MPa，mmax＝21.045 kg，轻量化比率为43.55%。

（5）该优化模型中，优化参数t2对质量影响最为敏感；优化参数t1对最大等效应力影响最为敏感；优化参数D2对最大变形影响最为敏感，优化后模型特殊位置处最大等效应力和动态刚度满足许用值。

（6）通过研究承重轮运动学问题和运动过程中的力学问题发现该偏心轮机构虽无刚性冲击但仍存在柔性冲击，设计并优化出性能更好的偏心轮轮廓曲线将是本课题进一步的研究内容。

致谢：感谢魏发孔教授的指导。