直线驱动器传动系统动力学仿真分析

潘国威,陈文亮,王少游

(南京航空航天大学 机电学院，江苏 南京 210016)

直线驱动器传动系统动力学仿真分析

潘国威,陈文亮,王少游

(南京航空航天大学 机电学院，江苏 南京 210016)

以直线驱动器定轴齿轮和行星齿轮组合的传动系统为研究对象，阐述其传动原理，采用多刚体动力学理论建立该传动系统动力学模型，并通过Gear预估-校正算法对动力学方程进行分析。利用ADAMS建立直线驱动器传动系统动力学仿真模型，求解直线驱动器传动系统的传动特性和动态响应，将仿真啮合力与理想情况进行对比，验证了仿真模型的正确性，为直线驱动器的进一步优化及应用提供理论基础。

直线驱动器；传动系统；动力学；齿轮；ADAMS

直线驱动器采用电机驱动，可实现自动化控制，并且该驱动器安装空间小，是取代液压、气压驱动装置的理想产品。现有的直线驱动器减速器一般为单级定轴齿轮传动，存在传动比小、输出直线速度低和承载力小等缺点。本文提出一种将定轴齿轮和行星齿轮组合设计的减速传动系统，行星齿轮传动具有传动比大、传动效率高、传动平稳、体积小及寿命长等一系列优点[1]，因此该传动系统具有传动比大、直线输出速度高、结构紧凑和承载力大等优点。传动系统的传动特性和动态响应是影响直线驱动性能的主要因素，ADAMS为直线驱动器齿轮传动系统动态性能分析提供了很好的平台[2-5]，因此借助ADAMS对直线驱动器传动系统进行运动学和动力学分析与仿真，得到直线驱动器传动系统动态响应情况，为进一步改善直线驱动传动系统动态性能、优化传动系统结构提供理论基础。

1 直线驱动器传动原理

1.1传动系统结构

目前直线驱动器所用的减速传动系统一般为定轴传动机构，而行星齿轮传动应用较少。对于大承载力的直线驱动器，要求齿轮传动系统有更大的承载能力、传动比和传递扭矩。在相同传动比下，使用行星齿轮的减速机传动比大、负载高，安装空间小，因此本文研究的直线驱动器采用两级传动形式：第一级为定轴直齿轮传动，第二级为行星齿轮传动。

1.2传动系统传动原理

直线驱动器传动系统原理如图1所示。通过电机依次带动齿轮1和齿轮2，齿轮2带动与其共轴的太阳轮4，太阳轮4带动3个均布的行星齿轮3，行星轮将运动传递给行星架H，行星架H和丝杠固连，实现直线驱动器直线运动。

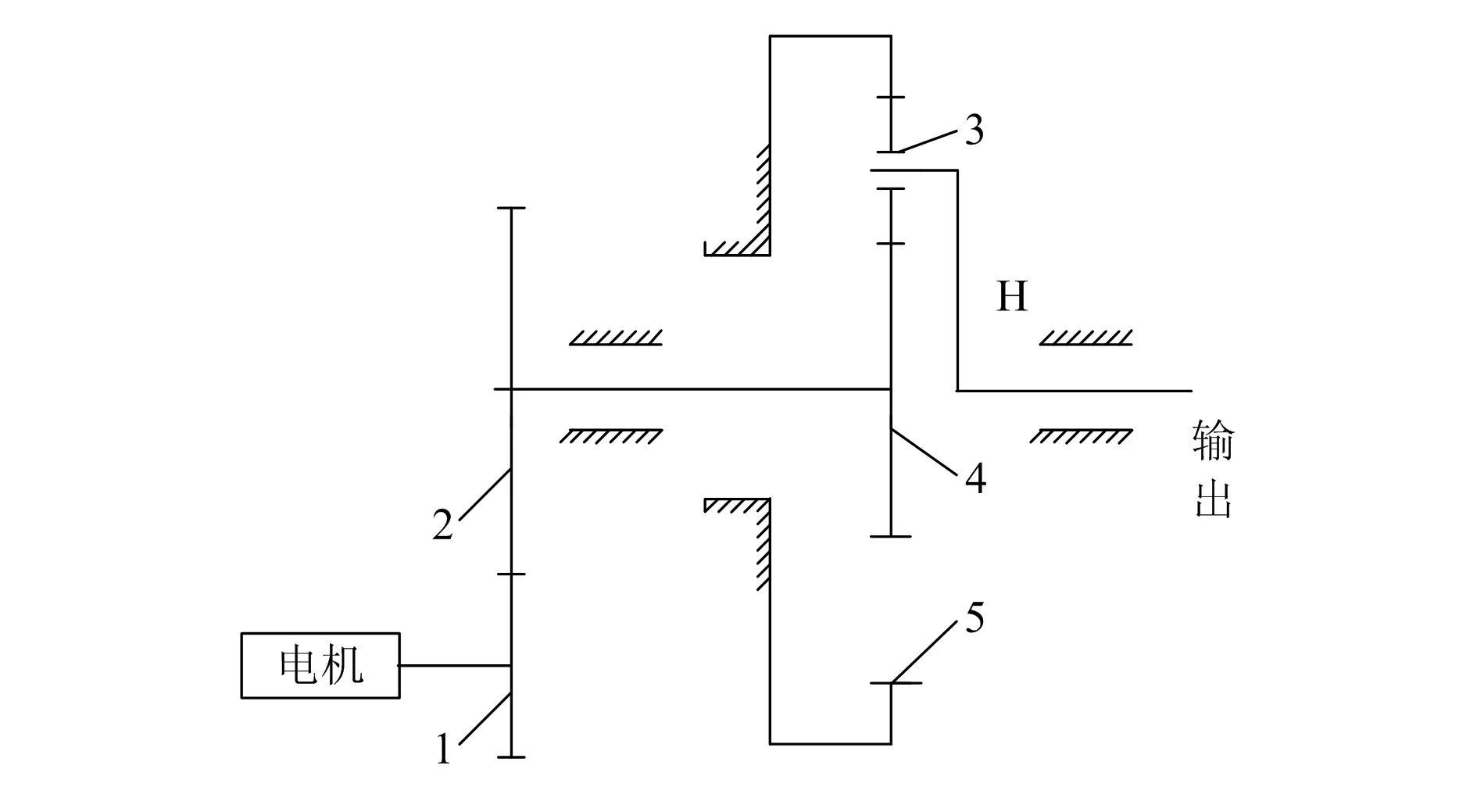
图1 两级传统系统原理图

各齿轮模数为3，压力角为20°。一级齿轮1齿数为35，齿轮2齿数为60；二级太阳轮4齿数为32，行星轮齿数为25，内齿圈齿数为82。根据上述各齿轮参数，结合行星齿轮传动理论[6]，计算传动系统的传动比为：i=60/35×(82/32+1)=6。

2 直线驱动器传动系统动力学建模

2.1动力学方程建立

直线驱动器传动系统主要由齿轮、轴和轴承等构件组成，仅考虑各构件刚性，则传动系统多刚体动力学系统可以由非自由质点系来表示。根据各刚体质点的广义坐标写出传动系统的拉格朗日方程，在此方程基础上进行拉格朗日乘子处理，得到直线驱动器传动系统的微分方程。

(1)

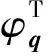
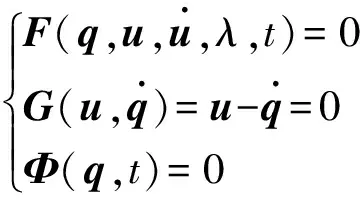
(2)

式中：λ为约束反力；F为直线驱动器系统动力学微分方程；Φ为系统约束方程列阵。

2.2动力学方程求解

针对直线驱动器多刚体传动系统动力学方程，采用Gear预估-校正算法对方程进行求解。根据当前时刻的直线驱动器传动系统状态矢量，用泰勒级数预估下一时刻直线驱动器传动系统的状态量：

(3)

式中：时间步长h=tn+1-tn。经过预估算法得到的新时刻的系统状态矢量通常不准确，这时需用Gear+1阶积分对求解算法进行校正，即：

(4)

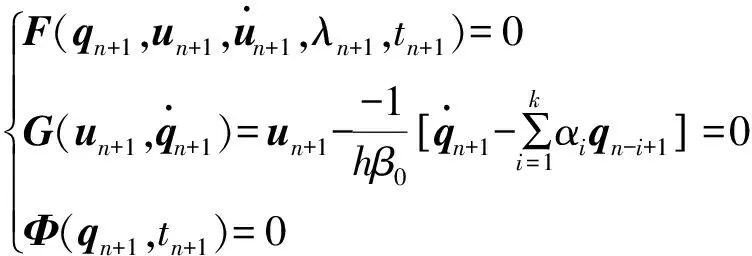
(5)

用修正的Newton-Raphson程序求式(5)，迭代校正公式为：

(6)

式中：j代表第j次迭代；Δqj=qj+1-qj；Δuj=uj+1-uj；Δλj=λj+1-λj。

由式(4)可知

(7)

联立式(1)、(6)、(7)，可得：

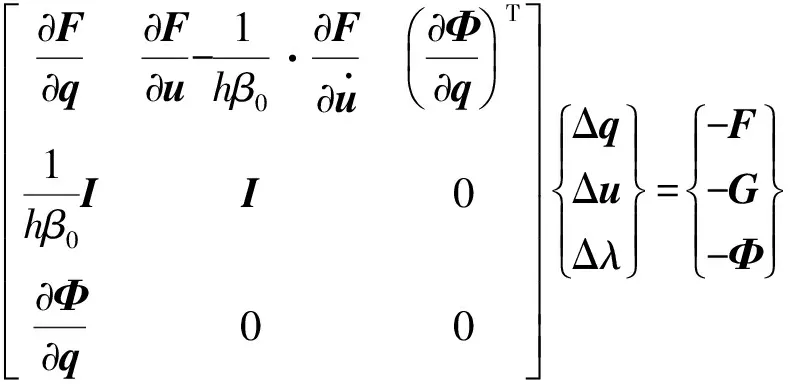
(8)

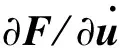
3 仿真与分析

根据建立的直线驱动器传动系统动力学方程，在ADAMS中对直线驱动器虚拟样机进行动力学仿真参数设置，对动力学特性进行仿真求解。

3.1仿真模型建立

直线驱动器传动系统通过相互啮合的齿轮来实现运动和力的传递，在ADAMS中可通过建立相互啮合齿轮间实体碰撞副来模拟齿轮传动，需要设置齿轮的啮合刚度系数K、碰撞力指数e、阻尼系数C、最大阻尼时的击穿深度d等碰撞参数。通过在啮合齿轮对间添加实体-实体碰撞接触力，来分析传动过程中的啮合力。根据直线驱动器传动原理，分别对啮合齿轮副进行运动副设置，添加旋转副、约束副和接触副。直线驱动器模型如图2所示。

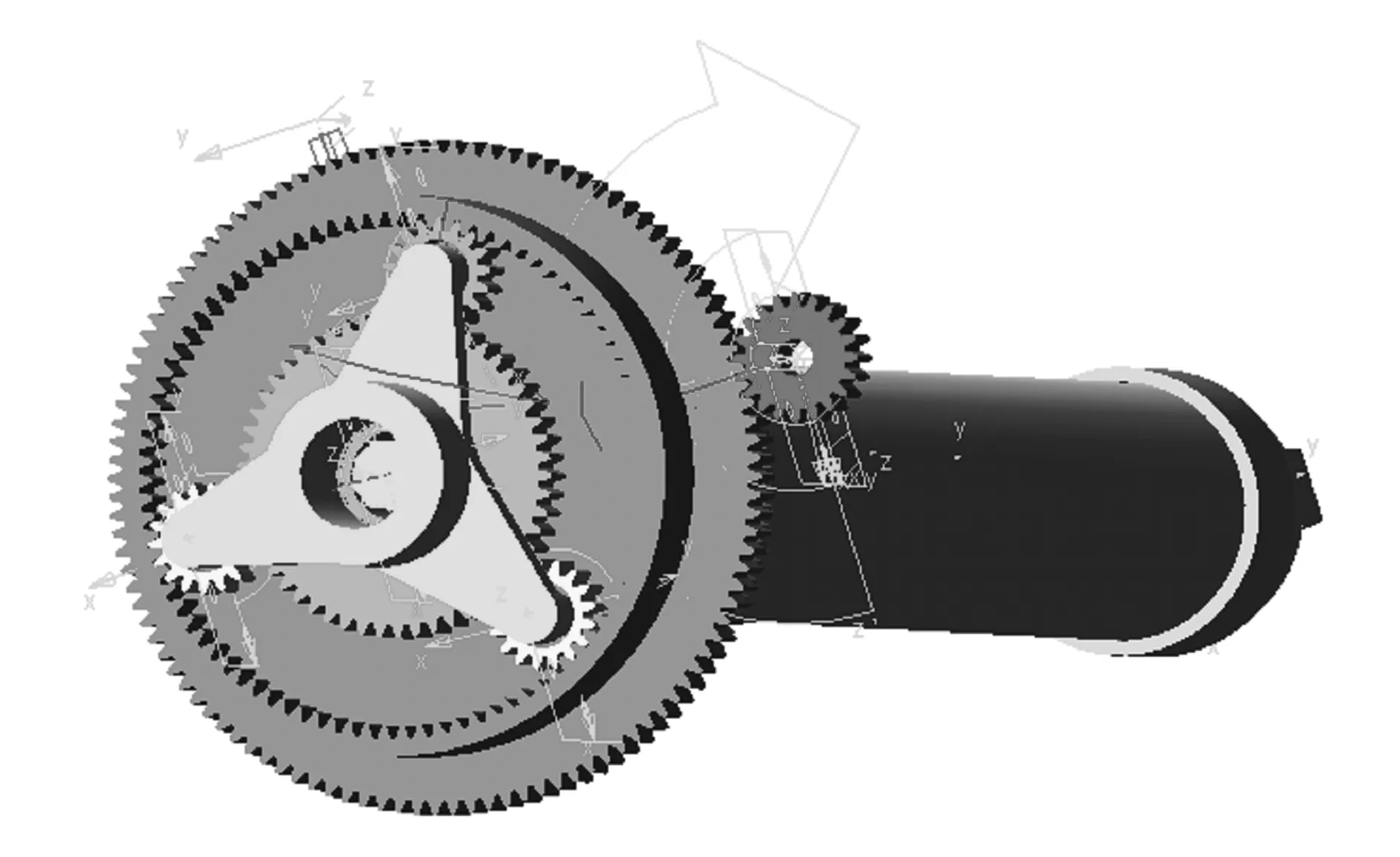
图2 运动约束施加后的直线驱动器模型

3.2仿真参数确定

a.接触函数的选择。

在ADAMS中有两类接触力：一类是基于Impact函数的接触力，另一类是基于Restitution函数的接触力。本文根据传动系统动力学方程，选择Impact函数来计算齿轮啮合力。Impact函数以Hertz弹性碰撞理论为基础，用刚度系数和阻尼系数来计算齿轮啮合副间的啮合力。

b.碰撞力的选取。

当齿轮发生碰撞时，碰撞力方向为啮合齿轮接触面的法线方向，碰撞力为：

(10)

式中：K为直线驱动器传动系统齿轮对间啮合刚度系数；x0为初始距离；x为物体碰撞过程中的实际距离；(x0-x)为变形量；e为碰撞力指数；C为阻尼系数；step为阶跃函数；d为两物体接触后的穿刺深度。

c.摩擦力的选择。

齿轮副在瞬时啮合点处存在的相对滑动会对齿轮副间啮合力和摩擦产生影响。在ADAMS仿真计算时，选择库仑摩擦模型，根据直线驱动器齿轮材料参数及工况选择静态摩擦系数为0.08，动态摩擦系数为0.05。同时，ADAMS设置静态滑移速度vs>Error，动态滑移速度vd>5*Error，其中Error为积分误差。

3.3仿真结果分析

直线驱动器传动系统的总传动比为6，滚珠丝杠导程为5mm，则由传动系统的运动特性，可得输出端的速度理论值应为0.15mm/s。根据齿轮参数计算齿轮对1和2啮合刚度系数K12=4.37×105N/mm，行星轮和内齿圈啮合刚度Kpi=4.05×105N/mm，太阳轮和行星轮啮合刚度Ksi=4.37×105N/mm，e=1.5，C=50N·s/mm，d=0.1mm，设置输入驱动速度10 000r/min，在输出端施加60N·m的负载扭矩。则理论上[7]，齿轮1和2的接触力为178N，行星轮上啮合力为197N。

a.传动特性与运动特性分析。

由于存在齿轮侧隙等影响因素，传动系统齿轮啮合过程中存在冲击和振动，因此图3所示的仿真结果显示输出端速度在0.15mm/s上下波动，由图可以看出输出位移呈线性关系。

b.传动系统动态响应分析。

传动系统的动态响应主要表现为传动系统中啮合齿轮对间的啮合力响应，直线驱动器啮合齿轮

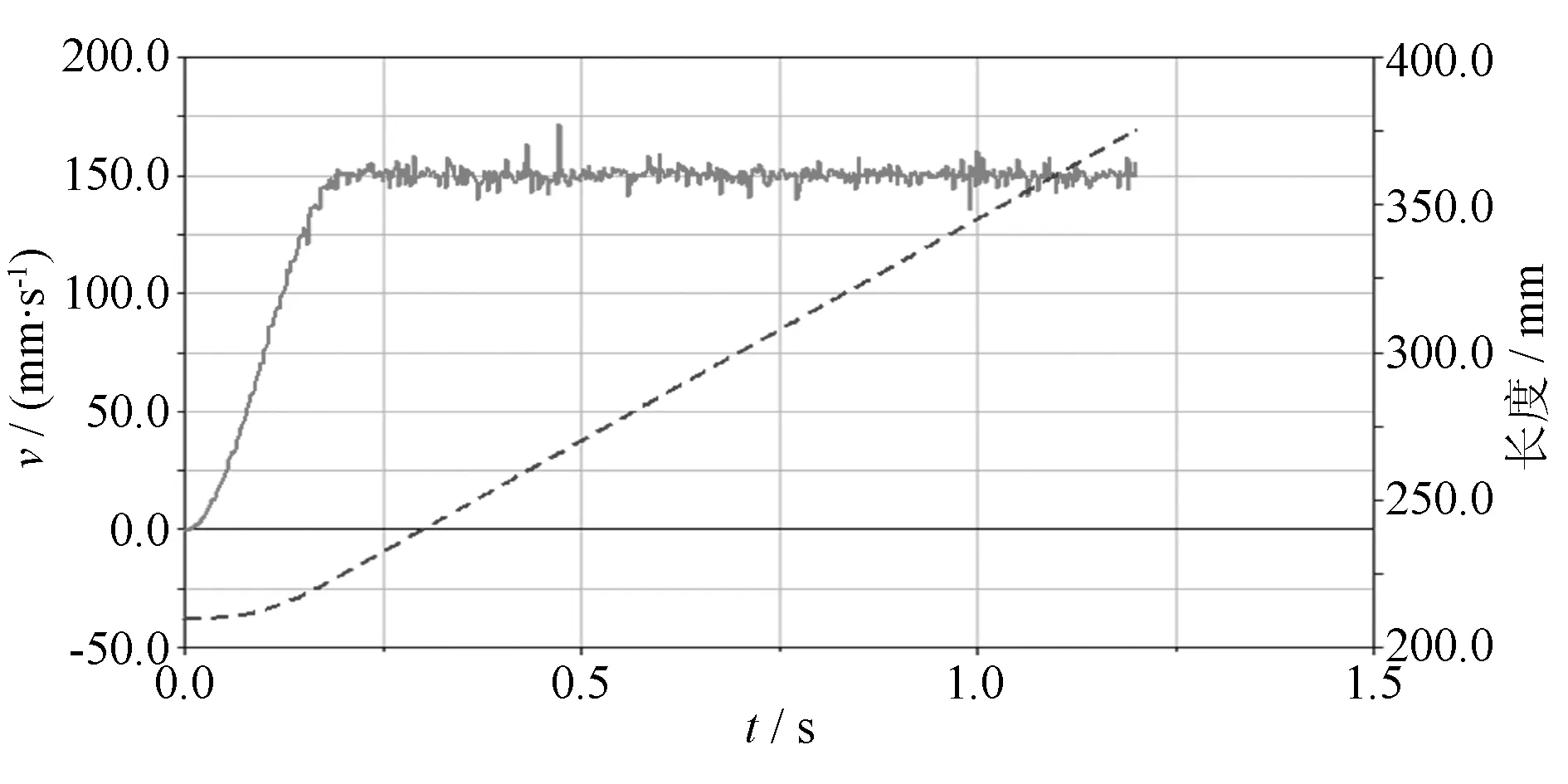
图3 直线驱动器输出端速度和位移

对的啮合力随时间的变化情况如图4、图5所示，由图4可以看出一级齿轮啮合力在190N上下波动，由图5可以看出二级行星轮啮合力在210N上下波动。从图4、图5中可以看出齿轮啮合力中含明显的动载成分，并且啮合力在上下波动，这是由齿轮传动过程中啮合刚度时变性和重合度时变性引起的。齿轮传动载荷分析的振动理论认为，齿轮传动系统是一个弹性的结构系统，在齿轮运转过程中，由于内部和外部的激励，使得整个系统产生瞬态、稳态的振动，引起了啮合过程中轮齿的动载荷。

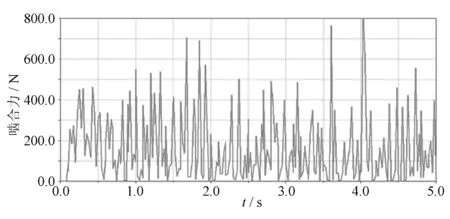
图4 一级齿轮啮合力响应

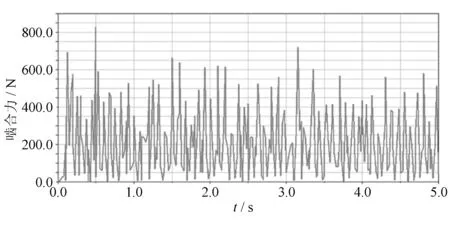
图5 二级行星轮啮合力响应

4 结束语

基于直线驱动器定轴齿轮和行星齿轮两级传动系统原理，建立了传动系统的动力学方程。在ADAMS中建立直线驱动器虚拟样机模型并对其进行运动学和动力学仿真，得到了直线驱动器运动传动特性、运动特性和齿轮啮合力的响应规律。仿真啮合力与理想情况下的计算结果相吻合，说明直线驱动器仿真模型的准确性较高，验证了直线驱动器设计的合理性，为直线驱动器的进一步优化设计及应用提供了理论基础。

[1] 卜忠红，刘更，吴立言.行星齿轮传动动力学研究进展[J].振动与冲击，2010，29(9):161-166.

[2] 赵宁，惠广林，康士朋，等.考虑误差的行星齿轮啮合力仿真[J].计算机仿真，2010，27(5):284-287.

[3] 黄中华，张晓建，周玉军.渐开线齿轮啮合力碰撞力仿真[J].中南大学学报，2011，42(2):379-383.

[4] 赵宁，孙向轩，韩小勇.基于Pro/E与ADAMS的斜齿轮减速器系统动力学仿真[J].中国制造业信息化，2012，41(9):71-73.

[5] 罗卫平，陈曼华，姜小菁，等.发动机配气机构系统的动力学建模及仿真分析[J].中国制造业信息化，2012，41(1):51-54.

[6] 鄂加强，张彬，董江东，等.新型风电偏航减速机动力学仿真分析[J].中南大学学报，2011，42(8):2324-2331.

[7] 占文峰，杜群贵，任少云，等.渐开线行星齿轮啮合力的动态仿真[J].机械设计与制造，2007(8):71-73.

[8] 李增刚. ADAMS入门详解与实例[M].北京：国防工业出版社，2006.

TheDynamicSimulationandAnalysisontheLinearActuatorTransmissionSystem

PAN Guowi, CHENG Wenliang, WANG Shaoyou

(Nanjing University of Aeronautics & Astronautics, Jiangsu Nanjing, 210016, China)

Aiming at the new linear actuator transmission, it introduces the transmission composed of parallel axis gear and planetary gear, establishes the dynamic model of the transmission system based on multi-body dynamics theory, analyzes the dynamic model with gear prediction and correction method. It builds the virtual prototype of linear actuator in ADAMS, solves the dynamic response of the transmission system. The results provide theoretical basis for design and application of the linear actuator transmission system.

Linear Actuator; Transmission System; Dynamic; Gear; ADAMS

10.3969/j.issn.2095-509X.2014.03.004

2013-12-24

潘国威(1988—)，男，江苏连云港人，南京航空航天大学硕士研究生，主要研究方向为机械传动及动力学。

TH132.4

A

2095-509X(2014)03-0015-04