基于中值与均值滤波的边缘检测优化算法*
徐 倩,黄光亚
(吉首大学信息科学与工程学院,湖南 吉首 416000)
基于中值与均值滤波的边缘检测优化算法*
徐 倩,黄光亚
(吉首大学信息科学与工程学院,湖南 吉首 416000)
图像在采集过程中容易受到视角、尺度、亮度、污渍、模糊等不确定因素的影响,造成较大失真.为减少失真,提高边缘提取的精度,在多噪声环境下,提出了中值与均值滤波相结合的边缘检测优化算法,实验仿真结果表明,该算法能有效抑制噪声,能提高图像边缘提取的精度.
中值滤波;均值滤波;PSNR;NMSE
在信息传播领域中,图形和图像发挥的作用也越来越大.据统计,高度信息化的当代,视觉信息成为了人类获取信息的最重要途径,所占比列在75%-85%之间.边缘是图像的轮廓信息,灰度阶跃变化的像素的集合,图像的基本属性之一.图像边缘是由灰度阶跃变化的像素构成的,所以可以从邻域像素灰度函数不连续来检测边缘,对图像周围的像素设计算子进行边缘提取.边缘检测去除了图像背景中不相关的信息,保留图像中主要特征属性的信息,减少了图像操作过程的数据量,提高了后续图像分割、图像识别等图像处理操作的效率.
文中对中值与均值滤波进行分析,并结合2种滤波方法,设计了基于中值与均值的边缘检测算法.这种优化的算法的思路是:对多噪声缘干扰的图像分别进行中值滤波和均值滤波,然后将2种滤波后的图像信号进行边缘提取,最后对2种边缘提取信号进行与运算,得到了最优边缘信号.
1 传统的中值滤波与均值滤波
图像在采集与数据传输及图像处理过程中会混入一些噪声.图像滤波在最大程度的保护图像特征下,排除噪声的干扰.
1.1中值滤波


(1)
如:序列为{0,3,4,0,7},重新排序后的中值滤波为序列为{0,0,3,4,7}中间的值为3.{Xij}二维数据的中值滤波可以表示为

(2)
其中A为滤波窗口.模板尺寸大小决定在多少个像素点中取中值,其形状决定计算像素中值的空间范围.中值滤波运算方法简单,容易实现,方便易执行,滤除椒盐噪声有效.但该方法在滤除噪声时也会严重损失信号的高频信息,滤波窗口内的极值在处理过程中都判为噪声,使得图像的边缘等细节模糊.
1.2均值滤波



(3)

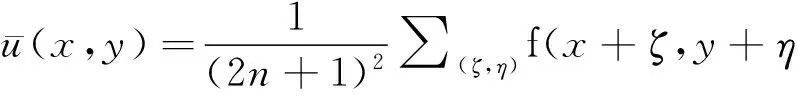
(4)
其中:ζ,η∈[-n,n] ;n为该模板中像素总个数;n×n为模板尺寸.滤波效果与邻域范围相关,模板尺寸选取过大,会使得图像模糊程度更深;模板尺寸选择过小,滤波去噪能力则降低.因此模板大小的选择是滤除噪声与保留图像细节的一种平衡.均值滤波算法简单,计算速度快,这种滤波器适用于去除图象中的高斯噪声.
2 中值与均值优化边缘检测算子
不同的滤波方式抑制不同的噪声,当同时存在多种噪声时,相对而言,中值滤波和均值滤波的效果较好.笔者提出一种优化的基于中值去噪与均值去噪的边缘检测算法.优化算法的原理图如图1所示.

图1 基于中值去噪与均值去噪的边缘检测算法原理
3 评价机制
建立客观的评价机制评估算法的性能,能够实现优化算法和指导新算法研究.评价函数是对去噪算法进行客观评价的通用方法.有2个常用性能指标用于评价去噪效果:正则均方误差值NMSE(被评估图像与原始图像之间的差异程度);峰值信噪比PSNR(最大信号与图像中噪声的比率).

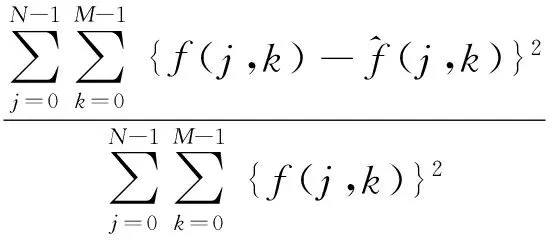
PSNR可表示为[5]

其中:A=255;M×N表示图像尺寸.
4 实验结果与分析
本文比较传统中值、均值算法与本文提出的优化算法3种方法的边缘检测效果,对Lena图,设加载密度为0.05的椒盐噪声、方差为0.01、均值取值为0的高斯白噪声,利用NMSE和PSNR评价函数比较3种算法的边缘性能,检测效果如图2至4所示.
3种算法的边缘检测,其NMSE和PSNR评价函数如图5所示.

图3 均值滤波后各种边缘提取算法的效果
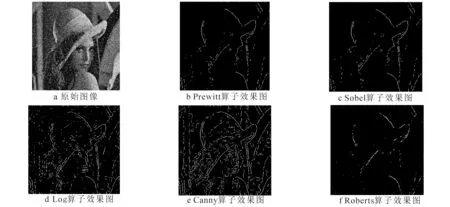
图4 中值与均值结合滤波后边缘提取的效果

a Prewitt算子检测PSNR图 b Prewitt算子检测NMSE图

c Sobel算子的PSNR图 d Sobel算子的NMSE图

e Log 算子检测PSNR图 f Log算子检测NMSE图

g Canny算子检测PSNR图 h Canny算子检测NMSE图

i Roberts算子检测PSNR图 j Roberts算子检测NMSE图
3种边缘检测信号的评价函数如表1所示:

表1 各种算法边缘提取信号的PSNR值与NMSE值
4 结语
图像在多噪声环境下,笔者提出一种中值与均值相结合的边缘检测优化算法.仿真结果表明,文中提出的基于中值与均值结合的边缘检测的优化算法明显改进了边缘提取信号,是一种可执行且优化效果明显的算法.
[1] 朱志恩.中值滤波技术在图像处理中的应用研究[D].沈阳:东北大学,2008.
[2] 王科俊,熊新炎,任 帧.高效均值滤波算法[J].计算机应用研究,2010(2):434-438.
[3] 常瑞娜,穆晓敏,杨守义,等.基于中值的自适应均值滤波算法[J].计算机工程与设计,2008,29(16):4 257-4 259.
[4] 黄小乔,石俊生,杨 健,等.基于色差的均方误差与峰值信噪比评价彩色图像的质量研究[J].光子学报,2007,36(6):295-298.
[5] 佟雨兵,张其善,祁云平.基于PSNR与SSIM联合的图像质量评价模型[J].中国图像图形学报,2006,11(12):1 758-1 763.
(责任编辑 陈炳权)
OptimalAlgorithmofEdgeDetectionBasedonMedianandMeanFilter
XU Qian,HUANG Guangya
(College of Information Science and Engineering,Jishou University,Jishou 416000,Hunan China)
Influenced by the uncertain factors such as viewing angle,scale,brightness,stains,vague,images in the acquisition process are usually distorted;subsequently,the image process with be affected.To reduce the distortion and to ensure the precision of edge detection,this paper put forwards an optimized algorithm of combining median filter with mean filter for edge detection.Simulation results show that this algorithm can effectively suppress noise and improve the precision of image edge extraction.
median filter;mean filter;edge detection;PSNR;NMSE
1007-2985(2014)01-0053-05
2013-08-12
徐 倩(1980-),女,湖南常德人,吉首大学信息科学与工程学院教师,主要从事图像处理、智能检测、电路与系统设计等研究.
TP391.41
A
10.3969/j.issn.1007-2985.2014.01.013

