置于声源两侧的旁通管道噪声自抵消研究

张 浩， 周城光， 刘碧龙， 刘 克

(1.中国科学院 噪声与振动重点实验室(声学研究所)，北京 100190; 2.北京航空材料研究院，北京 10095)

轴流机械在工业生产和日常生活中应用广泛，其带来的噪声问题日益受到人们的关注。轴流机械噪声主要是机械噪声和流动噪声。控制流动噪声主要有安装消声器、敷设吸声材料和主动控制三种方法。

旁通管道，也叫HQ管(Herschel-Quincke Tube)是一种常见的管道消声装置，如图1所示。国内外对HQ管的消声特性已经进行了深入的研究。Selamet等[1-3]用平面波理论研究了普通HQ管的声传递特性，发现当主管道和旁通管道的长度之差为半波长的奇数倍以及长度之和为波长的整数倍时发生共振吸声。接着Selamet等[4]继续研究了只考虑平面波时多个并联的HQ管的传递特性。Torregrosa等[5]和国内的朱之墀等[6]研究了有流情况下HQ管的传递特性。Brady[7]考虑了高阶模态对HQ管吸声效果的影响。Panigrahi等[8]给出了具有各种不同的HQ管的装置传递特性的一般化的算法。Poirier等[9]研究了管道中既有HQ管也敷设吸声材料时的传递特性。但这些研究都是把HQ管安装在声源的同一侧，利用HQ管与原管道的声程差进行消声。

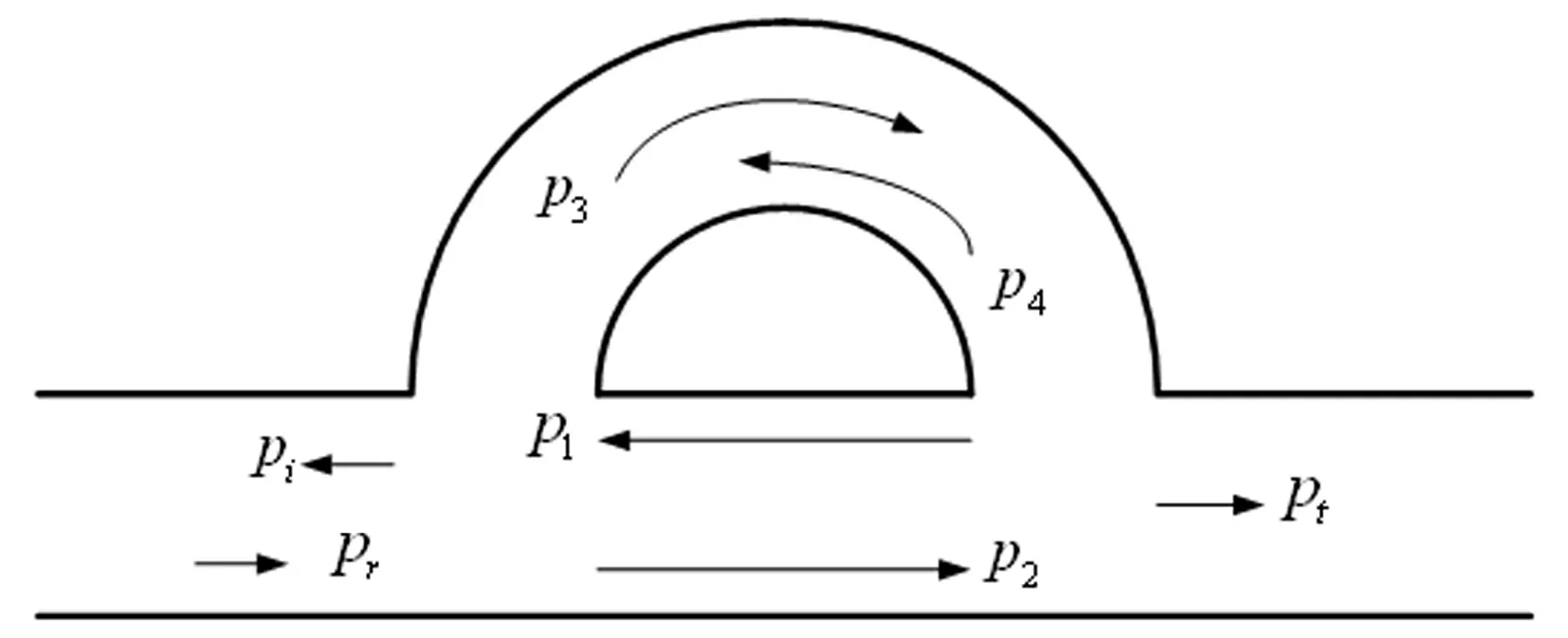
图1 普通Herschel-Quincke Tube 示意图

轴流机械的流动噪声是流体介质与叶轮、导叶等结构之间相互作用[10]引起的，属于偶极子声源[1-3]，但由于管道和流体机械壁面的分隔使其变为两个同幅反相的单极子源[14]，增强了辐射噪声。Bolton等[15-18]对电子产品机箱壁面上的风扇周围的材料进行了改进，使用易于透声的材料，使风扇上下游的声场能连通起来，从而使同幅反相的声波部分抵消，达到噪声控制的目的。Huang等[19]利用加大风扇叶片周围的管道截面积的方法恢复风扇本身的偶极子特性，并在原有管道壁面位置使用薄膜来维持风扇原有流体动力学特性。但是这种结构实施起来有一定的困难。

本文使用旁通管把管道中的轴流机械上下游声场连通起来，对管道中的流动噪声进行控制，采用平面波模型对控制系统进行了分析，并求解得到了系统的插入损失，通过数值仿真和空气管道实验对结果进行了验证。

1 理论模型

图2是一个管道中轴流风扇的示意图。风扇叶片的两侧用旁通管道连接起来，旁通管道和主管道的连接处用透声材料封住以阻隔流体，风扇截面的尺寸与管道内壁截面是一致的。假设管道中为平面波，管道的左端和右端均为全吸收边界，则管道中声场分布如图中所示。风扇向左端和右端辐射声波分别是pL和pR，由于风扇引起的流动噪声具有典型的偶极子特性[11-13]，因此可以认为pL=-pR。p1L和p2L是声源左侧相向的两列行波，p1R和p2R是声源右侧相向的两列行波，p5和p6是旁通管道中相向的两列行波，pLt和pRt是系统向左和向右的出射波。

图2 旁通管道自抵消系统示意图

根据管道中声源的双端口模型[20]，风扇附近的声场满足：

(1)

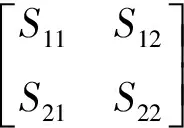
(2)

其中时间项exp(jωt)已经略去。忽略管道中介质流动和透声材料对声传播的影响。Lp是旁支管道的有效长度，文中暂取其轴线长度，Sp是旁支管道的横截面积，LM是主管道中与旁通管道接口位置的距离，SM是主管道的横截面积。共八个方程，p1L，p1R，p2L，p2R，p5，p6，pLt，pRt八个未知数，求解方程组即可得到管道中各部分的声场。

如果散射矩阵是空直管道的散射矩阵，也就相当于忽略了风扇部分对声波的散射作用。求得的声源辐射噪声与出射声波之比为：

(3)

由于pL和pR是无旁通管道时管道中的声压，因此连接旁通管道的插入损失为：

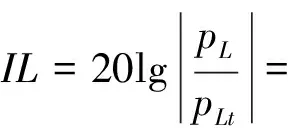
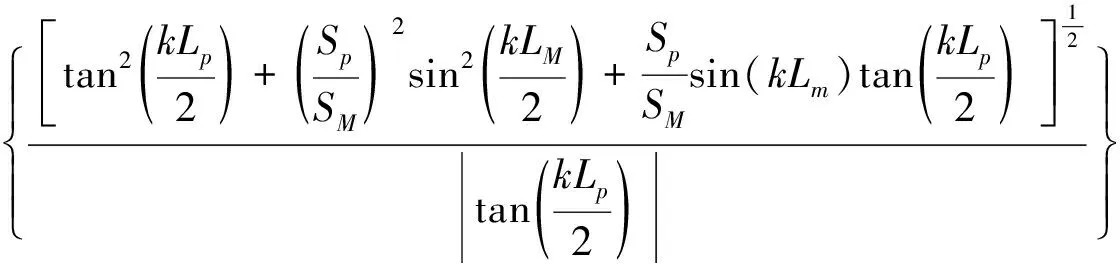
(4)

从三个方面对(4)式进行分析：

① 在sin(kLM)≠0情况下极大值的位置

当Lp=nλ，其中n为正整数，即旁通管道的长度为波长的整数倍时，tan(kLp/2)=0，插入损失有极大值；因为此时旁通管道与主管道的两个连接处是同相位，能使风扇向两侧辐射的反相声波部分抵消。

当Lp=(n-1/2)λ，其中n为正整数。即旁通管道的长度为半波长的奇数倍时，tan(kLp/2)±∞时，插入损失为零；因为此时旁通管道与主管道的两个连接处是反相的，导致加入旁通管道后声波没有任何抵消作用。

②插入损失的正负

令：

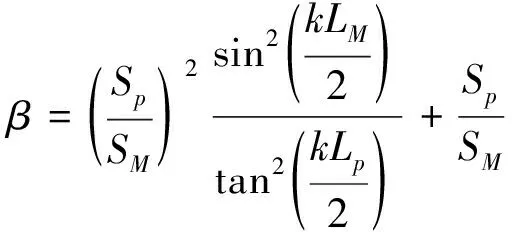
(5)

当β>0时，IL>0；

当β<0时，IL<0；

③ 频率趋于0 Hz时的插入损失：

(4)式在k趋于0时的插入损失的极限为IL=20lg[1+(SpLM)/(SMLp)]。可见当频率趋于0时，系统的插入损失不仅与管道的面积比有关，还与管道的长度有关。旁支管道与主管道的面积比越大，则插入损失越大，长度比越小，则插入损失越大。

图3给出了考虑风扇散射和不考虑风扇散射情况下的连通自抵消管路系统的插入损失。横轴是用c/Lp归一化的频率，纵轴代表插入损失。散射矩阵通过下文中实验测量得到。三个峰值频率对应的波长的整倍数就是旁通管道的长度，此时旁通管道中发生了共振。与传统的旁通管道消声器不同的是，在趋于零频率时，系统的插入损失不是0，而是有一定的插入损失，随着频率升高，插入损失有所下降，，直到旁通管道的有效长度是半波长的奇数倍时，插入损失降为0。

图3 旁通管道自抵消系统的插入损失

图4 水介质管道中低频插入损失

图4中的曲线表示管道中的介质是水的条件下，旁支管道和主管道的面积比和长度比均为1时，旁通管道自抵消结构和普通HQ管结构的插入损失对比。实线和虚线分别是自抵消结构和普通HQ管的插入损失。图中可以看出，应用旁通管道可以有效的降低极低频段的噪声，而普通的HQ管和其他消声器在这些频段的插入损失是几乎为0。

2 数值仿真

对两种管道系统中的声场进行仿真计算：普通管道系统和使用旁通管道的自抵消系统。使用ANSYS进行建模并划分网格，导入SYSNOISE中进行计算。

图5 普通管道示意图

图5是普通管道示意图。管道横截面为正方形，边长为0.1 m，长度为2 m，在管道中央放置一个振动的板作为声源，属于典型的偶极子声源，板为圆形，半径为0.04 m，厚度为0.02 m。振速为0.01 m/s。

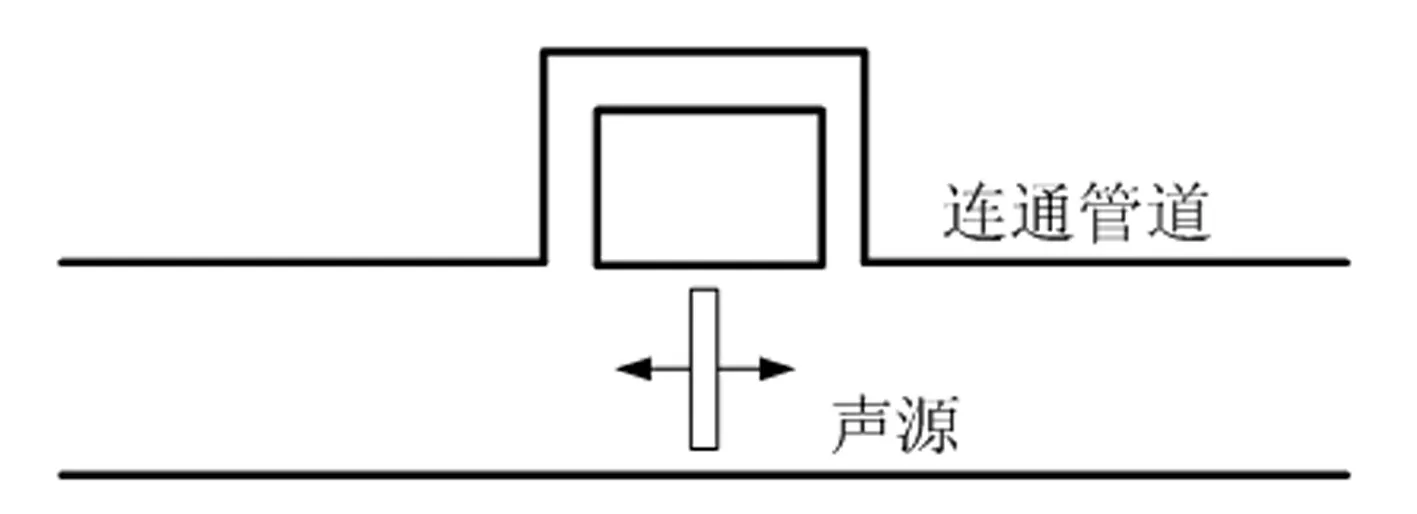
图6 连通自抵消管道

图6是连通自抵消管道，是在图5普通管道的基础上在声源两侧的对称位置添加旁通管道。旁通管道为圆截面直角弯管，截面半径为0.04 m，其它具体尺寸同图9中一致。

使用有限元方法对上述模型的声场进行计算。介质为空气。管道端口阻抗设置为介质阻抗。在管道轴线上距离声源0.5 m处设置场点，旁通管道模型与普通管道场点的声压级之差即后旁通管道模型的插入损失。仿真结果与分析会在下文图18中给出。

3 实验分析

3.1 概述

使用管道中噪声的双端口模型[20]，测量安装在普通管道和旁通管道中的轴流风扇噪声源的传递特性和辐射特性，进而计算自抵消管道的插入损失。使用双端口模型测量得到的声源特性相当于管道两端均为无反射端条件下的声源辐射特性，不会受到测量时管道本身长度的影响。

3.2 实验装置

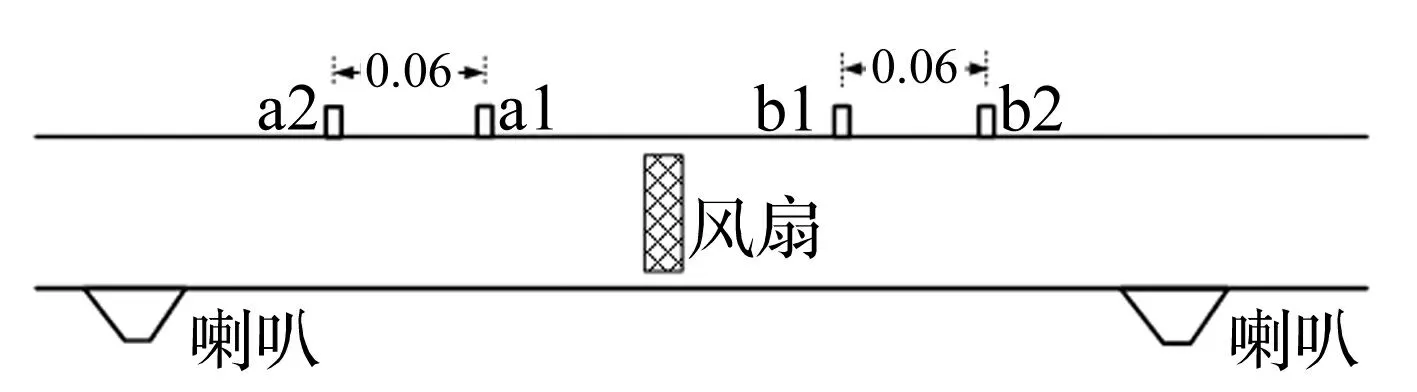
图7 普通管道实验系统示意图

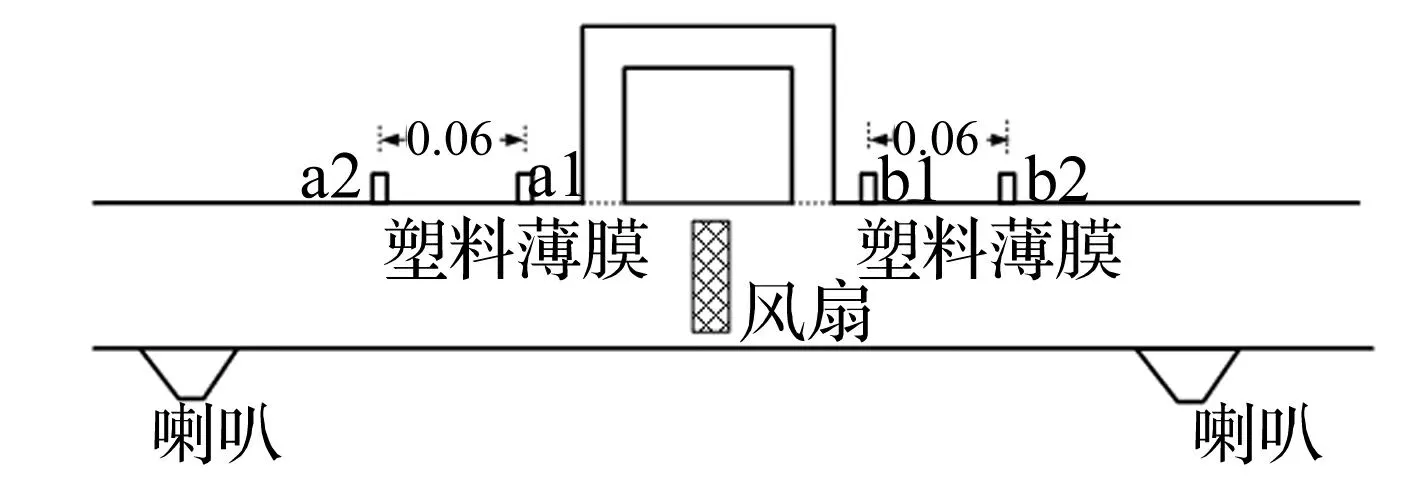
图8 旁通管道自抵消实验系统示意图

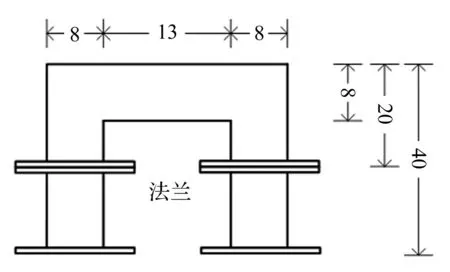
图9 旁通管道尺寸(单位：cm)

图7是普通管道实验系统示意图。噪声源是一个轴流风扇。风扇两侧各有两个传声器，传声器间距为0.06 m。在管道端口附近各有一个喇叭作为外加声源。图8 用旁通管道把风扇前后连接起来，在开口处用塑料薄膜保证流场与普通管道中的流场一致，并且认为塑料薄膜对声波传播没有任何影响。旁通管道有两种尺寸：长旁通管道和短旁通管道。图9 中是长旁通管道的尺寸，去除法兰下面两段直管道，只保留上半部分的为短旁通管道。管道系统的材质是有机玻璃。传声器使用B&K 4189，采集分析系统是B&K PULSE 3560C。图10到图13是实验系统的实物照片。

图10 整体自抵消管路测试系统

图12 普通管道系统

3.3 实验结果

管道的横截面为正方形，边长为0.1 m，因此管道平面波截止频率为1 715 Hz。两组传声器的间距均为0.06 m，频率上限为2 572 Hz，下限为286 Hz。因此本次实验中双端口模型的适用的频率范围是286 Hz-1 715 Hz，下面的分析都选取300 Hz-1 600 Hz。

图14、图15、图16分别是三种情况下的散射矩阵的实部、虚部和声源强度。实线代表普通管道的情况，虚线代表短旁通管道的情况，点划线代表长旁通管道的情况。横坐标均为频率。图14、图15中左上图是声源左端的反射系数，右上图是声源右端透射系数，左下图是声源左端透射系数，右下图是声源右端反射系数。图16中左上图是声源向左辐射声波的自谱，右下图是声源向右辐射声波的自谱，右上图和左下图为向左和向右辐射声波的互谱。

图14、图15中可以看出，安装了旁通管道显著改变了声源部分的散射矩阵，也就是声源部分的传递特性发生了变化。图16表示安装旁通管道后声源辐射特性在某些频段也出现了明显的谷，这些发生变化的频段与图14、图15中发生变化的某些是相互对应的，是旁通管道的抵消作用引起的。同时使用旁通自抵消管道时，有些频率的声压级会有略微的上升，这与平面波理论模型预测是相符的，但是这些上升并不明显。

图17是两种旁通管道相对于普通管道的插入损失。上图代表左端，下图代表右端。横坐标是频率，纵坐标是插入损失。虚线代表短旁通管道，点划线为长旁通管道的结果。可以看出插入损失基本上在绝大部分频段是正值。

图14 三种管道散射矩阵的实部

图17 旁通管道插入损失的实验结果

图18 长旁通管道自抵消系统的插入损失三种方法结果对比

图18分别是长旁通管道自抵消系统的插入损失理论、仿真和实验结果对比。实线是理论计算结果，虚线是仿真结果，点划线是实验结果。整体上看，三条曲线在低频部分符合的较好，而在中高频部分符合的较差，其中仿真结果和实验结果符合的频段要更宽一些。第一个峰值在366 Hz左右，对应的波长约为0.93 m，正好对应于旁通管道的长度。这一长度也大致是第二个峰值和第三个峰值处所在的频率所对应的波长的两倍和三倍。但是第二个峰值和第三个峰值所在频率的实验结果要比理论结果偏低，这说明实验中峰值频率对应的波长比平面波模型预计的波长要长，也就是旁通管道的有效长度有所增加。因为随着频率的增加，波长与管道的尺寸已经可比，此时旁通管道的长度已经不能简单的用轴线的长度计算，因为声波不再是简单的沿着旁通管道的轴线传播，管道的形状对声波的传播影响作用开始显现，而平面波模型则无法捕捉这一影响，才导致频率上的偏移。可以考虑使用对旁通管道的等效长度进行修正的方法来对平面波进行改进。这个工作需要进一步的研究。

图中显示插入损失有三个明显的峰值。理论结果和仿真结果在峰值处都比实验结果高很多，原因是理论模型和仿真模型都没有考虑阻尼带来的影响，而在实验中，阻尼是不可避免的。

4 结 论

对利用旁通管道对轴流机械流动噪声进行自抵消控制的方法进行了理论分析。利用管道连接处的声压和体积速度连续的边界条件，并根据双端口模型考虑了风扇对声波的散射作用，得到了平面波条件下系统的插入损失。使用有限元方法对其进行了仿真计算，并在空气管道中进行了实验验证。

理论、仿真和实验的结果对比表明，利用旁通管道的轴流机械自抵消控制方法有一定的效果，在旁通管道的有效长度等于声波波长的整数倍时效果最为显著。与普通HQ管在趋于0Hz的极低频率插入损失为0不同，这种方法在趋于0Hz的极低频率部分也有一定的插入损失，并与旁通管道及主管道的长度和面积有关。这为管道中轴流机械的低频噪声控制问题提供了新的思路。

仿真和实验结果还表明，平面波理论模型对二阶共振以下的低频的预测较为准确，对二阶以上的中高频段的计算结果则有一定的误差。由于忽略了阻尼，峰值频率处的插入损失也相对实验结果偏高。

参 考 文 献

[1]Selamet A, Dickey N S, Novak J M. The Herschel-Quincke tube: a theoretical, computational, and experimental investigation[J]. J.Acoust.Soc.Am, 1994, 96(5):3177-3185.

[2]戴根华,田 瑞，李 鹭,等. 带旁通的管道中的声能流及传声损失：理论分析[J].声学学报，1995, 20(4):244-249.

DAI Gen-hua, TIAN Rui, LI Lu, et al. Acoustic energy flux and transmission loss in a duct with by-pass, part I:theoritical analysis[J]. Acta Acustica, 1995, 20(4):244-249.

[3]田 瑞,戴根华,王清理，等. 带旁通的管道中的声能流及传声损失：实验研究[J]，声学学报，1995, 20(5):385-392.

TIANG Rui, DAI Gen-hua, WANG Qing-li, et al. Acoustic energy flux and transmission loss in a duct with by-pass, part II:experimental study[J]. Acta Acustica, 1995, 20(5):385-392.

[4]Selamet A, Easwaran V. Modified Herschel-Quincke tube: Attenuation and resonance for n-duct configuration[J]. J.Acoust.Soc.Am, 1997,106(1):164-169.

[5]Torregrosa A J, Broatch A，Payri A. A study of the influence of mean flow on the acoustic performance of Herschel-Quincke tubes [J]. J.Acoust.Soc.Am, 2000, 107(4): 1874-1879.

[6]朱之墀,国 瑞，田 瑞,等.流动管道内利用旁通管道反声降噪研究[J].声学学报,1997,22(1):1-10.

ZHU Zhi-chi, GUO Rui, TIAN Rui, et al. A study of noise reduction by anti-sound using bypass in ducts with flow[J]. Acta Acustica,1997,22(1):1-10.

[7]Brady L A. Application of the Herschel-Quincke tube concept to higher-order acoustic modes in two-dimensional ducts [D]. Blacksburg, Virginia Polytechnic Institute and State University, Master Thesis, 2002.

[8]Panigrahi S N, Munjal M L. Plane wave propagation in generalized multiply connected acoustic filters [J]. J. Acoust. Soc. Am. 2005, 118(5): 2860-2868.

[9]Poirier B, Maury C, Ville J M. The use of herschel-quincke tubes to improve the efficiency of lined ducts [J].Applied Acoustics, 2011, 72:78-88.

[10]Neise W. Review of fan noise generation mechanisms and control methods [A]. Fan Noise-An international INCE Symposium, CETIM, Senlis, France, 1992, 45-56.

[11]Baade P K. Effects of acoustic loading on axial flow fan noise generation [J]. Noise control engineering,1977,8:5-15.

[12]Margetts E J. A demonstration that an axial fan in a ducted inlet ducted outlet configuration generates predominantly dipole noise [J]. Journal of Sound and Vibration, 1987, 117(2): 399-406.

[13]Åbom M, Bodén H. A note on the aeroacoustic source character of in-duct axial fans [J]. Journal of Sound and Vibration,1995,186, (4): 589-598.

[14]Beltman W M. Quantification and modeling of fan installation effects [A]. Inter-Noise 2006, Honolulu, Hawaii, USA.

[15]Bolton J S,et al. Fan Noise Control Apparatus [P]. US 2006/0269077 A1. Nov.30,2006.

[16]Lee M Y, Bolton J S, et al. Fan Noise Control by Enclosure Modification [A]. Inter-Noise 2005,Rio de Janeiro Brazil.

[17]Shin Y A, Bolton J S. Study of the Dipole-like Behavior of Axial Fans [A]. Inter-Noise 2008,Shanghai,China.

[18]Lee M Y, Bolton J S, Yoo T, et al. Reduction of fan noise emission by enclosure modification [J]. Noise Control Eng. J. 2008，56 (1):4-15.

[19]Huang L, Ma X, Feng L G. Suppression of broadband noise radiated by a low-speed fan in a duct [J]. J. Acoust. Soc. Am. 2010, 128(1), 152-163.

[20]Laverentjev J, Åbom M, Bodén H. A measurement method for determining the source data of acoustic two-port sources [J]. Journal of Sound and Vibration, 1995, 183(3):517-531.