地铁振动对既有砌体结构影响规律及因素数值分析

夏 倩， 屈文俊

(同济大学 建筑工程系，上海200092)

城市地铁线路选择通常根据客流预测，近距离经过或下穿敏感建筑不可避免，致使敏感建筑自身结构安全及特殊功能需求受到长期振动潜在影响。近年对地铁振动引起自由场地振动规律研究较多，而对特殊敏感建筑(如医院[1]、精密仪器实验室[2-3]、文物建筑[4-6]、博物馆[7]等)振动影响研究主要集中于预测方法及个案评估[7]。由于建筑本身材料、形态千差万别，对建筑物内振动分布规律研究难度较大。

与建筑形式各异的高层钢结构、钢混结构建筑相比，居住型砌体结构大多建筑形式单一，同一地区所用材料、建筑层数、规模、外形较相似，方便研究其振动分布规律，但对砌体结构振动研究尚少见。为此，本文以上海老城区既有砌体结构受地铁振动影响为研究背景，在地铁沿线两栋居民住宅楼内详细测试分析三正交方向振动响应，建立精细砌体结构数值模型，研究振动响应分布规律，扩充现场测试数据。由于目前国内外研究多集中于新型结构体系受振情况，本文结果不仅能填补砌体结构受地铁振动影响研究空白、实用意义较强，而且可为既有结构隔振方案提供可行性数据。

1 数值模型

地铁车辆引起建筑物振动受振源、传播路径、建筑结构等多因素影响，数值建模时若考虑所有子系统会使问题异常复杂，且会使预测精度下降。本文建立的砌体结构三维有限元模型，利用部分房间内实测数据调整建模参数，并将调整后模型用于分析整座楼各房间的振动响应分布。

1.1 研究对象及模型尺寸

试验场地为上海某段地铁线路。试验现场有2栋普通砖混结构住宅楼，本文以其中1栋楼为研究对象，该楼距地铁中心线10 m。为尽量模拟真实砌体结构振动，数值模型按砌体结构包括楼梯间实际情况建立，见图1、图2，模型边界为固定边界。由于现场采集材料数据有限，仅作参考。程序中取烧结普通砖强度等级MU10，砂浆强度等级M2.5，获得烧结普通砖砌体抗压强度设计值1.30 MPa，并认为砌体施工质量控制等级达到规范[8]中B级水平，取材料性能分项γf=1.6。

fk=γff=1.6×1.30=2.08 MPa

(1)

据文献[9]，砌体强度标准值与平均值关系为：

fk=fm(1-1.645δf)

(2)

式中：fk为砌体强度标准值；δf为砌体强度变异系数。

据《砌体结构设计规范》GB50003-2001条文说明，烧结普通砖砌体强度平均值公式中变异系数δf=0.205。本文所研究砌体结构建造于上世纪60年代，偏低取变异系数δf=0.1。获得砌体强度平均值为：

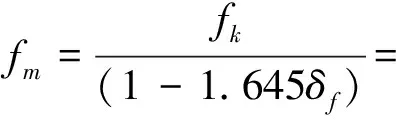
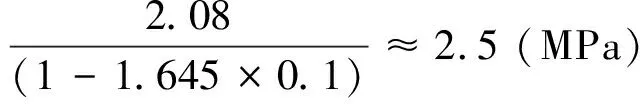
(3)

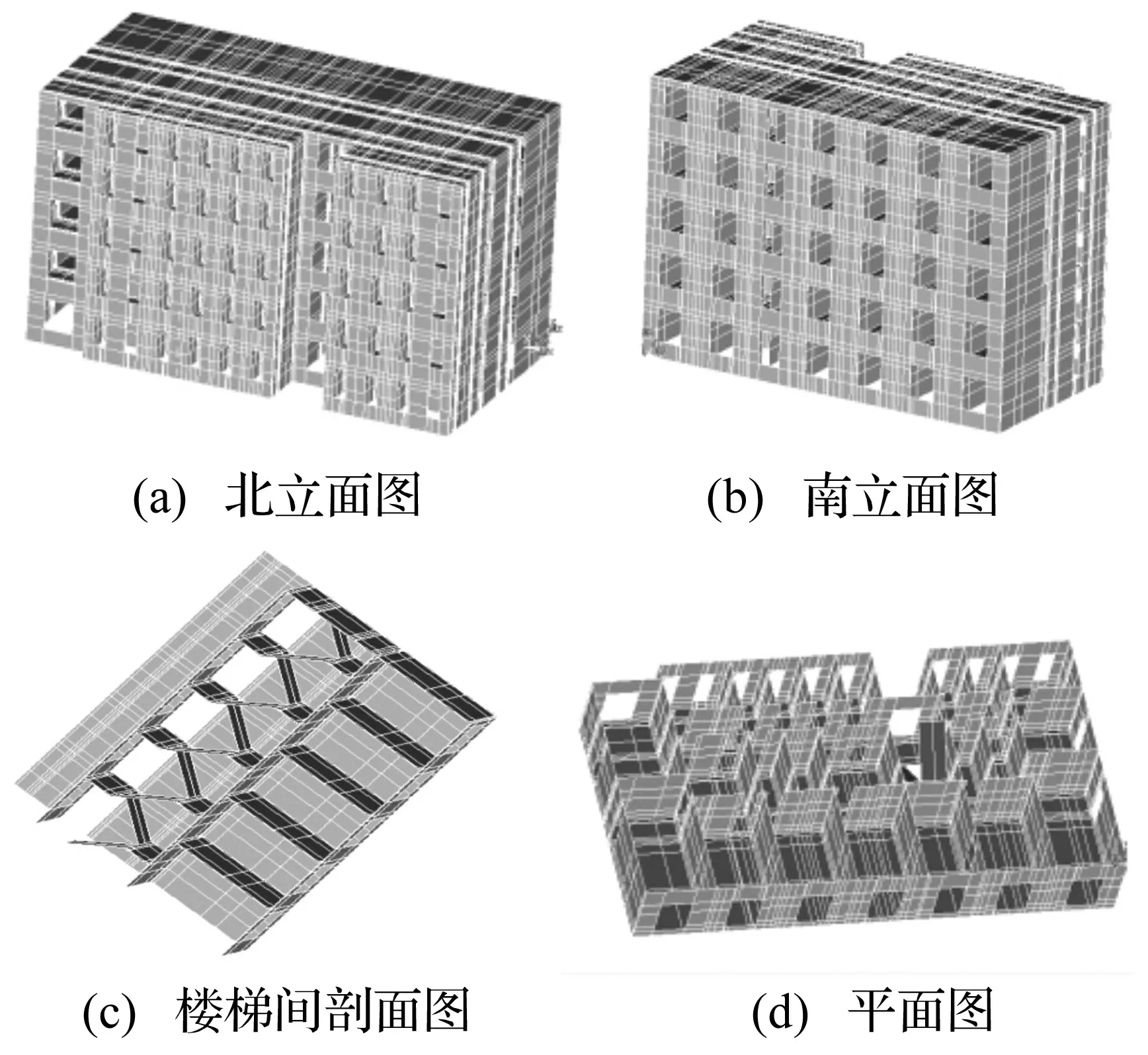
图1 有限元模型图

图2 试验建筑照片

1.2 单元类型与构件截面

该建筑中楼板、墙体用SHELL181单元模拟，梁柱用BEAM188单元，砖墙厚240 mm，用单层SHELL单元，赋予砌体材性；预应力空心楼板厚100 mm，部分现浇楼板厚100 mm，赋予混凝土材性；梁柱截面用用户自定义截面，分别于四角点设置纵向钢筋，见图3，圈梁截面240×240，楼梯梁截面240×300，柱子截面240×240。取圈梁、构造柱截面底部与顶部配筋相同，其纵筋面积As=24×24×2=1152 mm2,则截面底部、顶部纵筋配筋率均为2.0%。

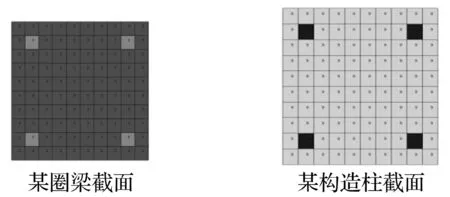
图3 圈梁及构造柱截面

1.3 材料属性及单元尺寸选取

混凝土强度等级C20，抗压强度取设计值fc=9.6 MPa；砌体抗压强度取平均值fm=2.5 MPa；钢筋为HRB335，屈服强度取设计值fy=300 MPa，材料属性见表1。

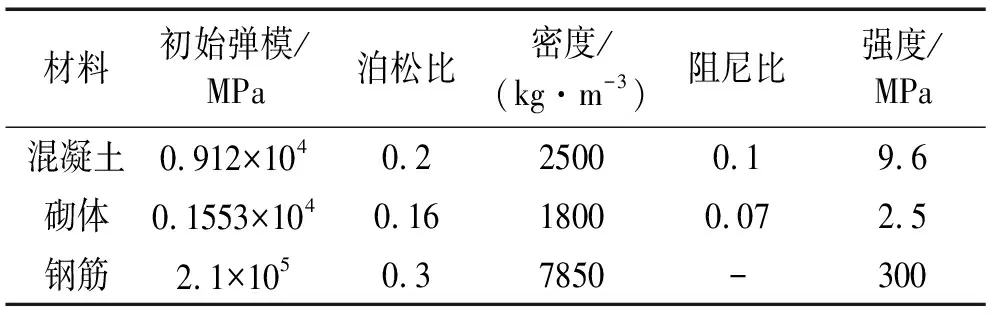
表1 材料属性

为尽量模拟真实结构地铁环境下振动性能，据建议[10]，本文选混凝土阻尼比10%，砌体材料阻尼比7%。划分建筑单元，考虑速度较小弯曲波并按1/8波动细化标准，梁、柱、板单元划分时，单元最大尺寸主要受梁高、板厚影响按80 Hz振动频率为0.5 m，可保证计算精度。

1.4 激励输入

为分析三维模型振动响应规律，不考虑土结构相互作用，采用相对运动法。有研究[11]表明：因环境振动影响时，不考虑土结耦合的建筑振动计算偏安全。试验现场所测地铁经过楼房时建筑底部墙边位置加速度时程为模型激励，持时17.5 s，见图4，并按一致激励法在建筑数值模型底部输入，研究表明[12-13]，该方法对振动响应计算偏于安全。采用Rayleigh阻尼，取建筑基频80 Hz，阵型阻尼比0.05求解阻尼系数。用Newmark直接积分法动力分析，积分步长0.005 s。

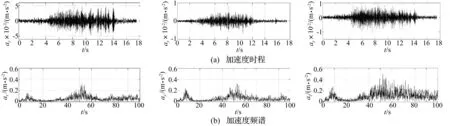
图4 输入加速度时程及频谱

2 模型校核

利用在该建筑2、4层室内房间及3～5层楼梯间所测垂向加速度对模型进行校核。各房间名称及位置见图5。

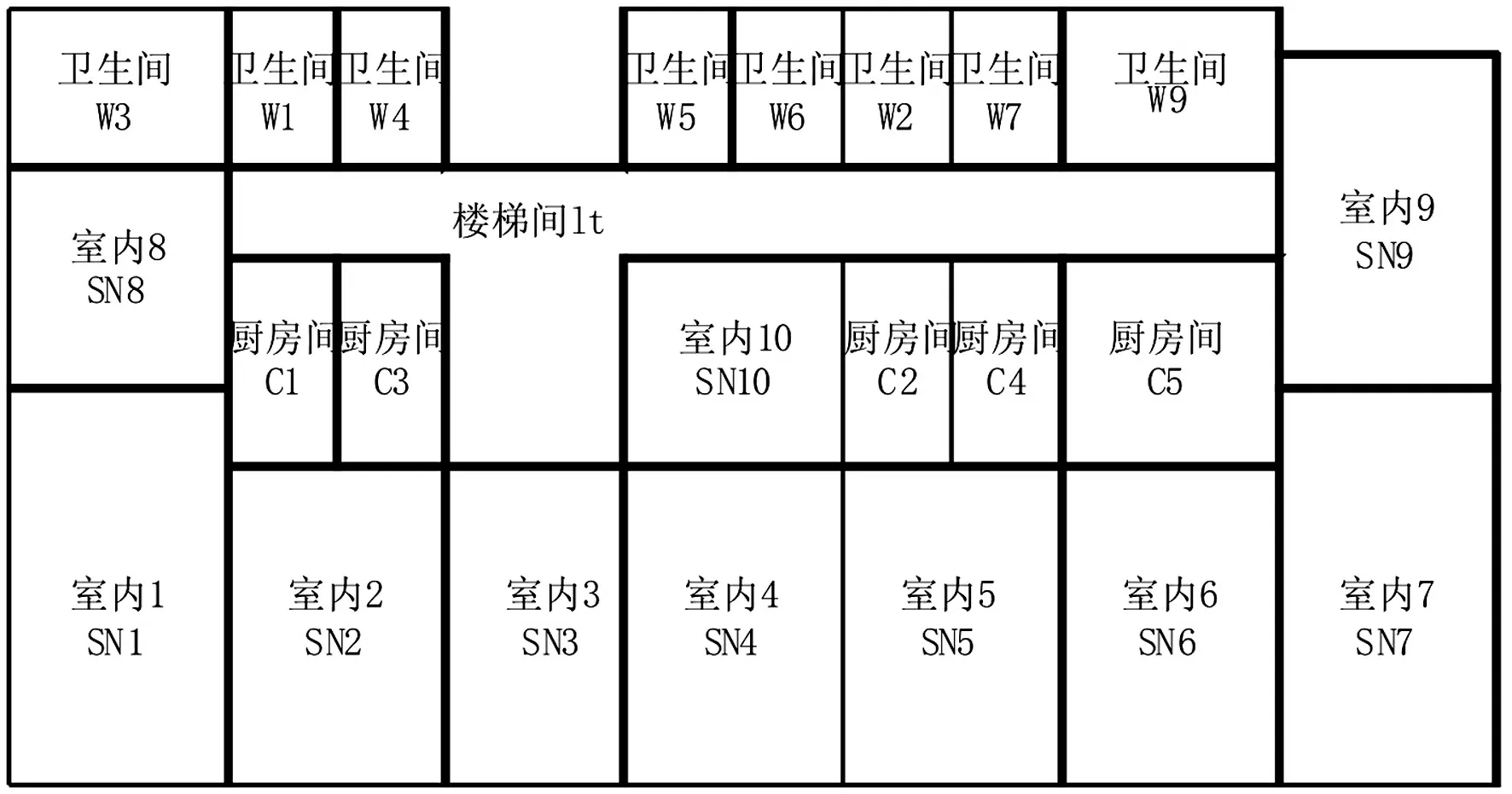
图5 各房间名称及位置

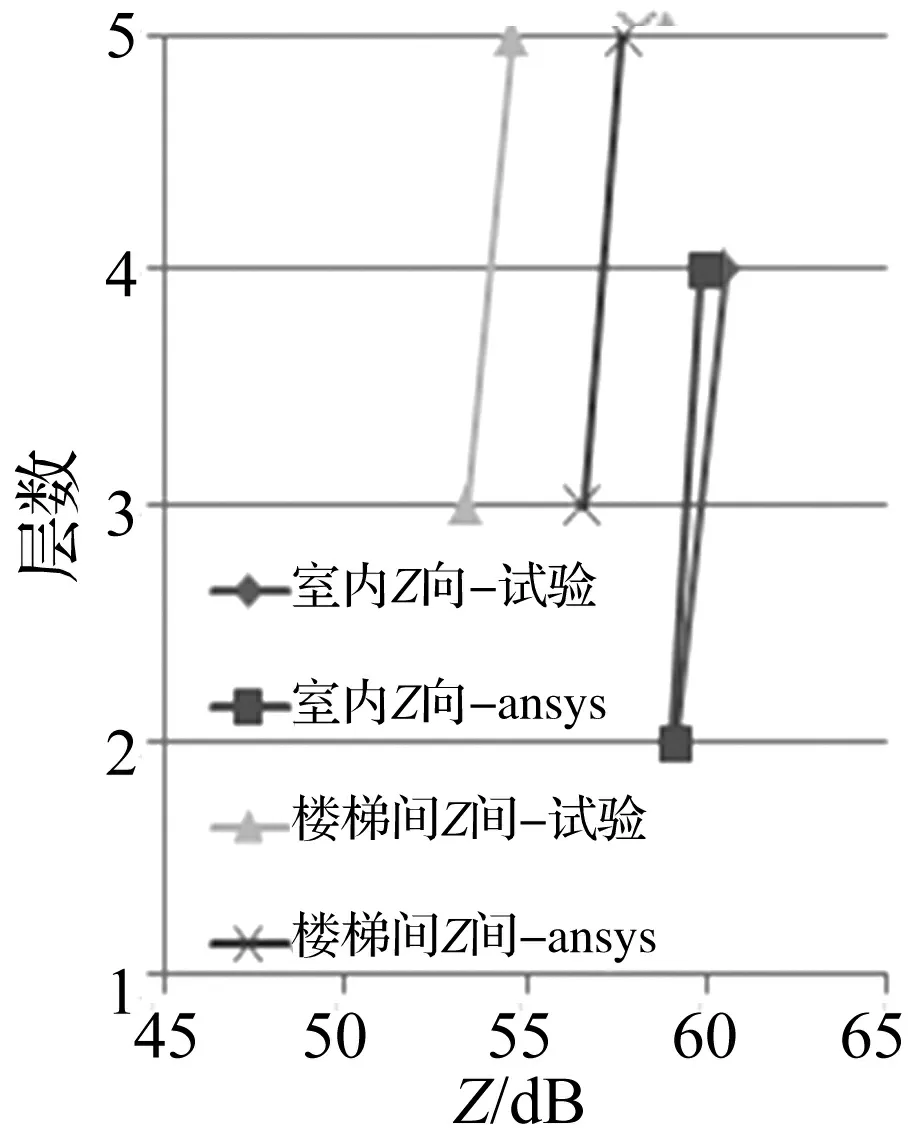
图6 计算值与实测值Z振级对比

图6为计算值与实测值Z振级随层高的变化曲线。可以看出，二者振动响应规律及数值基本一致。由表2看出，最大计算误差为1.4 dB。

2.1 VAL沿楼层高度变化-室内与楼梯间位置

在1/3倍频程频域内对比某楼层不同位置振动响应。限于篇幅，仅给出第四层垂向加速度级，见图7。对比可见，计算值与测试值在各中心频率上均吻合良好。

表2 Z振级计算误差

注：负值表示数值模型结果小于试验结果

3 振动响应规律分析

利用校核后模型分析各楼层不同房间的振动响应规律，弥补测试的局限性。

3.1 振动随楼层变化

3.1.1 楼板中央与墙边振动对比

3.1.1.1Z振级分析

将地铁经过楼房时楼板中央与楼板墙边处竖向振级进行对比，以房间编号SN2，C1，C2，W1，W2及2层、5层为例，两层垂向振动响应见图8。由图8看出，地铁通过时，大跨度室内位置楼板中央竖向振级较楼板墙边振级大1～3 dB；厨房、卫生间较小跨度楼板中央竖向振级较墙边振级大0.3～2 dB；各房间跨中及墙边位置振动响应强度5层高于2层。

3.1.1.2 VAL振动加速度级分析

图9为地铁引起的SN2楼板中央及墙边Z向加速度振级随层高的变化。水平向振级随层高变化图略。图9中参量为边墙位置振级与楼板中央位置振级比值。由图9看出，竖向振级在高、低频段比值均小于1，仅中频段16～31.5 Hz范围内局部竖向振级比值大于1。

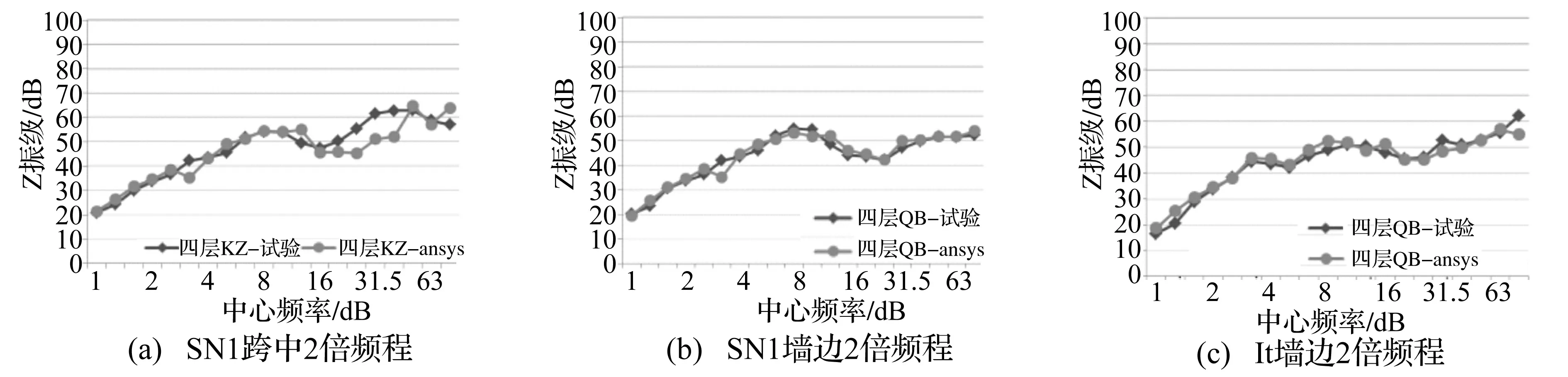
图7 计算值与实测值垂向加速度级

原因为墙边对楼板的约束作用导致边墙位置有局部共振效应，引起墙边位置在16～31.5 Hz中频段范围内振动强度大于跨中位置。总体趋势仍为跨中位置振动强度在各层均大于墙边位置振动强度，且随层高的增大，边墙与楼板中央位置比值越接近1，边墙振动强度越接近于楼板中央振动。统计数据显示，楼板中央竖向及水平向三向振级均大于边墙处振级，跨中与墙边最大差值见表3。由表3看出，竖向最大差值明显大于水平两向差值，且均出现于低层；而水平向最大差值较小，均出现于高层。

表3 不同房间跨中与墙边三方向振动数据最大差值(dB)

注：括号内数值为最大差值对应的中心频率

图8 2、5层不同房间跨中与边墙振动响应比较

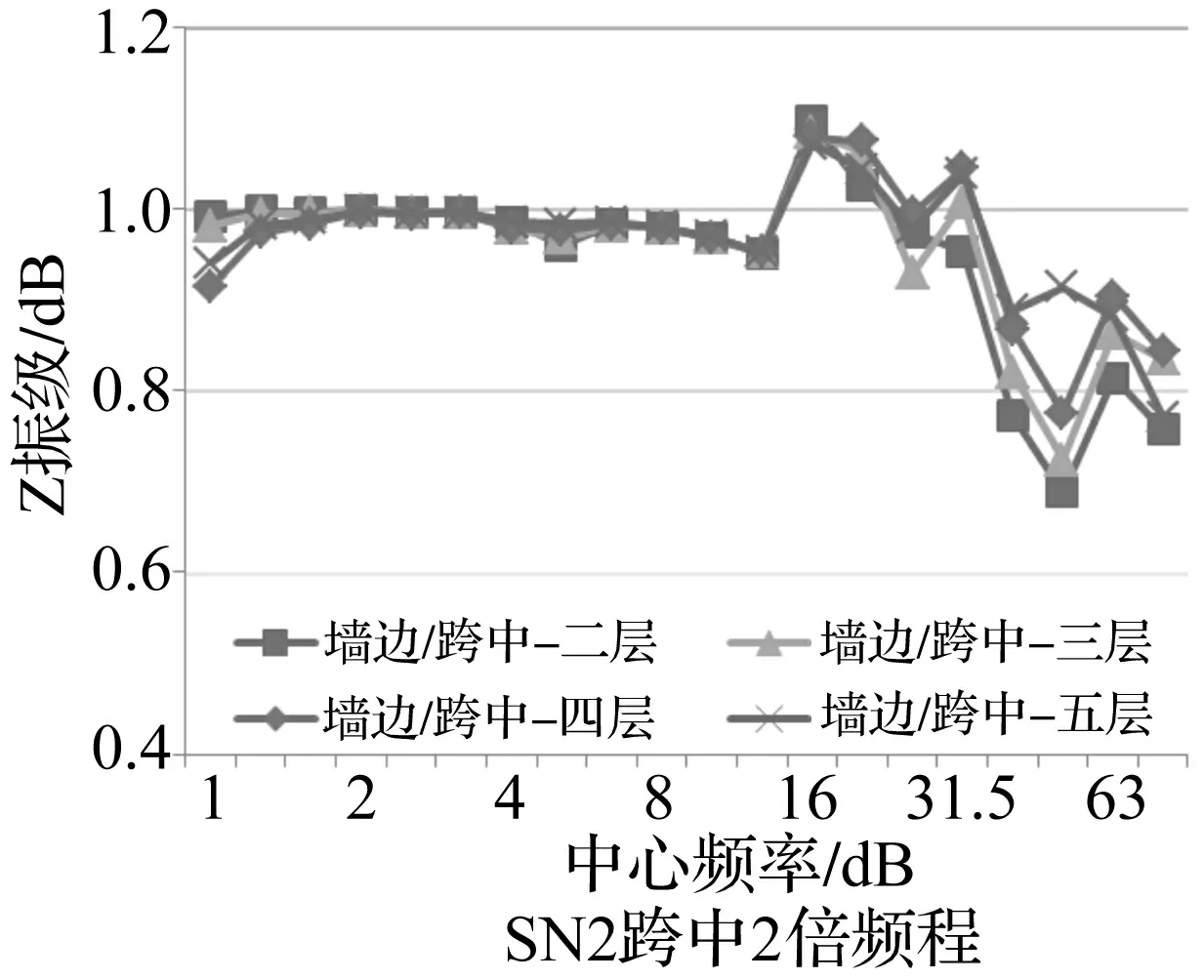
图9 楼板中央与墙边处Z向倍频程中心频率处振动加速度级随层高变化

3.1.2 预制板与现浇板对振动影响

年代较早楼房多采用预制板，因建筑功能需要，局部会用现浇板。本文所用两栋建筑属于该类型。为此，将预制板与现浇板分别按实际情况建立数值模型，此为深入分析楼板特性对振动影响较关键。试验建筑中，卫生间楼板为现浇板，其余房间均为预制板。为避免其它因素对楼板特性振动研究影响，选厨房间C3及卫生间W4，该两房型开间、进深与距地铁线路中心距离均一致或接近，两房间墙边约束均有一自由角，即角部影响接近。振动对比见图10。由图10看出，在各楼层竖向振级中：C3竖向振动较W4高0.5～1 dB，可见预制板对竖向振动有一定放大作用；而现浇板对竖向振动有一定衰减作用，原因主要为板材材质特性对振动影响，两种楼板自振频率因板材特性不同而不同，楼板自振频率与振动大小有关。而图10显示对振动强度影响较小。本文考虑简化模型，灰缝处理仅考虑在预制板布置方向墙边，故需分析灰缝对振动影响，见图11。预制板灰缝处(箭头指向)振动强度较无灰缝处理的预制板振动强度高2～3 dB，可见预制板间灰缝处对振动强度有一定放大作用，不容忽视；实际中预制板间均有灰缝，因此可推断实际结构中有预制板房间的竖向振动强度应大于现浇板房间。

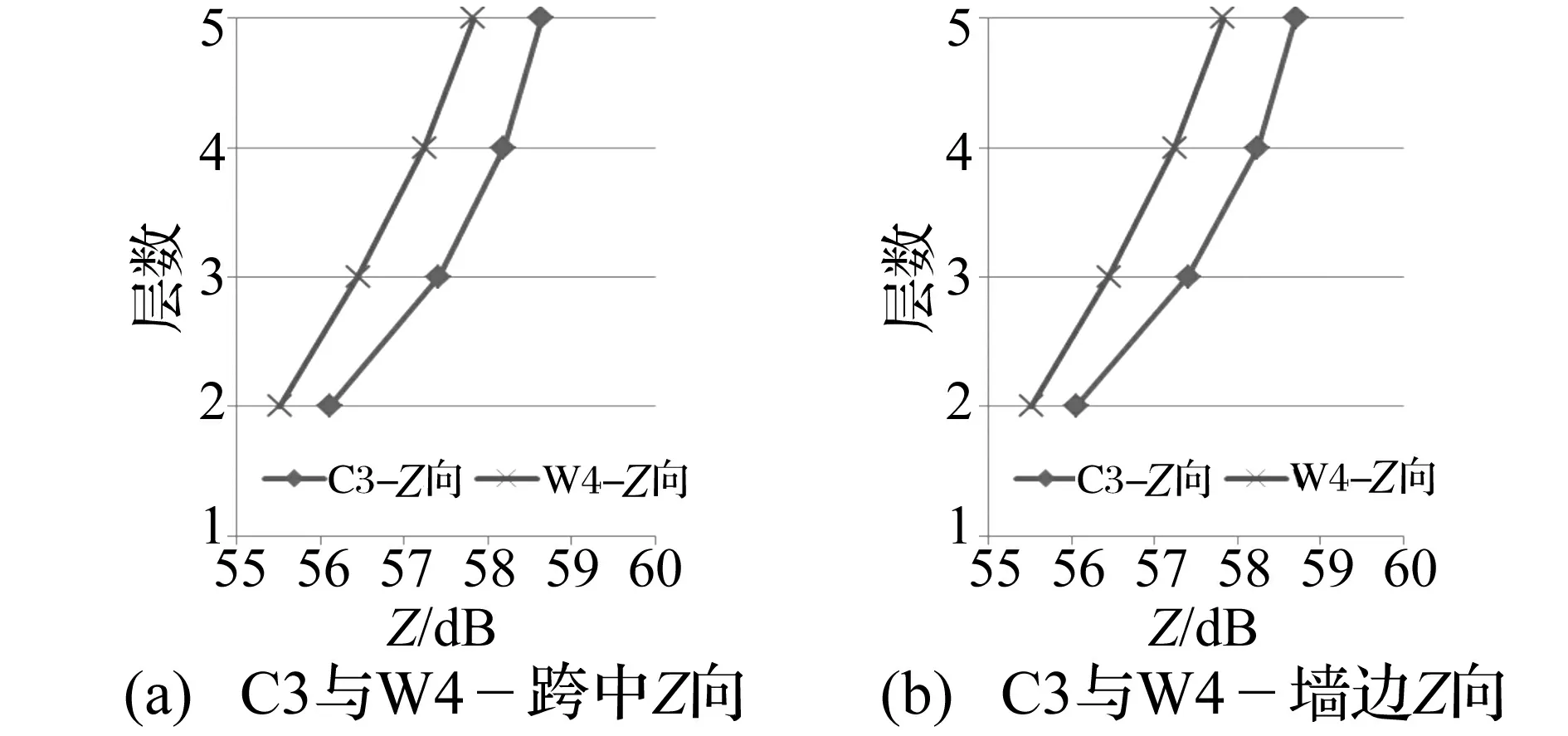
图10 厨房间与卫生间楼板中央及墙边处竖向振级随层高变化

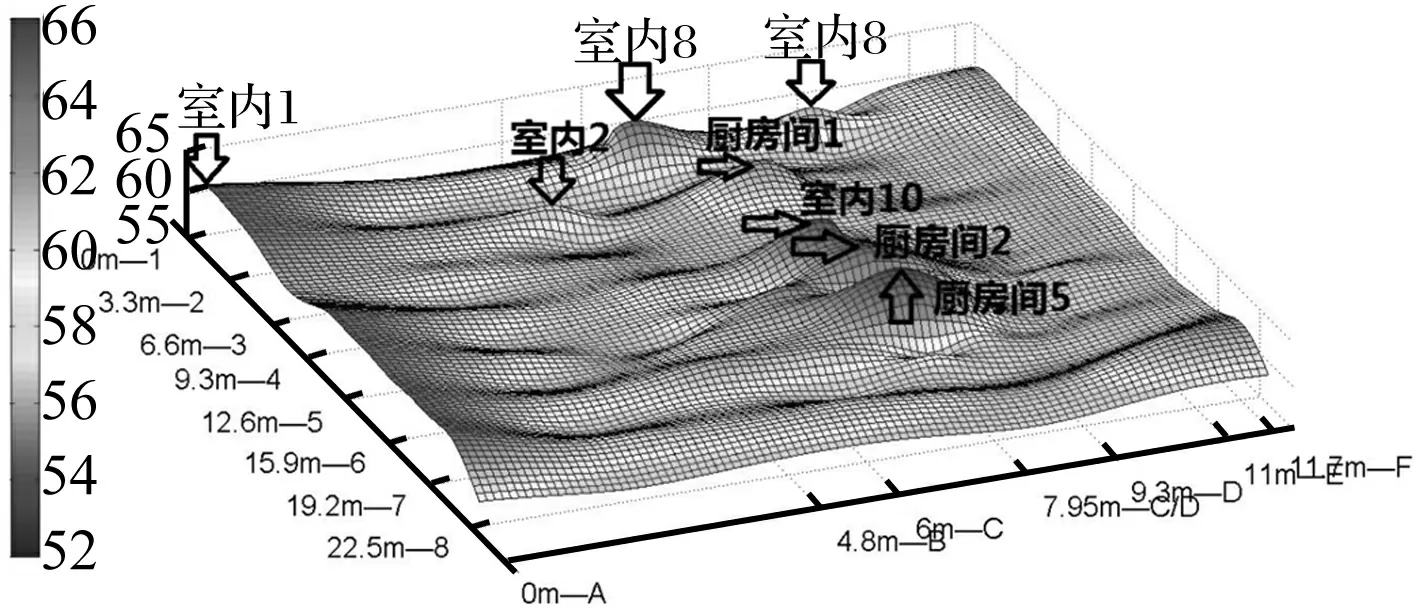
图11 某楼层全部房间竖向振动三维云图

3.1.3 房间进深、开间及墙边约束对振动影响

3.1.3.1 开间尺寸小于进深尺寸

为研究房间进深对振动影响大小，本文选其它参数基本一致而进深不同的SN7、SN9与C5、W9进行对比，SN7、SN9两间开间均3.3 m，进深分别为6 m、5 m，且两房型均两墙边受约束，一墙角部自由，见图12。为研究房间墙角部对振动影响大小，选SN1、SN8两房间开间均为3.3 m，进深分别为6 m、3.3 m，振动规律与SN7、SN9两房型一致,四个房型开间与进深大小与振动强度关系见表4。除Y向SN7与SN9振动强度基本一致外，Z向与X向振级在各层的振动强度SN7均大于SN9，差值见表5。由表5看出差值较小，且随层高增加而增大，最大值在顶层处仅1.5 dB，故进深参量越大，振动越强，但进深参量对振动强度影响较小，可忽略不计。

对比表4、表5看出，除二层Z向结果一致外，其余各层则相反，表明影响振动强度因素除开间、进深外，墙角约束也对振动强度有一定影响，见表6。由表6看出，SN9存在一自由墙角，其效应对振动有传递作用，起到对楼板振动衰减作用，而房间墙边约束较多易引起楼板的局部共振，对振动有局部放大作用，因此，振动强度与楼板周边约束关系较大。

图12 随层高变化SN7与SN9楼板中央三向振级比较

表4 四房型中不同参数对振动影响大小(dB)

3.1.3.2 开间尺寸大于进深尺寸

C5、W9两开间均为3.3 m，进深分别为3.15 m、2.4 m，约束相同，结果对比见图13。由图13看出，W9的竖向振动大于C5，而W9两水平向振动小于C5，表明进深尺寸小于开间尺寸时，进深越大，竖向振动越小，差值较小，最大值在四层为2.3 dB，而水平向振动则相反，进深越大，振动越大，但进深参量对振动强度影响较小，可忽略。

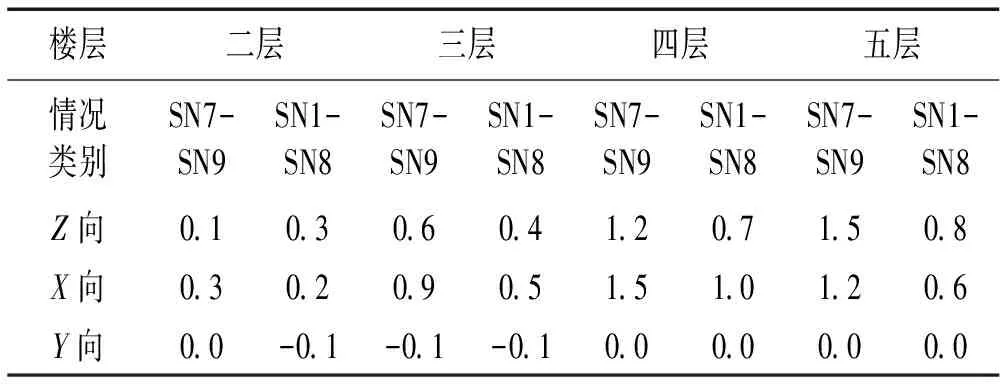
表5 不同进深房间三向振动数据差值(dB)

表6 四房型不同约束情况

注：图中正值表示W9振动强度大于C5

为研究房间开间对振动影响大小，选约束情况及其它参数基本一致、开间参数不同的C1、C5进行对比，结果见图14。由图14看出，进深3.15 m，开间分别为1.65 m、3.3 m，通过三向振级比较，得两房型中水平向振动强度大小一致，而竖向振级中C5振动强度明显高于C1，最大差值为顶层位置3.6 dB。因此，开间参数对水平向振动无明显影响，对竖向振动影响较大，开间越大，振动强度越大。图示15可直观看出两房型中开间大的C5振动强度大于开间小的C1。

3.2 同楼层内振动响应分布规律

基于既有结构振动分析研究，五层各房间振动三维云图见图16。由图16可清楚看出地铁经过楼房时各房间振动强度的分布。该三维云图不仅与3.1节数值结果吻合，且可观察除典型房间外其余各房间的振动情况。即振动强度大小及房间开间、进深、角部及边界情况、板材特性，楼层位置等因素有关；亦可直观对既有结构受地铁振动影响大小进行定性分析，为既有结构环境评估及隔振分析提供有力依据。

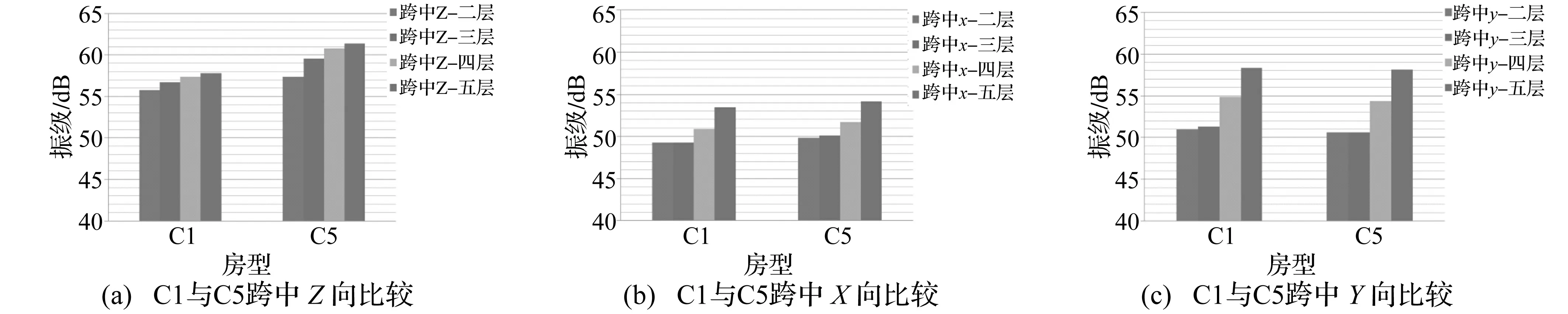
图14 随层高变化厨房1、5中楼板中央处三向振级比较

图15 某层全部房间竖向振动情况三维云图

4 结 论

通过对实验楼房所受振动的测量、数值模拟与分析，结论如下：

(1) 地铁通过时，大跨度室内位置楼板中央竖向振级较楼板墙边大1～3 dB；较小跨度楼板中央竖向振级较墙边大0.3～2 dB。

(2) 有预制板房间竖向振动强度大于现浇板房间；预制板灰缝处振动强度较无灰缝处理的预制板振动强度高2～3 dB，预制板间灰缝处对振动强度有一定放大作用。

(3) 进深尺寸大于开间尺寸时，进深参量越大，振动越强，进深参量对振动强度影响较小，可忽略；进深尺寸小于开间尺寸时，进深参量越大，竖向振动越小，水平向振动越大，但进深参量对振动强度影响较小，可不计；开间参数对竖向振动影响较大，开间越大，振动强度越大。

(4) 角部效应对振动有一定传递作用，可衰减楼板振动；而墙边约束较多房间易引起楼板局部共振，对振动有局部放大作用，振动强度与楼板周边约束有关。

(5) 边墙振动强度小于跨中位置振动强度。楼层越高，边墙振动强度越接近楼板中央振动。

(6) 由跨中与墙边最大差值对比知，竖向最大差值大于水平两向差值，出现于楼房低层；水平向最大差值较小，出现于高层。

参 考 文 献

[1]谢达文,刘维宁,刘卫丰,等. 地铁列车振动对沿线敏感建筑的影响预测[J]. 都市快轨交通, 2008,21(1):44-48.

XIE Da-wen, LIU Wei-ning,LIU Wei-feng, et al. Prediction of vibration impact of metro trains on adjacent sensitive buildings [J].Urban Rapid rail Transit, 2008, 21(1): 44-48.

[2]Gupta S, Liu W F, Degrande G, et al. Prediction of vibrations induced by underground railway traffic in Beijing[J]. Journal of Sound and Vibration, 2008, 310(3):608-630.

[3]Ding D Y, Gupta S, Liu W N, et al. Prediction of vibrations induced by trains on line 8 of Beijing metro[J]. Journal of Zhejiang University-Science A., 2010,11(4):208-293.

[4]马 蒙,刘维宁,丁德云. 地铁列车引起的振动对西安钟楼的影响[J]. 北京交通大学学报, 2010,34(4):88-92.

MA Meng, LIU Wei-ning, DING De-yun.Influence of metro train-induced vibration on Xi’an bell tower[J]. Journal of Beijing Jiaotong University,2010,34(4):88-92.

[5]钱春宇,郑建国,宋春雨. 西安钟楼台基受地铁运行振动响应的分析[J]. 世界地震工程, 2011,26(S1):177-181.

QIAN Chun-yu,ZHENG Jian-guo,SONG Chun-yu.Dynamic response analysis of bell tower foundation induced by train running on metro in Xi'an[J].World Earthquack Engineering,2011,26(S1):177-181.

[6]Breccolotti M, Materazzi A L, Salciarini D, et al. Vibrations induced by the new underground railway line in palermo, Italy-experimental measurements and FE modeling[C]// Proceedings of the 8th International Conference on Structural Dynamics(Eurodyn 2011)， Leuven, Belgium, 2011:719-726.

[7]Zhang N, Xia H, Yang W G, et al. Prediction and control of building vibration under metro excitations[C]// Proceedings of the 8th International Conference on Structural Dynamics(Eurodyn 2011), Leuven, Belgium, 2011:705-711.

[8]GB50203-2002,砌体工程施工及验收规范[S].

[9]GB50068-2001,建筑结构可靠度设计统一标准[S].

[10]Chopra A K,著.谢礼立,译.结构动力学：理论及其在地震工程中的应用[M].北京：高等教育出版社,2005.

[11]王田友.地铁运行所致环境振动与建筑物隔振方法研究[D].上海:同济大学，2007.

[12]Hanazato T, Ugai K, Mori M, et al. Three-dimensional analysis of traffic-induced ground vibrations[J].Journal of Geotechnical Engineering,1991,117(8):1133-1151.

[13]Chua K H, Lo K W, Balendra T. Building response due to subway train traffic[J]. Journal of Geotechnical Engineering, 1995, 121(11):747-754.