基于矩阵分式多项式时变结构模态参数最小二乘辨识

周思达， 刘 莉， 杨 武， 马志赛

(北京理工大学 宇航学院，北京 100081)

由于传统结构动力学研究中，通常假设被分析结构为时不变，故使结构动力学研究的诸多成果成功运用于工程结构分析、设计中。然而随工程结构应用领域的不断拓展，尤其航空航天、机械、桥梁等应用领域，越来越多结构随时间变化特性不可忽略[1]。如铁路桥与火车形成的组合结构系统，火车通过时的运动导致组合结构系统质量分布会发生改变[2-3]，甚至导致结构阻尼、刚度的改变[4]；制造业中机械臂在完成不同动作时几何特征会发生变化，导致其结构动力学特性产生相应变化[5-6]；人与运动场形成的组合系统，运动场处于不同状态时，无比赛时场地空置、比赛前观众入场、比赛进行等，人与运动场组合系统的结构特性随时间变化，此在运动场结构健康监测中亦不可忽略[7]。

模态分析中模态参数辨识已广泛应用于结构动力学研究与应用。如结构健康监测、故障诊断、模型更新、强迫振动分析等[8]。因此，进行线性时变结构的模态参数辨识研究十分必要。

在线性时变系统理论及系统辨识理论研究发展推动下，线性时变结构模态参数辨识研究亦在发展。现有时变结构模态参数辨识方法主要分两类，即参数化时域辨识方法与非参数化时频域辨识方法。参数化时域辨识方法中亦分两类：①基于时间相关自回归滑动平均模型(TARMA)，如Poulimenos等[9]的泛函序列TARMA(FS-TARMA)方法；②基于状态空间模型，如Liu[10]将传统子空间方法(SSI)拓展到时变结构。吴日强等[11-12]提出改进递推子空间方法；杨利芳等[13]对几种用于时变结构模态参数辨识子空间方法进行比较研究。非参数化时频域辨识方法为基于时频分析的时变结构模态参数辨识方法，通过对时变结构响应信号进行时频分析识别出目标结构相关模态参数，如Ghane等[14]提出基于小波变换的模态参数辨识方法；许鑫等[15]提出基于连续小波变化的线性时变结构瞬时频率辨识方法；Roshan-Ghias等[16]提出基于平滑伪Wigner-Ville分布的辨识方法；续秀忠等[17-18]利用Gabor展开及Wigner-Ville分布辨识时变结构模态频率；王学敏[19]提出基于Hilbert-Huang变换(HHT)的线性时变结构模态频率辨识方法；Feldman[20]提出基于Hilbert振动分解(HVD)的时变结构模态参数辨识方法。

本文在现有针对时不变结构参数化最小二乘复频域方法基础上，将其拓展到时频域，提出参数化时频域模态参数辨识方法，其中参数化模型为时间相关的矩阵分式多项式模型，参数估计方法为最小二乘方法，并通过仿真算例验证所提方法的有效性。本文时变结构模态参数最小二乘辨识方法由三部分组成：①建立时间相关矩阵分式多项式形式的时变结构动力学参数化模型，包括模型阶数等，即时间与频率多项式阶数；②构建时频域最小二乘参数估计方法，估计出时变结构参数化动力学模型中待估参数；③据所得待估参数，求解时变结构模态参数。

1 时间相关矩阵分式多项式模型

结构动力学系统频率响应函数可表示为矩阵分式多项式形式：

(1)

其中：B(ω)为分子矩阵多项式；A(ω)为公分母多项式。

GXX(ω)=H(ω)GFF(ω)GH(ω)

(2)

其中：H(ω)为结构频率响应函数矩阵；GFF(ω)为激励(输入)信号功率谱函数矩阵；GXX(ω)为结构响应(输出)信号功率谱函数矩阵。

对仅输出模态参数辨识而言，设作用于结构的激励为白噪声，结构响应功率谱函数输入信号功率谱函数矩阵GFF(ω)为关于频率的常数矩阵。则结构响应信号功率谱函数仅为结构参数(如刚度、阻尼系数、质量)的函数，也可写为式(1)的矩阵分式形式。据Zadeh[21]关于线性时变系统频域表示，慢时变系统仍可近似表示为分式多项式形式。因此，本文将时不变结构功率谱函数矩阵分式多项式模型拓展为时间相关的矩阵分式多项式模型，以表示时变结构时间相关功率谱函数(输出o及参考点i)，定义为：

(3)

其中：下标τ=1,2,…,N为时间采样；f=1,2,…,Nf为频率采样；k=1,2,…,NoNi(即k=(i-1)No+o)，No与Ni分别为输出数及参考点数，分子多项式与公分母多项式分别定义为：

(4)

(5)

其中：φi,j(t,ω)为时频基函数(时间多项式及频率多项式分别为i，j阶，i=0,1,m2,…,nt，j=0,1,2,…,nω)；多项式系数bk,i,j及ai,j可写为向量形式：

(6)

(7)

为方便推导，将式(7)参数向量写为：

(8)

其中：θ为参数化矩阵分式多项式模型待定参数向量。

2 时频域最小二乘辨识方法

提出时频域最小二乘方法，对式(3)线性时变结构参数化模型进行参数估计，获得待定参数向量θ，并通过θ获得结构时变模态参数。

2.1 最小二乘问题

据时频域时变结构动力学参数化时间相关矩阵分式多项式模型(式(3))，时频域线性最小二乘费用函数定义为：

(9)

其中：θ为式(8)的待定参数向量，方程误差为：

(10)

由式(4)～式(8)，方程误差可写成矩阵形式，为：

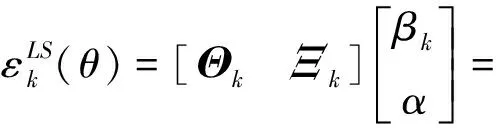
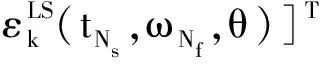
(11)

其中：

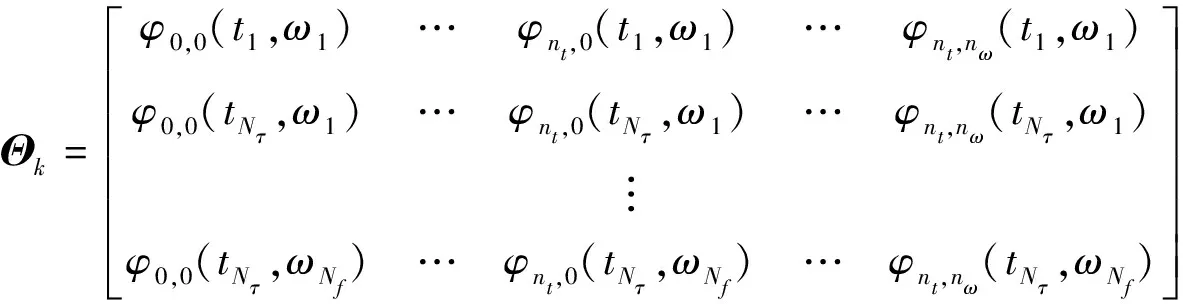
据矩阵形式定义方程误差(式(11))，时频域线性最小二乘费用函数(式(9))可写为：

(12)

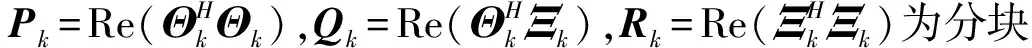
考虑最小二乘中Jacobi矩阵分块矩阵，式(12)可表示为：

ϑLS(θ)=θTRe(JHJ)θ

(13)

其中：

2.2 基于减缩正则方程最小二乘求解

为求解式(13)最小二乘问题，采用基于缩减正则方程方法求解。当式(9)费用函数取最小值时，其对待定参数导数为零，即：

(14)

(15)

将式(14)代入式(15)，得：

(16)

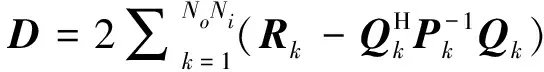
式(13)参数化模型具有参数冗余，给定常数γ，有：

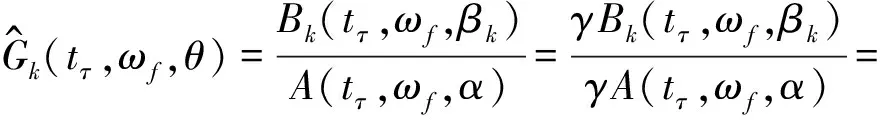
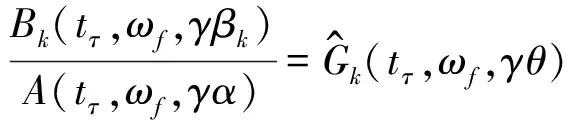
(17)

式(17)的参数冗余会使缩减的最小二乘正则方程右端项为0，导致方程只有平凡解或无穷多解。因此，须对模型参数施加约束，选α中任意一分量设为常数1，则缩减的正则方程为：

D′α′=b′

(18)

其中：

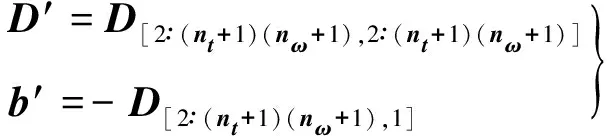
或

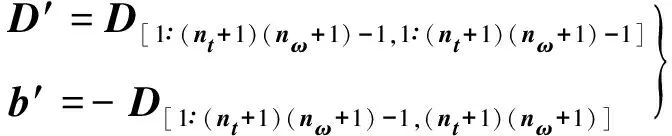
对α中不同分量施加约束，会引起辨识结果包含不同情况的稳定极点与不稳定极点，文献[22]给出关于时不变结构相关辨识的详细分析与结论。本文将利用解析算例对该内容进行详细讨论。

3 求解模态参数

通过线性最小二乘辨识可得参数化模型(式(3))中待估的未知参数向量θ。若θ确定，则时间相关功率谱函数矩阵分式多项式模型确定。将矩阵分式多项式模型转换为极点-留数模型可得结构模态参数：

(1) 通过求解含系数α的各时刻公分母多项式A(t,ω,α)的根获得系统极点，再利用系统极点获得结构模态频率及模态阻尼比：

(19)

其中：fr(t)为t时刻结构模态频率；ξr(t)为结构模态阻尼比。

(2) 据所得系统极点与参数化功率谱函数获得系统留数：

(20)

(3) 通过留数矩阵计算工作模态参数向量(无缩放的结构模态振型)[23]：对留数矩阵进行奇异值分解(SVD)获得酉矩阵U第一列即工作模态参数向量：

Rr=U∑V

(21)

4 算例一

为考察本文所提线性时变结构模态参数辨识方法性能与待估参数约束对辨识结果影响，给出解析表达功率谱函数算例。

4.1 算例设置

三自由度弹簧-阻尼-质量系统见图1。其中质量随时间变化，质量矩阵为：

(22)

其中：tend=1 s为终止时刻；pc=0.5为比例系数；M0为初始时刻质量矩阵。

图1 三自由度弹簧-阻尼-质量系统

设激励为理想白噪声，系统响应功率谱函数仅为结构参数函数。据给定系统参数可直接获得此系统解析的无噪声时间相关功率谱函数，第一、二自由度响应互功率谱函数见图2(限于篇幅，仅给出G12)。

图2 解析的无噪声时间相关功率谱函数(G12)

4.2 辨识结果

以图1的解析时间相关功率谱函数(包含G11，G12，G13)为测量值，采用所提线性时变结构模态参数最小二乘辨识方法进行模态参数辨识，获得辨识的时间相关功率谱函数，其中第一、二自由度响应互功率谱函数见图3。辨识所得时变模态频率及模态阻尼比见图4(圆圈为理论值，实线为辨识结果)。

由图3、图4看出，所提线性时变结构模态参数最小二乘辨识方法能十分准确的辨识出无噪声功率谱情况下时变结构模态参数，且辨识结果不依赖待估参数的约束。图1的解析时间相关无噪声功率谱函数上叠加高斯白噪声，获得信噪比10 dB有噪声情况下时间相关功率谱。0.25 s时刻有噪声时间相关功率谱见图5(其中实线为无噪声，点为有噪声)。

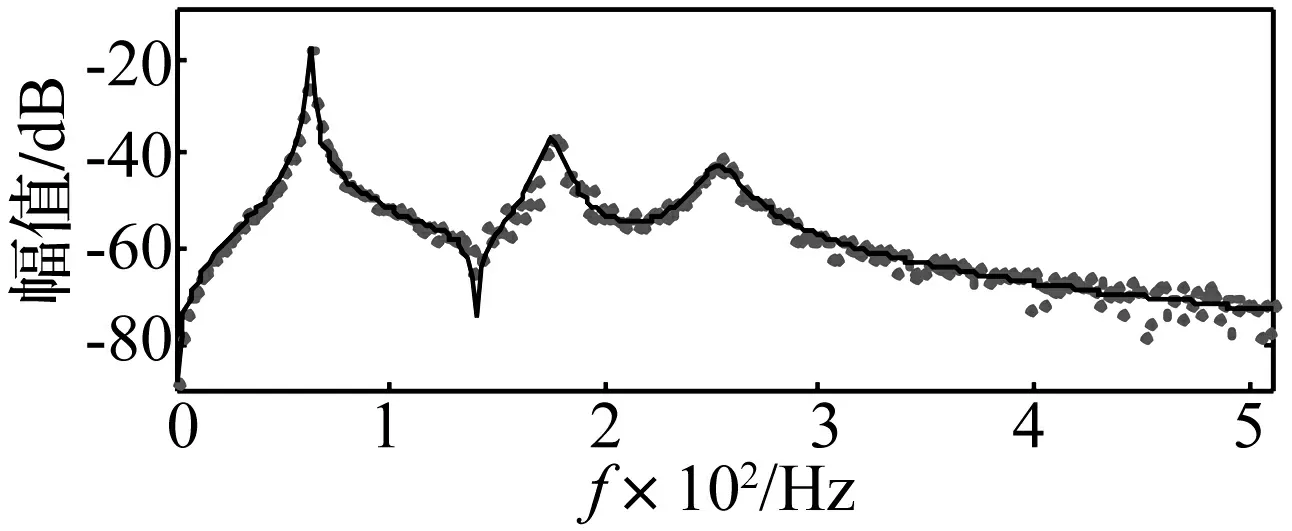
图5 解析的有噪声时间相关功率谱函数(有噪声，G12)

图6 辨识所得时间相关功率谱函数(有噪声，G^12)

以上所述有噪声时间相关功率谱为测量值，采用所提辨识方法进行模态参数辨识。分别施加式(18)两种待估参数约束，辨识获得时间相关功率谱函数见图6。辨识所得模态频率及阻尼比见图7。

由以上辨识结果可知，有噪声时α的不同约束方式对辨识结果影响较大。原因为对α的不同约束对辨识所得稳定极点、不稳定极点的分布产生影响，即在约束时不稳定极点被视作稳定极点。而无噪声时，稳定极点与不稳定极点成对出现，即将不稳定极点视为稳定极点亦不影响结果。所提方法具有的此性质与用于时不变结构模态参数辨识的最小二乘复频域法相关性质[22]类似。若给定正确约束(式(18)的约束二)，所提线性时变结构模态参数最小二乘辨识方法能较好辨识出有噪声时线性时变结构模态频率及模态阻尼比。

5 算例二

实际工程应用中结构响应时间相关功率谱函数无法直接测量或通过解析方式获得。因此通过数值积分求解响应仿真算例进一步验证所提线性时变结构模态参数最小二乘辨识方法。由于激励是随机的且响应由数值积分直接求得，因此本算例考虑输入噪声。所用时变系统与算例一类似，仍为三自由度弹簧-阻尼-质量时变系统，质量随时间按线性关系减少，即：

M(t)=M0(1-pct/tend)

(23)

其中：tend=1 s为终止时刻；pc=0.5为比例系数。

给定激励为作用在系统第一自由度的仿真高斯白噪声。系统响应采用Newmark-β数值积分方法[24]计算获得，其中积分步长为1/4 096 s。响应信号采样频率1 024 Hz，采样时间1 s。采用SPWVD非参数化估计时间相关功率谱函数，平均次数40次。由平滑伪Wigner-Ville分布(SPWVD)[25]非参数化估计的第一、二、三自由度响应时间相关互功率谱函数见图8。

图8 SPWVD非参数化估计时间相关功率谱函数(G12，G13)

图10 辨识所得时变模态参数

以上仿真算例表明，所提线性时变结构模态参数最小二乘辨识方法能在仅输出情况下较好辨识出线性时变结构的模态频率，但由于阻尼辨识本身困难及最小二乘辨识未考虑测量值的不确定性，阻尼辨识结果不及模态频率好，尤其第一、三阶模态阻尼比与理论值有一定偏差。

6 结 论

(1) 本文所提基于矩阵分式多项式模型的线性时变结构模态参数最小二乘辨识方法，给出线性时变结构时频域参数化模型-时间相关矩阵分式多项式模型；所提模态参数最小二乘辨识方法，其中基于缩减正则方程的最小二乘求解方法大大降低对计算资源要求。

(2) 通过解析算例验证所提线性时变结构模态参数最小二乘辨识方法中待估参数约束对辨识结果影响，指出正确约束方式。并在仅输出条件下较好辨识出线性时变结构模态频率，方法的有效性获得验证。

参 考 文 献

[1]邹经湘, 于开平, 杨炳渊. 时变结构的参数识别方法[J]. 力学进展, 2000, 30(3): 370-377.

ZOU Jing-xiang,YU Kai-ping,YANG Bing-yuan. Methods of time-varying structural parameter identification[J]. Advances In Mechanics, 2000, 30(3): 370-377.

[2]Au F T K, Jiang R J, Cheung Y K. Parameter identification of vehicles moving on continuous bridges[J]. Journal of Sound and Vibration, 2004, 269(1-2): 91-111.

[3]Marchesiello S, Bedaoui S, Garibaldi L, et al. Time-dependent identification of a bridge-like structure with crossing loads[J]. Mechanical Systems and Signal Processing,2009,23(6):2019- 2028.

[4]Jiang R J, Au F T K, Cheung Y K. Identification of vehicles moving on continuous bridges with rough surface [J]. Journal of Sound and Vibration, 2004, 274(3-5): 1045-1063.

[5]Kopmaz O, Anderson K S. On the eigenfrequencies of a flexible arm driven by a flexible shaft[J]. Journal of Sound and Vibration, 2001, 240(4): 679-704.

[6]Chang P H, Park H S. Time-varying input shaping technique applied to vibration reduction of an industrial robot[J]. Control Engineering Practice, 2005, 13(1): 121-130.

[7]Peeters B, Van Der Auweraer H, Vanhollebeke F, et al. Operational modal analysis for estimating the dynamic properties of a stadium structure during a football game[J]. Shock and Vibration, 2007, 14(4): 283-303.

[8]Heylen W, Lammens S, Sas P. Modal analysis theory and testing [M]. Leuven: Katholieke Universiteit Leuven, 2007.

[9]Poulimenos A G, Fassois S D. Output-only stochastic identification of a time-varying structure via functional series TARMA models[J]. Mechanical Systems and Signal Processing, 2009, 23(4): 1180-1204.

[10]LIU K. Identification of linear time-varying systems[J]. Journal of Sound and Vibration, 1997, 206(4): 487-505.

[11]吴日强, 于开平, 邹经湘. 改进的子空间方法及其在时变结构参数辨识中的应用[J]. 工程力学,2002,19(4): 67-70,89.

WU Ri-qiang, YU Kai-ping, ZOU Jing-xiang. An improved subspace method and its application to parameter identification of time-varying structures[J]. Engineering Mechanics, 2002, 19(4): 67-70,89.

[12]庞世伟, 于开平, 邹经湘. 用于时变结构模态参数识别的投影估计递推子空间方法[J].工程力学,2005,22(5):115-119.

PANG Shi-wei,YU Kai-ping,ZOU Jing-xiang. A projection approximation recursive subspace method for identification of modal parameters of time-varying structures[J]. Engineering Mechanics, 2005, 22(5): 115-119.

[13]杨利芳, 于开平, 庞世伟,等. 用于线性时变结构系统辨识的子空间方法比较研究[J]. 振动与冲击,2007,26(3):8-12, 153.

YANG Li-fang,YU Kai-ping, PANG Shi-wei, et al. Comparison study on identification methods applied to linear time-varying structures[J]. Journal of Vibration and Shock, 2007, 26(3): 8-12,153.

[14]Ghanem R, Romeo F. A wavelet-based approach for the identification of linear time-varying dynamical systems[J]. Journal of Sound and Vibration, 2000, 234(4): 555-576.

[15]许 鑫,史治宇,Wieslaw J. Staszewski,等.基于加速度响应连续小波变换的线性时变结构瞬时频率识别[J].振动与冲击, 2012,31(20):166-171.

XU Xin,SHI Zhi-yu, Staszewski W J, et al.Instantaneous frequnencies identification of a linear time-varying structure using continuous wavelet transformation of free decay acceleration response[J].Journal of Vibration and Shock, 2012, 31(20):166-171.

[16]Roshan-ghias A, Shamsollahi M B, Mobed M, et al. Estimation of modal parameters using bilinear joint time-frequency distributions[J]. Mechanical Systems and Signal Processing, 2007, 21(5): 2125-2136.

[17]续秀忠,张志谊,华宏星,等. 结构时变模态参数辨识的时频分析方法[J]. 上海交通大学学报, 2003, 37(1): 122-126.

XU Xiu-zhong, ZHANG Zhi-yi, HUA Hong-xing, et al. Time-varying modal parameter identification with time-frequency analysis methods[J]. Journal of Shanghai Jiaotong University, 2003, 37(1): 122-126.

[18]续秀忠, 华宏星, 张志谊,等. 应用时频表示进行结构时变模态频率辨识[J]. 振动与冲击, 2002, 21(2): 36-40,44.

XU Xiu-zhong, HUA Hong-xing, ZHANG Zhi-yi, et al. Time-varying modal frequency identification by using time-frequency representation [J]. Journal of Vibration and Shock, 2002, 21(2): 36-40,44.

[19]王学敏. 基于Hilbert-Huang变换的桥梁监测信号分析与处理和时变模态参数识别[D]. 长沙:中南大学, 2008.

[20]Feldman M. Time-varying vibration decomposition and analysis based on the Hilbert transform [J]. Journal of Sound and Vibration, 2006, 295(3-5): 518-530.

[21]Zadeh L A. Frequency analysis of variable networks[J]. Proceedings of the IRE, 1950, 38(3): 291-299.

[22]Cauberghe B, Guillaume P, Verboven P, et al. On the influence of the parameter constraint on the stability of the poles and the discrimination capabilities of the stabilisation diagrams[J]. Mechanical Systems and Signal Processing,2005,19(5): 989-1014.

[23]Verboven P. Frequency-domain system identification for modal analysis [D]. Brussels:Vrije Universiteit Brussel, 2002.

[24]Newmark N M. A method of computation for structural dynamics [J]. Journal of Engineering Mechanics, ASCE, 1959, 85(7): 67-94.

[25]Qian S. Introduction to time-frequency and wavelet transforms [M]. Prentice Hall, 2002.