非线性涡激力模型气动参数识别新方法

翁祥颖， 葛耀君， 陈海兴

(同济大学 土木工程防灾国家重点实验室，上海 200092)

流经钝体断面的流体在钝体下游表面形成漩涡且有规律脱落引起的物体振动称涡振。涡振为典型的限幅自激振动，由于Van der Pol 振子具有类似特性，现有桥梁涡振单自由度涡激力模型均基于Van der Pol振子构造而成。此模型均含与振动系统折算频率相关的气动参数，使用该模型时需据风洞试验结果识别系统的涡激力参数。Ehsan等[1]通过赋予处于涡振状态的节段模型大于其涡振振幅初位移并测量模型振动衰减时程以确定模型中与非线性阻尼项相关的气动参数，识别时直接假定涡振为简单简谐振动。而该简谐振动并非基于非线性涡激力模型结构涡振运动平衡方程的解，该假定与方程解析解间的较大差别必对涡激力模型气动参数识别结果产生影响。Gupta[2]基于不变嵌入理论提出非线性最小二乘识别法。对不同初始值该方法会获得不同结果甚至拟合不收敛，但并未就如何正确设定初始值给出建议。Marra等[3-4]基于缓变参数法亦提出涡激力参数识别方法，然而在将识别的气动参数代入涡激力模型并反算节段模型响应时发现反算响应功率谱与实测相比除涡脱频率外出现一额外卓越频率。另外，以上识别方法其本质均为非线性最小二乘法，当给拟合目标设定不同初始值时，拟合所得结果亦不同，不便于研究及应用。对此，本文基于遗传算法提出具有较高稳定性的非线性单自由度涡激力气动参数识别方法。

1 单自由度经验非线性涡激力模型

该模型由Scanlan[5]提出，因其具有较高精度而在桥梁涡振研究中广泛应用。基于Van der Pol振子，该模型由含非线性效应的气动阻尼、气动刚度自激力及瞬时简谐强迫力共同构成：

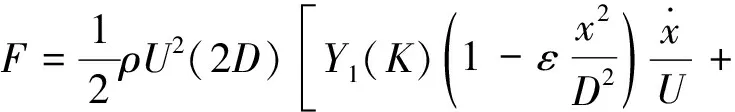
(1)

定义无量纲量：

(3)

式中：m为系统每米模态质量。

结合简化的涡激力模型得涡振运动平衡微分方程的无量纲形式为：

(4)

其中：

μ1=-[2ξKn-mrY1(K)]

(5)

μ2=mrY1(K)ε

(6)

(7)

式中：ξ为系统阻尼比。显然，式(4)描述的系统振动特性与μ1，μ2密切相关：μ1，μ2符号相反时，系统会发生衰减或发散振动，不符合涡振发生时结构呈等幅振动特性。由涡振为稳定的等幅振动知μ1为正数，故定义变量：

(8)

代入以上无量纲涡振运动平衡微分方程可得标准的Van der Pol振子为：

(9)

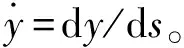
2 Van der Pol振子近似解

Van der Pol振子含非线性阻尼项，其精确的闭合解析解目前仍难以获得。传统的近似求解方法包括KBM法、谐波平衡法等均要求振子中阻尼系数μ1为接近于零的小参数。对涡振而言，由于μ1与气动参数直接相关，无法先了解其大小，因而无法保证传统解法是否适用。为此本文采用不依赖小参数的近似级数求解方法-同伦分析法(Homotopy Analysis Method)[6]。该法求解非线性微分方程核心为在方程未知量中引入控制参数p，使未知量变为含p的多元函数，p由0变到1的过程中，未知量则由微分方程对应的线性方程解变到原始的非线性微分方程解。

为满足同伦分析法要求各未知量相对于控制参数p求各阶导数条件，需先将式(9)中两未知量-频率Kn及振动幅值a由隐式变为显式，为此定义变量为：

τ=ωs,y(s)=au(τ)

(10)

代入式(9)得适用于同伦分析法的基本方程为：

ω2u″(τ)+μ3u(τ)=μ1ω[1-a2u2(τ)]u′(τ)

(11)

由同伦分析法得Van der Pol振子二阶近似解为：

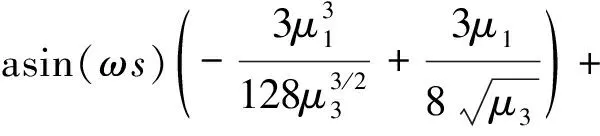
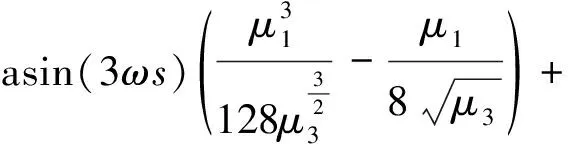
(12)

(13)

(14)

重复以上过程，可得更高阶近似解。但三阶以上的解是关于频率大于等于7ωn的高频成分，考虑桥梁节段模型涡振响应主导振动频率较单一，二阶近似解已能较好反映出振动特性。

3 拟合目标函数

结合风洞试验实测桥梁节段模型涡振响应时程及所得二阶近似解，构造表示残差平方和的拟合目标函数为：

(15)

式中：ym(s)，ye(μ1,μ3,s)为实测涡振响应与计算所得响应；s为无量纲时间；N为位移响应时程样本容量。

4 遗传算法识别参数

对非线性拟合问题，传统方法如牛顿法、拟牛顿法、梯度下降法等与梯度相关的拟合方法给出的拟合结果往往只是所给初始值附近局部极值，无法识别定义域范围内全局最优值，故此方法识别结果与拟合目标初始值设定直接相关，不便于研究及应用。为克服该缺陷，采用旨在搜索全局最优值的启发式拟合法-遗传算法，该算法主要思想为模拟自然界生物优胜劣汰的进化规律。拟合对象取值范围及拟合目标函数一旦确定，遗传算法则通过既定的遗传策略，如种群数量、选择、交叉、变异等操作，产生代表更优解的下一代个体直至收敛获得最终拟合值[7]。

基于此拟合思路，编制拟合μ1，μ3的遗传算法程序。考虑试验中实测响应信号均含随机噪声，本文分别采用光滑及含高斯白噪声的有噪位移时程信号验证所提方法的可行性及程序编制的正确性。针对涡振发生时桥梁节段模型发生较大、规则的限幅自激振动，采集的振动信号较光滑，故设置有噪信号的噪信比为2.0%。数值验证中原始光滑信号在参数μ1=0.70，μ3=1 280条件下数值积分由式(9)获得。遗传算法其它参数设置：种群个体数M=50，交叉概率Pc=0.7，个体变异概率Pm=0.05，最大迭代次数N=300；参数μ1，μ3的搜索范围分别为[0,1]、[302,402]；采用线性排序结合精英选择的混合选择策略。两种数值模拟试验均进行30次以观察识别结果的稳定性。对光滑位移时程信号，各次识别结果变化较小且均接近于μ1，μ3目标值，最终识别结果为μ1=0.708 4,μ3=1 279.99。对有噪的位移时程信号，各次试验识别的μ3很稳定，最大误差仅0.3%；但μ1相对较离散。观察并统计识别结果发现，μ3微量差别引起的相位差使识别结果残差平方和变化剧烈并导致μ1识别结果较离散。为此进行两轮识别：第一轮同时识别μ1及μ3，因μ3较稳定故先确定μ3；第二轮仅识别μ1，将μ3视为已知数以消除识别过程中相位差再次变化对μ1识别产生的剧烈影响。

图1 原始有噪位移时程与拟合结果对比

由于加入高斯白噪声，有噪信号识别结果稳定性不及光滑信号，达到搜索停止条件时种群多样性有时仍较大，因而搜索到最优解难度、时间随之增加。统计30次识别结果，据残差平方和最小原则可确定本次数值验证进行30次试验中最优识别结果为μ1=0.704,μ3=1 280.00，与目标值基本一致。图1为原始有噪位移时程与据识别结果计算所得位移时程。由图1看出，两者吻合较好。

5 桥梁节段模型涡激力气动参数识别

5.1 风洞试验概况

试验在同济大学TJ-3风洞进行。图2为风洞试验节段模型所用流线型闭口箱梁断面。箱梁节段模型宽2D=0.553 m，一阶竖弯模态质量M=10.1 kg/m，频率f=5.664 Hz，系统阻尼比ξ=1.25%。均匀流场中风速U=6.0 m/s时节段模型出现稳定竖弯涡振。试验系统见图3。图4为无量纲的竖弯涡振位移时程。对应于该锁定风速，系统折算频率Kn=3.221。试验中用两个采样频率100 Hz的激光位移计测量节段模型位移时程。

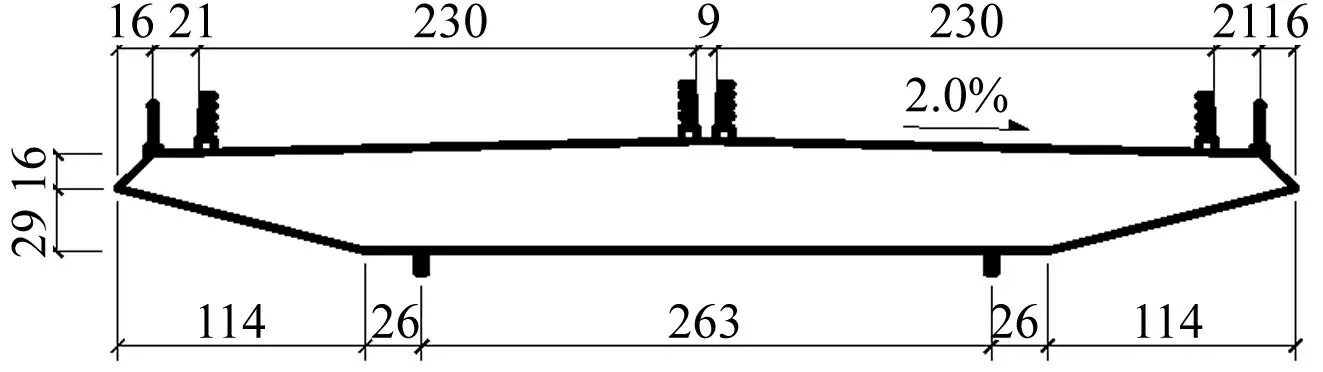
图2 涡振试验主梁节段模型流线型断面

图3 试验系统

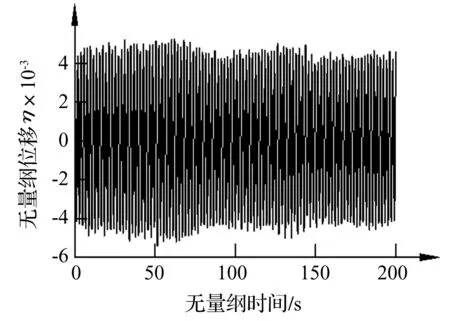
图4 无量纲的竖弯涡振响应时程

5.2 μ1，μ3参数搜索

结合式(8)、(13)，得无量纲实测涡振与Van der Pol振子位移幅值间关系为：

(17)

其中：At为无量纲实测竖弯涡振位移响应幅值。该比值可通过迭代法确定，初始值分子取2。

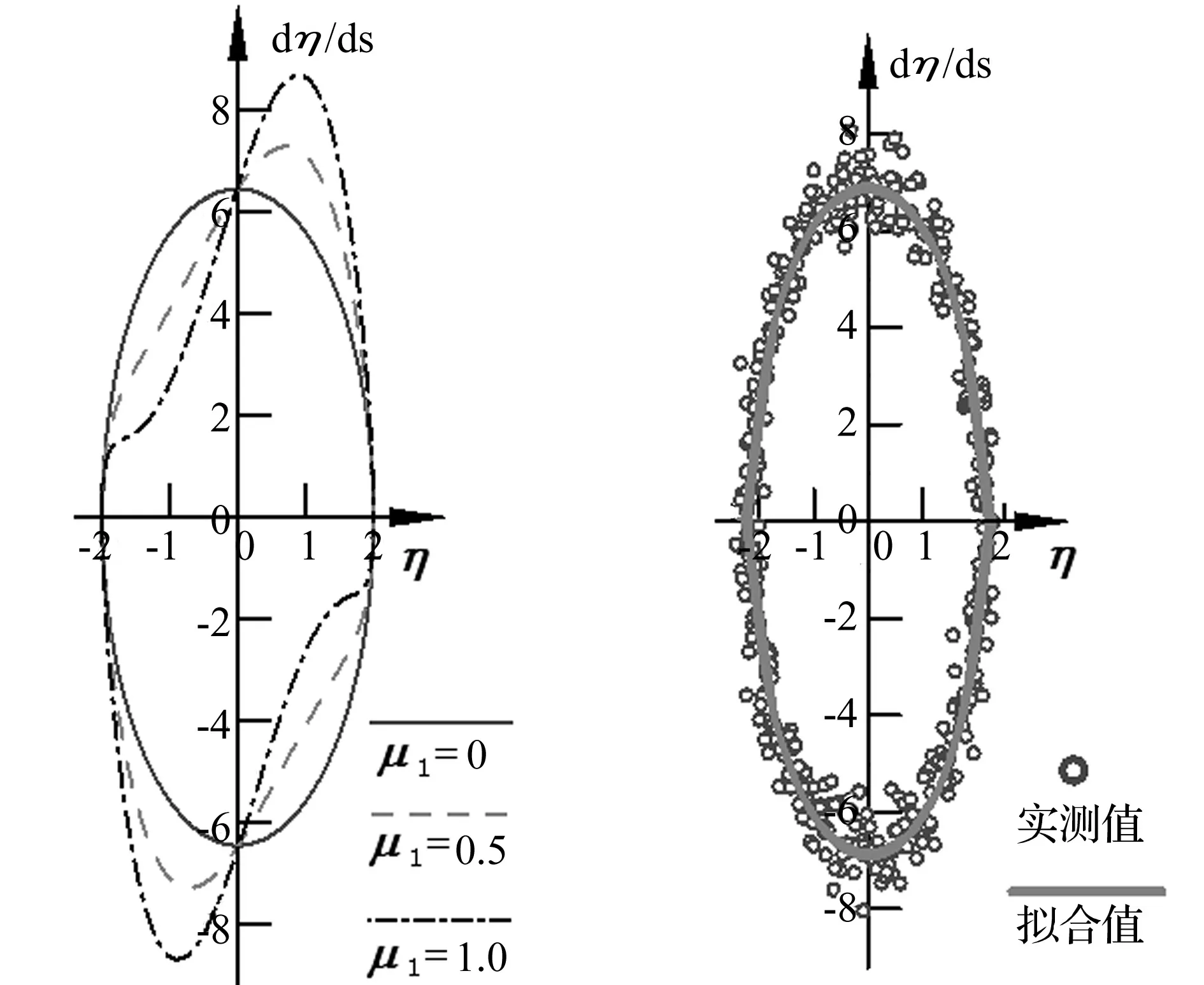
图5 极限环与拟合限幅环

桥梁节段模型发生涡振时系统振动频率与零风速时固有频率相比变化较小，因而确定μ3的搜索范围为[33,42]。由于Van der Pol振子在相空间内为限幅环运动，随μ1的改变，限幅环形状亦发生变化。利用此对应关系可初步确定μ1搜索范围。图5(a)对应μ1=0,0.5,1三个不同值限幅环[8]。图5(b)为由实测竖弯涡振响应拟合所得限幅环，发现其长轴方向与y轴偏差很小。对比图5(a)结果，确定μ1的搜索范围为[0,0.5]。遗传算法其它参数设置同上节数值试验。

5.3 涡激力气动参数识别

以图4无量纲位移响应为拟合目标，重复50次拟合，发现拟合结果大都收敛于μ1=0.394，μ3=3.242。图6为拟合结果与原始样本时程对比，可发现二者幅值、相位均吻合较好。识别出μ1，μ3后，由样本无量纲幅值均值At=4.50×10-3，通过式(17)迭代最终得μ2的值：

μ2=77732.02

(18)

据μ1,μ2,μ3定义最终确定该主梁断面涡激力气动参数，见表1。

表1 流线型箱梁断面涡激力气动参数识别结果

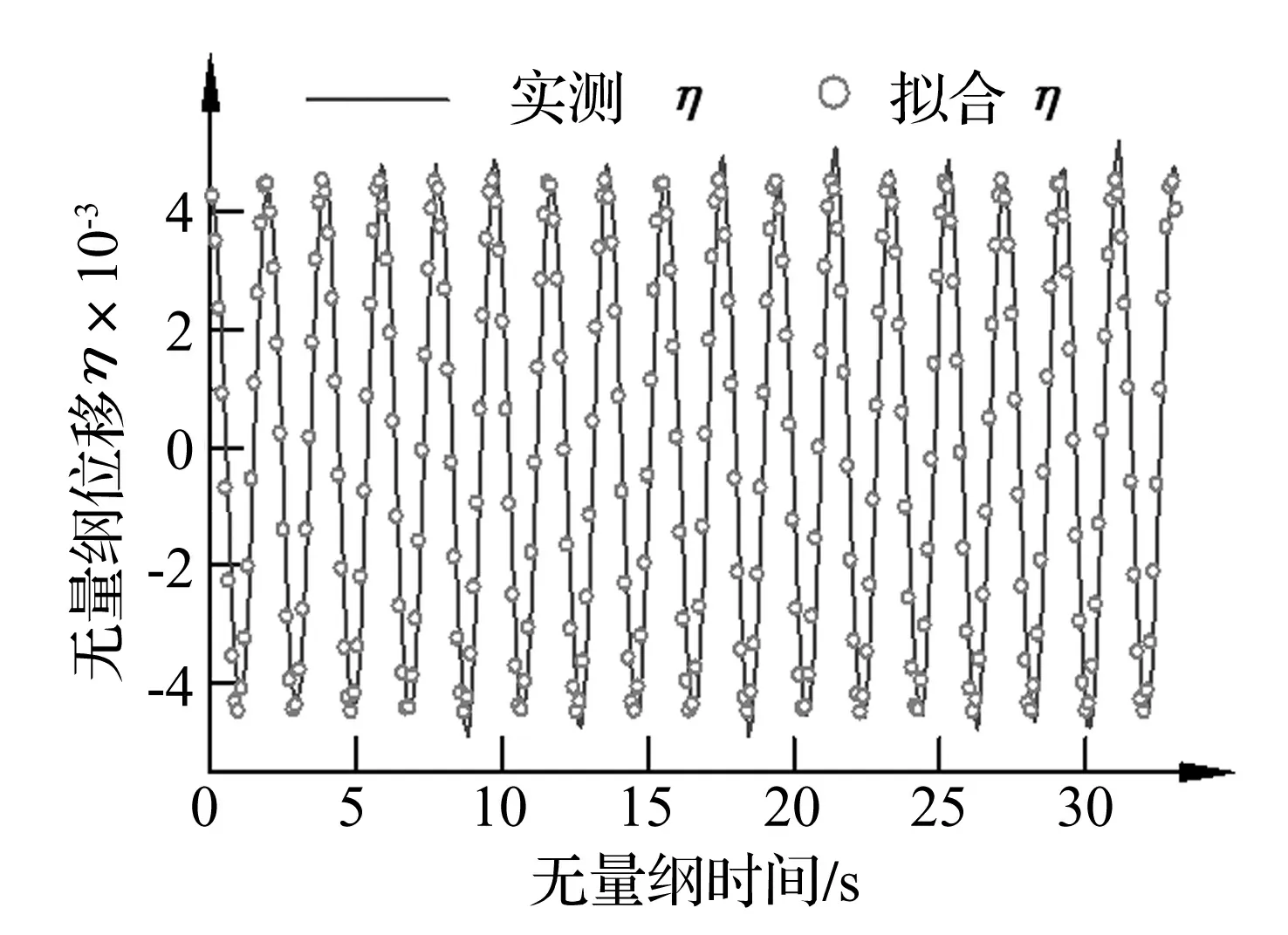
图6 拟合结果与原始位移时程对比

5.4 识别结果评价

分析识别所得非线性涡激力模型三个气动参数发现，识别的Y1(K)与相似桥梁断面在基本一致的折算频率下采用基于缓变参数的广义谐波函数KBM法[4]识别结果较接近。与气动刚度相关的Y2(K)为负值且绝对值相对较小，表明在该节段模型涡振锁定区，气动刚度作用使模型振动卓越频率略高于固有频率。通过该锁定风速下模型竖弯涡振响应频谱图发现，系统振动的卓越频率由零风速f=5.664 Hz提高至f=5.694 Hz。该微量的提高已表明Y2(K)识别结果的合理性。与文献[1,3]相比，本文识别的非线性阻尼项气动参数ε较大。分析非线性涡激力模型式(1)，其模拟涡振限幅自激特性机理通过非线性气动阻尼随质点振动过程变化进而导致系统总阻尼发生正负交替变化，表明非线性阻尼项中εx2/D2必为与1有相同量级的数。基于此，本文采用无量纲位移量级10-3较文献[1,3]的10-2小。考虑折算频率K及试验中采用的桥梁断面差别，本文对参数ε的识别结果具有合理性。

6 结 论

(1)通过对单自由度经验非线性涡激力模型进行变换，将其转化为标准Van der Pol振子形式。在求析解时，考虑非线性振动传统求解方法对运动平衡方程中小参数的依赖性，选择与系统参数值大小无关的同伦分析法获得Van der Pol振子的近似解。

(2)拟合过程引入能在待拟合参数定义域范围内进行全局最优搜索的遗传算法进行参数识别。光滑及有噪位移时程数值试验结果表明本文所提方法具有可行性及稳定性。

(3)利用该方法拟合风洞试验实测试数据时，针对遗传算法拟合所需参数范围因在气动参数未知情况下较难确定问题，通过比较相平面内极限环方法予以解决。用该方法对流线型闭口箱梁节段模型的涡激气动参数进行识别。拟合结果表明，该方法能有效用于风洞试验且识别结果稳定性较高。

参 考 文 献

[1]Ehsan F,Scanlan R H,ASCE M, Vortex-induced vibrations of flexible bridges[J]. Journal of Engineering Mechanics, 1990, 116(6):1392-1411.

[2]Gupta H, Sarkar P P, Mehta K C.Identification of vortex- induced-response parameters in time domain[J]. Journal of Engineering Mechanics-Asce, 1996. 122(11):1031-1037.

[3]Marra A M, Mannini C,Bartoli G.Van der Pol-type equation for modeling vortex-induced oscillations of bridge decks[J].Journal of Wind Engineering and Industrial Aerodynamics, 2011,99(6-7):776-785.

[4]周 涛, 朱乐东, 郭震山.经验非线性涡激力模型参数识别[J]. 振动与冲击, 2011,30(3):115-118,144.

ZHOU Tao, ZHU Le-dong, GUO Zhen-shan.Parameters identification on nonlinear empirical model for vortex-induced vibration(VIV)[J]. Journal of Vibration and Shock, 2011, 30(3): 115-118,144.

[5]Scanlan R H.State-of-the-art methods for calculating flutter, vortex-induced, and buffeting response of bridge structures [M].Nat.Tech. Information Service,1981.

[6]LIAO Shi-jun.An analytic approximate approach for free oscillations of self-excited systems[J]. International Journal of Non-Linear Mechanics, 2004,39(2):271-280.

[7]Holland J H.Genetic algorithms[J]. Scientific American, 1992, 267(1):66-72.

[8]López J L,López-Ruiz R.Approximating the amplitude andform of limit cycles in the weakly nonlinear regime of Liénardsystems[J]. Chaos, Solitons & Fractals, 2007,34(4):1307-1317.