基于双树复小波和奇异差分谱的齿轮故障诊断研究
胥永刚, 孟志鹏, 陆 明, 付 胜
(北京工业大学 机电学院 先进制造技术北京市重点实验室, 北京 100124)
齿轮是机械设备中应用十分广泛的零部件之一,恶劣的工作环境使其非常容易出现故障。而齿轮故障直接影响设备运行的可靠性以及产品质量和生产效率,因此对齿轮故障诊断进行研究具有十分重要的意义。由于其破坏形式极其复杂, 且通过传感器提取出来的齿轮振动加速度信号具有非平稳特征,反映状态信息的能量也很微弱,给故障诊断带来了困难。如何从非平稳的振动信号中提取出故障特征信息是齿轮故障诊断的关键[1]。
近年来,国内外的学者对齿轮的诊断研究做了大量的工作,主要集中在典型故障特征的提取研究上,并取得很多的成绩。对于实际对象的齿轮故障诊断,如用单一的方法,有时难以准确快速地完成对复杂对象的故障诊断。因此,往往将多种信号处理方法结合来提取故障特征信息,李辉等[2]将EMD和功率谱结合;程军圣等[3]将LMD与谱峭度结合;袁海英等[4]将提升小波变换和Hilbert解调结合;孙伟等[5]将小波包与LMD 结合等用于齿轮故障诊断中都取得了较好的效果。
为构建具有平移不变性的小波,有效消除信号分析中的频率混叠,Kingsbury[6]首先提出双树复小波变换的概念,Selesnick等[7]进一步提出了双树复小波变换的分解与重构算法。双树复小波变换不仅保持了传统小波变换的时频局部化分析能力,还具有近似平移不变性、良好的方向选择性、完全重构性、有限的数据冗余性和高效的计算效率等优良性质。目前双树复小波变换已经广泛的应用于图像处理[8]、信号降噪[9]和故障诊断等领域[10]。
奇异值分解具有理想的去相关特性[11], 基于奇异值分解的信号分析方法可以对信号进行重构, 较好的从背景噪声中分离出有用信号的特征信息。在故障诊断领域中,奇异值分解技术主要用于降噪和提取信号中的周期成分[12-15]。奇异值差分谱用来描述信号中有用成分和噪声的奇异值的本质差异,根据差分谱的最大突变位置可以准确地确定有效奇异值的个数。
本文提出了基于双树复小波和奇异差分谱的故障诊断方法,并将其成功应用于机械故障诊断中。实验和工程案例均表明,该方法可以有效的提取齿轮的故障特征频率。
1 双树复小波变换
双树复小波变换(Dual-Tree Complex Wavelet Transform, DT-CWT)是基于实数小波变换实现的复数小波变换, 它通过两个并行的实数滤波器组来实现, 分别称为实部树和虚部树,DT-CWT的三层分解与重构过程如图1所示[6-7]。其中低通滤波器h0和高通滤波器h1构成实部树的分析滤波器组,低通滤波器g0和高通滤波器g1构成虚部树的分析滤波器组。为了实现实部树和虚部树的信息互补,在信号的分解与重构过程中,始终保持虚部树的采样位置位于实部树的中间,使双树复小波变换能有效综合利用实部树和虚部树的小波分解系数。这种小波分解算法使双树复小波变换具有近似平移不变性,并减少了有用信息的丢失。双树复小波变换在各层的分解过程中,利用小波系数二分法减少了多余的计算,从而提高了计算速度。从双树复小波变换的分解和重构图中,可以看出实部树和虚部树之间没有数据流动,因此双树复小波算法的计算时间只是传统小波变换的两倍。
根据双树复小波的构造方法,复小波可表示为:
φ(t)=φh(t)+iφg(t)
(1)
式中:φh(t),φg(t)表示两个实小波;i为复数单位。
由于双树复小波变换由两个并行的小波变换组成,因此,根据小波理论,上面实部树小波变换的小波系数和尺度系数可由式(2)和式(3)计算:
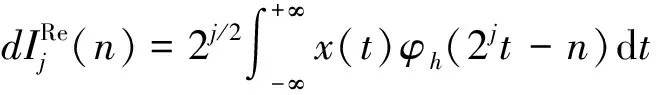
(2)
(3)
同理,下面虚部树小波变换的小波系数和尺度系数可由式(4)和式(5)计算:

(4)
(5)
因此,双树复小波变换的小波系数和尺度系数:
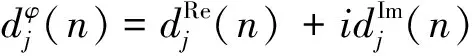
(6)
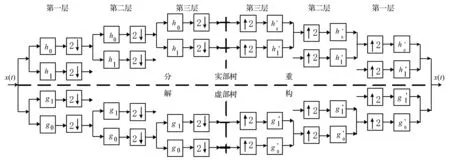
图1 双树复小波变换的分解和重构过程
(7)
最后,双树复小波变换的小波系数和尺度系数可由式(8)和式(9)进行重构:

(8)
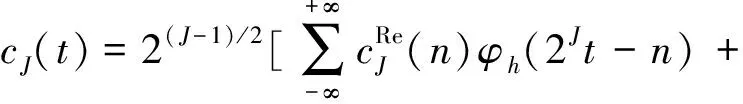
(9)
双树复小波变换后的重构信号可表示为:
x(t)=dj(t)+cJ(t)
(10)
2 奇异值差分谱
设有Y=(y(1),y(2),…,y(N))为离散数字信号,应用奇异值分解时,首先需将信号构造为矩阵H,H多为Hankel矩阵,具体构造方式如下:
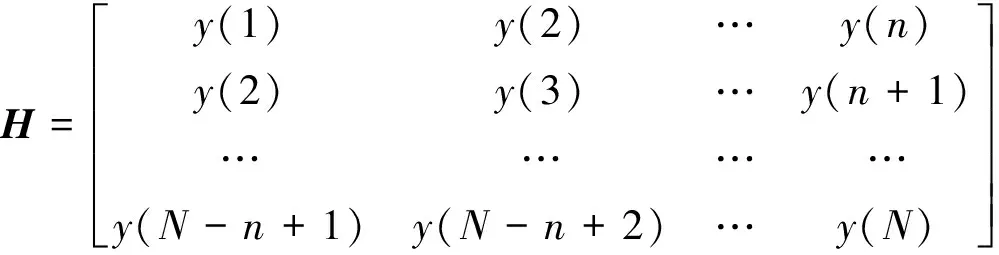
(12)
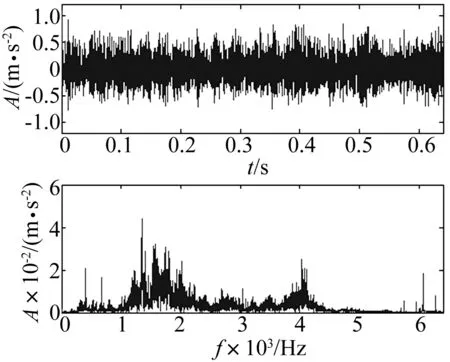
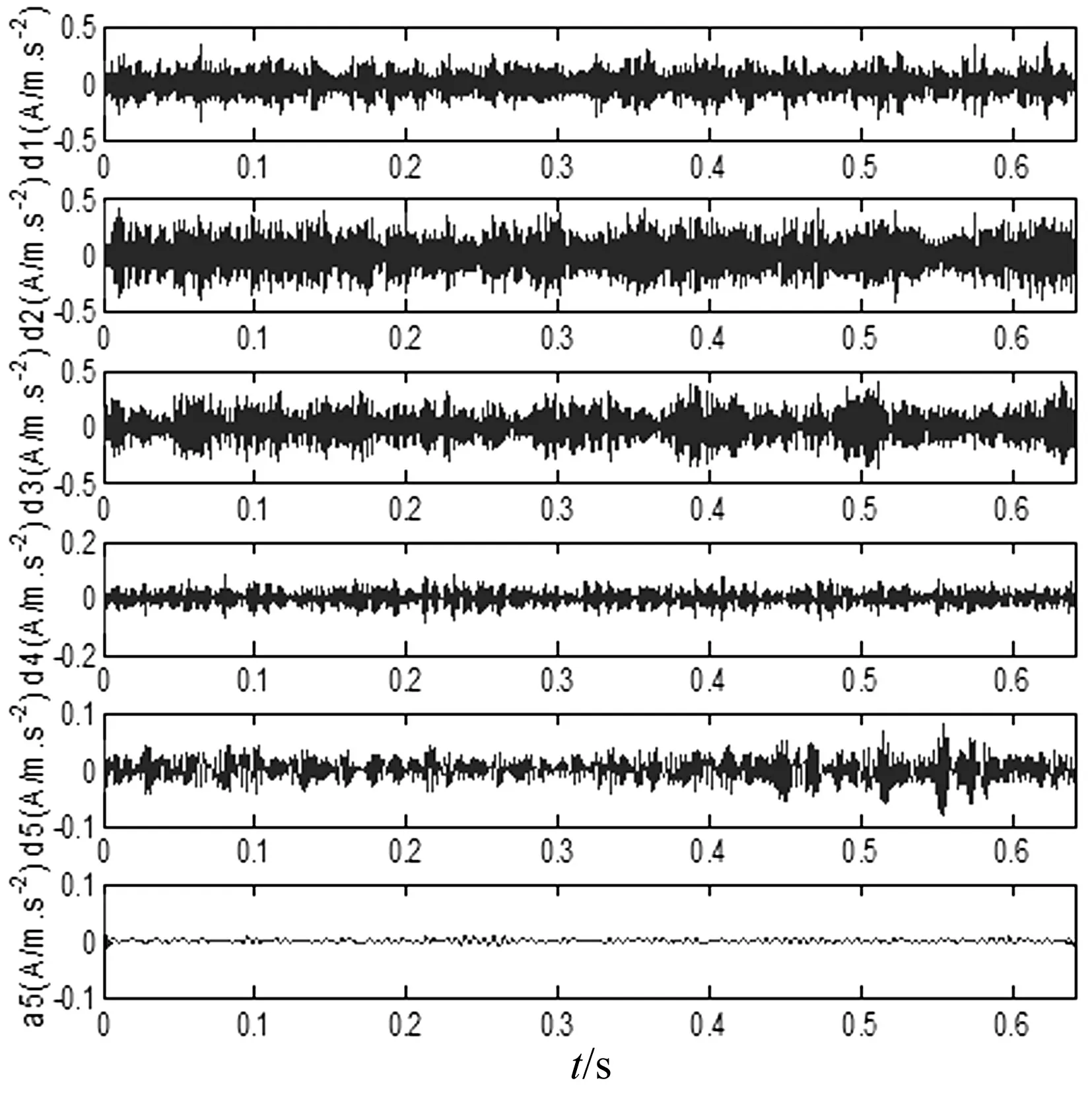
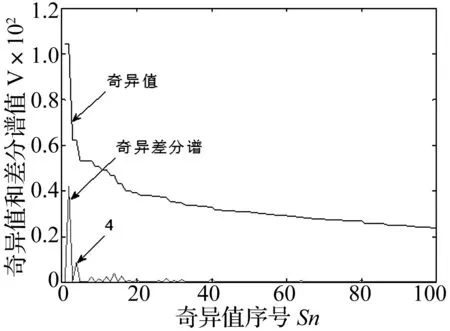
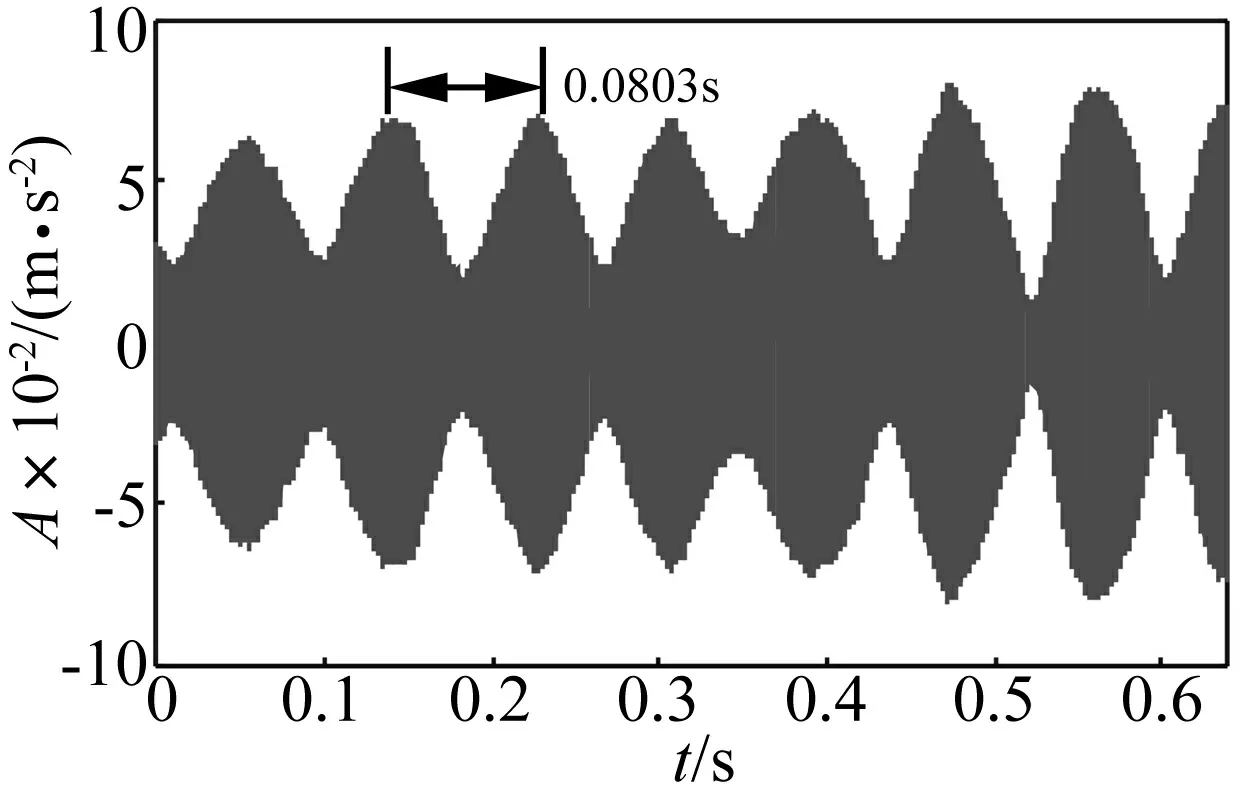
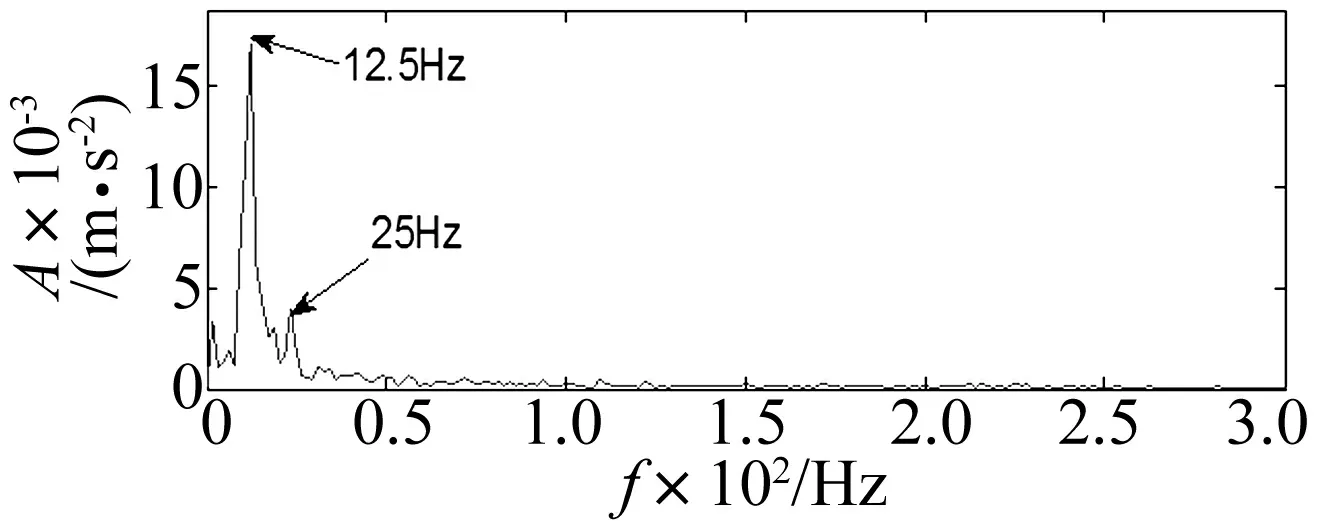
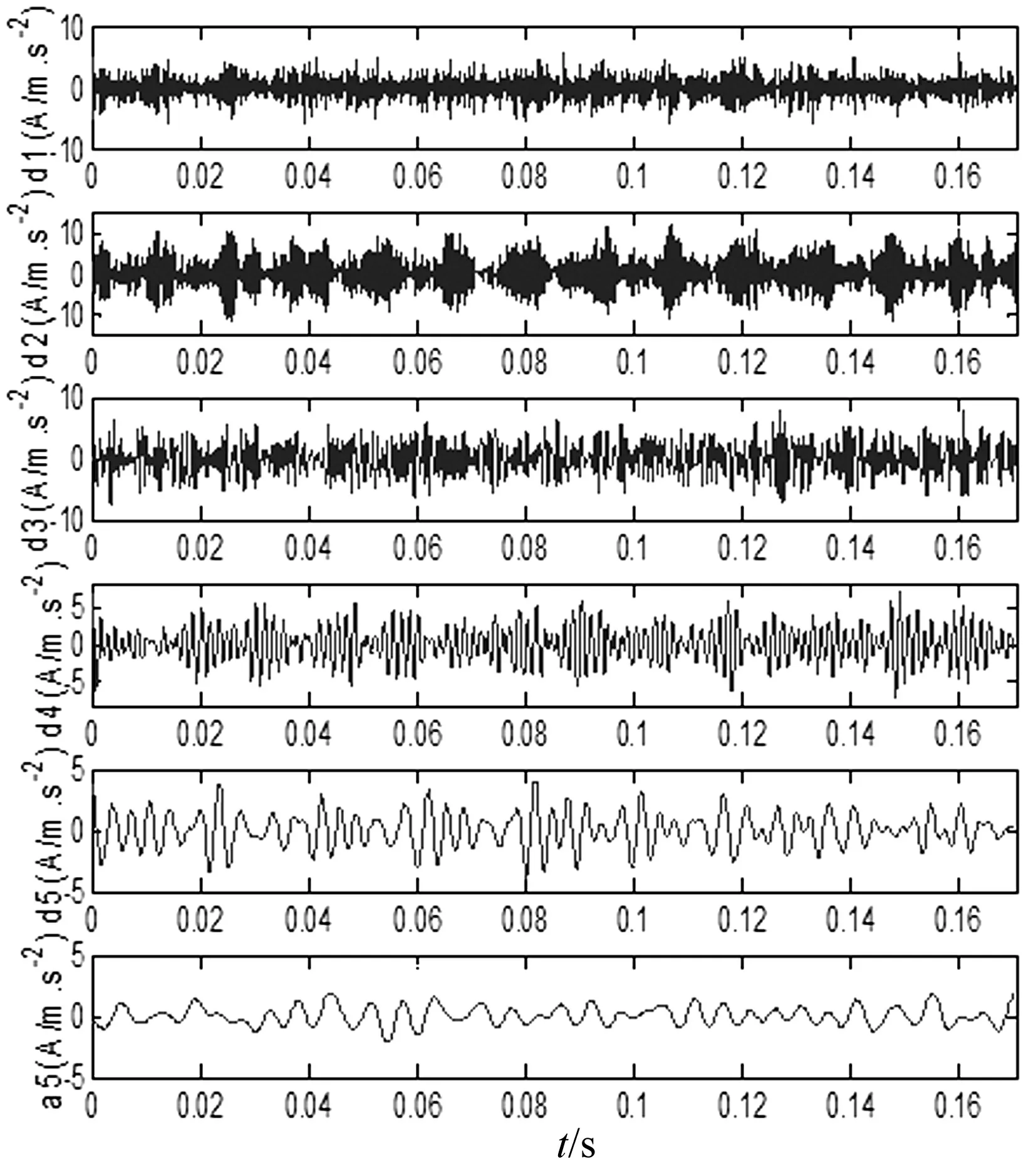
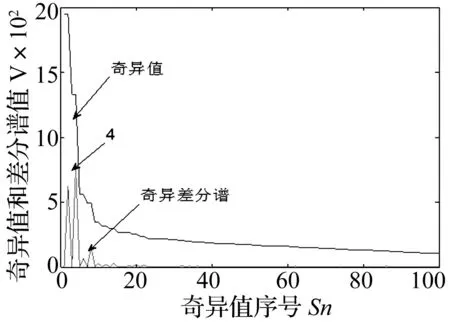
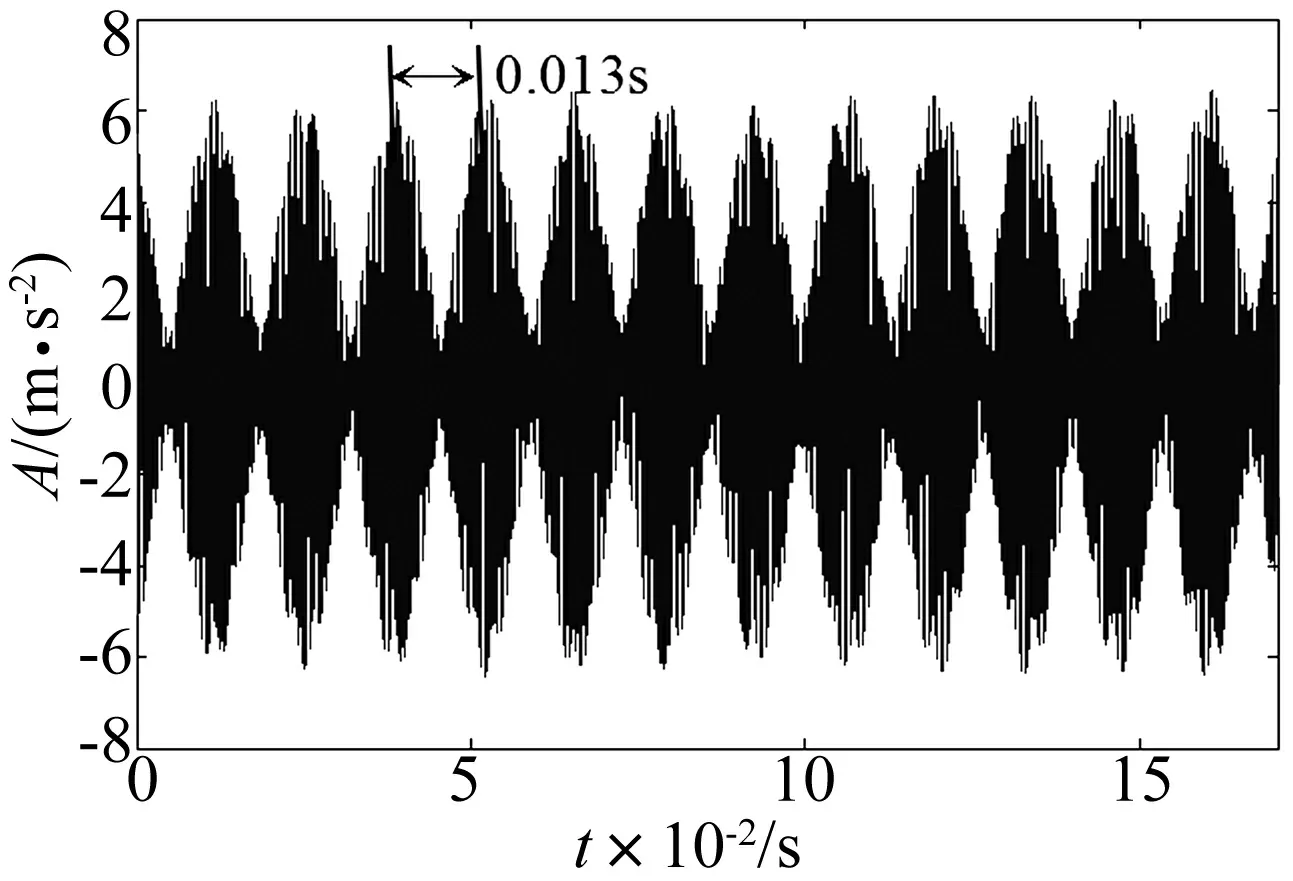
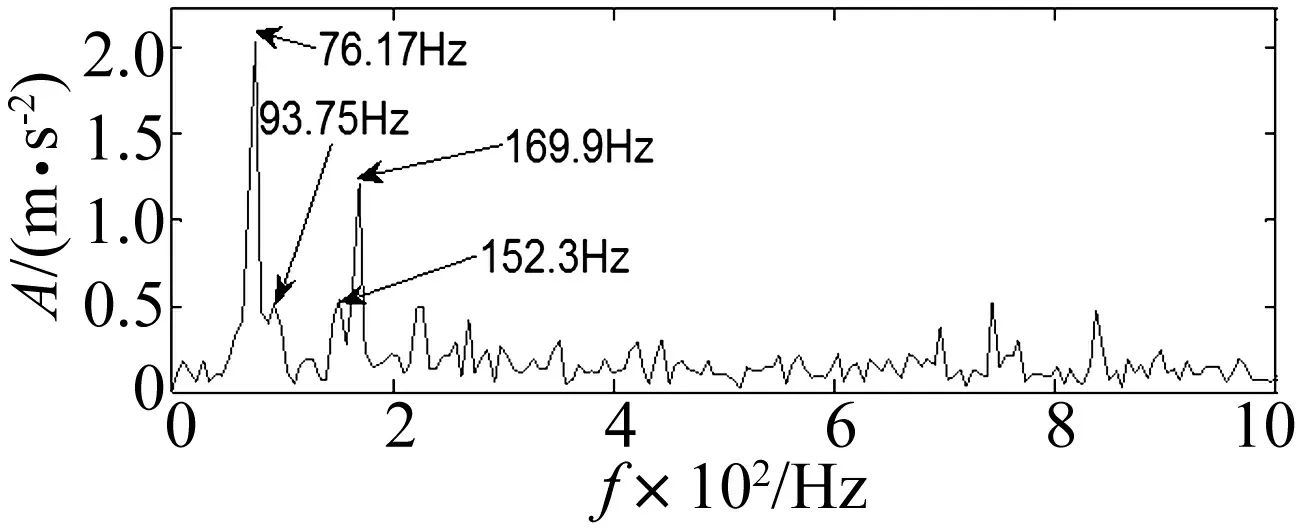
式中,1 奇异值分解(Singular Value Decomposition, SVD)的定义:一个实矩阵H∈Rm×n, 不管其行列是否相关,必定存在一对正交矩阵U=(u1,u2,…,um)∈Rm×m和V=(v1,v2,…,vn)∈Rn×n,使得: H=USVT (13) Hankel矩阵的特点是:矩阵的后一行总是比前一行滞后一个数据点,对于理想信号所构造的Hankel矩阵是一种病态矩阵,相邻的行都是高度相关的。这种病态矩阵的前几个奇异值比较大,后面的奇异值非常小,都近似于零,奇异值在某一点(即矩阵的秩所对应的点)处发生突变。而对含噪声的信号,尽管前后两行也滞后一个数据点,但却互不相关,是一个良态满秩的矩阵。 对于含噪信号构造的Hankel 矩阵有后面的q-k个奇异值明显小于前k个奇异值,也就是说奇异值在第k个点发生突变,而前k个奇异值代表了要提取的理想信号。由于每一个奇异值对应着一个分量信号,因此,只要选择前面k个分量进行简单的叠加,就可获得降低了噪声的信号。 SVD降噪的关键问题就是需要合理地选择出前面的若干个奇异值进行SVD逆运算,如果奇异值数目选择过多,则会使处理结果混进一部分噪声,而选择过少却又会丢掉信号中的有用成分,有时甚至会造成信号波形的畸变。 为了实现对有效奇异值个数的自动判断,定义奇异值差分谱。设所有奇异值按照从大到小的顺序形成的序列为S=σ1,σ2,…σq,则: bi=σi-σi+1i=1,2,…,q-1 (14) 将所有bi组成的序列B=(b1,b2,…,bq-1)称为奇异值的差分谱,它描述了两两相邻奇异值的变化情况,当两相邻奇异值差别较大时,在差分谱中必将产生一个峰值,而在整个差分谱中必然存在一个最大峰值bk,根据差分谱的定义,这意味着奇异值序列在位置k处发生了最大突变。 奇异值在最大突变点处产生的最大差异根本原因就在于有用信号和噪声的相关性不同而在奇异值上表现出来的自然反应。 基于DT-CWT和奇异差分谱诊断的方法首先将信号进行DT-CWT分解, 得到几个不同频段的分量。然后选择某个含有故障特征信息的分量,对其SVD分解,求差分谱选择奇异值个数, 进行SVD重构,从而实现信号的降噪,并求其希尔伯特包络谱,找到故障频率,进行更为准确的故障识别[15-18]。该方法实现流程如图2所示。 图2 基于DT-CWT和奇异差分谱的诊断方法 Fig.2 The method based on DT-CWT and different spectrum of singular value 其诊断具体步骤如下: (1)通过对原始振动信号进行双树复小波分解, 得到几个频段不同的分量。 (2)对包含故障特征的分量, 构建Hankel矩阵。 (3)对Hankel矩阵进行奇异值分解。 (4)求奇异差分谱, 并画出差分谱曲线图。确定谱图中最大突变点, 即需要保留奇异值的个数,其余的奇异值置为零。 (5)根据步骤(4)中确定的奇异值个数,进行奇异值重构, 从而消除噪声,并求希尔伯特包络谱。 (6)从希尔伯特包络谱中确定故障特征信息。 实验台如图3所示,实验系统由齿轮故障模拟实验台、压电式加速度传感器、数据采集仪、笔记本电脑组成。将有故障的齿轮安装在齿轮箱内,进行实验数据的采集,数据采集仪将采集数据传到电脑中,再进行数据处理分析。 该实验中齿轮箱是一对齿轮,模数为2,材质是S45C,小齿轮为主动轮,齿数Z1为55;大齿轮为从动轮,齿数Z2为75。该故障实验模拟了大齿轮一个齿齿根微小裂纹故障,电机转速N为1 000 r/min,采样频率为12 800 Hz。 根据以上参数,按照以下公式: (15) 可得大齿轮的故障特征频率为fZ2为12.22 Hz。 图3 故障实验台 图4为齿轮裂纹故障的原始时域波形及幅值谱,从波形和幅值谱中基本看不出故障特征信息,同时有明显的干扰成分。故利用DT-CWT对原始信号进行5层分解,然后进行单支重构,各层重构信号为a5、d5、d4、d3、d2和d1,得到如图5所示的不同频段的分量,可以看出第三个分量d3出现了微弱的周期性冲击成分。 图4 齿轮裂纹故障波形及频谱 图5 双树复小波分解图 将第三个分量d3作为研究对象,构造Hankel矩阵,进行奇异值分解并求得奇异值序列,进而求得奇异值差分谱,奇异值差分谱峰突变在前段部分,后面的都趋于零。为了清楚的观察差分谱的情况,将奇异值序列和差分谱前100个点绘在一个坐标系下, 如图6所示。从图中可以看到最大突变在第2个点,如果最大突变点发生在前两个点,往往取第2个最大突变点,因为奇异值分量太少会丢失有效信息。第二最大突变点为第4点,故保留SVD分解的前4个奇异值,其余的奇异值为0,进行奇异值重构得到如图7所示结果。信号呈现非常好的周期性冲击,冲击周期大约为0.080 3 s,对应的频率为12.45 Hz,与大齿轮故障特征频率非常接近。 图6 奇异值和差分谱前100个点 图7 重构SVD 前4个奇异值的信号波形 图8 SVD重构后信号的希尔伯特包络谱 对图7所示的重构信号进行希尔伯特包络解调,得到如图8所示的包络谱,可以很清楚的看到12.5 Hz和25 Hz的频率,与大齿轮故障特征频率的一倍和二倍频非常接近,可以断定该大齿轮已经发生故障。 图9所示为直接对双树复小波分解和重构后得到的第3个分量d3作希尔伯特包络谱,虽然也可以看到12.5 Hz和25 Hz的频率,但同时还存在一系列明显的干扰频率成分,如9.3 Hz、17.19 Hz、20.31 Hz等,易造成误诊断。上述结果表明,双树复小波和奇异值差分谱结合,可以有效的提取齿轮故障的特征频率。 图9 d3分量的希尔伯特包络谱 某钢铁公司一高线第25架精轧机于2007年8月1日出现齿轮箱Z5/Z6齿轮打齿故障,如图10所示,其中故障特征频率为76.172 Hz。图11为早期故障数据(6月30日)波形图和频谱图。从波形中基本看不出故障特征信息,在频谱中可以看到一些边频的出现,但是特征不是很明显,无法准确识别故障齿轮对应的特征频率。 为了提取故障特征,本文首先利用双树复小波对原始信号进行5层分解并重构,得到如图12所示结果,可以看出第二个分量d2有较为明显的冲击成分。故对d2求奇异值差分谱如图13所示。 图10 齿轮箱损坏图 图11 6月30日故障齿轮波形及频谱 图12 双树复小波分解图 图13 奇异值和差分谱前100个点 根据图13所示,在第2点和第4点都出现了较大突变,如果最大突变点发生在前两个点,往往取第2个最大突变点,因为奇异值分量太少会丢失有效信息;对于同时存在多个较大突变点,只需选择最大突变点即可。图13中最大突变点在第4个点,将奇异值分解的前4个奇异值重构,结果如图14所示,信号呈现非常好的周期性冲击,冲击周期大约为0.013 s,对应的频率为76.9 Hz,与齿轮故障特征频率非常接近。再对图14所示的重构信号进行希尔伯特包络解调得到如图15所示的包络谱,可以很清楚的看到76.21 Hz,146.6 Hz和222.8倍频,与齿轮故障特征频率76.172 Hz的一倍、二倍和三倍频非常接近。 图14 重构前4个奇异值的信号波形 图15 SVD重构后的希尔伯特包络谱 图16 d2的希尔伯特包络谱 图16所示为直接对双树复小波分解和重构后得到的第2个分量d2的希尔伯特包络谱,也可找到76.21 Hz和152.3 Hz的频率,但存在93.75 Hz和169.9 Hz的频率干扰成分,不利于对故障部位做出准确判断。 本文研究了将双树复小波分解与奇异值差分谱结合的方法,通过齿轮故障实验和工程案例验证了方法的有效性。 (1)利用双树复小波变换具有近似平移不变性、避免频率混叠和有效降噪的优点,对齿轮故障振动信号进行双树复小波分解和重构,得到不同频段的分量。 (2)根据奇异值差分谱理论,可以自动的判定SVD分解奇异值重构的个数,保留了信号中有用成分,同时又最大限度地消除了噪声。 (3)将双树复小波分解与奇异值差分谱结合的方法应用于故障诊断中,可以有效和准确的找到故障特征信息。 参 考 文 献 [1]Peng Z, Chu F, He Y. Vibration signal analysis and feature extraction based on reassigned wavelet scalogram [J]. Journal of Sound and Vibration, 2002, 253(5):1087-1100. [2]李 辉,郑海起,唐力伟. 基于EMD和功率谱的齿轮故障诊断研究[J]. 振动与冲击,2006,25(1):133-135,145. LI Hui, ZHENG Hai-qi, TANG Li-wei. Study on fault diagnosis of gear crack based on EMD and power spectrum analysis [J]. Journal of Vibration and Shock, 2006,25(1):133-135,145. [3]程军圣,杨 怡,杨 宇. 基于LMD 的谱峭度方法在齿轮故障诊断中的应用[J]. 振动与冲击,2012,31(18):20-23. CHENG Jun-sheng, YANG Yi, YANG Yu. Application of spectral kurtosis approach based on local mean decomposition (LMD)in gear fault diagnosis [J]. Journal of Vibration and Shock, 2012,31(18):20-23. [4]袁海英,黎海涛,梅家平.基于提升小波变换和Hilbert调制技术的故障识别方法[J].北京工业大学学报,2012,38(12):1835-1838. YUAN Hai-ying, LI Hai-tao, MEI Jia-ping. Fault recognition method based on lifting wavelet transform and hilbert modulation technology[J].Journal of Beijing University of Technology, 2012,38(12):1835-1838. [5]孙 伟,熊邦书,黄建萍,等.小波包降噪与LMD 相结合的滚动轴承故障诊断方法[J].振动与冲击,2012,31(18):153-156. SUN Wei, XIONG Bang-shu, HUANG Jian-ping, et al. Fault diagnosis of a rolling bearing using wavelet packet de-noising and LMD[J].Journal of Vibration and Shock, 2012,31(18):153-156. [6]Kingsbury N G. The dual-tree complex wavelet transform:a new technique for shift invariance and directional filters[J]. IEEE Digital Signal Processing Workshop,1998,98(1):2-5. [7]Selesnick I W, Baraniuk R G, Kingsbury N G. The dual-tree complex wavelet transform[J]. IEEE Digital Signal Processing Magazine, 2005, 22(6):123-151. [8]Celik T, Ozkaramanl H, Demirel H. Facial feature extraction using complex dual-tree wavelet transform [J].Computer Vision and Image Understanding, 2008, 111(2):229-246. [9]苏文胜,王奉涛,朱 泓,等.双树复小波域隐Markov树模型降噪及在机械故障诊断中的应用[J].振动与冲击,2011,30(6):47-52. SU Wen-sheng, WANG Feng-tao,ZHU Hong, et al. Denoising method based on hidden Markov tree model in dual tree complex wavelet domain and its application in mechanical fault diagnosis [J]. Journal of Vibration and Shock, 2011,30(6):47-52. [10]艾树峰.基于双树复小波变换的轴承故障诊断研究[J].中国机械工程,2011,22(20):2446-2451. AI Shu-feng .Research on bearing fault diagnosis based on daul-tree complex wavelet transform[J]. China Mechanical Engineering, 2011,22(20):2446-2451. [11]Kakarala R, Ogunbona P O. Signal analysis using a multiresolution form of the singular value decomposition [J]. IEEE Transactions on Image Processing,2001,10(5):724-735. [12]刘献栋,杨绍普,申永军,等.基于奇异值分解的突变信息检测新方法及其应用[J].机械工程学报,2002,38(6):102-105. LIU Xian-dong,YANG Shao-pu,SHEN Yong-jun,et al. New method of detecting abrupt information based on singularity value decomposition and its application[J]. Journal of Mechanical Engineering, 2002,38(6):102-105. [13]Yang W X, Peter W T. Development of an advanced noise reduction method for vibration analysis based on singular value decomposition [J]. NDT&E International, 2003, 36(6):419-432. [14]李 建,刘红星,屈梁生.探测信号中周期性冲击分量的奇异值分解技术[J].振动工程学报,2002,15(4):415-418. LI Jian,LIU Hong-xing, QU Liang-sheng, Detection of periodic impulse components in signals using singular value decomposition[J].Journal of Vibration Engineering, 2002, 15(4):415-418. [15]吕志民,张武军,徐金梧,等.基于奇异谱的降噪方法及其在故障诊断技术中的应用[J].机械工程学报,1999,35(3):85-88. LÜ Zhi-min, ZHANG Wu-jun, XU Jin-wu,et al. A noise reduction method based singular spectrum and its application in machine fault diagnosis [J].Chinese Journal of Mechanical Engineering, 1999, 35(3):85-88. [16]赵学智,叶邦彦,陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J].机械工程学报,2010,46(1):100-108. ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe [J]. Journal of Mechanical Engineering, 2010, 46(1):100-108. [17]张 超,陈建军,徐亚兰.基于EMD分解和奇异值差分谱理论的轴承故障诊断方法[J].振动工程学报,2011,24(5):539-545. ZHANG Chao, CHEN Jian-jun, XU Ya-lan. A bearing fault diagnosis method based on EMD and difference spectrum theory of singular value [J]. Journal of Vibration Engineering, 2011,24(5):539-545. [18]赵学智,叶邦彦,陈统坚.基于小波-奇异值分解差分谱的弱故障特征提取方法[J].机械工程学报,2012,48(7):37-47. ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian. Extraction method of faint fault feature based on wavelet-SVD difference spectrum [J]. Journal of Mechanical Engineering, 2012,48(7):37-47.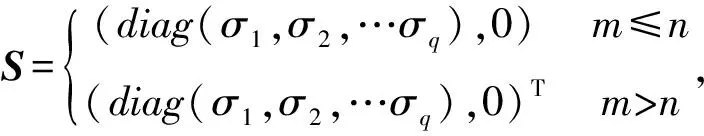
3 DT-CWT和奇异差分谱诊断方法

4 实验分析


5 工程案例



6 结 论

