基于Solidworks和ANSYS的加工中心电主轴动静态分析

尹 洋1，王 宇1，秦军军1，孙惠娟2，董翠云

(1.西华大学机械工程与自动化学院，四川 成都 610039；2.四川大学制造科学与工程学院，四川 成都 610025；3.青岛科技大学机电工程学院，山东 青岛266042)

电主轴是实现机床高速化的主要部件，高速加工中心对电主轴的技术指标有着非常严格的要求；因此，电主轴的可靠性、安全性、加工精度和使用寿命等是机床结构设计和机床运行应主要考虑的问题[1]。本文研究的某型号加工中心电主轴系统主要通过经验设计完成， 缺乏详细的理论分析和验证。基于此，笔者利用Solidworks和ANSYS软件对此电主轴系统进行静态分析、模态分析和谐响应分析，通过分析得出电主轴的静刚度、临界转速、前四阶振型及固有频率，为评价该电主轴的动静态特性以及后面的设计改造提供了实验数据，为这种类型的电主轴设计改进提供了参考。

1 模型的建立

ANSYS中有限元模型的生成有2种方法：利用ANSYS直接进行实体建模，然后网格化得到有限元模型；利用Solidworks、Pro/E等绘图软件建立实体模型，再导入到ANSYS中转化成有限元模型。 ANSYS的建模功能相对来说不如专业绘图软件强大且操作较为不便， 因此，本文采用在Solidworks中建模，然后导入ANSYS的方法。一般通用的做法是转为IGES格式，然后导入，但这种方法不太理想，容易出现破面、多线等问题[2-3]；因此本文采用另外一种方法。具体操作如下。

根据电主轴的设计数据，在Solidworks中建立其三维模型，如图1所示，然后将该模型另存为Parasolid(*.x_t)格式， 在ANSYS的菜单栏file下选择import—PARA……，将已保存的Parasolid(*.x_t)格式文件导入，在菜单栏依次选择PoltCtrls—Style—Solid Model Facets，再选择Normal Faceting下拉选项，最后在菜单栏选择PoltVolumes即可生成实体模型。

图1 主轴三维模型图

该电主轴是一种中空、多支承的阶梯轴，有前后2组轴承作为支撑，主轴前端承受集中切削力、弯矩、转矩，后轴承主要承受内装电机转子传递给主轴的转矩等。图2为主轴的受力情况分布图。

图2 主轴受力分析图

针对轴承受多种载荷作用且具有非线性弹性形变的特点，在建立电主轴有限元模型时，作如下简化: 将角接触球轴承简化为只有径向刚度，没有角刚度的弹性支承，利用弹簧阻尼单元Combin14来模拟轴承结构；忽略轴承负荷对轴承刚度的影响，利用Solid45 单元来模拟整根轴。最后得到的有限元模型如图3所示，主轴的最高转速为8 000 r/min，材料为40Cr,材料的弹性模量为220 GPa，泊松比为0.3。

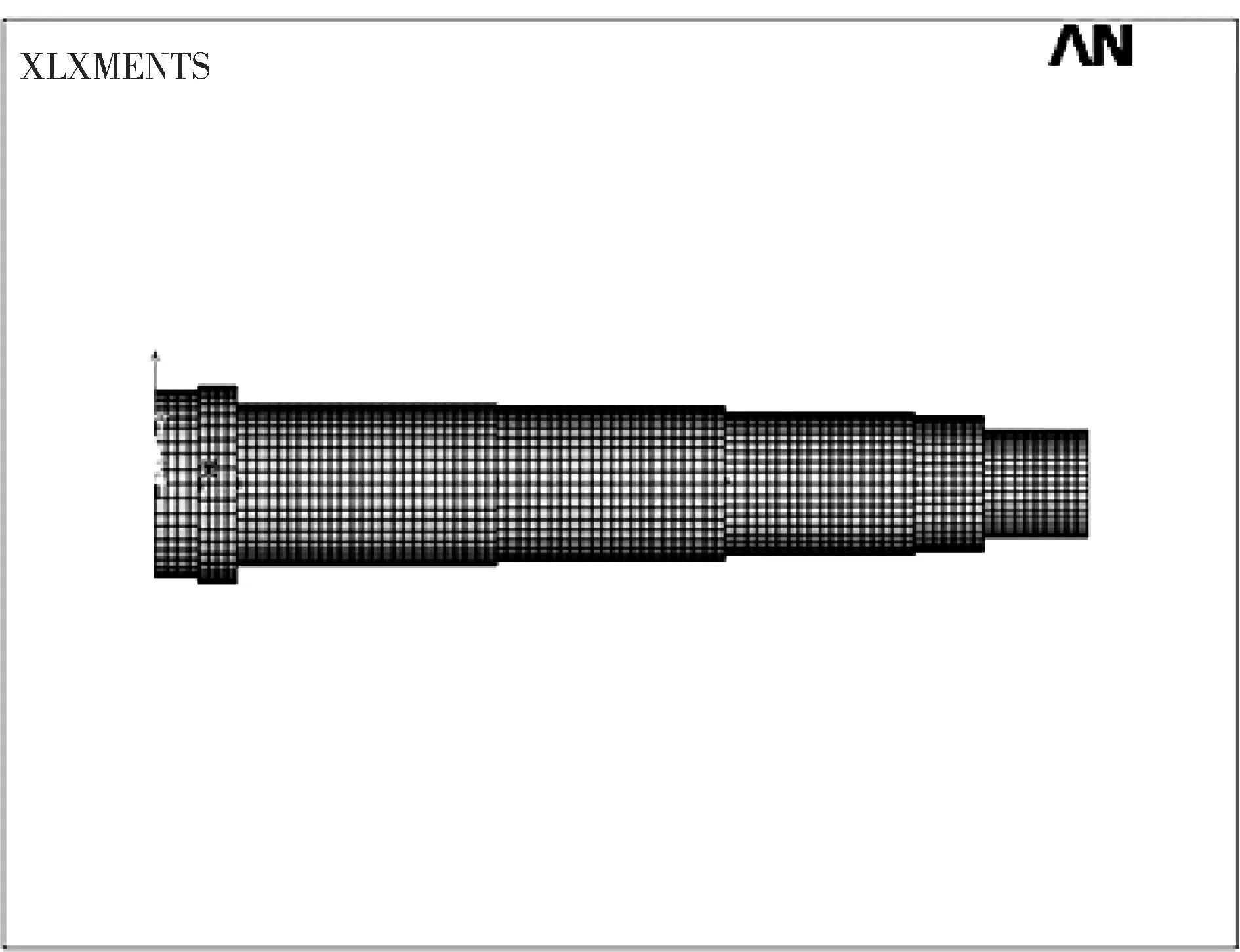
图3 主轴有限元模型

2 电主轴的静态特性分析

主轴的静刚度简称主轴刚度，是机床主轴系统重要的性能指标，与负荷能力及抗振性能密切相关[4]。

主轴刚度分为轴向刚度和弯曲刚度。一般情况下，主轴主要承受径向切削力，而轴向受力很小，所以其弯曲刚度远比轴向刚度重要。主轴单元的弯曲刚度K是指在主轴前端产生单位径向位移δ时所需施加的径向力，即

K=Fr/δ(N/μm)

(1)

对图3所示的有限元模型,进行线性静力分析，进入 ANSYS 中的Solution模块，并设置弹簧—阻尼单元，根据轴承安装的实际情况，轴前端约束为轴向和径向，后端仅约束径向，在主轴前端点施加径向载荷2.95 kN。经过分析得到主轴的静力变形如图4所示，节点应力等值线如图5所示，从而得到主轴前端的最大径向变形为11.9 μm，电主轴的静刚度K=Fr/δ=247.90 N/μm,而主轴的静刚度要求为216 N/μm；因此，该电主轴的静刚度满足要求。

图4 静力变形图

图5 主轴节点应力等值线图

3 电主轴的模态分析

模态分析经常用于研究机构或机器部件的振动特性，是后续动力学分析问题的基础，如谐响应分析、瞬态动力学分析和谱分析[5]。

模态分析常用的方法有子空间法(subspace)和分块兰索斯法(block Lanczos)。分块兰索斯法与子空间法相比，求解精度高、求解效率高、计算速度较快，故本文采用分块兰索斯法。

结构的振动可以表示为各阶固有振型的线性组合，而固有振型的阶次越低，对结构的振动影响越大；因此，低阶振型对结构的动态特性起决定作用[6]。本文采用分块Lanczos法提取得到的主轴前四阶固有频率和振型，如表1所示，前四阶振型图如图6—9所示。

表1 主轴各阶固有频率和振型

图6 一阶振型图

图7 二阶振型图

图8 三阶振型图

图9 四阶振型图

由振型图可知：一阶振型表现为主轴前端径向一阶弯曲；二阶振型表现为主轴整体二阶弯曲变形；三阶振型表现为主轴轴向平动；四阶振型表现为甩尾。由表1知，模拟得到的一阶固有频率为962.72 Hz,计算得到主轴的一阶临界转速n=962.72×60=57 763.2 r/min。由此初步得出所设计的电主轴的工作转速远远低于其一阶临界转速，可以有效地避开共振区间，避免发生同频共振现象，从而能够保证机床的使用寿命和加工精度。

4 电主轴的谐响应分析

谐响应分析是一种用于分析结构承受已知频率的按正弦(简谐)规律变化的载荷作用时的稳态响应技术，用于分析连续的周期性载荷在系统结构中产生的周期性响应(谐响应)。电主轴在工作时，会有周期性的激振力(铣削力)作用在主轴上，产生连续的周期响应。当周期响应的激振力频率与主轴的固有频率相同时，就会发生同频共振。这种共振不仅会降低铣削加工精度，还会对刀具、工件甚至机床造成破坏；因此，在实际应用中必须避免此类事情发生[7-8]。进行谐响应分析在一定程度上可以预测发生共振的可能性。

本文使用的ANSYS软件提供了3种主要的谐响应分析方法：Full法、Reduced法、Mode Superposition法。此处采用Full法进行分析。

谐响应分析必须是在模态分析之后才能进行。在完成模态分析后，进入ANSYS的Harmonic分析模块，首先研究主轴在一阶固有频率962.72 Hz附近的响应特性，取激振力Fr幅值为120 N，激振频率为650～1 150 Hz，载荷子步为50，选用Full方法分析，得出主轴前端的径向振动曲线，如图10所示。

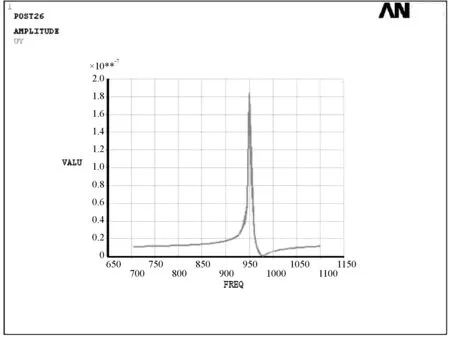
图10 主轴前端径向应位移—频率曲线图

可以看出：当激振力的频率在920 Hz以下时，主轴前端的振动幅度非常小，主轴运行非常平稳；当频率从920 Hz增大到950 Hz时，主轴端部的径向位移急剧增大，动刚度显著下降；当激振力频率超过950 Hz到达970 Hz附近时，端部位移又急剧减小，相应动态刚度显著下降并达到最低。由此可以推断：共振发生在频率为950 Hz附近，也就是一阶固有频率附近；当频率小于920 Hz或大于970 Hz时，主轴前端的动态位移量都很小，表明在此频率区间内，主轴具有良好的动刚度。本文所设计的电主轴最高转速为8 000 r/min,也就是最高工作频率为800 Hz；因此，可以有效地避开共振区，避免共振的发生，确保加工精度符合要求。

5 结束语

本文通过对轴承—主轴系统进行结构简化，建立该系统的Solidworks三维实体模型和ANSYS有限元模型，通过静力学和初步动力学分析,得到主轴的静态刚度、前四阶固有频率和振型图，又通过Harmonic谐响应分析得到主轴前端在一系列激振下的动态响应。通过仿真结果与初始设计参数相比较发现：该电主轴设计合理，动、静态性能基本达到指标要求。为进一步提高仿真分析的可靠性，接下来的工作是对主轴进行相关实验，检测其关键部位的实验数据，结合实测数据再进行分析。

[1]张行，陶征.基于ANSYS的铣削电主轴静动态性能分析[J].制造技术与机床，2011(1):70-73.

[2]余伟炜，高炳军. ANSYS在机械与化工装备中的应用[M].北京：中国水利水电出版社, 2006:102-116.

[3]何庆中，王明超，赵献丹.基于Solidworks Sinulation码垛机械手末端执行器导杆静力学分析[J].四川理工学院学报：自然科学版，2011,24(1)：109-112.

[4]梁双翼. 加工中心关键功能部件静动态特性分析[D]. 武汉: 华中科技大学,2006.

[5]郭大庆, 吴玉厚.陶瓷轴承电主轴主轴的振动模态分析[J]. 机电产品开发与创新, 2006,19(1):7-8.

[6]张珂，佟俊，吴玉厚，等. 陶瓷轴承电主轴的模态分析及其动态性能实验[J]. 沈阳建筑大学学报, 2008, 24(3): 490-493.

[7]吴化勇. 高速切削系统动态特性研究[D]. 青岛: 山东大学, 2005.

[8]张良. 高性能数控机床主轴部件动态分析与实验[D]. 重庆: 重庆大学, 2007.