流体静压型机械密封轴向振动特性分析

朱维兵1，周 刚1，张海洋1，夏 英

(1.西华大学机械工程与自动化学院，四川 成都 610039;2.四川大学国家大学科技园发展有限公司，四川 成都 610065)

在提倡低碳能源的今天，核电能作为一种清洁能源正迎来新一轮的高速发展。国家也将核电建设作为中低碳经济的重要支柱。反应堆冷却剂核主泵是压水堆核电站的关键设备，其机械密封是防止核主泵内放射性物质泄漏的密封装置。密封装置性能的优劣直接关系到设备能否安全运行。流体静压密封属于非接触式机械密封，在目前国内的核电站主泵中应用最为广泛。这种密封利用外部引入的压力流或被密封介质本身，通过密封端面的压力降产生流体静压效应。流体静压型机械密封在运转时存在一定的间隙，为全液膜润滑状态。它是利用密封介质的压力推开2个密封端面，从而达到闭合力与开启力的平衡，如图1所示。

图1 静压型机械密封系统示意图

机械密封装置正常运转时，密封环上承受着弹簧力、密封介质压力和液膜压力的作用；但是系统内部或外部一些不稳定因素会导致密封环产生振动，密封性能发生变化。国外对流体静压型机械密封的动态特性研究[1-3]较早，国内对此研究则较晚。穆东波等[4]计算模拟了机械密封环的端面变形及机械密封由接触式机械密封转变为非接触式机械密封的过程；廖传军等[5]、魏琳宗[6]对核主泵密封系统的流固热耦合变形进行了较为详细的研究，但对动态特性分析不是很详细。本文旨在分析流体静压型机械密封静环端面的结构参数，如转折半径、端面锥角等，对液膜刚度、阻尼和静环振动特性的影响，以期为静压型机械密封的设计提供理论依据。

1 静环动力学方程的建立

(1)

式中：KZ、DZ(包括弹性元件和液膜)分别为刚度和阻尼的量纲—参数；ω为动环角速度；r0为静环外径；C0为静环处于稳定状态时的液膜厚度；Ri为静环内径ri的量纲—参数；μ为端面流体液膜的黏度。

静环轴向振动方程

(2)

式中：m=m*ω2C0/(Sr02)为静环质量m*的量纲—参数；Ff=F*/(Sr02)，F*为密封介质施加在静环背面的力。

2 端面流场分析

2.1 液膜厚度

如图2、图3所示，设静环的内径、转折半径和外径分别为ri、re、ro，则平行段的膜厚

hp=C

(3)

收敛段的膜厚

hc=C+(r-re)β*

(4)

式中：C=C0+Z，Z是静环发生振动时沿轴向的位移；β*为静环端面锥角。

堤防工程原则上以原有堤防除险加固为主，参照《堤防工程设计规范》（GB 50286—1998）规定执行。对新建堤防，应根据山洪沟泄洪要求，经过比选，合理选定堤线和堤距布置，并根据山洪沟行洪断面、地形地质条件、当地材料以及占地情况，合理确定堤防结构形式。对人口密集区、沟道两岸地形狭窄、已建建筑物限制等没有条件布置土堤的地段，可采用防洪墙等形式；沟道两岸地形有条件时，可采用土堤形式。

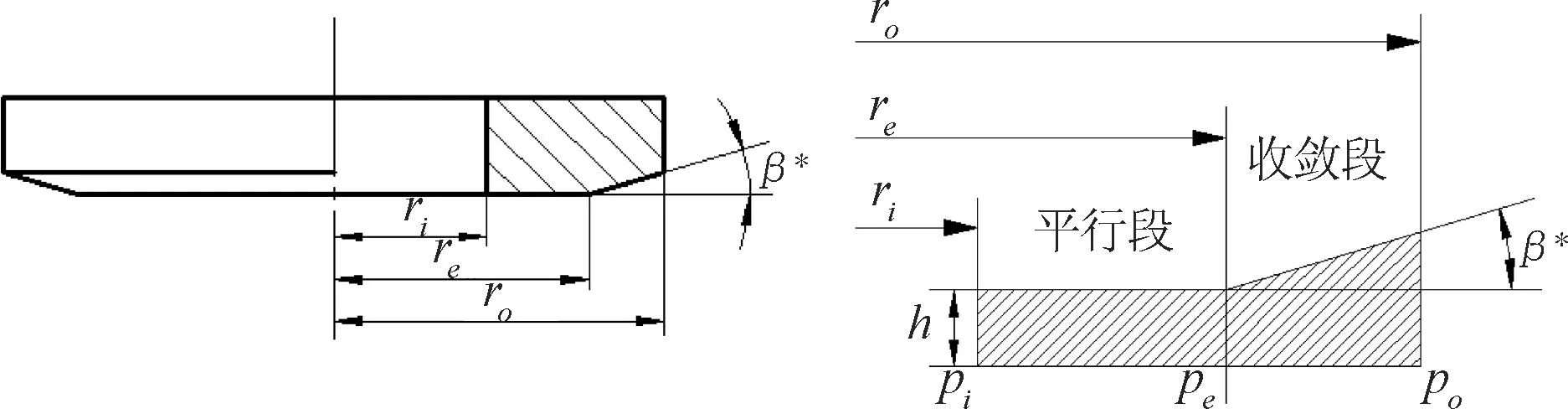
图2 静环结构示意图 图3 液膜的几何模型

2.2 液膜压力

为讨论问题方便，作以下假设： 1)液膜厚度很小，故可认为液膜压力沿厚度方向没有变化； 2)流场流动类型为层流，不存在紊流； 3)流体液膜满足牛顿黏性定律； 4)不考虑流体膜的汽化现象和密封环端面粗糙度的影响；5)不考虑流体膜所受的挤压力，膜压沿周向没有变化。

基于上述的假设条件，可得到流体静压型机械密封的膜压微分方程[2,7-8]为

(5)

边界条件为：p=pi(r=ri)，p=pe(r=re)(平行段)；p=po(r=ro)；p=pe(r=re)(收敛段)。式中：p为液膜压力；pi、pe、po分别为静环内径、转折半径和外径处的液膜压力。

对于平行段液膜，由于膜厚沿径向为一常数，故膜压微分方程(5)可简化成

(6)

对于收敛段液膜，膜厚与半径有关，得到膜压微分方程为

(7)

结合边界条件，积分方程(6)和(7)得到2段膜压的解析表达式：

pp=pi+[(pe-pi)(r-ri)/(re-ri)]

(8)

参数pe可以根据平行段和收敛段的泄漏量相等的原理[6]进行求解。

3 静环端面结构参数对液膜刚度和阻尼的影响

密封环、液膜和弹性元件的相关已知参数如表1所示。

表1 密封环、液膜和弹性元件的物理参数

将液膜压力沿密封环平行段端面积分得到平行段的开启力Fopen,为

(9)

液膜轴向刚度和阻尼的量纲—表达式[9]如下。

1)平行段刚度和阻尼。

轴向阻尼Dfz=πRmp(1-ri/re)/3

2)收敛段刚度和阻尼。

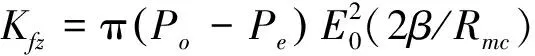
轴向阻尼Dfz=4πRmcG0

式中：Rmp=(ri+re)/2re；Rmc=(re+ro)/(2ro)；Re=re/ro；β=β*ro/C0；E0=[(1-Re)Rmc]/[2+β(1-Re)]；G0=(ln[1+β(1-Re)]-2{β(1-Re)/[2+β(1-Re)]})/[β3(1-Re)2]；Pξ=pξ/S(ξ=i,e,o)，Pξ为内径、转折半径和外径处的液膜压力的量纲—参数。

将上述相关参数带入刚度和阻尼的表达式中进行计算，得出图4和图5的液膜刚度和阻尼曲线。

图4 液膜轴向刚度

图5 液膜轴向阻尼

4 静环端面结构参数对轴向扰动的影响

图6 转折半径对静环振动特性的影响

图7 端面锥角对静环振动特性的影响

5 结论

1)图4和图5是液膜轴向刚度和阻尼随转折半径和端面锥角的变化曲线。可以看出，端面锥角越小，对刚度和阻尼的影响程度越大。由此可知，较小的端面锥角对静压特性有较大的影响。总体上说：液膜轴向刚度随着转折半径和端面锥角的增大都呈现减小趋势；液膜轴向阻尼随着转折半径和端面锥角的增大而分别呈现增大和减小的趋势。

2)图6反映的是当端面锥角为2′时，不同转折半径对静环振动衰减的影响。可以看出，转折半径为115 mm时的振动特性为弱阻尼状态；转折半径为130 mm和145 mm时的特性为过阻尼状态。由此可知，随着转折半径的增大，振动阻尼从弱阻尼向过阻尼状态转变，衰减时间延长。图7反映的是当转折半径为130 mm时，不同端面锥角对静环振动衰减的影响。可以看出，端面锥角为10′和18′时的振动特性为弱阻尼状态，端面锥角为2′的振动特性为过阻尼状态。由此可知，随着端面锥角的增大，振动阻尼从过阻尼向弱阻尼状态转变，衰减时间延长。

3)从图4至图7可以看出：端面锥角越小，刚度和阻尼越大，振动衰减时间也越短，故锥角在0至2′范围内为最佳；当转折半径越小时，若端面锥角小于2′，刚度和阻尼呈现增大趋势，振动衰减时间也越短，故当转折半径与内径重合时为最佳，此时整个静环端面都为收敛型。

[1]Green I, Etsion I. Stability Threshold and Steady-state Response of Noncontacting Coned-Face Seals[J]. ASLE Transactions, 1985，28(4): 449-460.

[2]Etsion I, Pascovici M D. Hydrodynamic Effects on the Boiling Interface in a Misaligned, Two-Phase, Mechanical Seal-A Qualitative Study[J]. Tribology Transactions, 1996，39(4): 922-928.

[3]Christophe Minet, Noel Brunetiere, Bernard Tournerie. Analysis and Modeling of the Topography of Mechanical Seal Faces[J]. Tribology Transactions, 2010,53: 799-815.

[4]穆东波，蔡纪宁，张秋翔，等. 流体静压式核电站主泵二级密封由接触式到非接触式转变的密封性能分析[J]. 润滑与密封，2009 (7): 33-36.

[5]廖传军，黄伟峰，索双富，等.核主泵机械密封的流固强耦合模型[J]. 中国科学，2011，41(12)：1649-1657.

[6] 魏琳宗. 核电站冷却剂主泵机械密封的流固热耦合研究[D]. 北京：清华大学，2010.

[7] Kuo-Shong Wang, Wei-Ren Chen. Dynamics of Clearance-Type Mechanical Seals[J]. Journal of the Chinese Institute of Engineers, 1986,9 (2) : 127-140.

[8] 刘敬喜，叶文兵，李天匀，等. 机械密封端面的膜压分布分析[J]. 石油化工设备，2007，36(5)：43-45.

[9]Green I, Etsion I. Fluid Film Dynamic Coefficients in Mechanical Face Seals[J]. ASME Transactions, 1983，10(2): 297-302.

[10]闻邦椿，刘树英，张纯宇.机械振动学[M].北京：冶金工业出版社，2011：23-45.