矩形脉冲激励下斜支承系统易损件的破损评价

段宁宁，陈安军,2

(1.江南大学 包装工程系,江苏 无锡214122；2.国家轻工业包装制品质量监督检测中心,江苏 无锡214122)

矩形脉冲激励下斜支承系统易损件的破损评价

段宁宁1，陈安军1,2

(1.江南大学 包装工程系,江苏 无锡214122；2.国家轻工业包装制品质量监督检测中心,江苏 无锡214122)

以考虑易损件的斜支承系统为研究对象，建立矩形脉冲激励下系统无量纲非线性冲击动力学方程。以脉冲激励幅值与易损件加速度响应峰值之比作为系统无量纲临界加速度，临界加速度与无量纲脉冲时间乘积为系统无量纲临界速度，引入系统支承角或频率比或质量比，构建斜支承系统易损件破损边界曲面。利用龙格—库塔数值分析方法求解方程，分析讨论频率比、质量比、支承角等因素对易损件破损边界的影响。研究表明，增大频率比、减小系统支承角、增大质量比等可增加易损件安全区域；随无量纲脉冲激励幅值增加，易损件破损区域减小。研究结论为斜支承系统的设计提供理论依据。

振动与波；易损件；斜支承系统；矩形脉冲；破损边界

自上世纪六十年代，斜支承系统应用于精密仪器设备的减振保护，且减振效果优于线性系统。文献[11，12]建立了斜支承系统的竖向非线性振动控制方程，分析了支承角、初始振幅等对系统自振的影响。文献[13]建立了基础位移激励下斜支承系统的几何非线性振动方程，讨论了基础位移激励振幅、激励频率、支承倾角等因素对斜支承弹簧减振系统非线性振动的影响。文献[14，15，16]研究了半正弦波等典型脉冲激励下斜支承系统的冲击特性，探讨了系统加速度响应，二维冲击响应谱或三维冲击响应谱及其影响因素，但未考虑易损部件。文献[17，18]虽然考虑易损件，但研究的是系统振动特性或二维冲击响应谱。目前，针对考虑易损件斜支承系统，尚未涉及到典型脉冲激励下易损件的破损评价。

以考虑易损件的斜支承系统为研究对象，建立系统在矩形脉冲激励下的无量纲非线性冲击动力学方程，运用四阶龙格-库塔法，研究系统易损件的破损边界，探讨分析系统支承角、频率比、质量比、脉冲激励幅值等因素对易损件破损边界的影响，研究结果进一步为斜支承系统设计提供理论价值。

1 无量纲冲击动力学方程

考虑易损件的斜支承系统力学模型如图1所示，易损件及包装主体的质量分别记为m1、m2，易损件与主体间的连接刚度为k1，斜支承弹簧的刚度和原长分别为k2、l0，弹簧未变形时支承角为φ0。

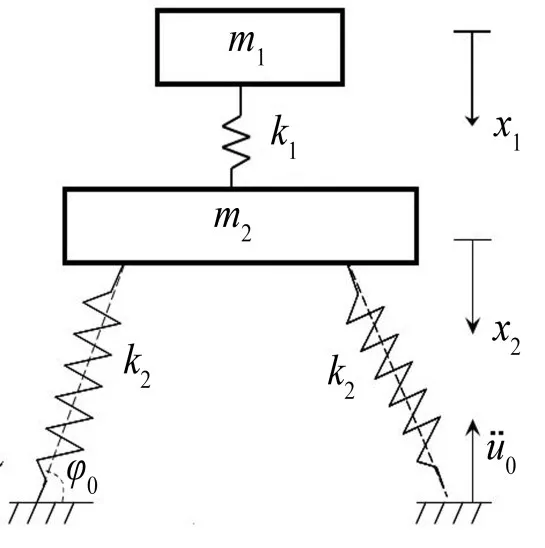
图1 斜支承系统力学模型

取系统静平衡位置为坐标原点，竖直向下为正方向，竖直方向系统自振动力学方程[17，18]

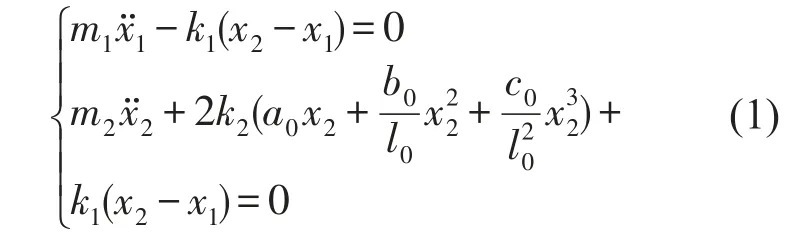
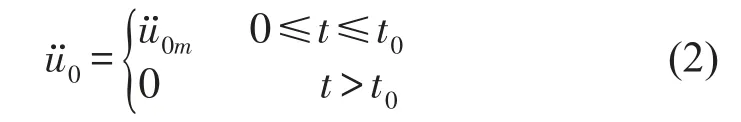
式中t0为脉冲激励时间。由式（1）、（2），系统冲击动力学方程

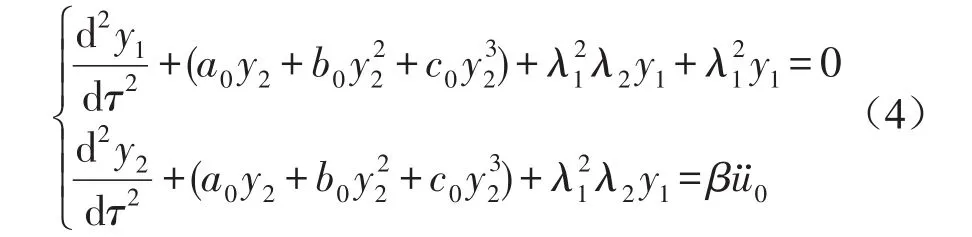
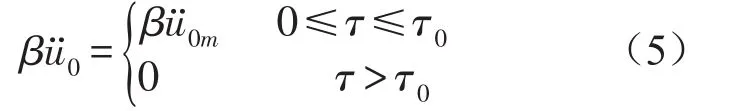
由式（4），系统解与系统支承角、无量纲脉冲激励幅值、系统质量比、系统频率比等因素有关。

2 易损件破损评价

系统易损件破损评价可为产品优化包装设计提供理论依据，传统的破损评价理论[1]主要研究单自由度系统。将包装产品处理为考虑易损件的二自由度系统，并探讨破损评价方法，更贴近实际。1易损件二维破损边界曲线

2.表示系统无量纲临界加速度，由引入的无量纲位移参数y1、y2，结合式（4），得

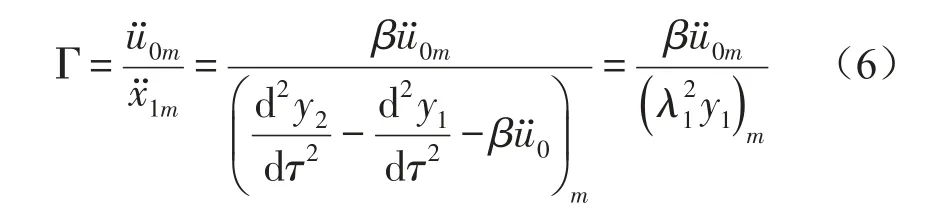
以临界加速度与无量纲脉冲激励时间的乘积V=τ0Γ表示系统无量纲临界速度，构建斜支承系统易损件的二维破损边界曲线，评价易损件破损特性。采用龙格—库塔数值分析求解动力学方程（4），分析系统支承角、质量比、频率比以及无量纲脉冲激励幅值等对易损件破损边界的影响。

支承角φ0=800，质量比λ2=0.01，无量纲脉冲激励幅值 βu¨0m=0.15时，不同频率比（λ1=10，5，3,2）易损件破损边界曲线如图2所示。由图知，破损边界曲线对频率比敏感，随频率比的增加，临界速度右移明显，安全区域显著增大。

图2 频率比对易损件破损边界的影响

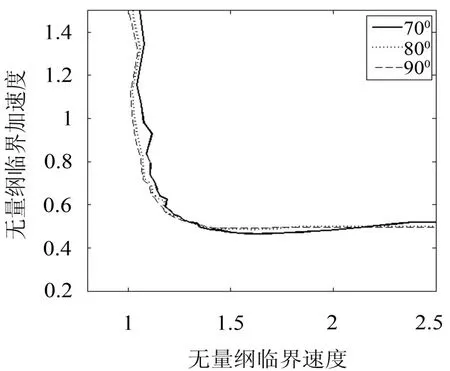
图3 支承角对易损件破损边界的影响

取λ1=10，λ2=0.01，βu¨0m=0.15，不同支承角（φ0=700,800,900）易损件破损边界曲线，如图3所示。由图知，与线性系统（φ0=900）相比，随支承角减小，安全区域有所增大。

取φ0=800，λ1=10，λ2=0.01，不同无量纲脉冲激励幅值（βu¨0m=0.01,0.05,0.1,0.15）易损件破损边界，如图4所示。结果表明，无量纲脉冲激励幅值增加，安全区有所增大。

当 φ0=800，λ1=10，βu¨0m=0.15时，质量比（λ2=0.01,0.05,0.1,0.2）对易损件破损边界影响，如图5所示。增大质量比，可增加易损件安全区。

2.2 易损件三维破损边界曲面

图4 无量纲脉冲激励幅值对易损件破损边界的影响

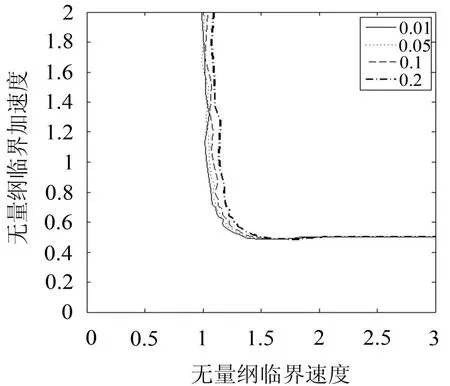
图5 质量比对易损件破损边界的影响

为全面评价频率比、支承角、质量比等对易损件破损特性的影响，取系统无量纲临界加速度Γ，系统无量纲临界速度V、频率比λ1，或无量纲临界速度V、支承角φ0，或无量纲临界速度V、质量比λ2，构建易损件三维破损边界曲面。

取质量比 λ2=0.01，无量纲脉冲激励幅值βu¨0m=0.1，不同支承角易损件破损边界曲面如图6所示，减小支承角可有效拓展易损件安全区；图7给出，当λ2=0.01，φ0=800时不同无量纲脉冲激励幅值易损件破损边界曲面，由图知，随无量纲脉冲激励幅值的增大，易损件安全区增大；φ0=800，βu¨0m=0.1，不同质量比易损件破损边界曲面，如图8所示，增加质量比，易损件安全区增大。进一步探讨系统支承角φ0对易损件破损边界曲面影响，取系统无量纲临界加速度Γ、系统无量纲临界速度V、支承角φ0作为变量，当无量纲脉冲激励幅值βu¨0m=0.1，质量比λ2=0.01时，不同频率比易损件破损边界曲面，如图9所示，随支承角减小，易损件破损边界安全区增加。进一步分析质量比λ2对易损件破损边界曲面影响，取无量纲临界加速度Γ、无量纲临界速度V、质量比λ2作为变量，当无量纲脉冲激励幅值βu¨0m=0.1，支承角φ0=800时，不同频率比易损件破损边界曲面，如图10所示，随质量比增加，安全区增大。

3 影响因素分析及结论

（1）频率比的影响。由图2、图6—图10知，易损件破损边界对频率比敏感，随着频率比的增加，破损区域减小，安全区域增大。在允许的条件下应尽量增加系统频率比（建议λ1＞5），系统设计中控制频率比对提高斜支承系统易损件的抗冲击特性具有重要意义；

（2）支承角的影响。由图3、6、9知，在给定质量比的条件下，与线性系统（φ0=900）相比，在一定范围内（700≤φ0＜900），随支承角减小，易损件破损边界的安全区增大，且在较高频率比时更加明显；

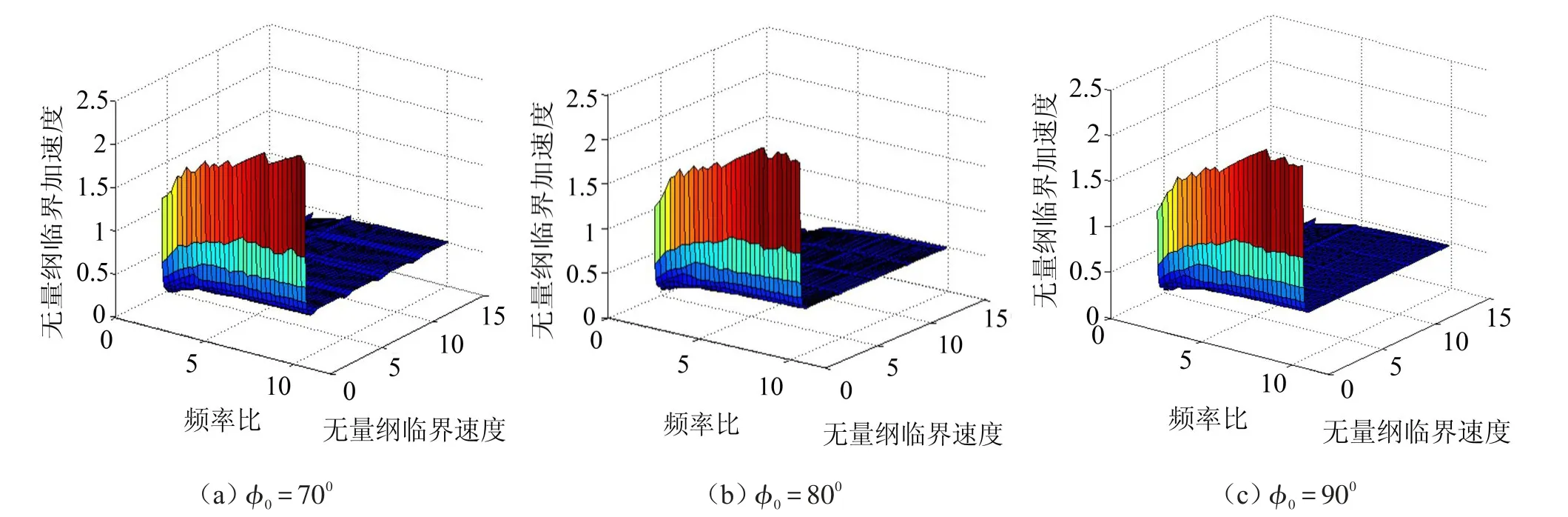
图6 不同支承角易损件破损边界曲面

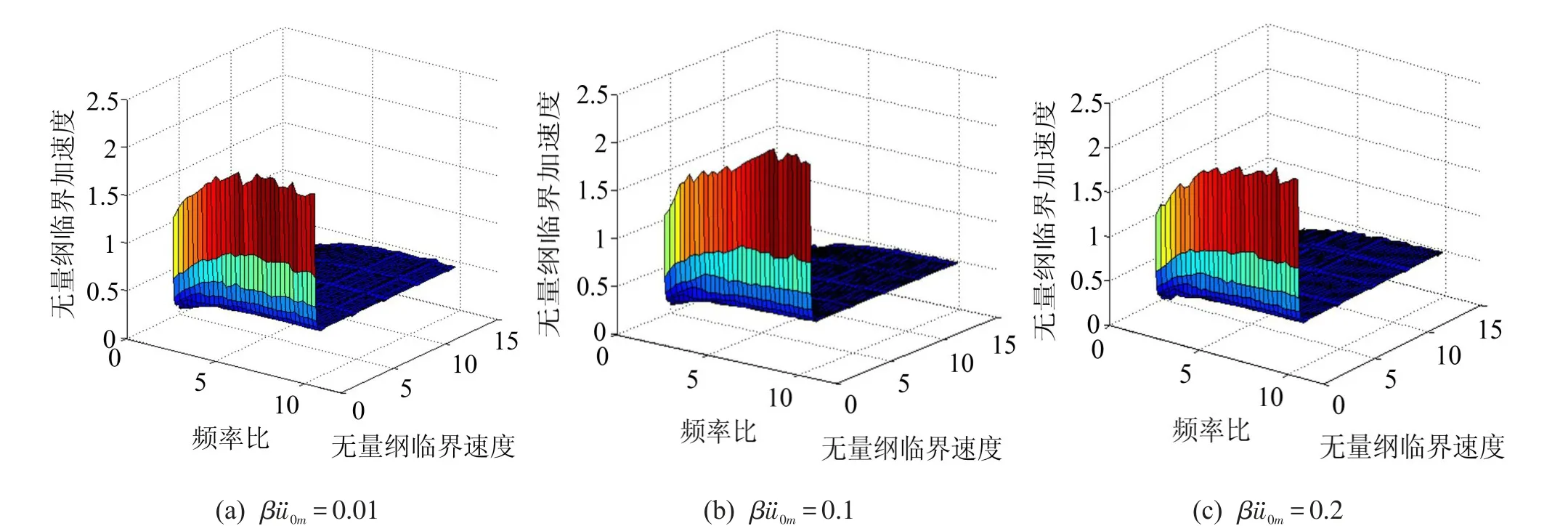
图7 不同无量纲脉冲激励幅值易损件破损边界曲面

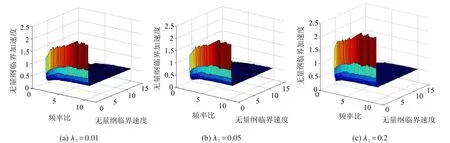
图8 不同质量比易损件破损边界曲面

（3）脉冲激励幅值的影响。由图4、7知，在给定质量比及系统支承角的条件下，较高频率比时（λ1＞5），随无量纲脉冲激励幅值βu¨0m增加，易损件临界加速度基本稳定在0.5左右，脉冲激励时间增加时，系统临界速度右移，易损件安全区增大。当脉冲激励幅值u¨0m一定，增加系统特征参数β可改善易损件抗冲击特性；

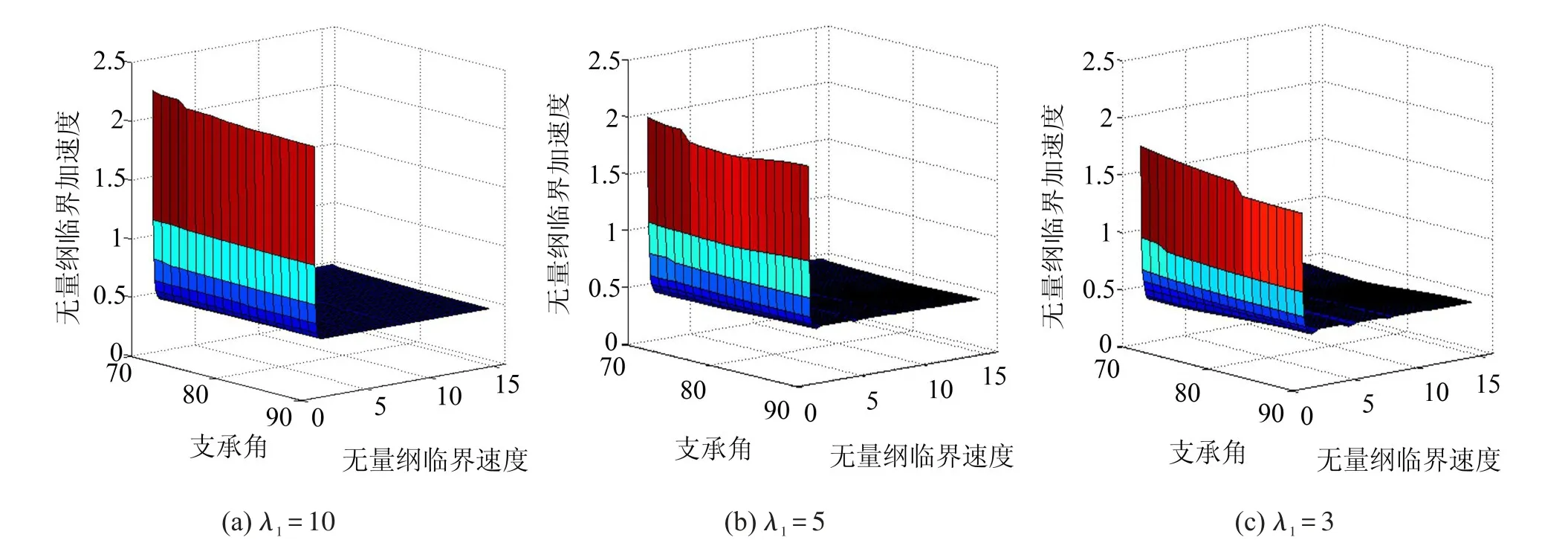
图9 不同频率比易损件破损边界曲面

图10 不同频率比易损件破损边界曲面

（4）质量比的影响。由图5、8、10知，增加质量比可使易损件安全区域增加。

对斜支承系统，通过无量纲临界加速度、临界速度，引入系统支承角或频率比或质量比，构建易损件破损边界曲面，评价易损件破损特性及相关影响因素，使得破损评价描述更为清晰。研究表明系统频率比是设计中关注的重要参数，尽可能增加频率比。相关结论可为斜支承系统缓冲设计提供理论依据。

[1]Newton R E.Fragility assessment theory and test procedure[R].MontereyResearchLaboratory,Inc.Monterey,California,1968.

[2]汤伯森.后峰锯齿脉冲的产品破损边界曲线的方程[J].振动工程学报，1990，3(4)：25-30.

[3]吴浩然，王振林，应祖光，等.半正弦波冲击时立方非线性产品包装损坏边界曲线[J].包装工程，1996，17(4)：5-8.

[4]卢富德，高 德，梁爱锋.立方非线性双层包装在矩形方波冲击下破损边界曲线的研究[J].包装工程，2008，29(12)：7-10.

[5]WANG Zhi-wei,HU Chang-ying.Shock spectra and damageboundarycurvesfornonlinearpackage cushioningsystem[J].PackagingTechnologyand Science,1999,12(5):207-217.

[6]WANG Zhi-wei.Shock spectra and damage boundary curves for hyperbolic tangent cushioning system and their important features[J].Packaging Technology and Science, 2001,14:149-157.

[7]王 军.产品破损评价及其防护包装动力学理论研究[D].无锡：江南大学包装工程系，2009.

[8]王 军，卢立新，王志伟，等.矩形脉冲激励下正切型包装系统关键部件破损曲面研究[J].包装学报，2010，2 (1)：14-17.

[9]王 军，王志伟.考虑易损件的正切型包装系统冲击破损边界曲面研究[J].振动与冲击，2008，27(2)：166-167.

[10]高 德，卢富德.考虑转动的双曲正切与正切组合模型缓冲系统冲击响应研究[J].振动工程学报,2012,25(1): 6-11.

[11]吴 晓，罗佑新，吴 扬.斜支承弹簧减振系统竖向非线性自振研究[J].振动与冲击，2008，27,(8)：85-87.

[12]陈安军.斜支承弹簧包装系统非线性振动特性分析[J].包装工程，2009，30(11)：20-22.

[13]吴 晓，罗佑新，杨立军.基础位移激励下斜支承弹簧减振系统的振动[J].振动与冲击，2009，(11)：115-117.

[14]孔凡玲，陈安军.半正弦脉冲激励下斜支承包装系统冲击特性的研究[J].包装工程，2011，(19)：47-49.

[15]孔凡玲，陈安军.半正弦波脉冲激励下斜支承系统冲击特性[J].噪声与振动控制，2012，(2)：41-44.

[16]陈安军.矩形脉冲激励下斜支承弹簧系统冲击特性的研究[J].振动与冲击，2010，29(10)：225-227.

[17]许佩霞.考虑易损件的斜支承包装系统振动特性的研究[J].包装工程，2011，(19)：5-7.

[18]陈安军.半正弦脉冲激励下斜支承系统易损件冲击特性[J].噪声与振动控制，2012，(3)：63-66.

Damage Evaluation of Tilted Support Spring System with Critical Components under theAction of Rectangular Pulse

DUAN Ning-ning1,CHEN An-jun1,2

(1.Department of Packaging Engineering,Jiangnan University,Wuxi 214122,Jiangsu China; 2.China National Control and Test Center for Packaging Quality,Wuxi 214122,Jiangsu China)

The dimensionless nonlinear dynamic equations of tilted support spring system with critical components under the action of rectangular pulse are established.To evaluate damage characteristics of the critical components,a concept of damage boundary surface is proposed.The ratio of the peak pulse acceleration to the maximum shock response acceleration of the critical components is regarded as the dimensionless critical acceleration of the system,and the product of the dimensionless critical acceleration and the dimensionless pulse duration is regarded as the dimensionless critical velocity.The angle of the tilted support,frequency ratio and mass ratio of the system are introduced as three parameters to construct the damage boundary surface for the tilted support system.Runge-Kutta method is used to solve the equations numerically.The influences of frequency ratio,mass ratio,and the tilted angle of the system on the damage boundary surface of the critical components are discussed.The results demonstrate that increasing the frequency ratio,decreasing the angle of the tilted support or increasing the mass ratio can enlarge the safety zone of the critical components,and with the increase of the dimensionless peak pulse acceleration,the damage zone of the critical components will reduce.The numerical results provide an academic foundation for design of tilted support spring systems with critical components.

vibration and wave;critical components;tilted support spring system;rectangular pulse;damage boundary

1006-1355(2014)03-0073-05

A

10.3969/j.issn.1006-1335.2014.03.015

Newton[1]提出的破损边界理论是指导缓冲包装设计的重要依据。汤伯森[2]通过产品冲击试验分析易损件加速度响应，探讨易损件最大加速度与脉冲激励的关系，研究了后峰锯齿脉冲的冲击谱和产品破损边界曲线。文献[3、4、5、6]针对非线性包装系统，建立典型脉冲激励下的动力学模型，讨论了质量比、阻尼比等对产品破损边界曲线及冲击谱的影响。王军[7]以典型线性及非线性包装系统为研究对象，研究了基于关键部件的包装系统冲击谱和破损边界，并探讨其影响因素，且以产品运输包装系统为对象，建立了系统动态逆子结构分析模型。王军、王志伟[8，9]等以正切型包装系统为例，建立了二自由度非线性系统动力学方程，分析了频率比、脉冲激励幅值、系统参数等对关键部件破损边界的影响。文献[10]建立与实际情况接近双曲正切与正切组合模型，研究转动与平动耦合冲击情况下系统的响应特性。

2013-09-20

段宁宁（1988-），女，山东济南人，硕士生，主攻运输包装。

E-mail:dnnbird@126.com

陈安军（1962-），男，河南潢川人，教授，主要从事包装动力学、机器人动力学及控制的研究。

E-mail:caj62@163.com