高等几何对初等几何教学的指导意义

广东金丹

引言

高等几何是高等师范院校数学教育专业的主干课程之一，不少学者将它与数学分析、高等代数并称为数学教育基础课程的“三高”，其重要性不言而喻。但现实教学工作中，教师可能会因为感受不到高等几何与初等几何知识之间的直接联系，忽视高等几何而造成了初等几何与高等几何知识的脱节，无法构建起较为完整的几何知识体系。

事实上，无论是数学的哪一个分支，都遵循由浅及深的发展规律。高等几何是初等几何的承接，在知识上是初等几何的因袭和扩张，在观念上是初等几何的深化与发展[1]。在高等几何中贯穿着大量的现代数学的思想、方法和观点，不仅能扩展几何知识领域，开阔几何视野，提高个人的数学素养，还能加深教师对初等几何的理解，进而站在更高的层次灵活引导学生处理初等几何问题，这对于教师从事的数学教学工作有着极其重要而深远的影响。

高等几何对初等几何的指导意义这个论题有着非常广阔而丰富的研究空间，多年来有不少的国内外学者潜心钻研在这一问题上，而且也得到了许多精彩的结论。本文笔者借鉴前人的研究成果，尝试从高等几何课程地位和新大纲背景下对中职初等几何教学要求的角度来认识高等几何与初等几何的关系，浅谈高等几何学习对丰富初等几何研讨方法和拓宽初等几何解题途径的指导意义。

1 高等几何对初等几何教学的指导意义

1.1 高等几何和初等几何的界定与联系

在探讨高等几何对初等几何解题研究的指导作用之前，首先就本文所涉及到的高等几何和初等几何这两个概念所涵盖的范围加以限定，并简单了解其内容特点以及在克莱因群论观点下存在的内在联系，明确高等几何与初等几何之间并不是相互孤立的：初等几何是高等几何的基础，而高等几何是初等几何的延伸和拓展。

习惯上，我们把小学和中学阶段所接触的几何知识都纳入初等几何范围。初等几何以欧氏几何为理论基础，是几何学中最为基础的部分，包括空间与图形、平面解析几何、立体几何等等。初等几何所涉及的思想方法具有较强的针对性，内容相对直观，学生可以先直接采用观察、测量等实验手段了解几何图形，发现其中规律，再根据实际认知水平逐步抽象思维，完成逻辑演绎证明。而我们所说的“高等几何”通常是指在19世纪初期产生的另一几何学重要分支——射影几何。它的开辟和盛行，一方面是由于它有巨大的美学魅力，另一方面是由于它把几何作为一个整体来研究时所获得的明显效果以及它与非欧几何的紧密联系[2]。高等几何主要以克莱因的几何学群论观点为指导，他提出采用变换群对几何学进行分类，重点突出变换不变性的基本数学思想，这在几何学不同的理论体系中具有一定的普适性。结合克莱因的群论观点，我们可以这样概括：欧氏几何涵盖于射影几何，欧氏几何是射影几何的一个特例。

1.2 高等几何和初等几何的课程地位

初等几何一直都是中等职业院校数学教育的重要组成部分之一，而高等几何是高等师范院校数学教育专业的基础课程之一，初等几何与高等几何的课程开设都具有其必要性和重要性。研究高等几何知识体系的构建对中职数学教学工作产生的影响，有必要关注高等几何课程的教学目的和新大纲背景下对初等几何教学的要求。

1.2.1 高等几何的教学目的

培养具有现代数学思想，并能应用现代数学思想指导教学的数学教师，是高等师范院校数学教育的培养方向。高等几何作为高师数学专业的重要专业课程之一，是数学教育任务的重要组成部分，其课程的开设一般是安排在学习了解析几何和高等代数之后，目的是在具备一定的初等几何、解析几何和高等代数知识的基础上，系统地学习射影几何知识，引入变换群观点，抓住变换和不变性的基本数学思想。高等几何涵盖了大量现代数学思想、方法、理论、应用等，对于发展空间概念，丰富高层次的几何知识，提高数学专业素养，培养数学逻辑推理和合情推理能力具有重要作用。不仅能更深入地认识几何学，为进一步的学习微分几何、画法几何或者其他高等数学知识做好准备，还训练了抽象思维，增强了数学审美意识，加强了数学修养，提高了从师能力，为数学教学工作打下坚实的基础。

1.2.2 新教学大纲对初等几何的要求

清华大学萧树铁教授说，在我国的传统文化中，逻辑思维一直比较薄弱，数学，尤其是欧氏几何，在这方面的训练是大有可为的。著名数学家陈省身在2002年接受采访时更是强调，中学一定要讲欧氏几何，几何推理的部分不能取消，整个数学就是建立在推理之上的。2009年重新修订的《中等职业学校数学教学大纲》就是在教育形势的发展和教学改革的不断深入的大环境下应运而生的，它明确了“以服务为宗旨，以就业为导向，以提高质量为重点”的办学方针，提出本课程的任务是：使学生掌握必要的数学基础知识，具备必需的相关技能与能力，为学习专业知识、掌握职业技能、继续学习和终身发展奠定基础。新大纲将数学课程划分为基础模块、职业模块和拓展模块，在各模块间进行知识组合，在各学科间进行知识渗透。在新大纲下，培养目标已经由重点培养逻辑思维能力转向培养几何直观能力和空间想象能力，这要求教师调整教学观念和教学方法，“注意突出几何的本质，引导学生经历直观感知、操作确认、思辨论证、度量计算等探索与研究几何问题的过程，发展学生的空间观念和几何直觉”。[3]几何学的教育价值不容小觑，欧氏几何长期以来作为训练逻辑推理的素材的地位不可取代，几何对学生多种能力的塑造和培养有着至关重要的影响。

1.3 丰富初等几何研讨方法，拓宽初等几何解题途径

明确了高等几何与初等几何的关联，将有利于我们把高等几何中获得的观点、体会反馈于初等几何。事实上，将高等数学知识下放到初等数学教材中的成分越来越多，我们所熟悉的初等几何中有部分内容是需要以高等几何为理论依据的，例如平面几何的平移、旋转是在正交变换群下的合同变换；立体几何直观图的画法、截面图的作法分别是以透视仿射对应性质及笛沙格定理的理论为作图依据[4]。前苏联几何学家亚格龙曾经指出：“在初等几何中……，包含了两个重要的有普遍意义的思想，它们构成了几何学的一切进一步发展的基础，其重要性远远超出了几何学的界限。其中之一是演绎法和几何学的公理基础；另一个是几何的变换和几何学的群论基础。”可见，学生在学习初等几何的过程中，实际上也是接受高等几何数学意识和思想方法渗透的过程。利用这一特点，我们可以考虑用高等几何理论来解决部分初等几何问题，从而为初等几何研究探讨和解题方法寻求更广泛的途径[5]。另一方面，由于许多高等几何定理、命题可以给出初等几何的证明或解答，因此也可以将此类高等几何问题进行改编，创作出初等几何中的提高题、压轴题等，这无疑为教师们探索初等几何的教学和科研指明了方向。

下文将通过仿射变换寻找初等几何命题解题思路。

在高等几何中，只要经过适当的仿射变换，任意一个三角形、平行四边形、梯形或椭圆可对应变为特殊的正三角形、正方形、等腰梯形或圆形。如果所给命题在这些特殊的图形中结论成立，则根据仿射变换保持同素性、结合性、平行性、共线三点的单比不变、封闭图形的面积之比不变等性质即可推出在原命题中结论也成立[4]。

例如：将任意三角形每一顶点与对边上的三等分点相连得六条直线，求证这六条直线所围成的六边形三双对顶点的连线共点。

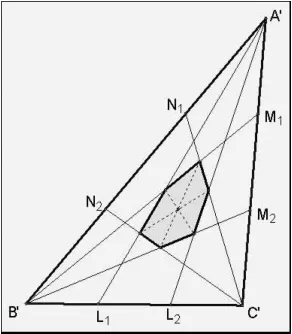
（图 1）

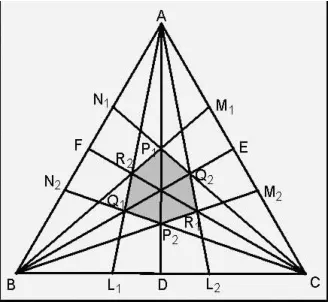
（图 2）

由于点线的结合性在仿射变换上都不变，所以可以利用仿射变换将任意三角形ΔA'B'C'（图1）变成正三角形ABC（图2），且各边的三等分点及中点对应变成正三角形各边的三等分点和中点，因而本题就正三角形的情况证之。

因此，上述命题等价于：设L1、M1、N1（i＝1，2）分别为正三角形ABC三边上的三等分点，由六条直线围成六边形P1R2Q1P2R1Q2，求证三双对顶点的连线 P1P2，R1R2，Q1Q2共点。

显然，运用高等几何的知识来处理上述题目时解法相当简单。当然这种高等解法不能直接进入中职数学课堂，但仍具有重要的参考价值，为教师思考问题指明方向，在一定程度上起到启发和诱导的作用。高等几何让我们处于更高的立足点，以更远的视野、更丰富的知识，从几何学的全局和整体来理解和把握初等几何。面对初等几何题目，我们的思路不再单一，可以尝试站在另一种角度去思考、分析和理解初等问题，以寻求更为简捷的处理方法，在不断的探索中不仅丰富了初等几何解题的途径，还可以创新初等几何问题，充分发挥高等几何对初等几何的指导作用。

[1]关丽娟.高等几何与初等几何的相融性[J].高师理科学刊,2007，9：76.

[2]R·柯朗、H·罗宾.什么是数学[M].上海：复旦大学出版社，1995.

[3]中华人民共和国教育部制订.普通高中数学课程标准（实验）[M].北京：人民教育出版社，2003.

[4]李恩凤.高等几何与初等几何的关系[J].青海师专学报,2001，6：53.

[5]刘德金,张全信.试论高等几何对初等几何的指导作用[J].德州师专学报,1997.

[6]张初荣.试谈高等几何对中学几何教学的指导作用[J].零陵师专学报,1989（第 3期）.