桥梁易损性曲线计算方法研究

张小璇 陈世鸣

(同济大学结构工程与防灾研究所，上海 200092)

1 概 述

结构易损性曲线(Fragility Curves)定义为在不同强度地震作用下结构发生破坏的概率。当某一地区的地震灾害等级确定后，该地区桥梁的易损性曲线便可以根据已知地区的地震动参数(IM)范围，计算出对应地震动参数下桥梁结构或构件地震损伤指标(DI)超过其承载力(C)的概率，表达方式如式(1)所示：

Pf=P[DI>C|IM]

(1)

计算易损性曲线的理论方法可分为两类：非线性静力方法(Nonlinear Static Procedures,简称NSP)和非线性动力方法。后者在结构底部作用实际的地震加速度，符合实际的地震反应情况，但是需要耗费大量的计算工作量和时间。而非线性静力方法是指以Pushover分析得到的荷载变形曲线为基础，计算出给定地震动下结构的最大位移。由于其避免了复杂的时程分析并且大大减少了运算量和运算时间，因此近年来受到了越来越多的发展和应用。

国内外在桥梁易损性曲线分析方面做了大量研究，如Hwang[1]、Nielson[2]、张菊辉[3]等。以往的易损性曲线的研究中，由于不同学者采用的模型参数、损坏等级以及计算方法的不同，导致即使针对同一地区桥梁，其易损性分析结果也会有很大的差别。为了克服以上不足，可采用同样的桥梁分析模型，参照同样的损坏等级，在相同的地震波作用下，使用不同的分析方法进行计算，比较分析各类方法的优缺点。

本文对常见的钢筋混凝土连续梁桥结构，采用四种非线性静力分析方法(承载力反应谱法、N2法、改进的模态Pushover法以及自适应承载力反应谱法)，结合50组地震波反应谱，计算出结构在地震作用下的易损性曲线。以非线性动力分析计算结果作为比较的标准值，研究桥梁结构易损性曲线的实用简化计算方法。由于地震对于桥梁结构在横桥向的损坏远大于其在顺桥向所造成的损坏，因此在本文的研究中选择建立三维的桥梁模型，并对其横桥向的地震响应进行分析计算。

2 易损性曲线分析流程

进行易损性曲线分析时，首先需建立桥梁样本，再根据所选取的地震波数据，采用非线性静力方法或者非线性动力方法对结构进行分析。最后根据结构不同的损坏等级的定义，判断结构在相应地震波作用下所发生的损坏及所属的损坏等级，并进行易损性曲线的计算。具体流程如图1所示。

图1 易损性曲线分析框架Fig.1 Analysis frame of fragility functions

2.1 桥梁参数选择

中等跨径多跨混凝土连续梁桥是目前已建桥梁中应用较多的一种桥型。本文以四等跨钢筋混凝土连续梁桥为研究对象，计算模型如图2所示，计算参数参考Bal等[4]给出的桥梁结构参数范围，如表1所示。

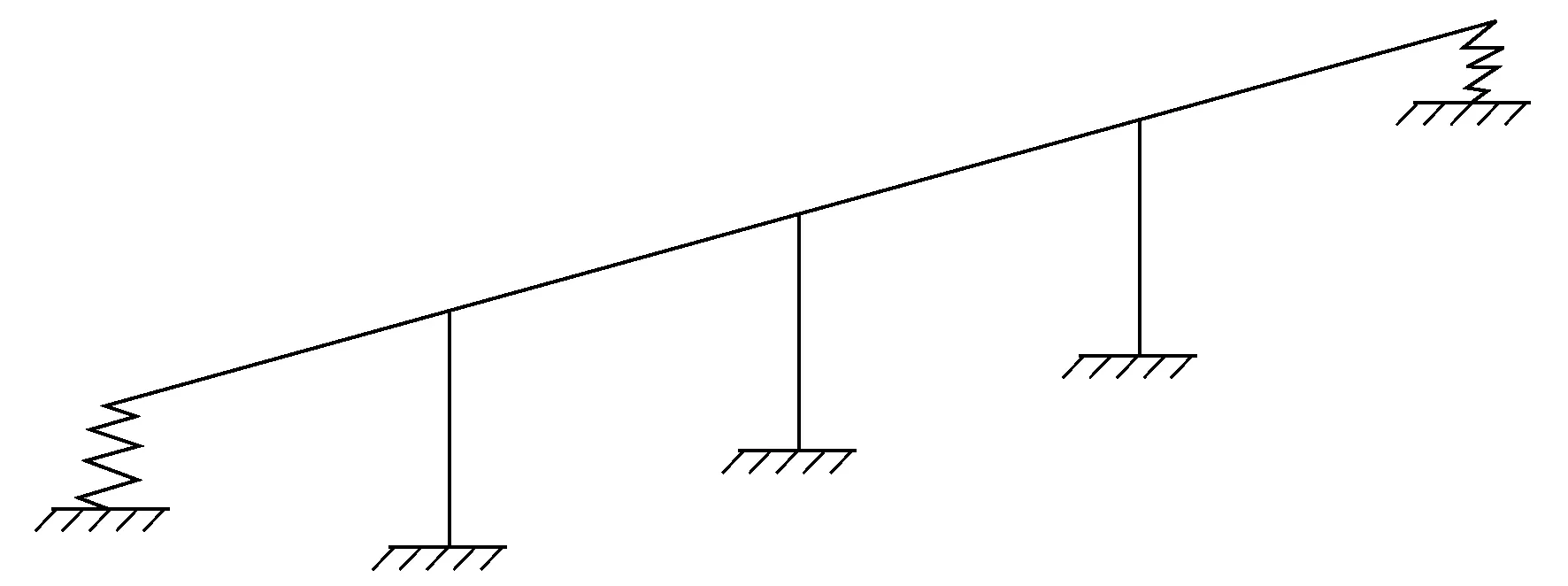
图2 桥梁构造形式Fig.2 Configuration of a bridge model

表1材料以及几何尺寸的参数列表

Table1Distributionofmaterialandgeometricalproperties

参数名称平均值Cov概率分布形式钢筋弹性模量/GPa2003%Normal钢筋屈服强度/MPa371.111%Normal混凝土强度/MPa4020%Gamma桥墩高度/m1515%Normal桥墩直径/m214%Lognormal跨度/m4022%Normal桥面板宽度/m54%Lognormal桥面梁高度/m12%Lognormal

注：Cov表示标准差与平均值的比值。

2.2 桥梁模型建立

易损性曲线的计算需要对上百个桥梁使用庞大数量的地震波进行分析，因此选择使用可以提供自动分析平台的OpenSees作为分析软件。桥梁模型使用3D环境建模，即在每个节点考虑6个自由度。桥墩使用纤维单元建模以考虑其材料非线性；混凝土模型选择多轴Kent-Scott-Park混凝土模型；钢筋模型使用的是Giuffre-Menegotto-Pinto钢筋模型。桥台使用等效刚度弹簧进行模拟，其刚度参考Casarotti等[6]给出的值26 329 kN/m。

2.3 地震波选择

本文采用的地震波是从PEER数据库选取的。为了避免因放大过程中改变了真实地震波的频率范围和持续时间而影响到地震释放能量以及频谱信息等，选取了50个没有经过任何放大的真实地震波。同时，为了避免近断层地震的复杂性，所选的地震波也尽量避开近断层地震波数据。以下列出了所选50个地震波的总体信息：

(1) 震级：5.0～7.5Mw。

(2) 距断层距离：10～150 km。

(3) 断层类型：平移断层(Strike slip)和倾斜断层(Dip-slip)。

图3表示这50个地震波的峰值加速度(PGA)分布情况。从图中可以看出这50个地震波的PGA强度从0到1 g基本呈平均分布。

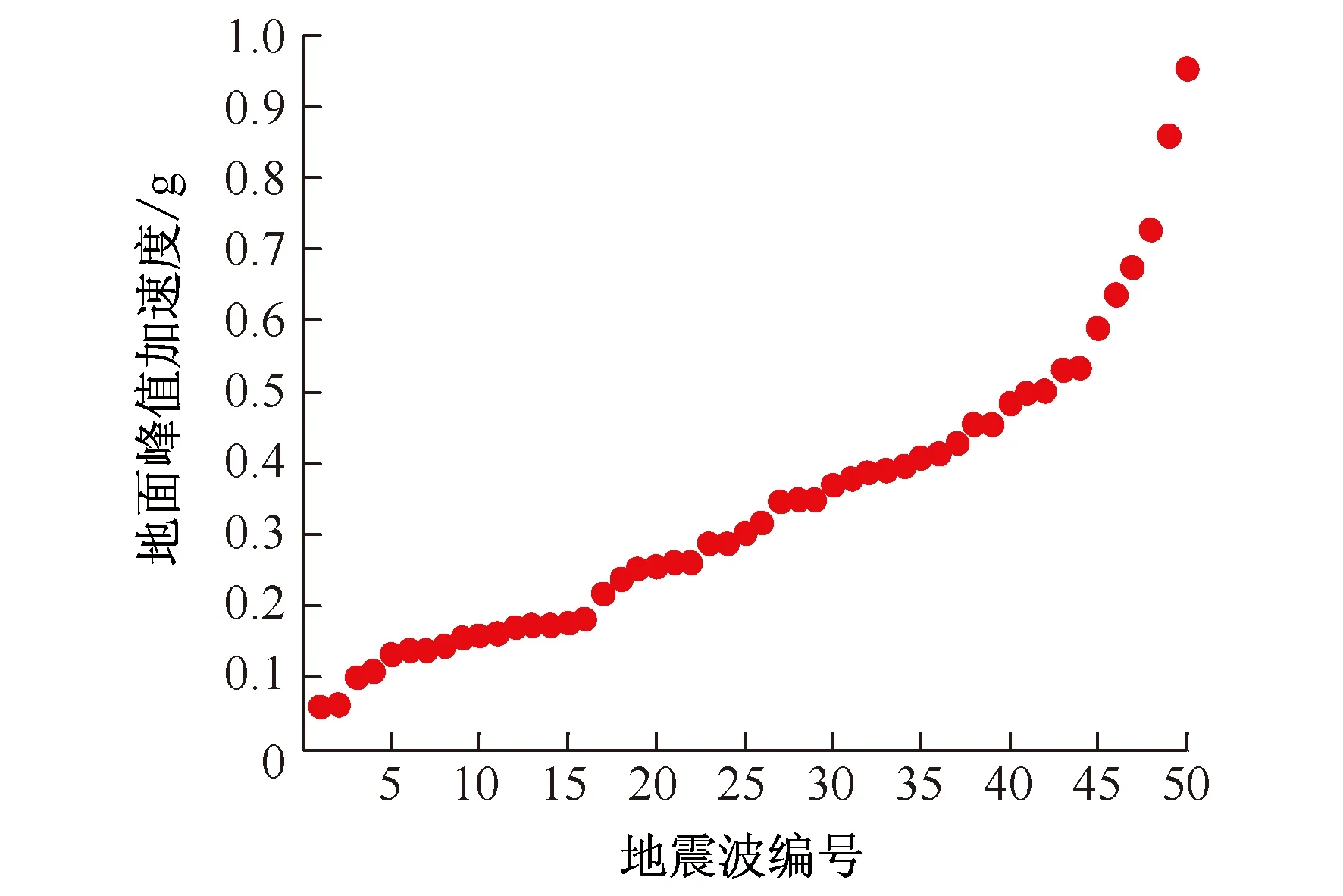
图3 50个地震波的PGA分布Fig.3 PGA distribution of the 50 ground motion records

2.4 损坏等级

参考HAZUS[5]给出的损坏等级分类，定义了轻微、中度、严重和倒塌四种损坏等级，分别用LS1，LS2，LS3和LS4表示，以Neilson[2]给出的曲率作为量化参数，每个损坏等级对应的具体数值为1.29,2.10,3.52和5.24。

位移延性比与曲率延性比可根据Priestley等[7]给出的转换公式计算，如式(2)、式(3)所示。

μΔ=1+3(μφ-1)×(lp/l)×[1-0.5(lp/l)]

(2)

lp=0.08l+9db

(3)

式中，μΔ表示位移延性比；μφ表示曲率延性比；lp表示桥墩的塑性铰长度；l为桥墩的长度；db表示为桥墩中纵向钢筋的直径。

桥梁结构整体的位移延性比取值为三个桥墩中位移延性比的最大值。

3 非线性静力分析方法

非线性静力分析方法(NSP)提供了一个以Pushover分析结果为基础，评估一个结构体系在地震作用下变形能力的平台。

由于不同静力分析方法的要求不同，对每座桥梁结构使用了三种不同的Pushover分析方法：①自适应Pushover；②均布荷载的传统Pushover；③按照第一模态阵型分布荷载的传统Pushover。其中位移控制Pushover分析的控制位移定义为结构整体位移达到0.7m或者任意桥墩受拉钢筋受拉应变达到0.1。

进行随机取样之前，对样本随机取样的结果进行了数值收敛性分析。按照表1参数范围选取了10 000座随机生成的钢筋混凝土桥梁，并对其进行Pushover分析，通过计算得到这10 000座桥梁中点最大位移的平均值，并以此结果作为准确值。然后选取不同大小的样本(从5到290)，对这些桥梁进行Pushover分析，得到每一组样本的桥梁最大位移平均值，计算每组样本的平均相对误差(图4)。从图4中可以看出，当样本大小超过170个之后，相对误差就稳定保持在4%之内。因此之后的计算分析，选择使用的样本大小为200。

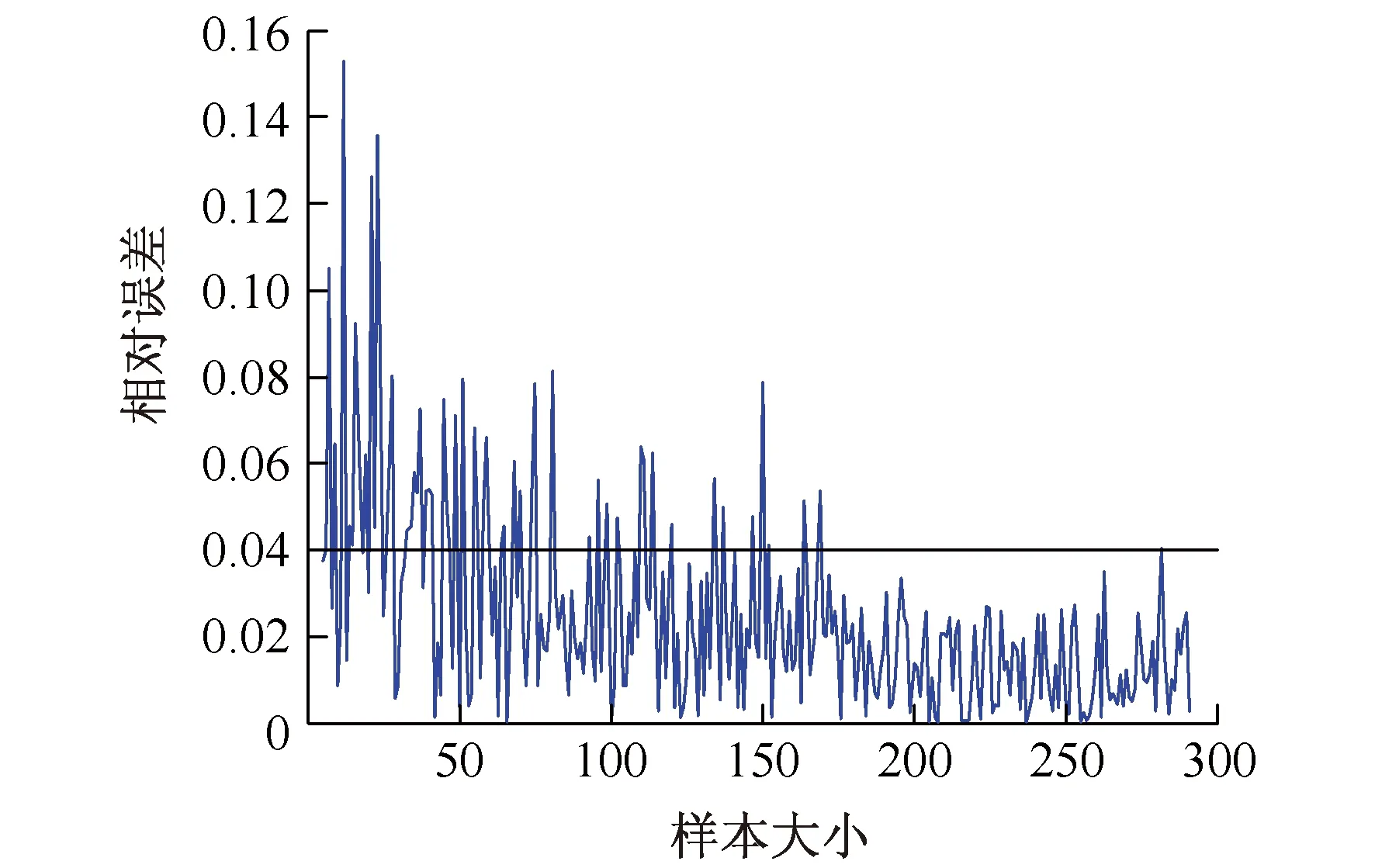
图4 平均相对误差与样本大小的关系Fig.4 Relationship between the relative error and the size of sample

本文使用的承载力反应谱法(CSM)、N2法、修改后模态Pushover法(MMPA)以及自适应承载力反应谱法(ACSM)都是以Pushover分析结果转化而成的承载力曲线为基础，根据真实地震波反应谱以及图形迭代方法估算结构在对应地震作用下的最大位移。根据桥梁结构在对应地震强度下所处的不同损坏等级评定结果，进行数值回归计算，得到易损性曲线对数正态分布的平均值λ和标准差ξ。

3.1 承载力反应谱法

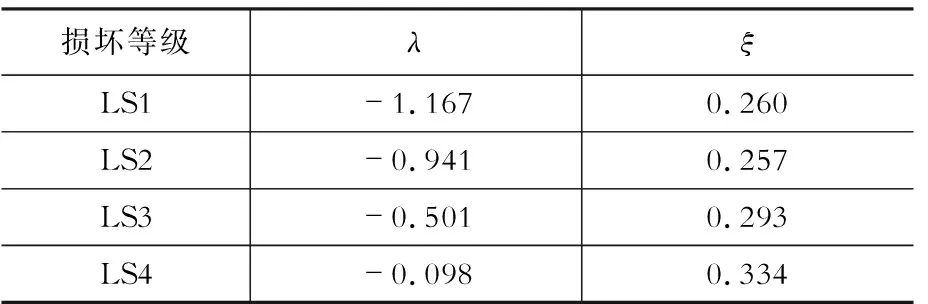
承载力反应谱法(CSM)，是一种应用图表的计算方法，可通过迭代比较结构承载力曲线与地震反应谱的关系，计算结构对应的最大位移。为了考虑结构体系的非线性性能，在迭代的过程中参照FEMA-440[13]给出的公式，计算等效阻尼以及反应谱折减系数。通过计算得到的易损性曲线对数正态分布的平均值λ与标准差ξ如表2所示。

表2CSM的对数正态分布的平均值与标准差

Table2StatisticsoffragilityfunctionsbyCSM

损坏等级λξLS1-1.167 0.260 LS2-0.941 0.257 LS3-0.501 0.293 LS4-0.098 0.334

3.2 N2法

N2方法首先是由Fajfar在1988年时提出，作为一种简单的估算结构在地震作用时的最大响应的方法，进而又在2000年时被Fajfar[8]提出改进办法。N代表非线性(Nonlinear)分析，2代表在此方法中有两个相互独立的数学运算模型，分别是Pushover分析和反应谱法。

N2与CSM在很多方面都是相似的，但N2使用非弹性反应谱而不是利用弹性反应谱乘以由等效阻尼推导而出的反应谱折减系数。除此之外，根据FEMA-356[9]，承载力双直线的屈服后刚度应等于零。通过计算得到的易损性曲线对数正态分布的平均值λ与标准差ξ如表3所示。

表3N2的对数正态分布的平均值与标准差

Table3StatisticsoffragilityfunctionsbyN2

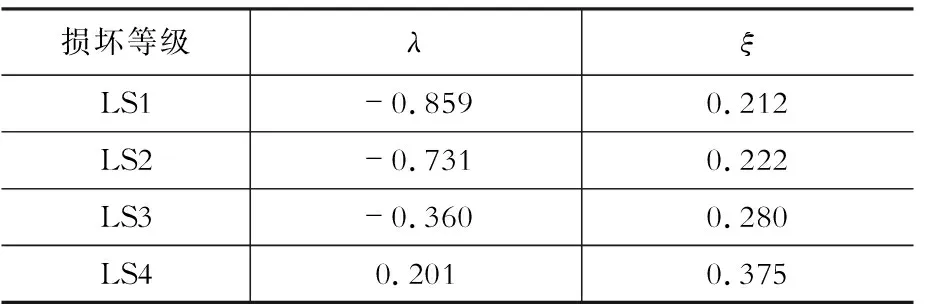
损坏等级λξLS1-0.8590.212LS2-0.7310.222LS3-0.3600.280LS40.2010.375

3.3 改进的模态Pushover分析

模态Pushover分析方法是由Chopra 和Goel在2002年提出，建议在静力分析的过程中，对每一个重要模态分别进行非线性静力分析。此方法在提出后被广泛地应用在工程和学术领域。近期，Chopra 和Goel[10]经过研究提出，在一般地震作用下桥梁的高阶模态的响应通常都保持在弹性范围内，因此对于高阶模态的分析应当直接使用弹性反应谱。因此他们提出了改进的模态Pushover分析方法。改进的部分是非弹性反应谱只是在第一模态的非线性静力分析中使用，对于高阶模态，假设整个结构处于弹性范围。通过计算得到的易损性曲线对数正态分布的平均值λ与标准差ξ如表4所示。

表4MMPA的对数正态分布的平均值与标准差

Table4StatisticsoffragilityfunctionsbyMMPA

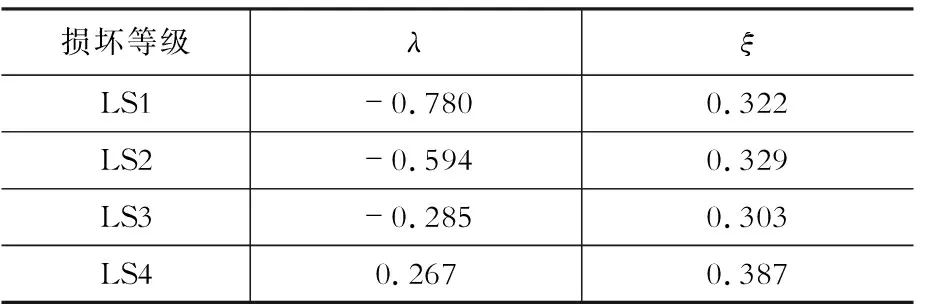
损坏等级λξLS1-0.780 0.322 LS2-0.5940.329 LS3-0.2850.303 LS40.2670.387

3.4 自适应承载力反应谱法

与以往非线性静力学分析方法不同，自适应承载力反应谱法(ACSM)不再需要使用多自由度体系的任何弹性或者非弹性振动模态来计算其等效单自由度(SDOF)体系，而是等效的SDOF自适应承载力曲线在每一步的加载中根据真正的变形和刚度变化计算得来的[11]。ACSM中一个非常关键的问题便是反应谱折减系数的定义，然而在此方法中并没有严格的介绍需要遵循的计算公式。在这些阻尼方法中，Priestley等[12]提出的方法被认为是可以给出最精确的结果，其中计算公式如式(6)、式(7)所示：

(6)

(7)

通过计算得到的易损性曲线对数正态分布的平均值λ与标准差ξ如表5所示。

表5ACSM的对数正态分布的平均值与标准差

Table5StatisticsoffragilityfunctionsbyACSM

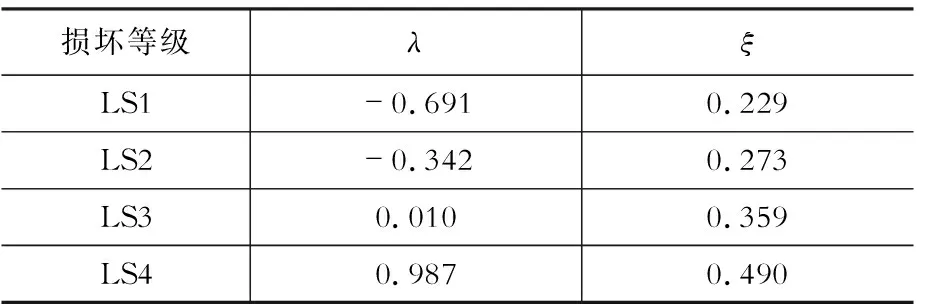
损坏等级λξLS1-0.691 0.229 LS2-0.342 0.273 LS30.010 0.359 LS40.987 0.490

4 非线性动力方法

非线性动力方法是估算一个结构在地震中变形最准确的方法。因此非线性动力方法可作为计算结果的标准值，与其他非线性静力方法进行比较。使用OpenSees进行非线性时程分析。通过计算得到的易损性曲线对数正态分布的平均值λ与标准差ξ如表6所示。

表6NLTHA的对数正态分布的平均值与标准差

Table6StatisticsoffragilityfunctionsbyNLTHA

损坏等级λξLS1-0.870 0.242LS2-0.626 0.271 LS3-0.309 0.309 LS40.146 0.382

5 结果分析

与非线性时程分析的结果比较，图5表示对于每一级损坏等级的易损性曲线。

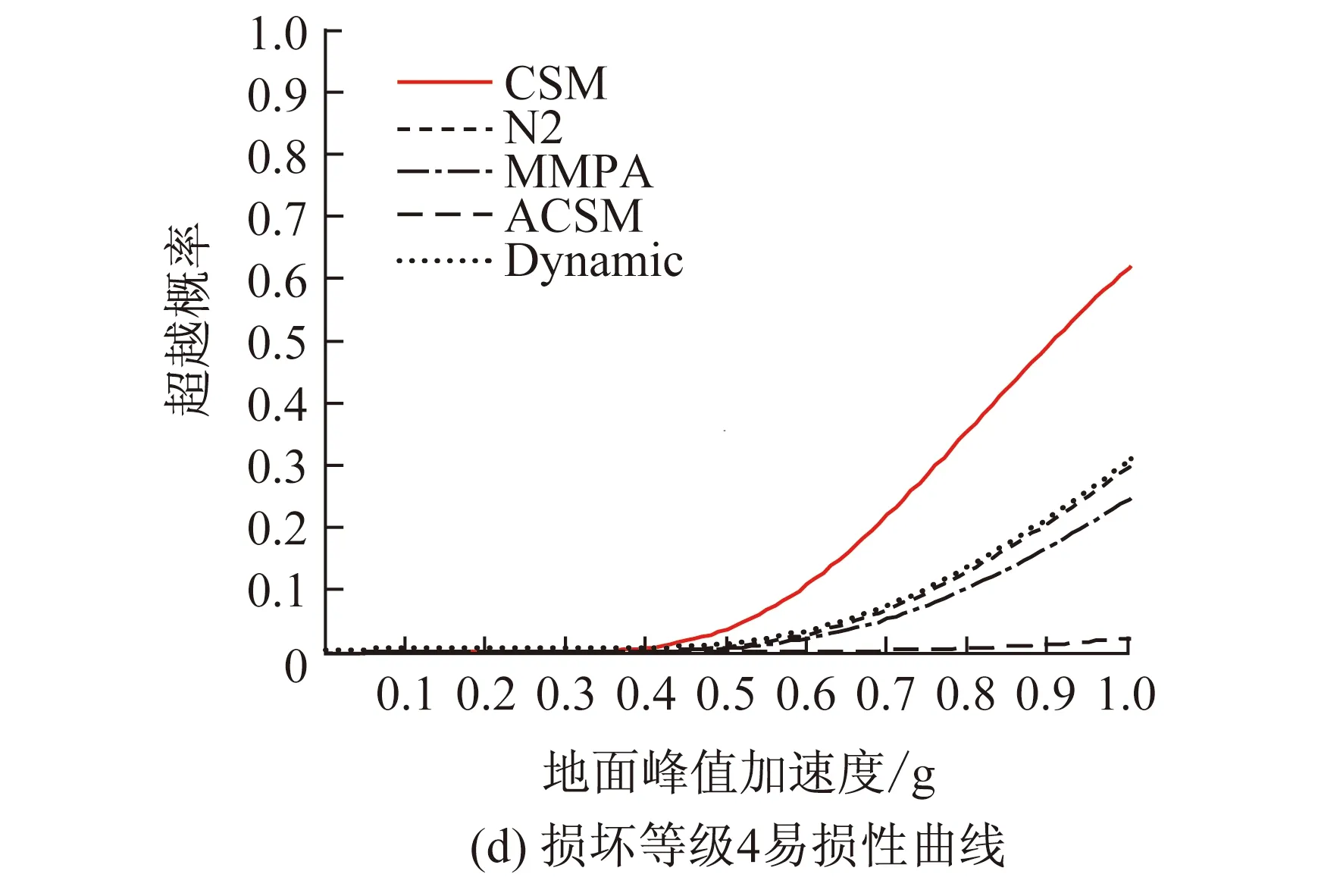
图5 每一级损坏等级的易损性曲线Fig.5 Fragility functions for each damage state

从图5中可以看出，N2是最接近动力学结果的，紧接其后的便是MMPA。二者都没有涉及等效阻尼的计算，使用的是非线性反应谱的概念。

ACSM虽然使用了自适应的Pushover分析，但是并没有给出更好的结果。可能的原因是其使用的等效黏滞阻尼计算公式在相对较小的地震波作用下，不能给出相对准确的等效阻尼值，从而导致计算得出的反应谱折减系数不准确。CSM也没有提供很好的预测结果，在易损性曲线中CSM却给出了比动力分析结果要高的值，其原因可能是，CSM使用的等效阻尼计算公式与ACSM中使用的不同，而在过小的地震波作用下，CSM的阻尼计算会导致估算的等效阻尼比实际值偏小，从而导致最终结果偏大。在非线性静力分析中造成误差的另一个原因是由于所有的分析计算都是自动生成的，因此当不规则地震波反应谱与结构承载力曲线相交多于一个交点时，使用的是Casarotti等[6]建议的第一个交点，而在强度较小地震波作用时，会造成误差。

6 结 论

本文以动力分析结果为标准值，比较了非线性静力方法(承载力反应谱法、N2法、改进的模态Pushover分析法以及自适应承载力反应谱法)在计算钢筋混凝土连续梁结构的地震作用易损性曲线的特点。

承载力反应谱法在最初的设计中主要针对房屋建筑结构，虽然FEMA-440[13]中给出的相应参数的完善，但其结果仍旧不理想。

自适应承载力反应谱法克服了以往非线性静力方法无法考虑到结构在地震作用下进入非线性阶段后的结构刚度退化和内力重分布影响的缺点，自适应Pushover分析可得到更准确的结构承载力反应谱。但是由于ACSM在计算过程中使用了等效阻尼的方法，因此在小强度地震作用下，计算结果的准确度受到影响。

N2法计算过程中使用的是非线性反应谱，因此无论是小强度地震还是高强度地震，都可以给出高准确度的计算结果。紧随其后便是改进的模态Pushover分析法。

综上所述， 在钢筋混凝土连续梁桥结构易损性曲线计算中，N2法给出了计算精确度和计算效率之间最好的平衡，不仅缩短了计算时间，而且又提供了最接近非线性时程分析的结果。

致谢感谢帕维亚大学ROSE School, EUcenter, GEM对本文第一作者在帕维亚大学学习期间的资助以及对本文研究给予的技术支持。

[ 1 ] Hwang H, Liu J B, Chiu Y. Seimic fragility analysis for highway bridges [R]. Individual study, Center for Earthquake Research and Information, University of Memphis, USA, 2001.

[ 2 ] Nielson B G, DesRoches R. Seismic fragility methodology for highway bridges using a component level approach [J]. Earthquake Engineering and Structural Dynamics, 2007,26(6): 823-839.

[ 3 ] 张菊辉.基于数值模拟的规则桥梁墩柱的地震易损性分析[D].上海：同济大学，2006.

Zhang Juhui. Seismic fragility analysis of regular bridge piers based on numerical simulations [D]. Shanghai: Tongji University, 2006. (in Chinese)

[ 4 ] Bal I E, Crowley H, Pinho R. Displacement-based earthquake loss assessment: method development and application to Turkish building Stock [R]. ROSE Research Report, IUSS Press, Pavia, Italy, 2010.

[ 5 ] HAZUS. Multi-hazard Loss Estimation Methodology Earthquake Model [M]. Federal Emergency Management Agency, Washington D C, USA, 2003.

[ 6 ] Casarotti C, Pinho R, Calvi G M. Adaptive Pushover-based methods for seismic assessment and design of bridge structures [R]. ROSE Research Report No. 2005/06, IUSS Press, Pavia, Italy, 2005.

[ 7 ] Priestley M J N, Seible F, Calvi G M. Seismic Design and Retrofit of Bridges [M]. New York: Wiley-Interscience, 1996.

[ 8 ] Fajfar P. A nonlinear analysis method for performance based seismic design [J]. Earthquake Spectra, 2000,16(3): 573-592.

[ 9 ] ATC prestandard and commentary for the seismic rehabilitation of buildings [R]. Report No. FEMA-365, Federal Emergency Management Agency, Washington, DC, 2000.

[10] Chopra A K, Geol R K, Chintanapakdee C. Evaluation of a modified MPA procedure assuming higher modes as elastic to estimate seismic demands [J]. Earthquake Spectra, 2004,20(3): 757-778.

[11] Casarroti C, Pinho R. An adaptive capacity spectrum method for assessment of bridges subjected to earthquake action [J]. Bulletin of Earthquake Engineering, 2007,5(3): 377-390.

[12] Priestley M J N, Calvi G M, Kowalsky M J. Displacement-based seismic design of structures [M]. Pavia: IUSS Press, 2007.

[13] ATC prestandard and commentary for the seismic rehabilitation of buildings [R]. Report No. FEMA-440, Federal Emergency Management Agency, Washington, DC, 2005.