行波效应对大跨多塔悬索桥纵向约束体系影响研究

闫聚考 李建中 彭天波

(同济大学土木工程防灾国家重点实验室,上海 200092)

1 引 言

多塔悬索桥为多支承结构，具有超长的跨度，当地震动经过这样长距离的传播时，不同支承点在同一时刻遭受的地震激励很不相同，地震动空间变化的影响不容忽视。

国内外学者对大跨悬索桥在行波效应下的地震反应进行了一些的研究。早在1965年Bogdanoff[1]等建立了简化的悬索桥计算模型，对其进行了行波效应分析。Dumanoglu[2-4]等对欧洲三座大跨悬索桥(Humber, Bogazici, Fatih)建立了三维有限元模型，用不同剪切波速，纵向、横向输入下进行了地震反应分析。Abdel-Ghaffa[5-6]等利用实际的地震记录，在时域和频域内对金门大桥进行了竖向和横向输入下的地震反应分析。魏凯等[7]利用绝对位移法计算了多联长跨组合结构桥梁在多种行波激励模型下的地震响应。胡世德等[8]利用自编程序对江阴长江公路大桥进行了考虑行波效应的地震反应分析。这些研究结果表明，一致激励并不能代表最不利的地震输入，在对大跨悬索桥进行地震反应分析时不能忽略行波效应的影响。

以上文献的研究多是对传统两塔悬索桥进行的，邓育林[9]对大跨三塔悬索桥进行了分析，但采用的是线性时程分析，不能够反映结构的非线性。本文以泰州长江公路大桥为背景，用非线性时程方法，分析了行波效应对大跨三塔两跨悬索桥不同纵向约束体系的影响。

2 基本理论与模型

2.1 多点激励分析理论

考虑随时间和空间变化的地震动多点激励时，大跨桥梁结构的地震反应分析方法可以分为两大类：一类是以地震地面运动为确定过程的确定性分析方法，主要包括反应谱法和时程分析方法；一类是以地震地面运动为随机过程的概率性分析方法，主要是指随机振动法。目前大跨桥梁考虑多点激励和行波效应仍多采用确定性的方法。绝对位移法是一种同时考虑多点激励和非线性地震反应的分析方法。对于图1所示的多自由度体系，按结构节点s、基础节点f及结构与基础界面的公共节点c分块,假设Us为结构位移，Uc为公共节点处位移，Uf为基础位移。

图1 结构和基础组合模型Fig.1 Structure and foundation of model

按结构分析中有限元方法的直接刚度法原理，以绝对位移U的形式建立土-结构整个系统的动力平衡方程[10]：

(1)

其中在接触节点的质量和刚度是结构(s)与基础(f)贡献之和，即有下两式：

(2)

U可以表示为式(3):

(3)

其中，uc为结构运动引起的公共节点位移；uf为结构运动引起的基础位移；vc为自由场运动引起的公共节点位移；vf为自由场运动引起的基础位移。

基础自由场运动要求：

(4)

把式(3)代入方程式(1)，考虑式(4)自由场响应后, 基础和结构连接采用的是无质量的刚性弹簧，忽略阻尼力。则式(1)可简化为

(5)

式(5)即为多点非一致输入下的结构动力方程，利用式(5)可以求得结构的绝对位移Us。

1.2 有限元计算模型

泰州长江公路大桥主跨为三塔悬索桥，两个主跨的跨度均为1 080 m，主缆的分跨为(390+1 080+1 080+390) m。其中，中塔为变截面钢塔，塔高194 m，横桥向为门式框架结构，纵向人字形。叉开处设等截面梯形钢横梁，梁高5 m，上横梁采用横桥向倒K形横梁。边塔包括上塔柱、下塔柱和上下横梁、下横梁，塔柱采用箱形断面，采用C50混凝土。塔柱顶高程180 m。加劲梁采用抗风性能好、整体性强、造型美观的封闭式流线型扁平钢箱梁，加劲梁设上斜腹板及下斜腹板构成导风嘴。中塔下横梁上不设竖向支座，也不设0号吊索，在塔内侧壁与主梁间安装横向抗风支座，限制主梁的横向位移，纵向设弹性索。在边塔处设置竖向和侧向支座。

图2 泰州长江公路大桥立面布置图(单位：m)Fig.2 Elevation of Taizhou Changjiang Highway Bridge (Unit: m)

三维有限元模型如图3所示。利用空间梁单元模拟主梁、主塔和墩柱，用空间杆单元模拟主缆、吊杆；主缆、主塔和吊杆均考虑恒载引起的几何刚度的影响。中塔和主梁之间在纵向采用弹性索连接，弹性刚度取为6.4×105kN/m。对于边塔，由于一般冲刷层位尚在承台底面以上，属于低桩承台基础，采用在承台底中心加6×6的土弹簧来模拟桩土相互作用，而对于中塔，不考虑沉井-土相互作用，在一般冲刷线处将沉井固结。

图3 有限元模型Fig.3 Sketch of FEM model

为比较不同塔梁间纵向约束形式下，行波效应对三塔两跨悬索桥地震响应的影响，本文考虑了5种计算模型，如表1所示。

表1纵向约束体系

Table1Longitudinalconstraintsystems

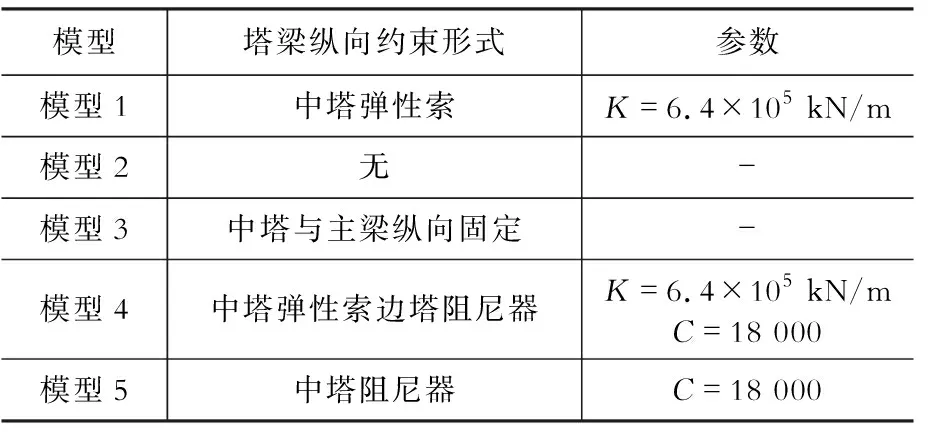
模型塔梁纵向约束形式参数模型1中塔弹性索K=6.4×105 kN/m模型2无-模型3中塔与主梁纵向固定-模型4中塔弹性索边塔阻尼器K=6.4×105 kN/mC=18 000模型5中塔阻尼器C=18 000

2 地震动输入

地震动输入采用《泰州长江大桥地震安全评价报告》超越概率100年3%的人工合成7条加速度时程曲线。其中,位移时程是通过对加速度时程的两次积分得到的,并对积分结果进行了基线修正以消除零位漂移误差的影响。典型地震动输入如图4所示。

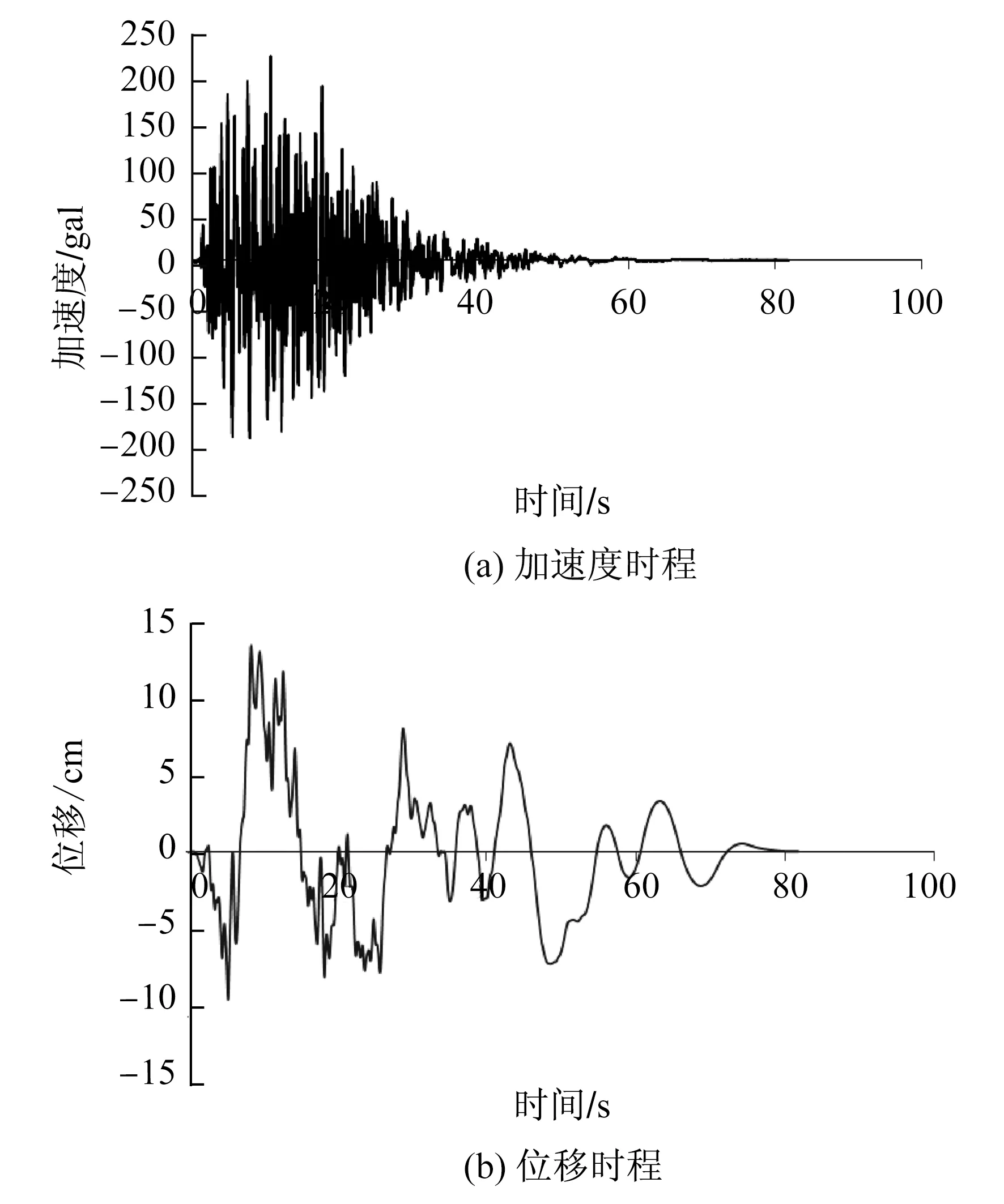
图4 地震动输入Fig.4 Ground motion input

地震波行进波速选取为125 m/s,150 m/s,200 m/s,300 m/s,400 m/s,500 m/s,1 000 m/s,1 500 m/s,2 000 m/s，波速无限大即一致激励情况等10种行进波速进行了分析。由于结构对称性较好，仅考虑地震波从南端向北端传播。计算结果取7条地震波的平均值。

3 地震反应分析

针对上述模型采用非线性时程的方法, 输入泰州人工波进行计算分析。以桥塔塔底作为地震受力分析的关键位置, 以塔梁相对位移及主梁与引桥梁相对位移塔为结构位移分析对象,考察行波效应对不同约束体系多塔悬索桥地震反应的影响。

3.1 关键位置内力分析

图5—图7分别给出了地震波视波速变化对中塔塔底、北塔塔底和南塔塔底内力的影响。图5—图7中纵坐标为考虑行波效应与不考虑行波效应地震响应的比值。

从图5(a)、图5(b)可以看出，对于中塔，5种模型下行波效应都会减小其地震反应。模型1,2,5三种体系随视波速变化，有相似的规律。视波速125～200 m/s变化时，地震反应随波速增加而增大；视波速200～400 m/s变化时，地震反应随波速增加而减小；视波速400～2 000 m/s变化时，地震反应随波速增加而增加，其中视波速为500 m/s时，出现峰值。模型3中塔底剪力，随视波速变化不是很大，在0.49～0.75之间，视波速为400 m/s时，这个剪力比值为0.49，视波速为1 000 m/s时，这个剪力比值为0.75。弯矩和剪力有相似的变化规律。模型4塔底剪力，随视波速变化不是很大，在0.51～0.72之间，视波速为1 000 m/s时，这个剪力比值为0.51，视波速为500 m/s时，这个剪力比值为0.72。弯矩和剪力有相似的变化规律。

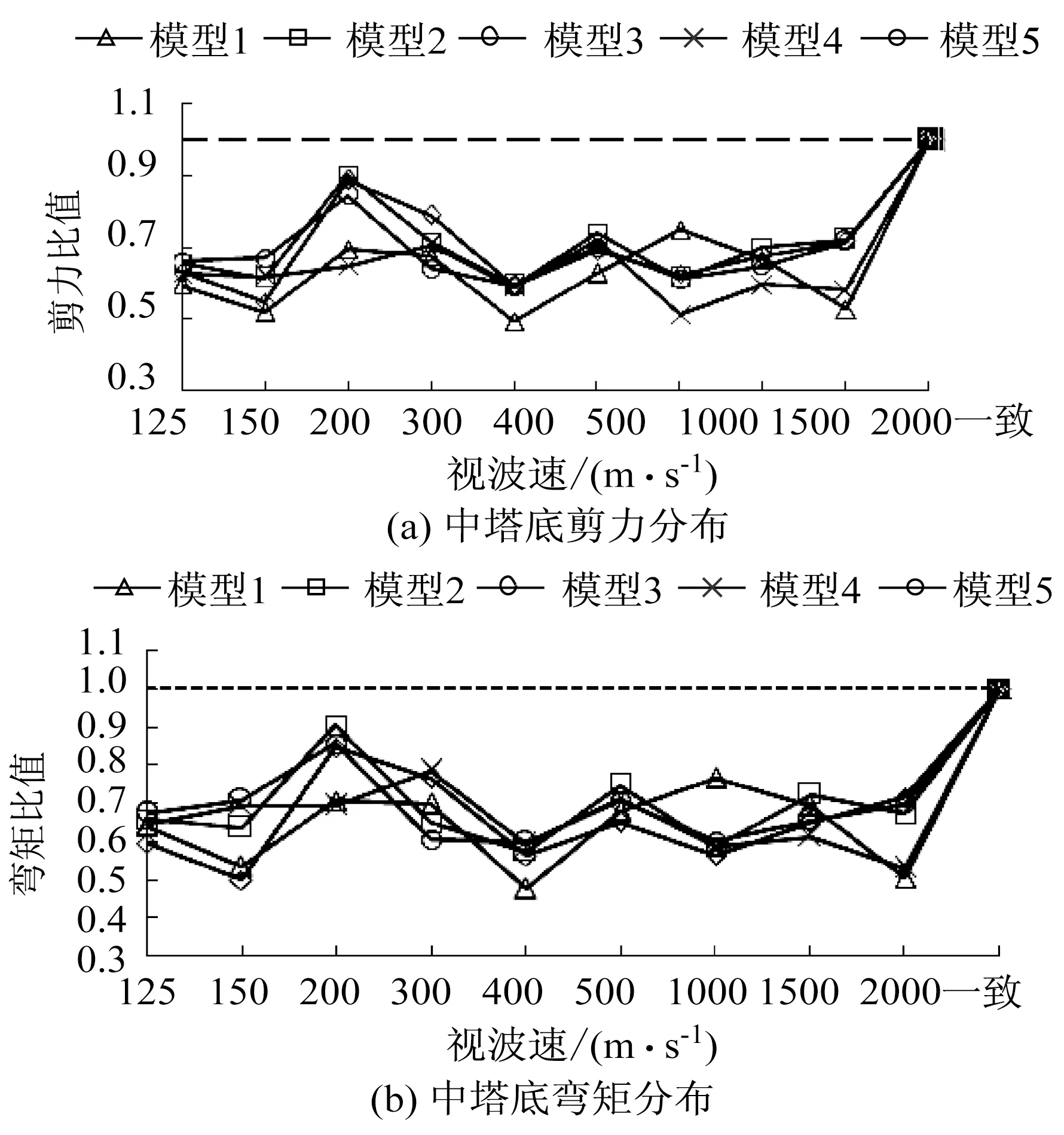
图5 中塔底内力与视波速关系图Fig.5 Force-velocity relation in middle tower

从图6(a)、图6(b)可以看出，在考虑行波效应时，5个计算模型北边塔的内力随视波速变化，有相似的规律。视波速125～200 m/s变化时，地震反应随波速增加而增大；视波速200～400 m/s变化时，地震反应随波速增加而减小；视波速400～2 000 m/s变化时，地震反应随波速增加而增加。模型1,2,5在视波速为2 000 m/s时，行波效应增大北边塔底截面的剪力，模型3,4在行波效应下减小北边塔底截面的剪力。模型1,2,3,5在视波速为200 m/s时，行波效应增大边塔底截面的弯矩。模型4在视波速为125 m/s，1 000 m/s时，行波效应增大边塔底截面的弯矩，最大增幅为11.2%。

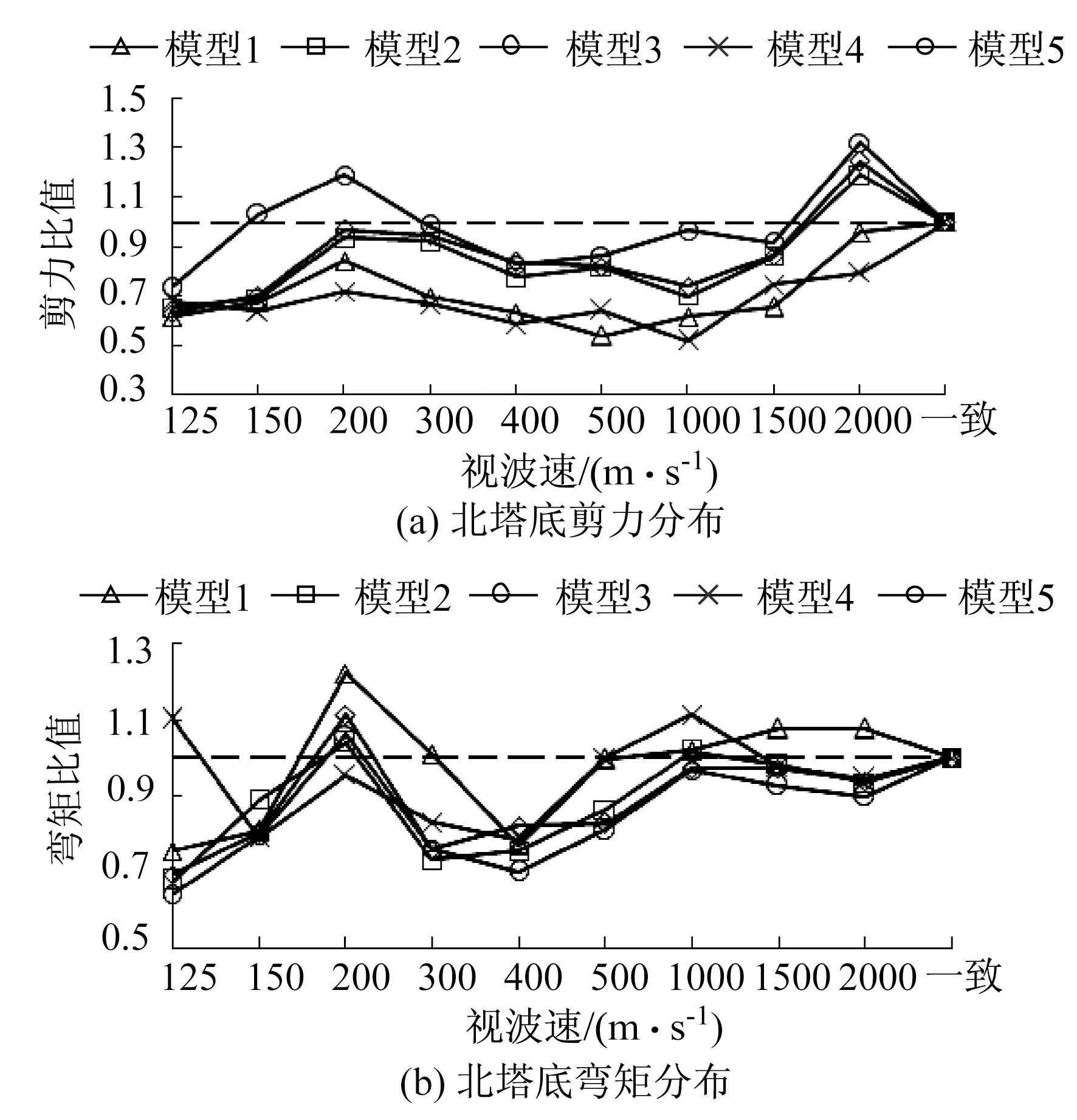
图6 北塔底内力与视波速关系图Fig.6 Force-velocity relation in north tower

从图7(a)、图7(b)可以看出，对于南边塔，模型1,2,4,5行波效应下都会减小结构的地震反应。模型3在视波速为300 m/s时，行波效应增大南塔底截面弯矩30%。行波作用会减小5个模型南塔底截面的剪力。行波效应对模型2的影响最大，模型1、模型5、模型3次之，对模型4的影响最小。

图7 南塔底内力与视波速关系图Fig.7 Force-velocity relation in south tower

3.2 相对位移分析

图8—图12分别给出了地震波视波速变化对边塔、中塔处塔梁相对位移，主梁与引桥梁相对位移的影响。图中纵坐标为考虑行波效应与不考虑行波效应的位移比值。

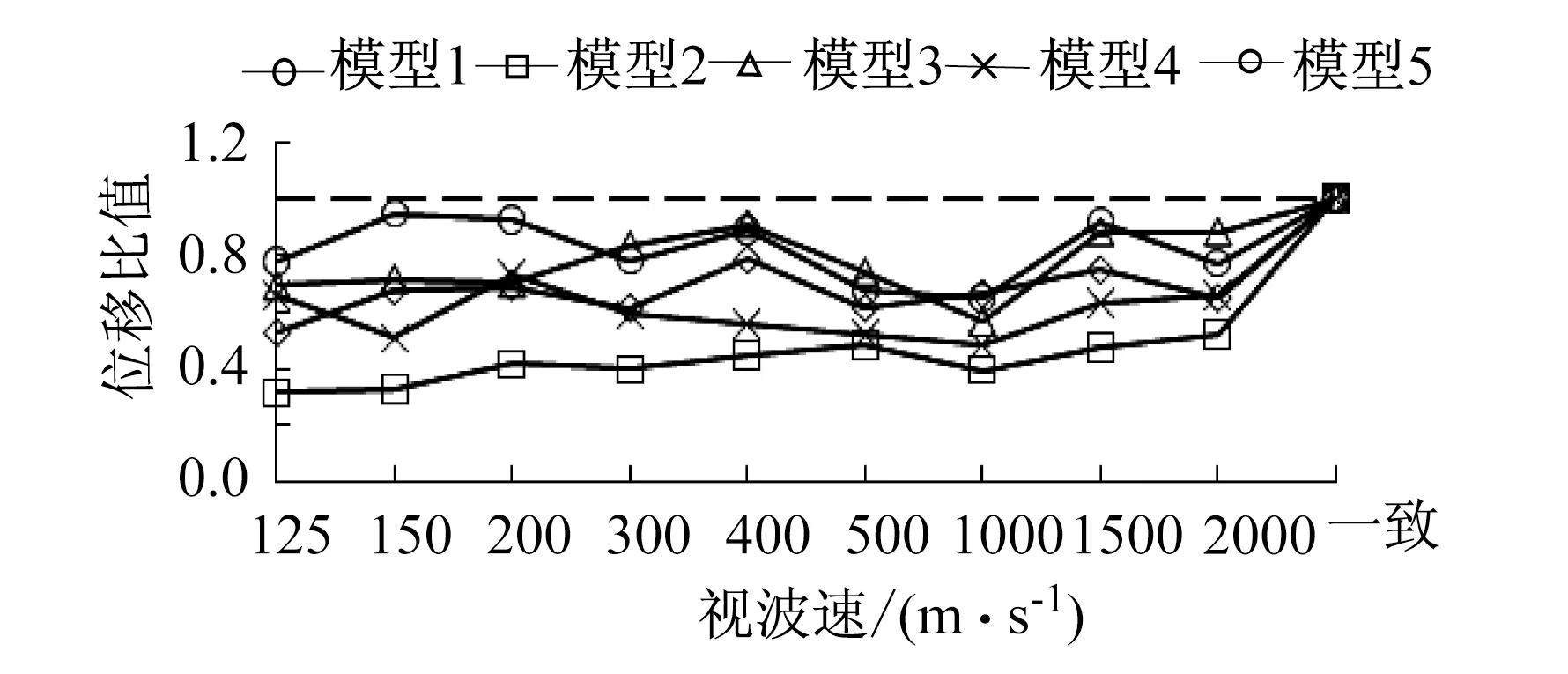
图8 北塔塔-梁相对位移Fig.8 The relative displacement of north tower-beam

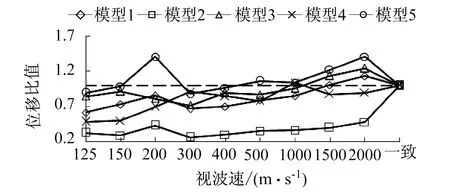
图9 南塔塔-梁相对位移Fig.9 The relative displacement of south tower-beam

从图8—图12可以看出，考虑行波效应时5个模型的北塔塔梁相对位移会减小，其中模型2减小最多。视波速为1 500 m/s,2 000 m/s时，行波效应会增大模型1,3,5的南塔塔梁相对位移，最大增幅达40.8%。对于中塔塔梁相对位移而言，行波效应会增大模型4,5的反应，视波速为1 000 m/s时，模型5增幅为31.5%。考虑行波效应时，5个模型主梁北端与引桥梁的相对位移都会减小，模型2减小最多。考虑行波效应时，模型3,5的主梁南端与引桥梁的相对位移会增大，模型5的最大增幅为11.7%。

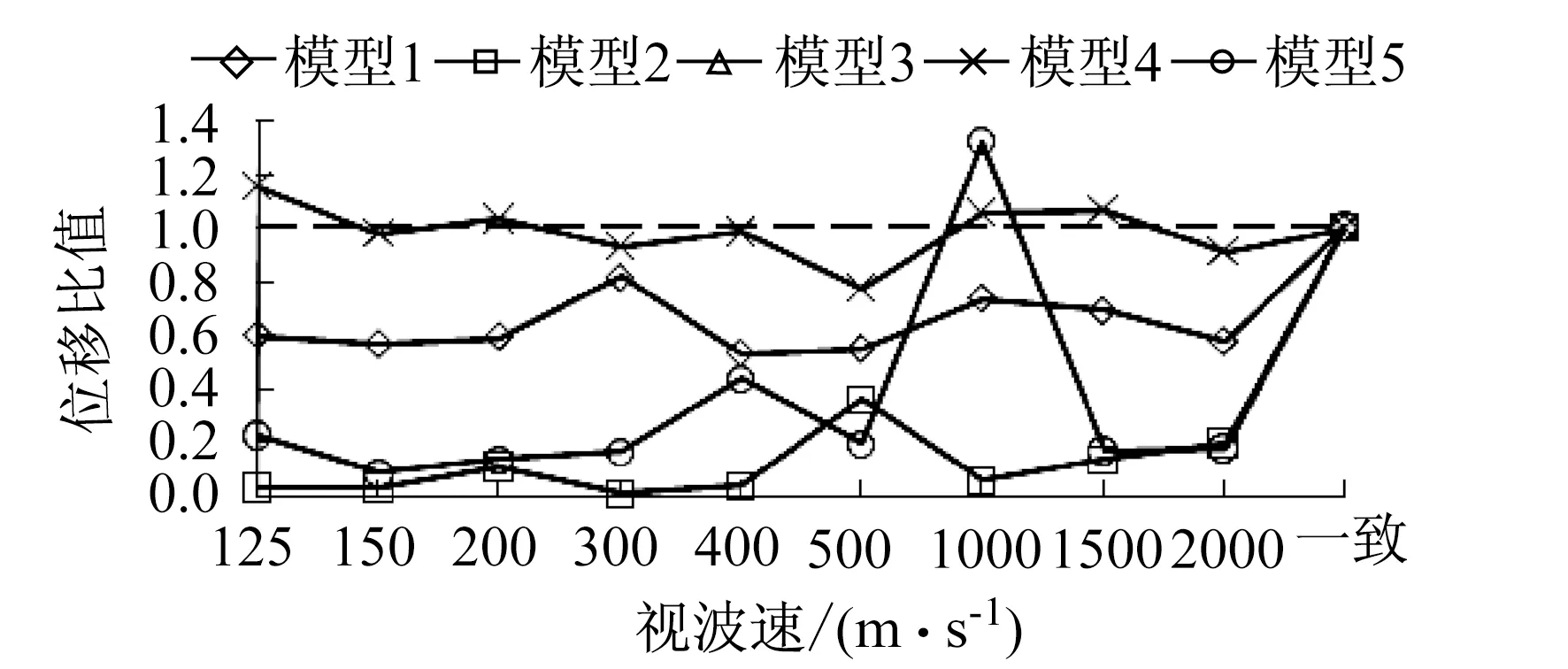
图10 中塔塔-梁相对位移Fig.10 The relative displacement of middle tower-beam

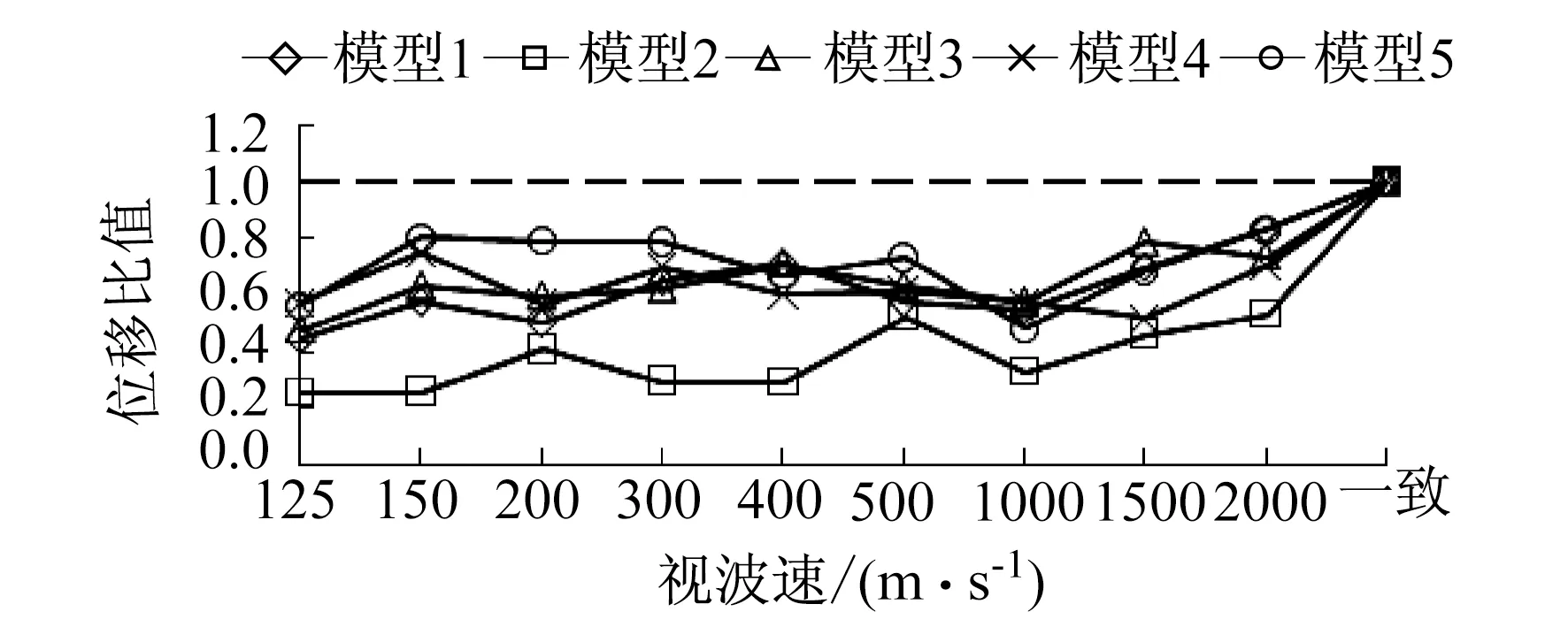
图11 北端梁与引桥梁相对位移Fig.11 The relative displacement between north main beam and approach beam

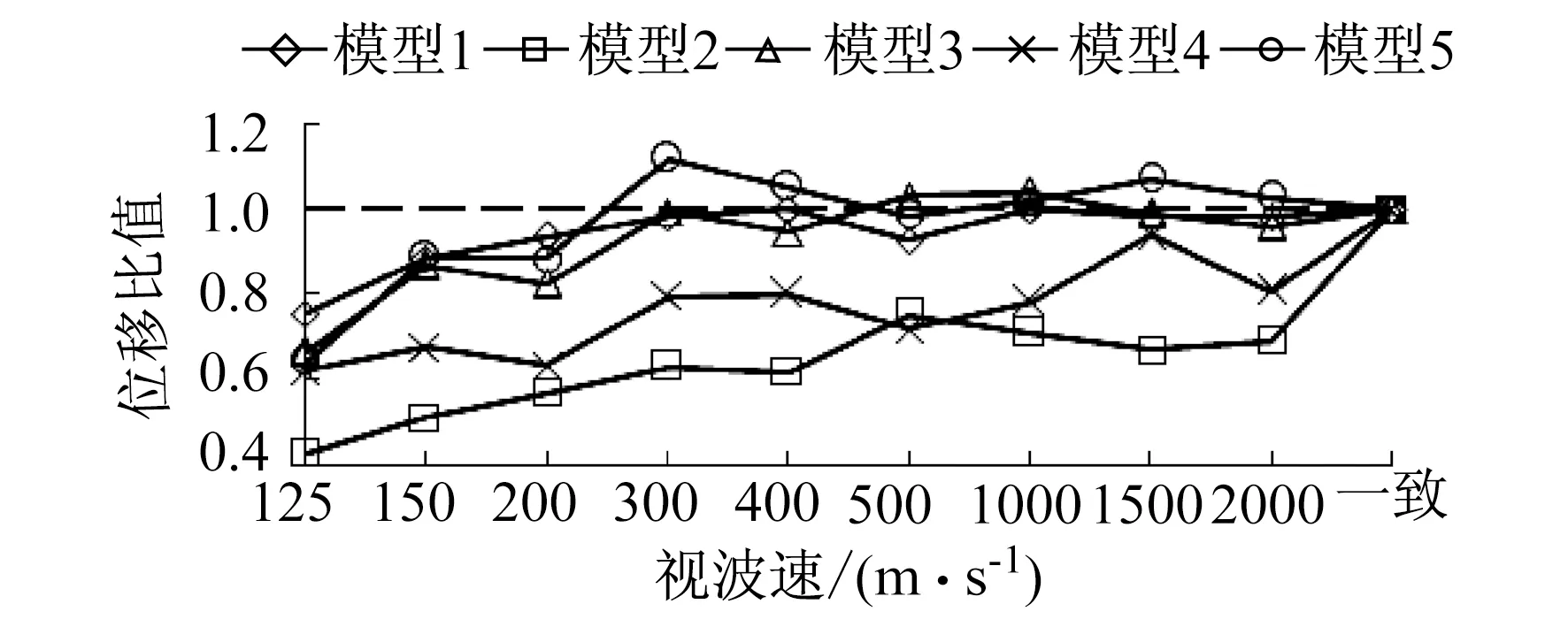
图12 南端梁与引桥梁相对位移Fig.12 The relative displacement between south main beam and approach beam

4 结 论

本文以泰州桥为研究对象，分析多种行波模型下该结构的地震响应，分析结果表明：

(1) 对于5种不同的塔梁纵向约束体系，行波效应均会不同程度地减小中塔的内力。对于北边塔，在考虑行波效应时，5个模型随视波速变化，有相似的规律。模型1，2，5在视波速为2 000 m/s时，行波效应增大北边塔底截面的剪力；模型1,2,3,5在视波速为200 m/s时，行波效应增大边塔底截面的弯矩。对于南边塔，在考虑行波效应时，行波效应均会减小5个模型南塔底截面的剪力；模型3在视波速为300 m/s时，行波效应增大南塔底截面弯矩30%。

(2) 行波效应会增大南塔、中塔处的塔梁相对位移，其中阻尼器体系时，最大增幅达31.5%。因此，在设计阻尼器行程时应当考虑行波效应的影响。考虑行波效应时，模型3,5的主梁南端与引桥梁的相对位移会增大，模型5的最大增幅为11.7%。因此，在进行伸缩缝长度设置时应当考虑行波效应的影响。

[ 1 ] Bogdanoff J L, Goldberg J E, Schiff A J. The effect of ground transmission time on the response of long structures[J]. Bulletin of the Seismological Society of America, 1965,55(3): 627-640.

[ 2 ] Dumanoglu A A, Severn R T. Seismic response of modern suspension bridges to asynchronous vertical ground motion[J]. Institution of Civil Engineers, Proceedings: 1987, 83: 701-730.

[ 3 ] Dumanoglu A A, Severn R T. Seismic response of modern suspension bridges to asynchronous longitudinal and lateral ground motion[J]. Institution of Civil Engineers, Proceedings: 1989, 87: 73-86.

[ 4 ] Dumanoglu A A, Brownjohn J M W, Severn R T. Seismic analysis of the fatih sultan mehmet (second Bosporus) suspension bridge[J]. Earthquake Engineering and Structural Dynamics 1992,21(10): 881-906.

[ 5 ] Abdel-Ghaffar A M, Stringfellow R G. Response of suspension bridges to travelling earthquake excitations: Part I. vertical response [J]. International Journal of Soil Dynamics and Earthquake Engineering 1984,3(3): 62-72.

[ 6 ] Abdel-Ghaffar A M, Stringfellow R G. Response of suspension bridges to travelling earthquake excitations: Part Ⅱ. lateral response [J]. International Journal of Soil Dynamics and Earthquake Engineering 1984,3(3): 73-81.

[ 7 ] 魏凯,郭平,韩萍,等.行波效应下多联长跨组合结构桥梁地震响应分析[J].结构工程师,2010,26(2)：119-125.

Wei Kai, Guo Ping, Han Ping, et al. Seismic responses of a long multi-span composite bridge under traveling wave excitation [J]. Structural Engineers, 2010,26(2)：119-125. (in Chinese)

[ 8 ] 胡世德,范立础.江阴长江公路大桥纵向地震反应分析[J].同济大学学报,1994,22(4):433-438.

Hu Shide, Fan Lichu. The longitudinal earthquake response analysis for the Jiangyin Yangtze river bridge [J]. Journal of Tongji University,1994,22(4):433-438. (in Chinese)

[ 9 ] 邓育林,何雄军.行波效应对大跨多塔悬索桥地震反应的影响分析[J].武汉理工大学学报,2011,35(3):443-447.

Deng Yulin, He Xiongjun. Effect of seismic wave passage on seismic response of long-span multi-tower suspension bridges[J].Journal of Wuhan University of Technology, 2011,35(3):443-447. (in Chinese)

[10] Wilson E L. Three dimensional static and dynamic analysis of structures: a physical approach with emphasis on earthquake engineering[M]. Computers and Structures Inc., 1998.