轮式预应力钢结构施工模拟方法研究

罗永峰 白 洁 贾宝荣 陈晓明

(1. 同济大学建筑工程系，上海 20092； 2. 上海机械施工集团有限公司，上海)

1 引 言

对于传统的钢结构施工方法，采用分阶段独立建模法、状态叠加法或生死单元法进行施工过程模拟分析就能得到较为准确的计算结果，其中分阶段独立建模法与状态迭加法适用于非线性效应不明显的结构，而生死单元法适用于非线性效应明显的结构[1-3]。然而，随着施工技术的进步，近年来出现一些创新的施工方法，如攀达穹顶法、折叠展开法、提升扩展法以及摩天轮的竖立旋转法等[4,5]，这些施工方法的共同特点是在安装构件的同时结构还产生大的刚体位移(可称为“既生长又运动”的结构施工过程)。而现有施工模拟计算方法只能模拟单纯增加构件而结构无刚体大位移的施工过程，无法将结构发生刚体位移前后的施工步关联起来进行分析，也就无法考虑结构刚体位移前已产生的变形与应力对刚体位移后结构刚度矩阵的非线性影响，因而，难以得到准确的施工过程模拟计算结果。

竖立旋转安装法是用于摩天轮结构的一种创新施工方法，是一种在竖直平面内通过旋转完成摩天轮拼装的施工方法，其主要施工技术包括：首先将轮缘分成均等的几瓣，在连接转动中心与轮缘的刚性轮辐辅助下安装第一瓣轮缘，之后将安装好的轮缘绕转动中心向一侧旋转一定角度，接下来安装下一瓣轮缘，然后将安装好的两瓣轮缘再向同侧旋转相同角度，再安装后续轮缘，以此类推，完成整个摩天轮的安装。施工过程如图 1所示。

由于竖立旋转安装法具有结构同时产生刚体位移与变形的特点，现有的钢结构施工过程模拟计算方法难以适用，为此，本文以北京摩天轮结构施工模拟分析为背景，研究竖立旋转安装法的精确数值模拟计算技术，推导结构旋转后的位移向量、荷载向量和切线刚度矩阵的扩展与修正方法，提出结构有刚体大转角位移的施工过程模拟计算方法，为该工程施工模拟提供理论依据和计算方法，为类似钢结构施工提供参考资料与技术方法。

2 实现刚体旋转的施工力学基本原理

根据非线性有限元基本原理，求解施工力学问题实质就是求解以下方程组：

[K]{u}={F}

(1)

式中，[K]为结构刚度矩阵；{u}为位移向量；{F}为荷载向量。

假设在第n+1施工步时，结构在前面的n步已有施工变形且绕O′点产生刚体转角位移θ(图1)，则旋转后结构的刚度矩阵、节点坐标以及荷载列阵都会发生变化，此时结构平衡方程为

[KR]{uR}={FR}

式中，[KR]为结构旋转后的刚度矩阵；{uR}为位结构旋转后的位移向量；{FR}为结构旋转后的荷载向量。

结构旋转后平衡方程中的各项，需要通过其变化量推导确定。

2.1 旋转前后结构刚度矩阵的变化

根据矩阵位移法基本原理，结构的整体刚度矩阵是由整体坐标系下的单元刚度矩阵按照“对号入座”的方法组合形成的，而整体坐标系下的单元刚度矩阵是由局部坐标系下的单元刚度矩阵经坐标转换形成的。由结构力学可知，刚架单元的坐标转换矩阵形式为[6]

(2)

(3)

结构旋转后，各单元在其局部坐标系下的单元刚度矩阵不变，而其局部坐标系相对于整体坐标系的方向发生了变化。如图 2所示，设结构中构件AB绕O′点发生逆时针刚体转角位移θ，构件AB在旋转前与整体坐标系的夹角为α。将构件AB与O′平移，令O′与整体坐标系原点O重合。则构件AB绕O′逆时针旋转θ度相当于整体坐标系xoy绕原点O顺时针旋转θ度到x′oy′，则此时构件AB相对于整体坐标系的夹角为β=α+θ。

结构旋转后，构件相对于整体坐标系的夹角由α变为β=α+θ。因此，构件刚度矩阵的旋转可以通过改变坐标转换矩阵T中局部坐标系与整体坐标系的夹角实现，则此时刚架单元的坐标转换矩阵变为

图2 构件旋转后与整体坐标系夹角示意图Fig.2 Angle between member and global coordinates system after rotation

(4)

(5)

2.2 旋转前后荷载列阵的变化

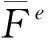
(6)

2.3 旋转前后结构节点坐标的变化

在第n+1施工步发生刚体旋转位移后，后续施工步产生的变形都是相对于结构旋转后位形的变形。设结构初始节点坐标为{C0}，前n个施工步产生的累积位移为{un}，则n个施工步后的节点坐标为{Cn}={C0}+{un}。在第n+1施工步，结构旋转后的节点坐标{CnR}需采用旋转变换的方法推导。

如图 3所示，A点为结构中任意一点，设A绕O′点产生顺时针转角θ到达A′点，由图可知有如下向量关系：

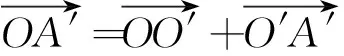
(7)

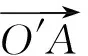
(8)

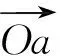
(9)

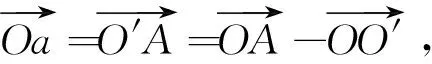
(10)

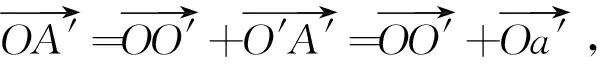
(11)

按上述方法计算结构旋转后所有节点坐标，组装起来即可得到旋转后的节点坐标列向量{CnR}。

综上所述，可以通过转换刚度矩阵与荷载列阵得到旋转后的结构刚度方程[KR]{uR}={FR}，但必须注意，求解此方程得到的位移是相对于旋转后的结构位形{CnR}的。

3 采用ANSYS实现施工中刚体旋转的基本原理

3.1 复原构件变形与应力的方法

ANSYS中的命令UPGEOM可将以前分析得到的位移累加到有限元模型上，并生成一个已变形的几何模型，缺省时该命令作用在所有节点上，也可以选择一组节点。若重复执行该命令，则位移结果将累加，以改变节点坐标并生成新的有限元模型[7,8]。

ISWRITE命令可将计算得到的构件应力保存在文件中。ISFILE命令通过从应力文件中读取应力数据给单元施加初应力。初应力荷载只能在第一个荷载步施加，且只能在求解层施加。初应力荷载的施加采用覆盖的方式，即多次施加时后面的命令覆盖前面命令的结果。

利用上述几种命令，即可在新建模型中复原原模型的变形与应力，具体方法如下：

第一步，建立完整的结构有限元模型，施加边界约束条件与荷载并进行求解，执行ISWRITE命令生成初应力文件(.IST文件)与变形文件(RST文件)。

第二步，按照设计位形建立与上一步相同的有限元模型，执行UPGEOM命令导入上一步计算得到的变形文件(.RST文件)以更新有限元模型。

第三步，施加边界条件及荷载，执行 ISFILE 命令从第一步计算生成的初应力文件(.IST文件)施加初应力荷载，进行计算。第三步计算得到的位移是在UPGEOM更新位形上产生的位移。

3.2 刚体旋转后复原旋转前构件变形与应力的方法

采用ANSYS计算得到的单元数据结果(如应力和应变)按照单元局部坐标系的方向保存在结果文件中，因此，无论构件位置发生什么变化，只要单元编号不变，单元坐标系从I节点到J节点的指向不变，则通过ISFILE命令输入的单元坐标系下的初始应力荷载就不变。节点的计算结果(如位移)按照节点坐标系的方向保存在计算结果文件中。由于ANSYS缺省的节点坐标系方向平行于整体坐标系，则当构件发生旋转后，单元坐标系的方向随构件方向而转动，但节点坐标系方向仍然与整体坐标系相同，导致节点坐标系与单元坐标系的相对方向发生变化。要保持单元坐标系与节点坐标系的相对方向不变，就需要对旋转后构件的节点坐标系进行旋转变换，使单元坐标系与节点坐标系的相对方向保持不变。在节点坐标系旋转之后，再使用UPGEOM命令导入旋转前计算得到的节点位移，则得到的构件旋转后的位形与旋转前的位形在单元坐标系下保持不变。

综上所述，要想在构件发生刚体旋转后复原其旋转前的变形与应力，需要在旋转节点坐标系的基础上使用UPGEOM命令导入节点变位并使用ISFILE命令导入单元初始应力荷载，具体的计算步骤如下：

第一步，建立完整的结构有限元模型，施加边界约束条件与荷载并进行求解，执行ISWRITE命令生成初应力文件(.IST文件)与变形文件(.RST文件)。

第二步，建立旋转后的结构有限元模型，须保证各单元的单元编号、单元两端的节点编号、单元坐标系的I、J节点指向保持不变。

第三步，旋转节点坐标系的方向使其与单元坐标系的相对方向与构件旋转前保持不变。

第四步，执行UPGEOM命令，更新有限元模型，以导入上一步计算结果的变形文件(.RST文件)。

第五步，施加旋转后的边界条件及荷载，执行 ISFILE 命令从上一步计算生成的初应力文件(.IST文件)施加初应力荷载，进行计算。第五步计算得到的位移是在UPGEOM更新位形上发生的位移。

3.3 数值算例验证

一悬臂钢管，截面为φ 50×4.0，悬挑长度为2.5 m，悬臂端作用一竖直向下的集中荷载F=1 kN，不考虑结构自重。坐标原点位于悬臂梁固定端，X轴沿构件方向向右，Z轴竖直向上，计算简图如图 4所示。假设其在变形后绕固定端发生90°逆时针转角，其边界与荷载同时发生旋转，如图5所示。

建立如图 4所示的有限元模型并进行计算，得到弯矩M=2.49 kN·m，悬臂端的竖向位移uz=-163.85 mm。执行ISWRITE命令，生成计算结果文件。

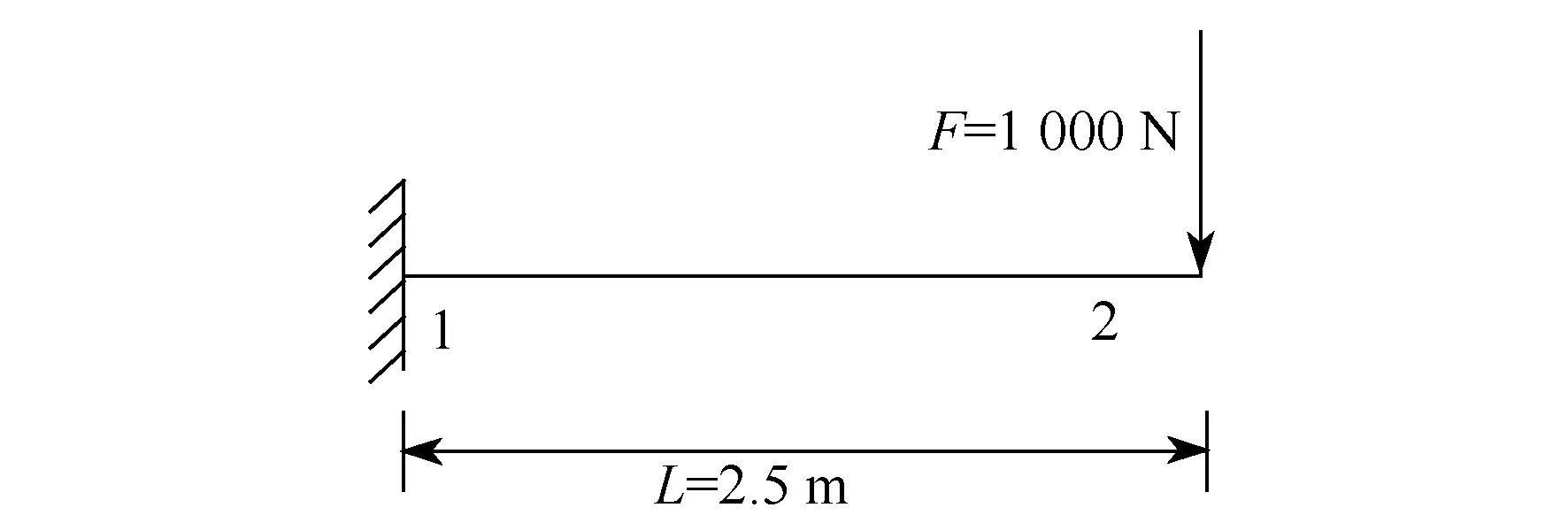
图4 旋转前简图Fig.4 Diagram before rotation

图5 旋转后简图Fig.5 Diagram after rotation

建立如图5所示旋转后的有限元模型，保证单元编号、单元两端节点编号、单元局部坐标系的I、J节点指向保持不变。旋转节点坐标系，将两节点的坐标系逆时针旋转90°，构件旋转后的节点编号和节点坐标系的方向如图 6所示。

图6 节点坐标系旋转后的方向Fig.6 Node coordinates direction after rotation

执行UPGEOM命令，得到更新的有限元模型，且此时悬臂端节点2的坐标为x=163.85 mm，其值与原模型Z方向的变形uz=-163.85 mm相同。

施加旋转后的固定边界条件与悬臂端集中荷载F=1 kN，如图5所示。执行ISFILE 命令导入原模型计算得到的应力，并进行计算，得到旋转后模型固定端弯矩为M=2.49 kN·m，与原模型计算结果M=2.49 kN·m相比误差为0.00%，悬臂端位移为ux=0.228 mm，注意该位移是在原模型已有位移上又产生的位移，故与原模型位移uz=-163.85 mm相比误差为0.14%。

由以上算例可知，本文数值计算方法有效，且误差不超过1%。

4 基于分步建模的坐标旋转法

分步建模法是按照施工步骤依次建立施工阶段的计算模型，且后续施工步的模型是在上次施工步模型已有变形的基础上建立的。不同于分阶段独立建模法，分步建模法可以考虑各个施工步间的互相影响以及变形累积；不同于生死单元法，分步建模法中未安装的单元不会出现在模型中，不存在死单元漂移的影响，消除了未安装单元与已安装单元之间的相互影响。所以，分步建模法可以按照拟定施工方案边建模边求解，可真实、精确地再现整个施工过程，并可精确控制施工过程中的安装位形。因此，若将分步建模法与坐标旋转法结合，就可得到一种可准确模拟带有刚体旋转的“既生长又运动”的施工过程的计算方法，称之为基于分步建模的坐标旋转法，其计算步骤如下：

第一步，建立第一施工步的有限元模型，并加载求解，执行ISWRITE命令。导出第一施工阶段完成时已安装构件的初应力文件(后缀为IST 的文件)和变形文件(后缀为RST 的文件)。

第二步，设此时第一施工步安装的构件发生刚体旋转。建立已安装构件旋转后的有限元模型，保持其节点编号、单元编号、单元I、J节点指向与第一步建立的模型相同，旋转节点坐标系方向使之与单元坐标系的相对方向与旋转前第一步模型中相同。

2.4 不同肥料增效剂对玉米农艺性状的影响 从表3可以看出，各处理穗长在16.70～18.45 cm，各处理间差异不显著，但施肥处理穗长长于不施肥处理，施用增效剂的处理长于常规施肥的穗长，前3位的穗长处理⑨、处理⑩、处理⑥分别比常规处理增加0.87、0.85、0.82 cm。各处理穗粗在4.9～5.2 cm，各处理间差异不显著，但多数施肥处理穗粗长于不施肥处理，前2位的穗粗处理⑨、处理⑩较不施肥处理分别增加0.3、0.3 cm。各处理突尖在0.9～2.0 cm，各处理间差异显著或极显著，但多数施肥处理突尖短于不施肥处理，前2位的突尖处理⑨、处理⑩较不施肥处理分别减少1.1、1.1 cm。

第三步，通过UPGEOM命令导入第一施工阶段完成时已安装构件的变形文件(RST文件)，修正有限元模型。

第四步，在第三步模型的基础上按照新安装构件的定位原则建立第二施工步新增安装单元，形成本阶段完整的有限元模型。

第五步，选择第一施工步安装的构件，执行ISFILE命令导入第一施工步已产生的单元应力荷载。

第六步，选择第一施工步安装的构件，将第一施工步的荷载随结构旋转变换并施加在结构上，进行计算。

第七步，用第二施工步的荷载替代上一步的荷载，进行计算，执行ISWRITE命令。

第八步，若后续施工步还有刚体旋转位移，则重复上述计算过程；若后续施工步不再发生刚体旋转，则继续使用分步建模法完成计算即可。

5 数值算例验证

本节以北京朝天轮的竖立旋转法施工过程为例，验证基于分步建模的坐标旋转法以及与传统分析方法计算结果的差别。北京朝天轮竖立旋转法施工过程如图 1所示，具体步骤为：①先安装刚性轮辐RS1、RS2，然后安装第1个1/8分段轮缘与轮辐索；②牵引轮缘顺时针旋转45°；③安装刚性轮辐RS3，安装第2个1/8分段轮缘与轮辐索；④牵引轮缘顺时针旋转45°；⑤依次进行，直到安装刚性轮辐RS8，安装第8个1/8分段轮缘与轮辐索，轮缘合拢，完成安装。

限于篇幅，本文仅采用1.0自重+1.0预应力的荷载组合进行施工过程模拟计算，其中轮辐索的预应力为3 300 kN。根据文献[9],在轮缘安装阶段，轮辐索应力为设计值的30%。

5.1 采用分阶段独立建模法计算

5.2 采用基于分步建模的坐标旋转法计算

根据实际结构建立有限元模型，采用基于分步建模的坐标旋转法的分析过程示意图如图 7所示，具体分析步骤如下：

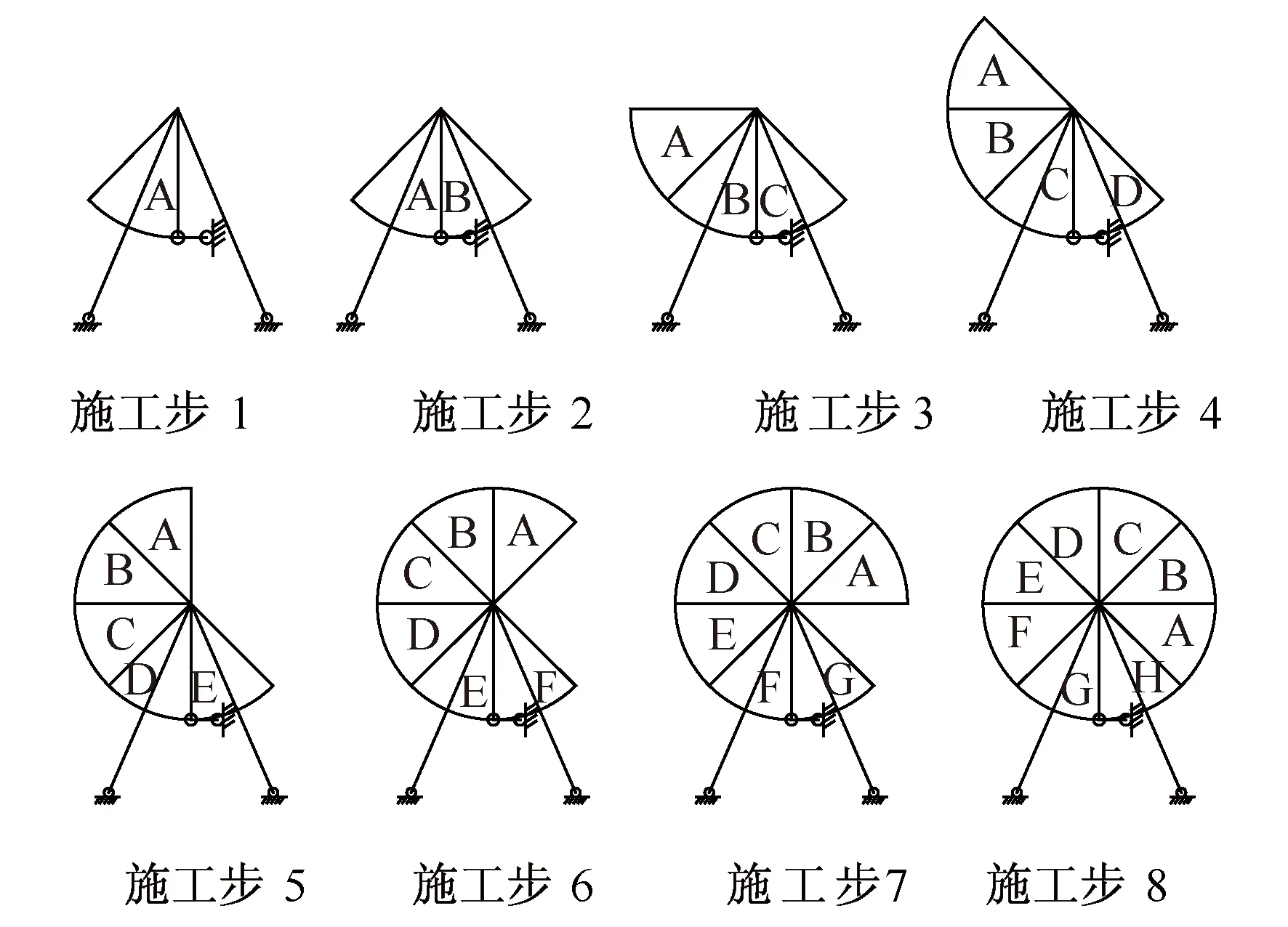
图7 计算过程示意图Fig.7 Calculation process diagram

第一步，建立如图7施工步1所示计算模型，加载预应力与自重进行计算，执行ISWRITE命令，导出第一施工步完成时已安装构件的初应力文件(FILE1.IST)和变形文件(FILE1.RST)。

第二步，建立如图 7施工步2所示模型，其中新增节点的位置按照分步建模法中的设计位形定位准则确定。执行UPGEOM命令导入第一步计算得到的节点位移(FILE1.RST)。执行第一荷载步：选择组件A执行ISFILE命令，导入第一步计算得到的应力荷载(FILE1.IST)，施加第一步的荷载，并进行计算；执行第二荷载步：施加组件B的轮辐索预应力和结构自重进行计算，执行ISWRITE命令得到第二步的位移结果文件(FILE2.RST)与应力文件(FILE2.IST)。

第三步，建立如图 7施工步3所示模型，其中新增节点的位置按照分步建模法中的设计位形定位准则确定。将轮盘单元的节点坐标系顺时针旋转45度，令节点坐标系与单元坐标系的相对方向与第一、二施工步相同，支座仍位于组件A、B之间。执行UPGEOM命令导入第一、第二步计算得到的节点位移(FILE1.RST、FILE2.RST)。执行第一荷载步：选择组件A、B执行ISFILE命令，导入第二步计算得到的应力荷载(FILE2.IST)，施加第二步的荷载，进行计算；执行第二荷载步：施加组件C的轮辐索预应力和自重进行计算，执行ISWRITE命令得到第三步的位移结果文件(FILE3.RST)与应力文件(FILE3.IST)。

第四步，建立如图 7施工步4所示模型，其中新增节点的位置按照分步建模法中的设计位形定位准则确定。将轮盘单元的节点坐标系顺时针旋转90°，令节点坐标系与单元坐标系的相对方向与第一、二、三施工步相同，支座仍位于组件B、C之间。执行UPGEOM命令导入第一、第二、第三步计算得到的节点位移(FILE1.RST、FILE2.RST、FILE3.RST)。执行第一荷载步：选择组件A、B、C执行ISFILE命令，导入第三步计算得到的应力荷载(FILE3.IST)，施加第三步的荷载，进行计算。执行第二荷载步：施加组件D的轮辐索预应力和结构自重进行计算，执行ISWRITE命令得到第四步的位移结果文件(FILE4.RST)与应力文件(FILE4.IST)。

以此类推，分别进行施工步5到施工步8的计算，即可得安装完毕的内力与位移结果。

须注意，由于每一步计算得到的位移均是相对于该步UPGEOM更新节点坐标的，故每一步的实际位移应等于该步UPGEOM后的节点坐标减去UPGEOM前的节点坐标，再加上该步计算得到的节点位移。

5.3 计算结果对比

以安装完毕后刚性轮辐与轮缘的8个公共点(图8)相对于设计位形的位移和安装完毕后48根轮辐索的轴力结果为例，对比分阶段独立建模法和基于分步建模的坐标旋转法的计算结果，刚性轮辐与轮缘的8个公共节点的和位移USUM对比结果如图 9所示，48根轮辐索的轴力对比结果如图 10所示。

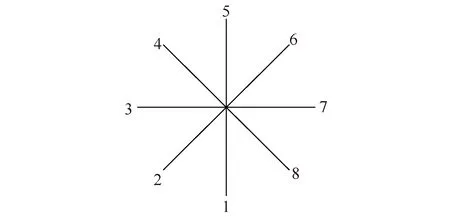
图8 刚性轮辐与轮缘公共点编号图Fig.8 Common nodes of rigid spoke and wheel

对比两种计算方法得到的结果可发现如下规律：

(1) 采用分阶段独立建模法分析认为结构一次成型，由于摩天轮结构受力较为均匀对称，故得到的各节点位移较为均匀，差异不大，且得到的节点位移和坐标旋转法的计算结果相比偏小；

(2) 坐标旋转法与分阶段独立建模法的位移结果在最初完成安装的几个节点处较为接近，而随着施工步的进展，施工变形的累积，后续施工步完成安装的节点的计算结果差异逐渐增大；

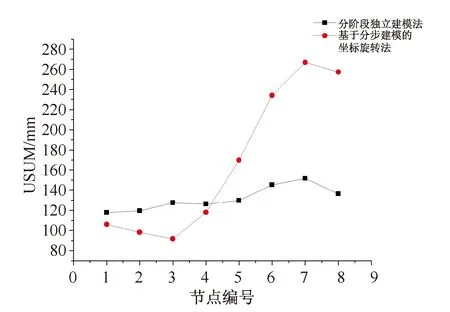
图9 刚性轮辐与轮缘公共节点的和位移USUM计算结果对比Fig.9 Total displacement USUM comparison for the commonodes of rigid spoke and wheel

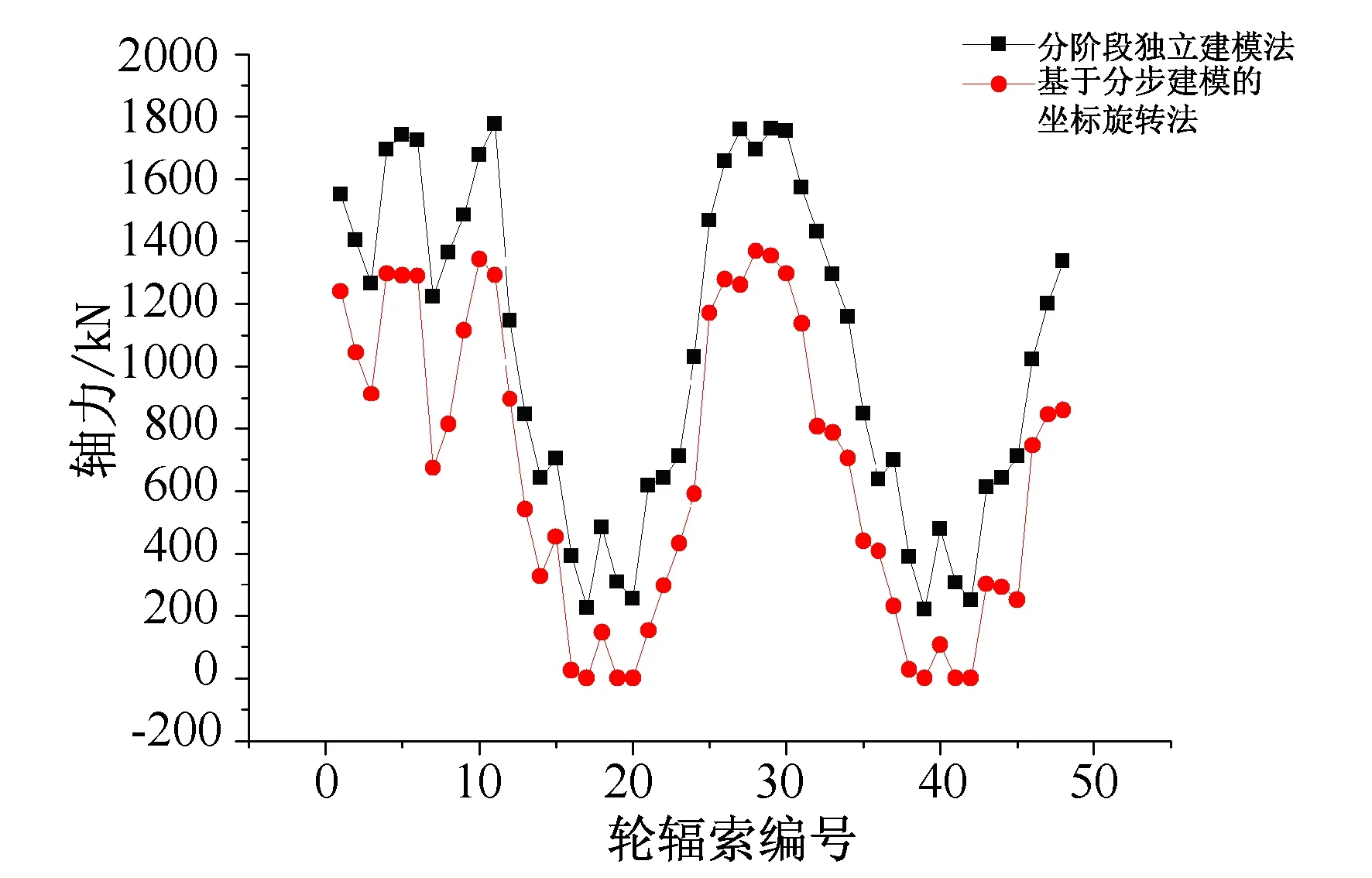
图10 轮辐索轴力计算结果对比Fig.10 Spoke cable tensile force comparison

(4) 采用坐标旋转法与分阶段独立建模法计算得到的所有轮辐索轴力的变化趋势一致；

(5) 采用分阶段独立建模法认为轮辐索索力一次完成张拉，得到的轮辐索索力比坐标旋转法得到的索力偏大；

(6) 坐标旋转法由于可以考虑分批张拉的施工过程中后续张拉对前序已完成张拉的轮辐索轴力的影响，故得到的轮辐索索力比分阶段独立建模法得到的索力偏小。

5 结 论

对于带有刚体旋转位移的施工方法，本文以非线性有限元为理论依据，通过研究刚体大转角位移前后结构位形与刚度矩阵的变化规律，推导出有限元模型在结构旋转后的位移矩阵、荷载矩阵和切线刚度矩阵的扩展与修正方法，为模拟带有大转角位移的施工过程提供了理论依据。

以分步建模法为基础，通过对有限元程序ANSYS计算功能的扩展，提出一种在现有有限元软件基础上实现模拟带有刚体大转角位移的施工过程的便捷有效的施工模拟计算方法——基于分步建模的坐标旋转法，并通过算例验证了其可行性。

通过悬臂梁旋转计算结果说明，本文数值计算方法有效，且误差不超过1%。

通过对北京朝天轮的竖立旋转法施工过程模拟计算比较说明，采用基于分步建模的坐标旋转法对于带有刚体旋转的施工过程有更好的适应性，可以更准确地反映施工过程中以及成型后结构的受力性能。

[ 1 ] 刘学武,郭彦林.考虑几何非线性钢结构施工力学分析方法[J].西安建筑科技大学学报:自然科学版,2008,40(2):161-169.

Liu Xuewu, Guo Yanlin. Construction mechanics analytical procedures for steel structures in view of the geometric nonlinearity[J]. Journal of Xi’an University of Architecture and Technology (Natural Science Edition), 2008,40(2):161-169.(in Chinese)

[ 2 ] 郭彦林,刘学武.钢结构施工力学状态非线性分析方法[J].工程力学,2008,25(10):19-24.

Guo Yanlin, Liu Xuewu, State nonlinear finite element method construction mechanics analysis of steel structures[J]. Engineering Mechanics, 2008,25(10):19-24.(in Chinese)

[ 3 ] 卓新.空间结构施工方法研究与施工全过程力学分析[D].杭州:浙江大学,2001.

Zhuo Xin. Space structures construction methods and whole erection process mechanics analysis for space structures[D]. Hangzhou, Zhejiang University, 2001.(in Chinese)

[ 4 ] 王小盾,余建星,陈志华,等.攀达穹顶技术工法的原理和应用前景[J].建筑技术,2004,35(5):383-384.

Wang Xiaodun, Yu Jianxin, Chen Zhihua, et al. Principle and application prospect of pantadome construction method[J]. Architecture Technology, 2004,35(5):383-384.(in Chinese)

[ 5 ] 罗永峰,王春江,陈晓明.建筑钢结构施工力学原理[M].北京：中国建筑工业出版社,2009.

Luo Yongfeng, Wang Chunjiang, Chen Xiaoming. Construction mechanics principle for building steel strutures[M]. Beijing: China Architecture and Building Press, 2009.(in Chinese)

[ 6 ] 朱慈勉.计算结构力学[M].上海：上海科学技术出版社,1992.

Zhu Cimian, Computational structural mechanics[M]. Shanghai: Shanghai Science and Technology Press, 1992.(in Chinese)

[ 7 ] 王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社,2007.

Wang Xinmin. ANSYS engineering structure numerical analysis[M]. Beijing: China Communications Press, 2007.(in Chinese)

[ 8 ] 郑江.复杂刚性钢结构施工过程力学模拟及计算方法研究[D].西安：西安建筑科技大学,2011.

Zheng Jiang, Research of mechanics simulation and calculating methods during construction process of complex rigid steel structures[D]. Xi’an: Xi’an University of Architecture and Technology, 2011.(in Chinese)

[ 9 ] 白洁.大型摩天轮结构施工模拟方法研究[D].上海:同济大学,2010.

Bai Jie. Researeh of simulation methods during construction process of large scale ferris wheels[D]. Shanghai: Tongji University, 2010.(in Chinese)