明挖基坑近接既有地铁隧道变形计算分析

刘旭政 黄俊斌 张春荣

(1. 华东交通大学土木建筑工程学院，南昌 330013； 2. 西安市政设计研究院有限公司，西安 710068； 3. 江西交通设计研究院有限责任公司，南昌 330002)

1 引 言

随着城市地下轨道交通的不断发展，近年来频繁出现了地下工程的近接施工。近接工程施工时，不可避免地对近邻既有地铁隧道产生附加内力和变形。既有地铁隧道对运营期间的变形要求较高，一旦施工不当，就有可能造成极其严重的后果。因此，近接工程施工时对既有隧道的变形进行准确预测及合理控制，具有十分重要的理论研究和现实意义。

国内外学者对于近接工程展开了较广泛的研究。孙钧等[1]考虑了注浆和盾尾空隙以及盾构推进所产生的地层损失，采用三维弹塑性有限元分析了上海地铁隧道叠交的施工变形问题。陶连金等[2]采用FLAC 3D程序建立了三维地层-结构模型，预测了拟建隧道上穿既有地铁隧道在施工期间的结构变形，并验算了既有结构各部位的承载能力。陈亮等[3]结合现场监测数据及理论分析，分析研究了隧道近距离长穿既有隧道引起的纵向变形过程及其产生原因和机理。刘树佳[4]等针对上海地铁线路的近接工程，采用三维弹塑性有限元模型，分析研究了在不同净距、不同土仓压力、不同注浆量下新建隧道盾构穿越既有隧道管片变形的影响。Yazdchi等[5]提出了在不同地面条件下，用确定的时间步长，估算隧道叠交所引起的地面沉降和对附近结构的影响。

从上述文献可以看出，以往的研究往往集中在采用盾构施工的隧道近接既有隧道产生的一些问题[6，7]，对明挖隧道近接既有地铁隧道研究较少，本文以西安市南门隧道上穿地铁二号线钟楼—南门区间为例，采用有限元程序Midas GTS构建三维弹塑性有限元模型，对比分析了不同工况下基坑底面及地铁管片的变形，并依据研究结果确定了地基加固措施。研究结果可为今后类似工程提供借鉴经验，完善上穿近接工程的施工理论和方法。

2 工程概况

南门隧道与地铁二号线交叉点位于南门城墙以南约84 m处，与地铁二号线左右两线分别交叉，该处地铁二号线左线处于曲率半径R=376 m的圆曲线，右线处于曲率半径R=400 m的圆曲线上。该处地铁二号线为盾构区间段，地铁横断面基本尺寸为区间隧道结构内径为5.4 m，管片厚度为300 mm，隧道外径为6.0 m。南门隧道底板底面距离现状地铁二号线衬砌环顶面最小距离为1.925 m。南门隧道与既有地铁二号线位置示意如图1、图2所示。

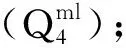
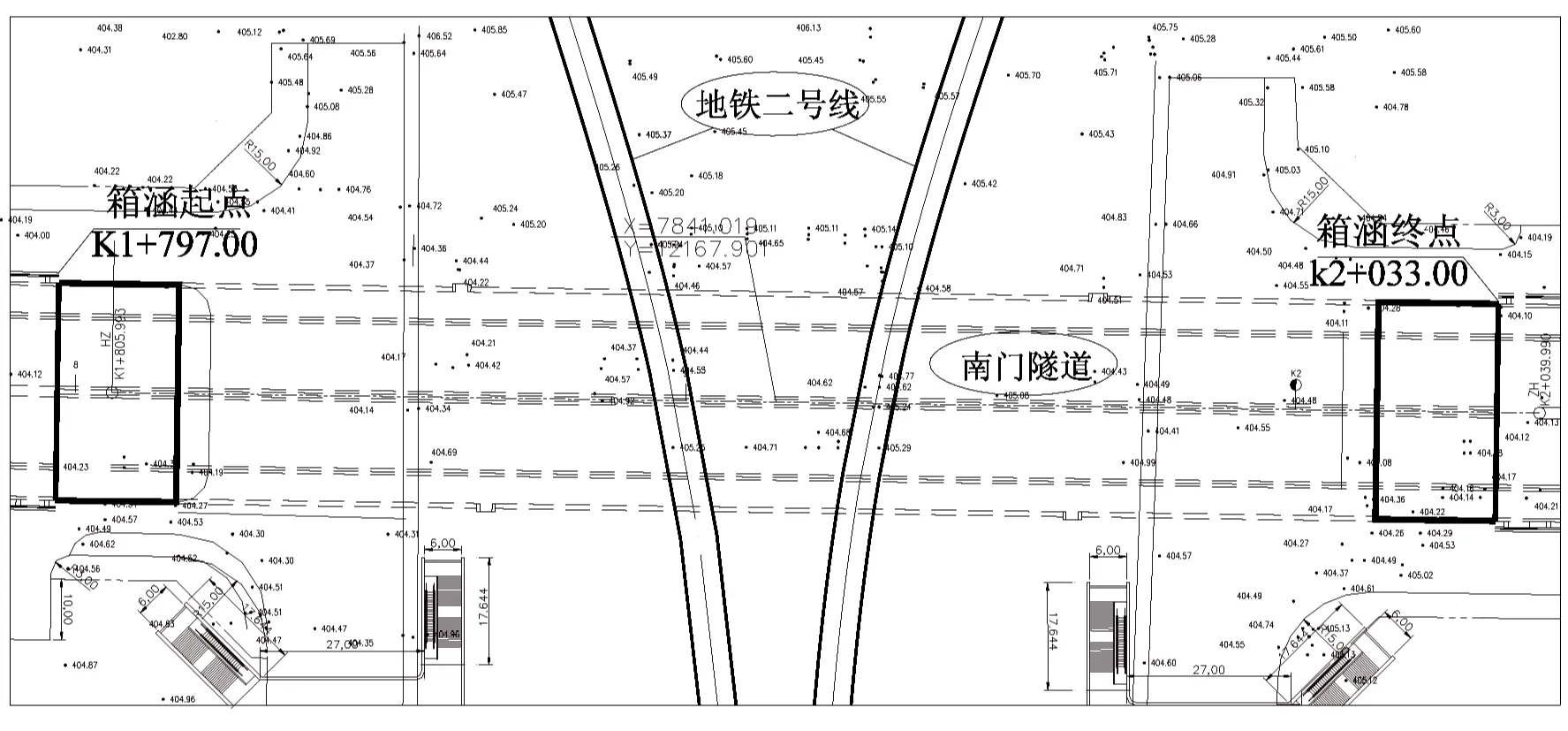
图1 南门隧道与地铁二号线位置平面图Fig.1 Plan at Nanmen tunnel and line No.2

图2 南门隧道与地铁二号线关系示意图 (单位：m)Fig.2 Sketch of the location of Nanmen tunnel and line No.2 (Unit：m)

因周围地形所限，在南门隧道上穿地铁二号线左右线处分别布设基坑，基坑开挖分别施工。一个基坑内隧道节段施工完成，回填完毕后，方可进行另外一个基坑的开挖及隧道节段的施工工作。基坑布置为26 m×39 m×8.3 m(宽×长×深，宽度为东西向，长度为南北向)。南门隧道基坑开挖及支护的整体原则确定为分层、分步、对称、平衡、限时。为保证基坑开挖及地铁上方的南门隧道节段整体施工工期尽可能缩短，将每分块基坑开挖分层数定为4层，每层深度约2 m。平面上的开挖顺序为先周边后中间，抽条均匀开挖。平面开挖顺序见图3。

表1土层物理力学参数

Table1Mechanicalparametersofsoils

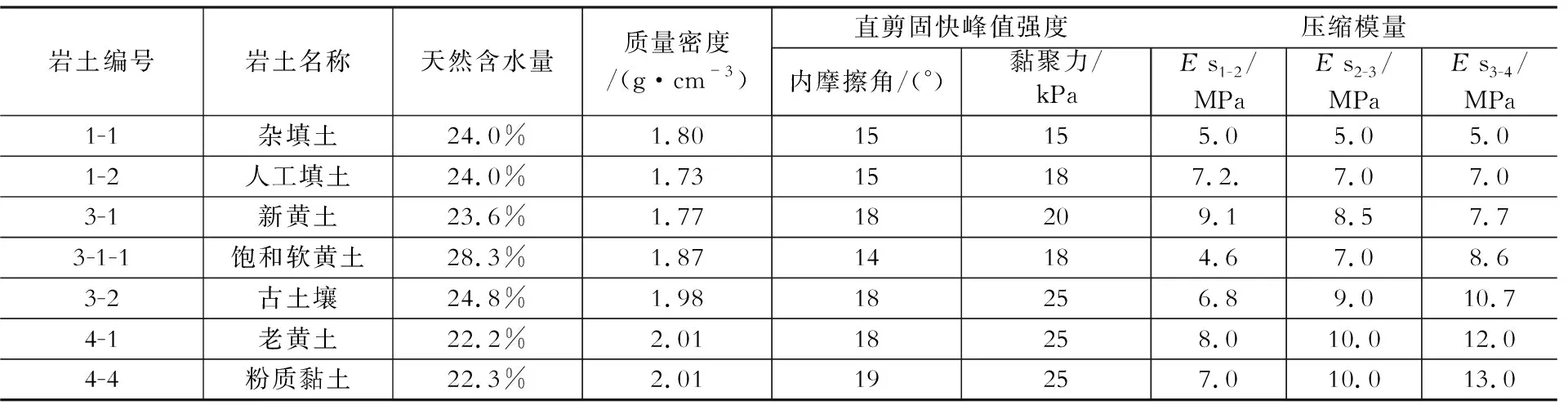
岩土编号岩土名称天然含水量质量密度/(g·cm-3)直剪固快峰值强度内摩擦角/(°)黏聚力/kPa压缩模量Es1-2/MPaEs2-3/MPaEs3-4/MPa1-1杂填土24.0%1.8015155.05.05.01-2人工填土24.0%1.7315187.2.7.07.03-1新黄土23.6%1.7718209.18.57.73-1-1饱和软黄土28.3%1.8714184.67.08.63-2古土壤24.8%1.9818256.89.010.74-1老黄土22.2%2.0118258.010.012.04-4粉质黏土22.3%2.0119257.010.013.0

图3 平面开挖顺序示意图 (单位：m)Fig.3 Sketch of excavation sequence (Unit：m)

3 数值模型建立

3.1 计算模型

数值模型采用Midas GTS大型有限元计算程序建立。结合工程实际情况，确定基坑开挖影响深度为开挖深度的2～4倍，影响宽度为开挖深度的3～4倍，地铁管片侧面影响范围为盾径的4倍，底面影响范围为盾径的3倍，从而确定模型几何尺寸为90 m×45 m×35 m，数值模型如图4所示。模型约束条件地表面为自由面；模型四周约束法向水平方向位移，底面约束(X、Y、Z)3个方向位移，支护桩底约束竖向位移。结构模型采用Mohr-Coulomb屈服准则[8]。土体采用实体单元，地铁管片采用板单元，盾构及土间施加Goodman接触单元[9,10]。模型中土层依据工程场地内实际地层土分布情况取用。

3.2 基本假定

采用Midas GTS进行有限元计算时，为了简化计算，采用如下基本假定[11]：

(1) 同一种材料为均质、各向同性；

(2) 土体为理想弹塑性材料，计算理论模型为摩尔-库伦模型，地铁管片为弹性体；

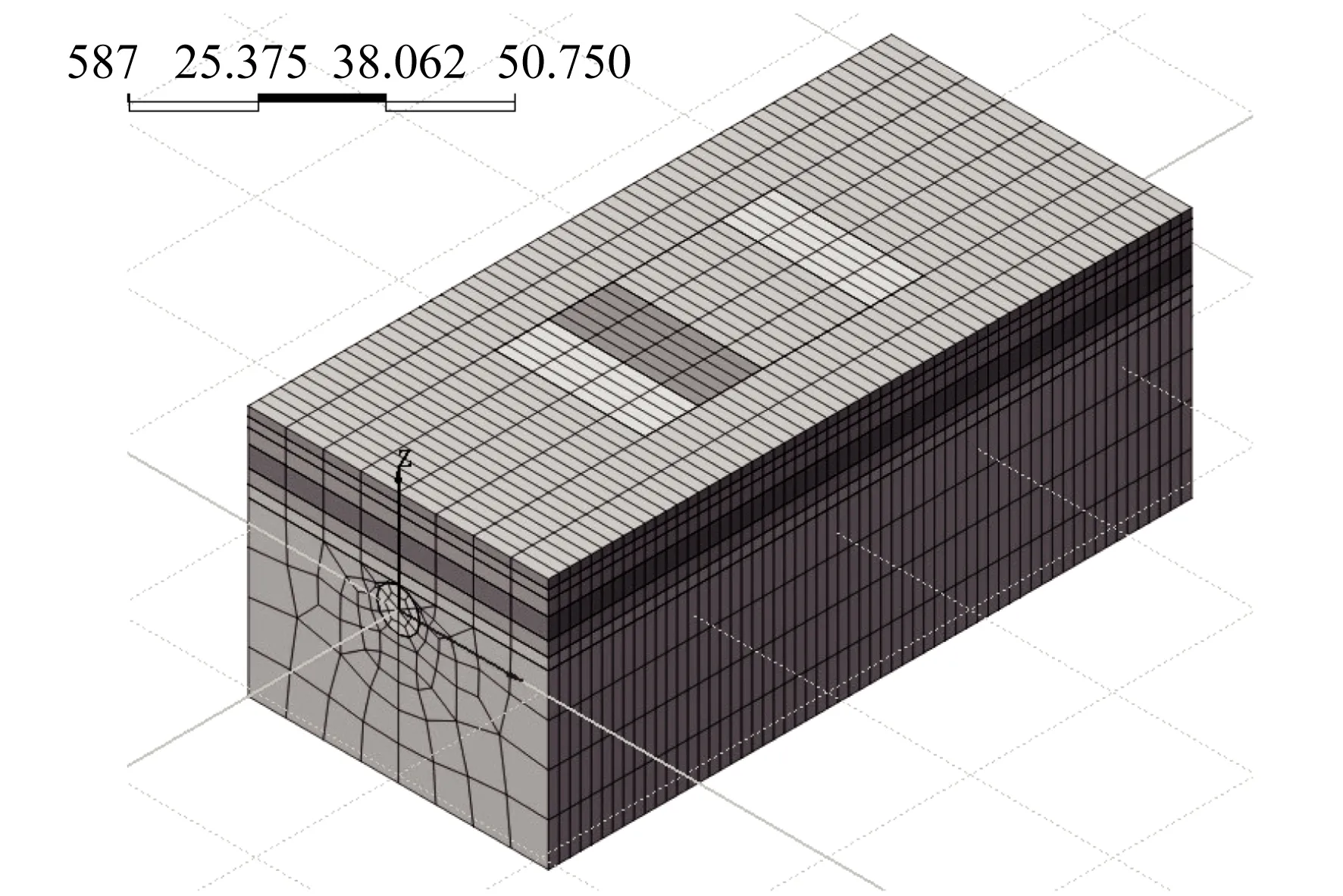
图4 有限元模型示意Fig.4 Finite element model diagram

(3) 因地铁管片周围注浆范围难以确定，故偏安全地不考虑地铁管片外侧的注浆加固范围；

(4) 考虑地铁管片和土体之间的相互作用；

(5) 不考虑土体的排水固结引起的土体设计参数改变；

(6) 不考虑由于基坑开挖施工对土体扰动的影响。

3.3 施工工况

为分析不同施工工况对既有地铁线变形的影响，考察分析5种不同工况下的计算结果。

工况一：原状土不经过旋喷桩地基加固，基坑分四块开挖，每个小块开挖后完成坑内结构施工后不回填。

工况二：原状土不经过旋喷桩地基加固，基坑分四块开挖，每个小块开挖后完成坑内结构施工回填至原地面。

工况三：在工况二的基础上考虑旋喷地基加固的影响，调整复合地基弹性模量(复合地基土弹性模量Ed=500 MPa)，但不调整复合地基黏聚力和内摩擦角。

工况四：在工况三的基础上在既有线两侧增设抗拔桩锚固于南门隧道底板(施工期间在地铁管片两侧3 m安全距离以顺着地铁轴线方向设两排钻孔灌注桩，后期与南门隧道底板固结，以提供运营期间抵抗地铁上隆抗力)。抗拔桩桩径均为1 m，桩长30 m。有限元模型中在前4次开挖阶段仅考虑灌注桩桩底约束竖向位移，施工完成阶段将桩底节点与对应隧道底板节点固结。

工况五：在工况三的基础上不仅调整复合地基弹性模量，同时调整复合地基粘聚力和内摩擦角(复合地基土黏聚力C值取250 kPa，复合地基土剪切角φ=45°)。

4 计算结果分析

4.1 基坑底面隆起变形

5种工况下不同施工阶段(4次开挖及施工完成阶段)基底隆起变形量汇总至图5。工况一的基底隆起变形最大，且随着开挖块数的增加基底隆起逐渐变大，第4次开挖完成后基坑隆起最大值为11.3 cm，施工完成阶段基坑隆起值为8.5 cm，该工况下各阶段基底隆起变形均远超出限值2 cm。工况二采用随挖随填至地面的措施之后，各阶段的基坑隆起值均有一定的减少，第1次开挖完成后基坑隆起最大值为7.9 cm，仍超出基坑变形限值。工况三、四各阶段的基底隆起变形量较工况二大大降低，且均相同。工况三施工完成阶段基底隆起值为1.38 cm。采用抗拔桩措施后，工况四施工完成阶段隆起值减少为0.86 cm，小于基坑变形限值2 cm。工况五各阶段的基底隆起变形量均有一定减少，第3次开挖完成后基坑隆起最大值为0.9 cm，施工完成阶段的基坑隆起也有一定减少，大小为0.21 cm。

4.2 基坑底面沉降变形

5种工况下不同施工阶段基底沉降变形量汇总至图6。从图中可以看出，工况一的基底沉降变形第3次开挖完成后基坑沉降最大值为4.4 cm，施工完成阶段的基坑沉降值为4.2 cm，该工况下各阶段基底沉降变形均远超出限值20 mm。工况二的基坑沉降变形量最大，且随着开挖块数的增加基底沉降逐渐变大，第4次开挖完成后基坑沉降值为10.7 cm，远超出基坑变形限值。工况三、四下各阶段及施工完成阶段的基底沉降变形量均大致相同，工况三、四下随着开挖块数的增加基底沉降逐渐变大，在第4次开挖完成后基坑沉降最大值为1.65 cm，小于基坑变形限值20 mm。工况五下各阶段的基底沉降变形量均有一定减少，第4次开挖完成后基坑沉降最大值为0.67 cm。

图5 基底隆起变形 (单位：cm)Fig.5 Uplift deformation at the bottom of foundation pit(Unit：cm)

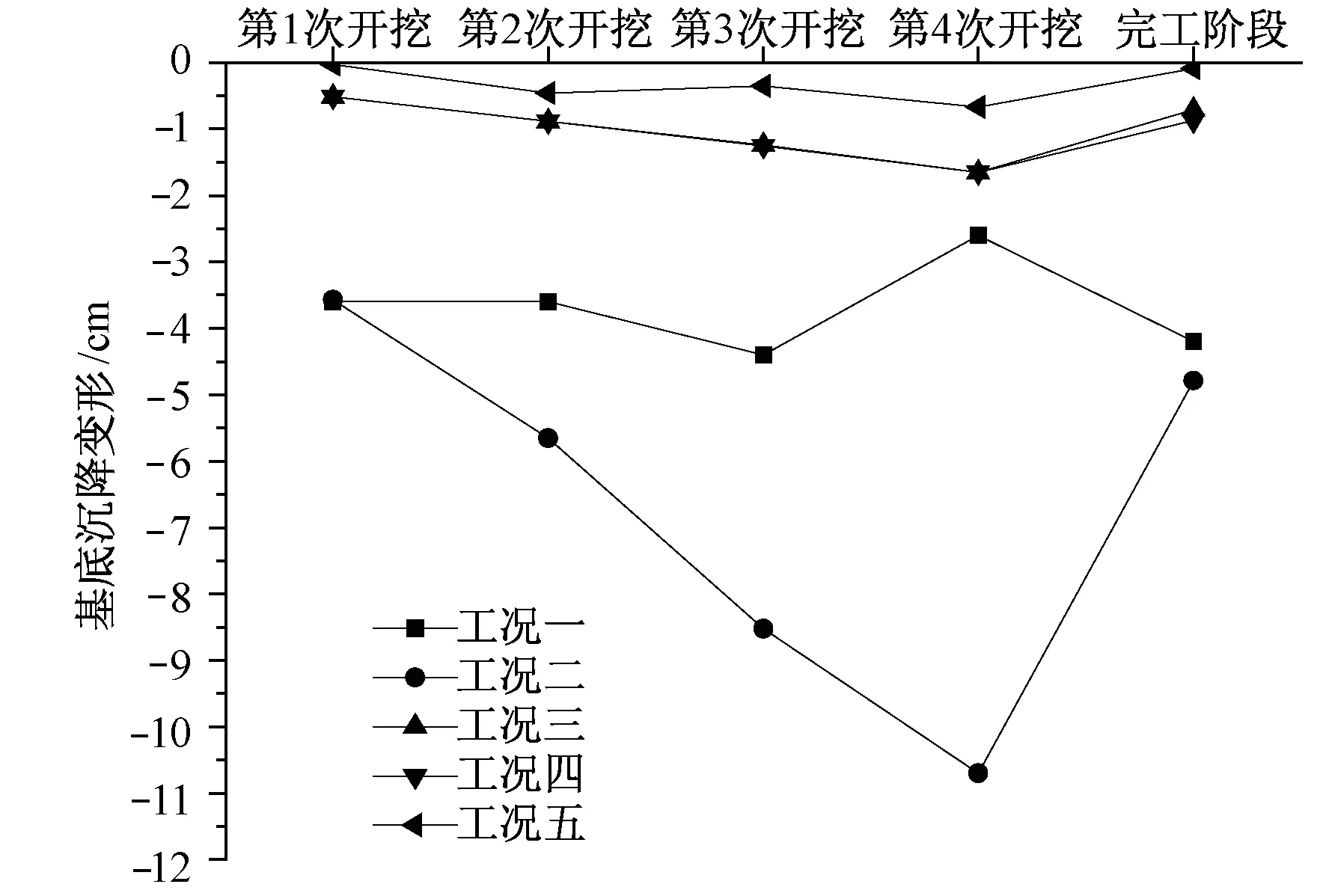
图6 基底沉降变形 (单位：cm)Fig.6 Settlement deformation at the bottom of foundation pit (Unit：cm)

4.3 管片隆起变形

5种工况下不同施工阶段管片隆起变形量汇总至图7。从图中可以看出，工况一的管片隆起变形最大，且随着开挖块数的增加管片隆起逐渐变大。第4次开挖完成后管片隆起最大值为5.81 cm，施工完成阶段的管片隆起值为3.05 cm，参考国内相关资料，确定管片隆起限值为1 cm，该工况下各阶段管片隆起变形均远超出限值。工况二采用随挖随填至地面的措施之后，各阶段的管片隆起值均有一定的减少。第3次开挖完成后管片隆起最大值为2.87 cm，超出管片隆起限值。工况三、四下各阶段的管片隆起变形量均相同，第3次开挖完成后管片隆起最大值为0.9 cm。工况三施工完成阶段的基底隆起值为0.83 cm。采用抗拔桩措施后，工况四施工完成阶段隆起值减少为0.26 cm，均小于管片变形限值。工况五下各阶段的管片隆起变形量均有一定减少，第3次开挖完成后管片隆起最大值为0.77 cm，施工完成阶段的管片隆起也有一定减少，变形为0.17 cm。

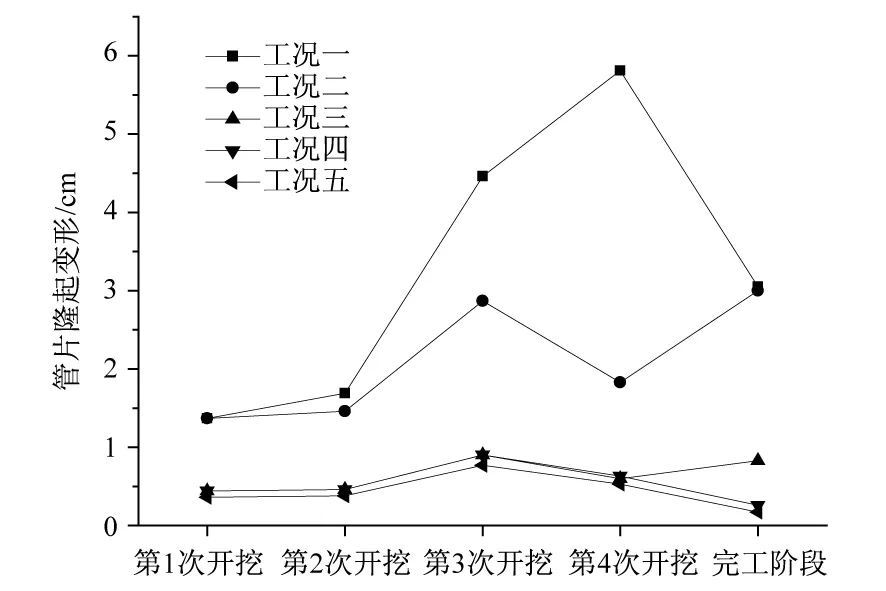
图7 地铁管片隆起变形 (单位：cm)Fig.7 Uplift deformation on tunnel segment (Unit：cm)

4.4 管片沉降变形

5种工况下不同施工阶段管片沉降变形量汇总至图8。从图中可以看出，工况一的管片沉降变形最大，第2次开挖完成后管片沉降最大值为0.4 cm，施工完成阶段下管片沉降为0.25 cm。参考国内相关资料，确定管片沉降限值为1.5 cm。该工况下第2次开挖后管片沉降变形均小于限值。工况二采用随挖随填至地面的措施之后，各阶段的管片沉降值均有一定的减少，营运期间管片沉降值为0.26 cm。工况三、四各阶段的管片下降变形量较工况二有较大减少。采用抗拔桩措施后，工况四施工完成阶段管片沉降值为0.08 cm，均小于管片变形限值。工况五各阶段的管片隆起变形量均有一定减少，第3次开挖完成后基坑隆起最大值为0.008 cm，施工完成阶段下基坑隆起值减少为0.016 cm。

图8 地铁管片沉降变形 (单位：cm)Fig.8 Settlement deformation on tunnel segment (Unit：cm)

5 结 论

通过对本工程的明挖基坑上穿既有地铁线路的有限元模型分析计算可得出以下一些结论：

(1) 对于明挖基坑近接工程，在对原状土不进行处理且不随填随挖的情况下，基坑坑底隆起最大值为11.3 cm，沉降最大值为4.3 cm，均大大超出坑底变形限值；地铁管片隆起最大值为5.81 cm，超出管片隆起变形限值。

(2) 对原状土不进行处理，但是采用随挖随填施工后，各阶段的基坑隆起值均有一定的减少，但基坑沉降值变大，且变形量均超出坑底变形限值；地铁管片最大隆起值及沉降值有一定的减少，变形值仍超出管片隆起变形限值。

(3) 采用旋喷桩加固周边土层之后，基坑坑底变形值及地铁管片变形值均大幅降低，且均小于变形限值。采用抗拔桩加固后，基坑及管片隆起值均有减少，基坑坑底隆起值最大值减少为0.86 cm；地铁管片隆起最大值减少为0.26 cm。

[ 1 ] 孙钧，刘洪州.交叠隧道盾构法施工土体变形的三维数值模拟[J].同济大学学报，2002，30(4): 379-385.

Sun Jun, Liu Hongzhou. 3-D numerical simulation of ground surface settlement under overlapped shield tunneling[J]. Journal of Tongji University，2002，30(4): 379-385. (in Chinese)

[ 2 ] 陶连金，唐四海，金亮. 隧道上穿既有车站结构的变形预测及安全评估[J] .地下空间与工程学报，2008，4(3): 442-447．

Tao Lianjin, Tang Sihai, Jin Liang. Deformation prediction and risk evaluation of the existing subway station structure with above-traversed tunnel[J] . Chinese Journal of Underground Space and Engineering, 2008, 4(3): 442-447. (in Chinese)

[ 3 ] 陈亮，黄宏伟，王如路.近距离上部穿越对原有隧道沉降的影响分析[J]．土木工程学报，2006，39(6): 83-87．

Chen Liang, Huang Hongwei, Wang Rulu. Analysis of the observed longitudinal settlement of a tunnel caused by an adjacent shield tunneling on top[J]. China Civil Engineering Journal, 2006, 39(6): 83-87. (in Chinese)

[ 4 ] 刘树佳，张孟喜，吴慧明，等.新建盾构隧道上穿对既有隧道的变形影响分析[J]．岩土力学，2013，34(1): 399-405．

Liu Shujia，Zhang Mengxi，Wu Huiming, et al. Deformation effect on existing tunnels overlapped by new tunnel in lower-region[J]. Rock and Soil Mechanics, 2013, 34(1): 399-405. (in Chinese)

[ 5 ] Yazdchi M, Yeow H C, Young S. 3D finite element prediction of ground movement induced by tunneling operation in London clay[J]. Computing in Civil Engineering, 2005, 7: 251-259.

[ 6 ] 廖少明，杨俊龙，奚程磊，等.盾构近距离穿越施工的工作面土压力研究[J].岩土力学，2005，27(11): 1727-1730.

Liao Shaoming, Yang Junlong, Xi Chenglei, et al. Approach to earth balance pressure of shield tunneling across ultra-near metro tunnel in operation[J]. Rock and Soil Mechanics, 2005, 27(11): 1727-1730. (in Chinese)

[ 7 ] 胡群芳，黄宏伟.盾构下穿越已运营隧道监测与技术分析[J].岩土工程学报,2006,28(1):42-47.

Hu Qunfang, Huang Hongwei. Analysis and monitoring on sheild tunneling under existing adjacent tunnel[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(1): 42-47. (in Chinese)

[ 8 ] 张晏齐,张伟平,顾祥林,等.相邻施工影响下砌体结构基础变形控制参数的比较分析[J].结构工程师,2012,28(6): 108-112.

Zhang Yanqi, Zhang Weiping, Gu Xianglin, et al. Comparative study on control parameters for foundation deformation of masonry structures caused by adjacent underground construction[J]. Structural Engineers，2012, 28(6): 108-112. (in Chinese)

[ 9 ] 董辉,马一跃,聂志红,等.戈壁土路基后期沉降预测方法及误差分析[J].湘潭大学自然科学学报,2012，34(1): 48-53.

Dong Hui, Ma Yiyue, Nie Zhihong, et al. On prediction method and accuracy of post-construction settlement for the Gobi roadbed on Lanxin passenger line[J]. Natural Science Journal of Xiangtan University, 2012, 34(1): 48-53. (in Chinese)

[10] 信春雷,高波,李苍松.深埋高水位山岭隧道支护与衬砌外水压力分析[J].公路交通科技,2013,30(2): 77-82.

Xin Chunlei, Gao Bo, Li Cangsong. Analysis of external water pressure on support and lining of deep mountain tunnels below high water table[J]. Journal of Highway and Transportation Research and Development, 2013, 30(2): 77-82. (in Chinese)

[11] 陈骥.地铁区间暗挖隧道风险评估体系研究[J].结构工程师,2012,28(3): 152-157.

Chen Ji. Research on risk assessment system of subsurface excavation tunnel[J]. Structural Engineers, 2012, 28(3): 152-157.(in Chinese)