从矩形的折叠说开去——对一道中考选择题的探究

●张 红 (长兴县教育研究中心 浙江长兴 313100) ●高 峰 (长兴县小浦中学 浙江长兴 313100)

2013年中考已完美落幕，仔细分析2013年浙江省湖州市中考数学卷选择题的第9题，回味无穷.

1 原题再现

如图1，已知四边形ABCD是矩形，把矩形沿直线 AC折叠，点B落在点E处，联结DE.若DE ∶AC=3 ∶5，则AD ∶AB的值为 ( )

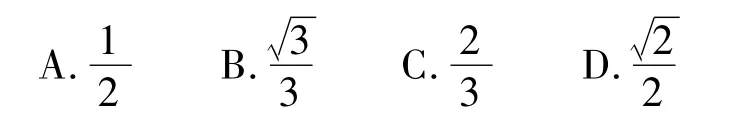
图1

2 试题探究

2.1 命题意图

2.1.1 考查试题类型

纵观湖州市以及其他省市历年的数学中考试题，涉及图形三大变换的题型屡屡出现，其中在利用图形的折叠即轴对称变换的大背景下，要求学生通过对图形变换前后进行分析对比，进而找到隐含的线段数量或位置关系，结合已有的知识或条件进行推理论证的题型，更是屡见不鲜.

2.1.2 考查知识内容

本题主要考查的知识内容：轴对称变换、平行线、等腰三角形、直角三角形、相似三角形及矩形的判定和性质等，此题属于稍难题.

2.1.3 考查基本图形

基本图形来源于浙教版《数学》八年级下册第6.1节“矩形(1)”作业题A组的第4题.

2.1.4 考查思想方法

转化思想、类比猜想、数形结合思想.

2.2 试题解答

本题很难直接寻求AD ∶AB的值，因此在解决本题时，应从条件入手.由DE ∶AC=3 ∶5，很容易想到相似，再通过对题目的深入挖掘，加以大胆猜想、尝试、转化，得到DF ∶FC=3 ∶5，继而得到DF∶AF=3∶5，把比例关系集中到一个直角三角形中，得到DA∶DC=4∶8，从而顺利转化为DA ∶AB=1 ∶2.

解法1 因为 ∠EAC=∠CAB=∠DCA，所以 AF=CF.

又△DAC≌△ECA且有公共边AC，故这2个全等三角形AC边上的高相等，从而

可得△DEF∽△CAF，于是由△DAF为直角三角形可知

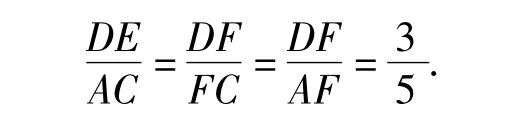
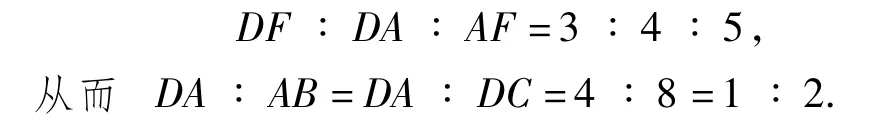
解法2 如图2，过点D，E分别作 AC的垂线 DG，EH，令DE=3x，AC=5x，由解法 1 可知四边形DACE为等腰梯形，则

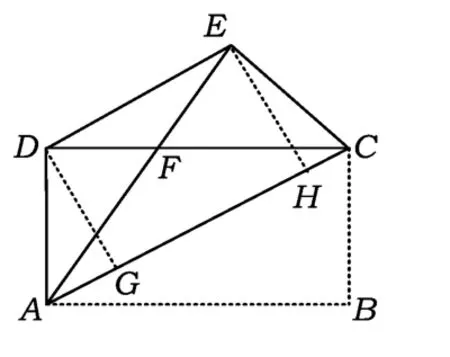
图2

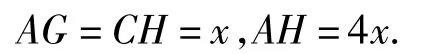
根据射影定理，因为

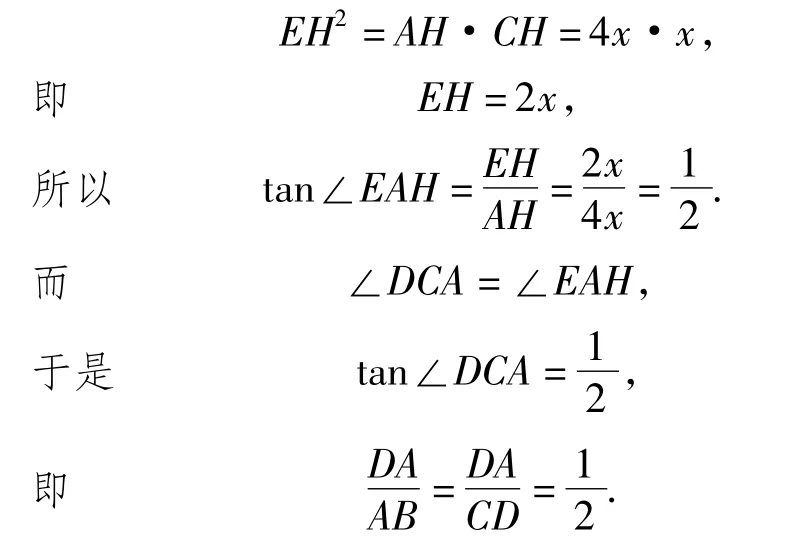
2.3 试题拓展

2.3.1 原题探究

探究1 求点F到AC的距离FG与AD，AB之比?

解如图 3，因为已证AF=CF，且 FG⊥AC，所以

图3

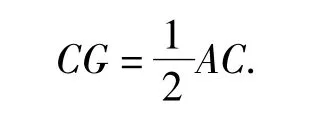
又易证△CFG∽△CAD，则

评析 本题在原题基础上增加了FG与AD，AB的比例关系的求解，加深了对原题的理解.通过AD设元，根据△CFG∽△CAD，建立FG与AD的比例关系求解，得到FG与AD，AB之比.

探究2 若AD=4，AB=8，求重叠部分的面积?

解法1 根据探究1的结论：

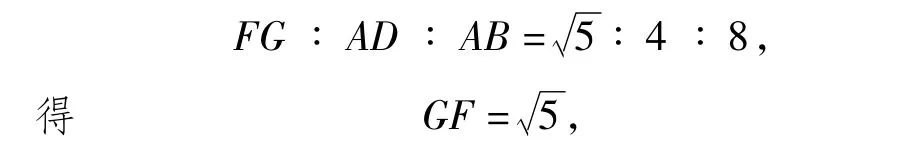
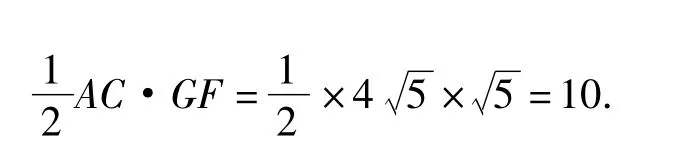
解法 2 设 CF=AF=x，则 DF=8-x，而△ADF是直角三角形，则

解得x=5，即CF=5，因此△AFC的面积为

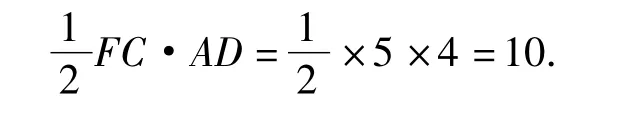
评析 本题注重对折叠后面积的探讨，根据比例关系或者利用勾股定理设元建立方程求解，使本题得到解决.

探究3 如图4，若BC=3 cm，DC=4 cm，

(1)求EF的长;

(2)联结 DE，求四边形ACED的面积与周长各是多少?

解(1)因为四边形ABCD为矩形，BC=3，DC=4，所以将矩形ABCD沿对角线AC折叠，使点B落在点E处，则

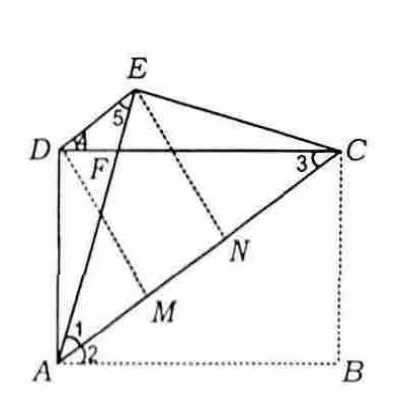
图4

(2)由第(1)小题可知：AF=CF，∠1=∠3，因为AE=CD，所以

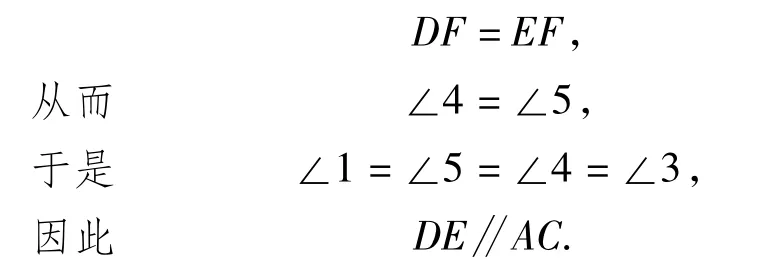
因为AD=CE=3，且AD与CE不平行，所以四边形ACED是等腰梯形.过点D，E分别作DM⊥AC于点M，作EN⊥AC于点N，则四边形DMNE为矩形，从而

评析 本题通过对折叠之后四边形的面积和周长的探究，使学生对折叠后图形的整体性认识更加全面.

探究4 将原图置于坐标系中，若C(8，4)，求点E的坐标?

解如图5，过点E作x轴的平行线交y轴于点M，交BC延长线于点N.设E(a，b)，则

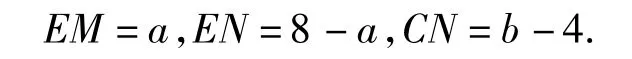
根据K型相似，易知△AME∽△ENC，则

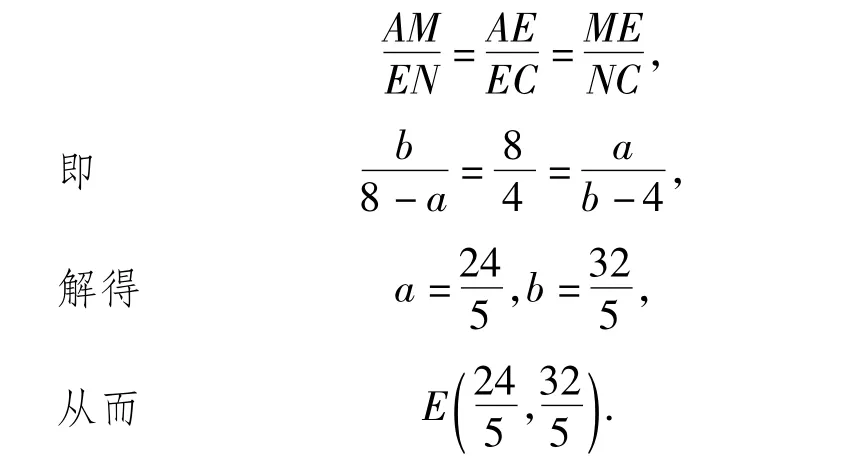
评析 本题将原图形放置于坐标系中，综合性考查更加全面，建立相似关系，得出比例式是关键.

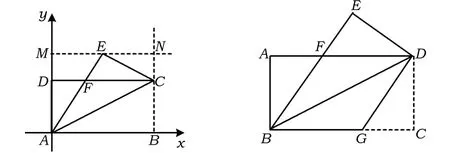
图5 图6

探究5 如图6，若将折叠的图形恢复原状，点F与BC边上的点G正好重合，联结DG.

(1)试判断四边形BGDF的形状，并说明理由;

(2)若 AB=4，AD=8，求线段 DG 的长.

分析(1)根据平行线的性质和折叠不变性求出2个角相等，再判断出2条边相等;判断出四边形BGDF是平行四边形，再根据BG=BF，得出四边形BGDF是菱形.

(2)设 AF=x，则 BF=FD=8-x，利用勾股定理即可求出DF的长，即为DG的长.

解(1)BF=DF.因为FD∥BC，所以

由折叠不变性知

而FD∥BG，于是四边形BGDF是平行四边形，又BG=BF，从而四边形BGDF是菱形.

(2)设 AF=x，则

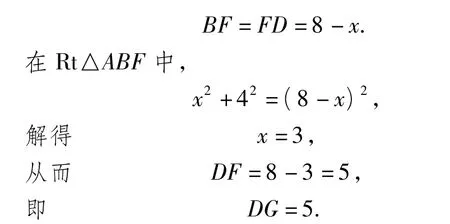
评析 本题将原图形还原，更加注重折叠前后的对比，从错综复杂的数量关系中找出不变量，通过等量代换得出四边形BGDF是菱形，以及建立方程求出线段DG的长是解题的关键.

2.4 解题策略

通过对矩形沿对角线折叠问题的深入研究，发现问题虽然不尽相同，但是解题的方法却大同小异，具体解题思路可以归纳为以下几个方面：

(1)认清折叠的本质即轴对称变换，通过“折”这个过程，仔细观察折之前和折之后角、线段发生的变化，从变化过程中发现并找出相应的数量及位置关系特别是等量关系，也就是从变中找出不变.

(2)重视“叠”的结果，观察折叠之后的新图形有没有构造出新的特殊图形(等腰三角形、直角三角形、平行四边形、等腰梯形等).

(3)在折的过程中发现的有用信息，通过等量代换或相应的变形转化集中在叠之后的特殊图形中，根据特殊图形的特殊关系建立相应的等式.例如：若是直角三角形，则通过勾股定理建立方程;若是相似三角形，则通过比例关系建立比例关系式，进而求解.

实际上，对图形的变换类型习题进行分析讲解和联想探究过程中，蕴藏着巨大的命题效益，许多中考试题就是由一些基本变换习题变式和拓展得来的.同时，这些题目虽来源于课本，但又高于课本，对其分析讲解可以以点带面，举一反三，触类旁通，有效地提高学生的解题应变能力，也可培养教师归纳概括及创新能力.

［1］ 费志良.与矩形有关的几个折叠问题［J］.中学生数学，2006(12)：10-12.

［2］ 胡怀志.中考中常见的矩形折叠问题［J］.数学大世界，2010(9)：7-9.

［3］ 黄建阳.几种常见折叠问题［J］.数理化学习，2012(3)：10-12.