对冲式止回阀低流量关闭过程动态特性分析

杨志达，陈炳德，黄伟，韩伟实，张志明

(1.中国核动力研究设计院核反应堆系统设计技术重点实验室，四川成都610041;2.哈尔滨工程大学核科学与技术学院，黑龙江哈尔滨150001;3.中国核电工程有限公司，北京100840)

为了增加动力装置的生命力，在每条回路中设置了2台泵，由于这一特殊结构，必须在每台泵出口处设置止回阀以防止冷却剂倒流［1］。同时要求阀门的关闭速度不能过快，否则可能会引起严重的水锤现象，造成管道、泵等设备的严重损坏。另外，还需要止回阀有一定的泄漏量，否则开启备用回路时会对其造成一定的热冲击，引起材料热疲劳。由此可见，止回阀的作用在动力装置中非常重要。目前常见的止回阀有旋启式、双碟式、升降式、斜碟式，这些止回阀的流体运动方向与阀头运动方向一致，可能导致严重的水锤现象和阀头与阀座的撞击。如果流体运动方向与阀头运动方向相反，则阀头会与流体相互形成阻尼，将会大大减弱水锤现象和阀头与阀座的撞击。本文利用此原理研制了对冲式止回阀，其抑制水锤和阀头与阀座撞击能力较好，高流量下启闭特性较好，但低流量下关闭可靠性不高，需要对其关闭过程的动态特性应用计算流体力学技术进一步研究。

1 模型的建立

图1为动力装置实验系统简图，为增加可靠性，设置了2台泵。当1号泵停闭后开启2号泵时，1号止回阀应可靠关闭，否则部分冷却剂会在1号泵和2号泵之间形成小循环，防止造成事故。

图1 动力装置系统简图Fig.1 Sketch of power unit system

1.1 原理

对冲式止回阀结构图如图2［2］，对冲式止回阀利用差动活塞实现阀头与流体的对冲运动。所谓对冲运动是指阀头的运动方向与流体的流动方向相反，止回阀在流体顺流时能够快速开启，在流体逆流时阀头能与流体相互形成阻尼，并完成关闭运动。

图2 止回阀结构图Fig.2 Structure map of DC check valve

对冲式止回阀的阀头关闭驱动力主要是由冲压腔内侧、冲压腔外侧和阀头前端3个区域所形成的压差提供的［3-4］。当流体顺流开启时，流体经过阀头与阀体的节流作用后压力下降，所以阀头前端处于低压区，因冲压腔内侧与冲压管相通，冲压管开口处于低压区，故冲压腔内侧为低压区，而冲压腔外侧位高压区，且因活塞直径大于阀头直径，所以作用于阀头上的合力指向开启方向，阀门打开。阀头的移动方向与流体流动的方向相反。

当流体逆流关闭时，冲压腔内流体速度很低，压力近似于滞止压力，所以处于高压区，而阀头前端和冲压腔外侧流体速度较快，处于低压区，且活塞直径大于阀座直径，所以作用于阀头上的合力指向关闭方向，阀门关闭。阀头的运动方向与流体的流动方向相反。另外，阀座是可活动的，在流体节流作用下，可加速阀门的关闭。

1.2 动力学模型

阀头上的压差取决于阀内流场的压力分布，该压差产生阀头赖以完成启闭动作的驱动力，而阀头的运动直接影响阀内流场，流场的变化又反过来影响阀内流场的分布。如图3所示，是利用CFD技术模拟对冲式止回阀启闭动态过程的程序流程图，对冲式止回阀的动态过程是一个耦合的闭环过程，需用数值计算的方法求解。

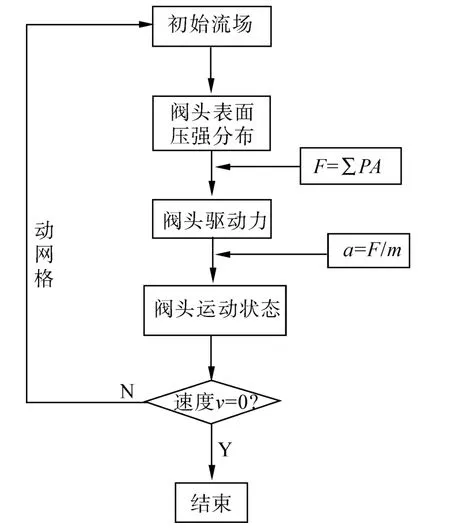
图3 DC止回阀动力学流程图Fig.3 Dynamics flow diagram of DC check valve

由于止回阀的结构较复杂，导致其流场、压力场分布也比较复杂，所以在建立流道时进行了必要简化。根据图3中所示压力分布、阀头驱动力以及阀头运动速度的耦合关系，可以得到阀头阀座的受力方程。阀头、阀座的受力方程遵循牛顿第二定律，其中阀座比阀头多弹簧的推力。以下为阀座的力学方程。

根据牛顿第二定律，有

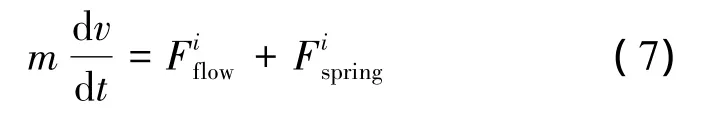
其差分格式和边界条件为

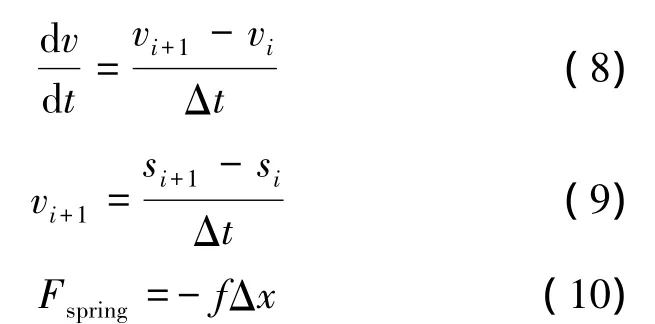
式中:m为阀座质量，kg;Fflow为流体作用力，N;Fspring为弹簧作用力，N;vi为阀头在i时刻的速度，m/s;si为阀头在i时刻的位移，m;k为弹簧系数，N/m。

将以上运动方程编译成Fluent用户自定义文件(UDF)程序，与FLUENT相连接定义阀座的运动状态。阀头的运动程序参照阀座的运动程序，需将弹簧的系数k定义为零。

1.3 数值计算与边界条件

采用有限体积法求解，压力项用标准格式离散，其余都用一阶迎风格式离散，压力速度耦合方式用SIMPLE算法求解。进出口边界类型设定为压力进口和出口，进口压力100 kPa，出口压力96 kPa。工作压力设定为 101.325 kPa。计算流体的密度为 998.2 kg/m3，粘性系数为 0.001 N·s/m3。湍流强度 0.03，水力直径0.28 m，动网格弹性系数 0.8，边界松弛因子 0.8。

2 动网格的生成

对冲式止回阀在关闭过程中流域形状不断发生改变，其动态过程可通过对比不同工况下阀头、阀座所受的力和速度的变化分析。通过对比不同工况下的冷却剂流量变化判断阀门的关闭特性，这样可确定不同状态下的阀门工作状态。利用FLUENT中动网格设置以及欧拉显式方程编写UDF程序，通过流场分析对阀头阀座进行动态分析，可对对冲式止回阀的关闭过程实现动态可视化模拟［6-7］。

2.1 动网格技术

所选的网格为三角形和正四面体，所以采用弹簧近似光滑模型，但此模型不能用于运动变化幅度较大的模型。为了保证网格在更新过程的可靠性，还选用了局部网格重划模型，确保阀头、阀座运动较大时网格不出现负体积。

流场控制模型是基于流域固定形状的情况，当采用动网格技术后，计算区域是变化的，所以要对上述流场控制模型进行改造，即考虑动边界移动的影响［8-10］，表达式如下:

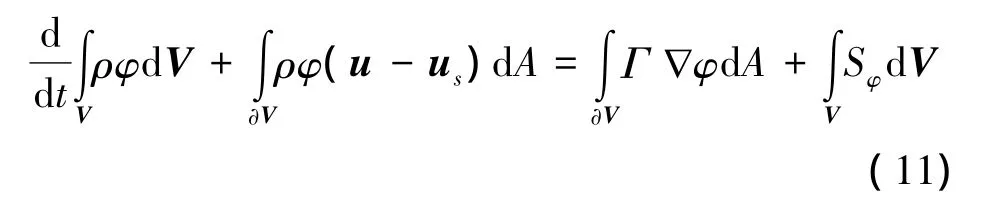
式中:ρ为液体的密度，kg/m3;u为液体的速度矢量;us为动网格的网格变形速度;Γ为扩散系数;A为控制体表面积;Sφ为通量的源项φ;∂V为控制体V的边界。

2.2 UDF 程序

对冲式止回阀的关闭过程即力的平衡过程，对其进行关闭过程的动态研究，需要首先对其进行受力过程分析，根据止回阀的结构尺寸建立其全开三维实体模型，选择相应的计算模型，根据阀座和阀头的运动情况，通过适时地生成和消亡网格更新计算区域，完成阀门关闭过程的模拟。利用牛顿第二定律的欧拉显式方程式:

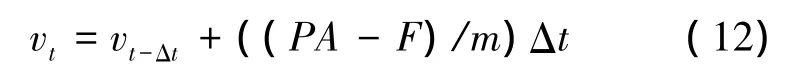
式中:vt为t时刻阀头速度，m/s;vt-Δt为阀头 Δt时刻前速度，m/s;P为阀头所受压强，Pa;A为阀头面积，m2;F为所受到的反向力，N;m为阀头质量，kg;Δt为时间间隔，s。由式(12)描述阀头和阀座运动，通过编译动网格UDF自定义宏，对每一时间步中的节点位置进行更新。

3 模拟结果及分析

为了研究对冲式止回阀关阀动态过程，模拟了其内部压力云图、速度场、流量特性、阀头阀座受力情况。通过对比不同压差下阀头、阀座受力以及速度变化，分析阀头、阀座的运动情况。通过对比不同压差下阀门的流量变化判断阀门的关闭特性，可清楚地了解不同状态下阀门的工作状态。模拟中选取的压差分别为2、3、4、5 kPa 4种情况进行分析。

3.1 阀内的流场分布

如图4为对冲式止回阀关闭时的静压云图，由图可以看出，流体流动方向为逆流，止回阀关闭以后，压力腔、冲压管内部以及右侧管道为高压区，左侧管道为低压区，如此可保证阀门处于关闭状态，直到流体向右反向流动时阀门被打开。如果流体运动方向为顺流，则冲压管内部与压力腔内部为低压区，靠活塞与阀头面积之差所产生的力使得阀头向左侧运动。

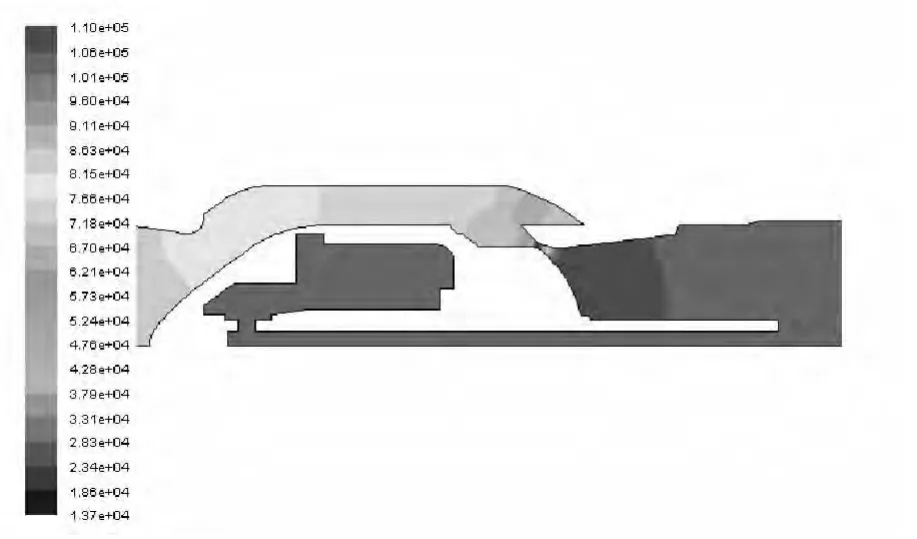
图4 对冲式止回阀关闭时的静压云图Fig.4 Static pressure nephogram of DC check valve closed

3.2 流量特性

流量特性是阀门重要性能指标，图5给出了对冲式止回阀在关闭过程中，不同压差下阀门关闭时入口流量的数值模拟结果。

由图5可知，随着压差的增大流量变化剧烈。压差越大，初始流量也越大，剩余流量也越大。从动态过程来看，流量在阀关闭过程中先缓慢变化，然后急剧减小。这是由于阀头阀座的运动速度逐渐增大所致。在关闭过程结束时，存在剩余流量。这是由于对冲式止回阀关闭过程中，阀头阀座在阀门开度较小时速度较大，单位时间步长内的运动距离较大而造成的。另一个原因是FLUENT的计算区域必须要有网格，所以只能模拟到阀门开度很小的情况。

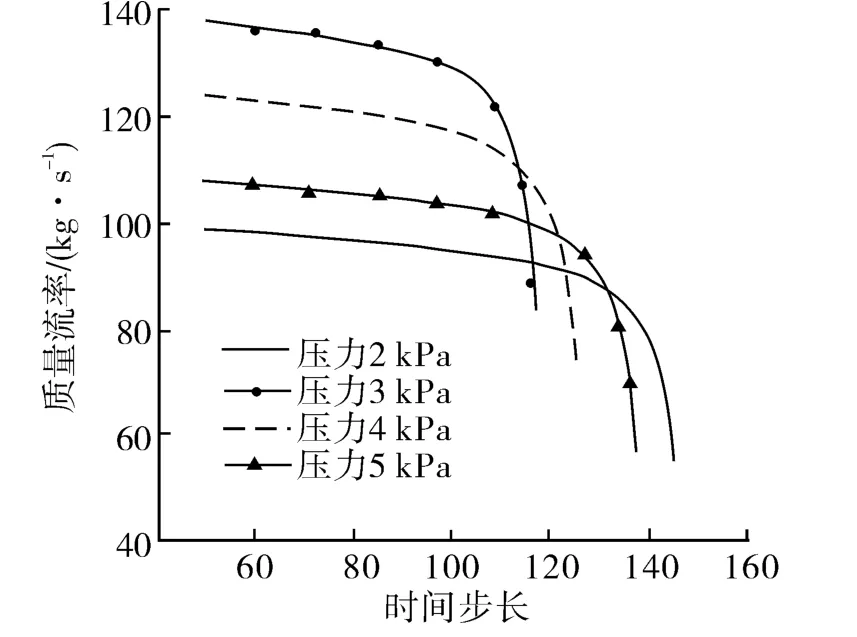
图5 对冲式止回阀流量图Fig.5 Chart of mass flow rate

3.3 阀头阀座分析

图6为4种不同压差下阀头、阀座的受力图，由图可知随着压差的增大，阀头阀座所受到的力在增大。阀门的开度越小，阀头阀座力的变化越剧烈。且随压差的增大，阀门的关闭时间也越短。

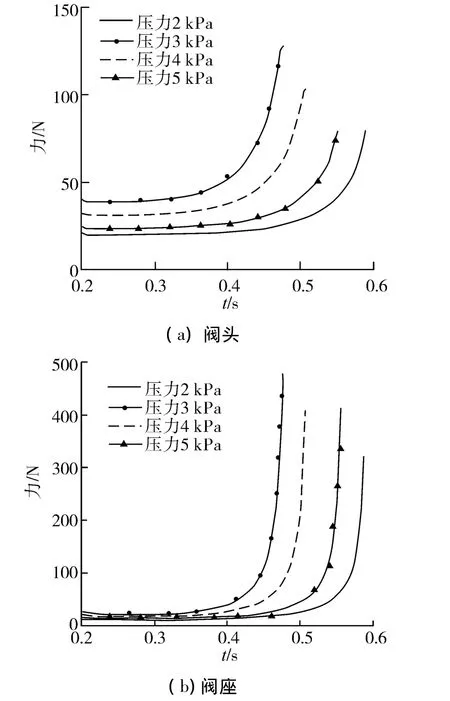
图6 对冲式止回阀阀头、阀座受力图Fig.6 Force diagram of DC check valve head and seat

图7为阀头、阀座速度变化曲线，由图可知，阀头、阀座速度与压差和开度有关，随压差增大而增大，随开度减小而增大。

4种压差下阀头、阀座受力，阀头、阀座的最大速度，起始流量及剩余流量的数值如表1所示。

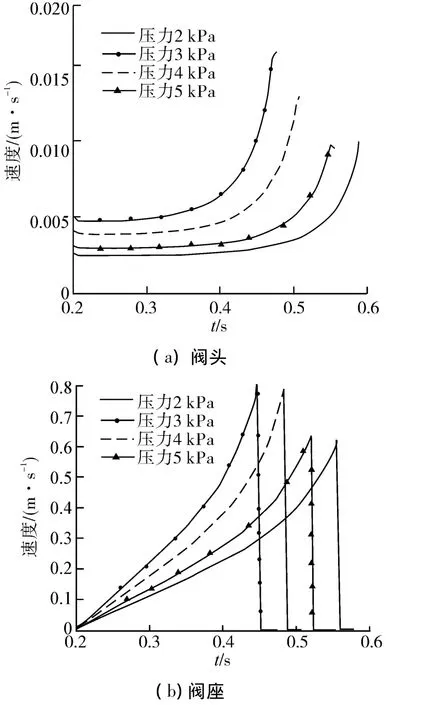
图7 对冲式止回阀阀座速度图Fig.7 Velocity diagram of DC check valve head and seat

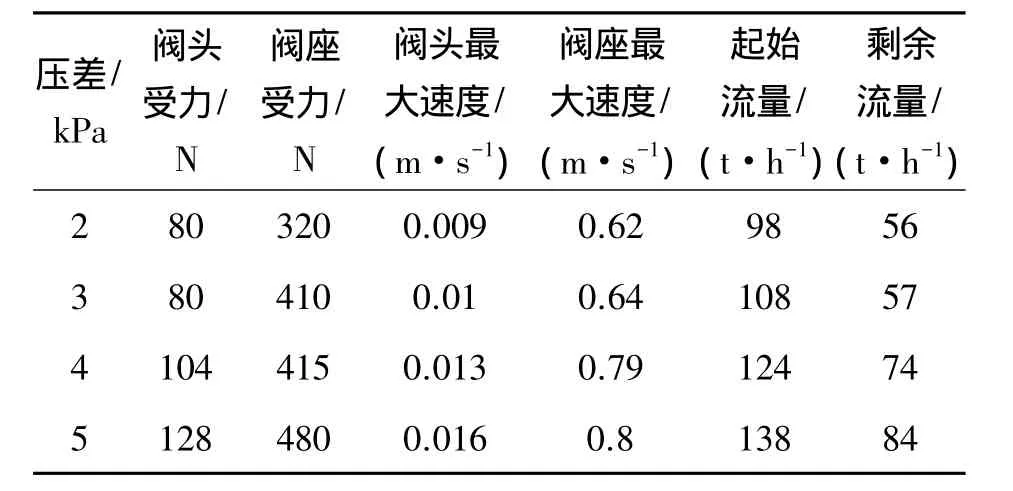
表1 不同压差下阀头、阀座参数Table 1 Parameter of valve head and seat at different pressure

4 实验结果与分析

实验按图1所示的回路建立实验台架，2台泵分别由2台变频器控制转速，从而控制泵流量。测点主要有1、2号阀阀前、阀内、阀后的压力以及回路的流量。通过这些数据可以对阀的运动特性进行分析。阀的关闭状态通过3种方法来判断:

1)通过主环路的电磁流量计进行判断。通过对比实验流量和在该频率下的理论流量来判断阀的关闭程度，2个值接近时表明阀门已将关闭。

2)通过阀头关闭时的声音判断其运动情况。阀门关闭时会听见一声很小的水击声，若听见此声音则表明阀门已关闭，否则没有关闭。

3)通过阀体上的观察孔进行观察。通过观察和标记阀头阀座的位置来判断。

为得到流量和压差的关系，选取了流量分别为0、100、200、300、400、500、600 t/h 的节点分析。选取节点上阀前、阀后压力，计算得出前后压差，得到表2［11］。

表2 不同流量止回阀前后压力及压差Table 2 Pressure before and after valve and pressure difference at different flow rates

实验的关闭时间大致在5 s左右，比计算时间大很多(计算时间不超过1 s，而且压差越大，关闭时间越短，压差为4 kPa时阀门的关闭时间为0.508 s)。这是由于没有考虑滑动套与冲压管之间的摩擦造成的，另外，双泵切换时流体的换向需要一定时间也造成了关闭时间的延迟。

5 结论

通过对对冲式止回阀的动态计算和分析可得到如下结论:

1)阀座的运动对于阀头受力有很大影响。随着阀座的关闭运动，阀头所受的瞬态力逐步增大，阀门的关闭会越来越快，增加了阀门关闭的可靠性。

2)对不同压差下对止回阀的动态计算结果的分析表明，随着阀门开度减小，阀头、阀座受力不断增大，阀头、阀座速度不断增加。阀座受力和速度远远大于阀头受力和速度。阀门所受压差越大，关闭时间越短。

3)试验中关闭时间在5 s左右，远大于计算时间是由于实验过程阀头、阀座的运动受到滑动套与冲压管之间滑动摩擦力的影响，在计算中没有考虑此影响。另外，双泵切换有时间差会造成流体换向时间延迟，也会影响关闭时间。

4)低流量下对冲式止回阀关闭的可靠性依然是其面临的主要问题，还需参数敏感性分析进行优化设计以及实验两方面加以解决。

［1］庞凤阁，彭敏俊.船舶核动力装置［M］.哈尔滨:哈尔滨工程大学出版社，2000:22-24.PANG Fengge，PENG Minjun.Shipping nuclear power plant［M］.Harbin:Harbin Engineering University Press，2000:22-24.

［2］韩伟实，沈明启，韩旭，等.对冲式止回阀:中国，200610010014.7［P］.2006-05-08.HAN Weishi，SHEN Mingqi，HAN Xu，et al.Contra-motion check valve:China，200610010014.7［P］.2006-05-08.

［3］韩旭，周羽.对冲式止回阀原理及启闭特性分析［J］.核动力工程，2006，7(1):66-69.HAN Xu，ZHOU Yu.Principle and opening-closing character analysis of DC check valve［J］.Nuclear Power Engineering，2006，7(1):66-69.

［4］HAN Xu，ZHENG Mingguang，YU Yiqi.Hydrodynamic characterization and optimization of contra-push check valve by numerical simulation［J］.Annals of Nuclear Energy，2011，38(6):1427-1437.

［5］莫乃榕.工程流体力学［M］.2版.武汉:华中科技大学出版社，2009:74-75.MO Nairong.Engineering fluid mechanics［M］.2rd ed.Wuhan:Huazhong University of Science and Technology Press，2009:74-75.

［6］冯进，张慢来.安全阀水动力特性的CFD模拟和研究［J］.核动力工程，2007，28(5):31-34.FENG Jin，ZHANG Manlai.Study on hydrodynamic characteristics of safety valve based on CFD caluculation［J］.Nuclear Power Engineering，2007，28(5):31-34.

［7］江帆，陈维平.润滑用齿轮泵内部流场的动态模拟［J］.现代制造工程，2007(6):116-118.JIANG Fan，CHEN Weiping.Dynamic simulation of flow field inside of lubricate gear pump［J］.Modern Manufacturing Engineering，2007(6):116-118.

［8］王瑞金，张凯，王刚.FLUENT技术基础与应用实例［M］.北京:清华大学出版社，2007:191-195.WANG Ruijin，ZHANG Kai，WANG Gang.FLUENT technology base and applying［M］.Beijing:Tsinghua University Press，2007:191-195.

［9］BATINA J T.Unsteady Euler algorithm with unstructured dynamic mesh for complex-aircraft aerodynamic analysis［J］.AIAA Journal，1991，29(3):327-333.

［10］BATINA J T.Implicit flux-split Euler schemes for unsteady aerodynamic analysis involving unstructured dynamic meshes［R］.N91-10918，1990.

［11］张志明.一回路主止回阀结构优化及流体力学分析［D］.哈尔滨:哈尔滨工程大学，2011:65-66.ZHANG Zhiming.Structure optimization and analysis on fluid mechanics of the primary check valve［D］.Harbin:Harbin Engineering University，2011:65-66.