单侧有限宽度开缝竖通道内的旋转热流体特性
霍岩,邹高万,李树声,郜冶
(哈尔滨工程大学航天与建筑工程学院,黑龙江哈尔滨150001)
高层建筑玻璃幕墙、楼梯井等竖直通道内火灾中,很容易由于火源的自然引射空气来流而引发旋转火焰[1],并且通道空间的开口通风情况会对旋转火焰的生成、维持和溃灭过程产生影响[2]。Chow等[3-5]通过实验证明了具有单侧和双侧开缝的竖直通道内可在开缝宽度与火源满足一定关系的条件下靠火焰的自然引射空气流而形成旋转火焰。然而,以往的研究都是基于竖通道的侧开缝自下至上宽度始终保持一致的情况,但是在建筑火灾等实际情况中,通道的侧开缝宽度自下至上可能是非均匀的,因而会对通道内旋转火焰及其热流场产生不同的影响,本文在确定可形成旋转火焰的单侧开缝竖直通道环境前提下,研究在通道壁面侧开缝部分受限条件下的旋转热流场。所得结论对于深入理解有限开口空间内的旋转火焰特性及与边界条件的关系有一定意义。
1 单侧开缝竖直通道内热流场实验
1.1 实验装置
如图1所示,实验竖直通道内部空间尺寸为:长2.1 m(X),宽 2.1 m(Y),高 9.0 m(Z)。竖直通道由木框搭建外罩白铁皮,前端镶嵌玻璃观察窗。通道顶端竖向开口自然开放。通道的一侧壁面有一宽度d可调的缝隙,可使通道内火焰发生旋转[4]。在通道中心轴线上设置温度测点M1~M8(图1(b))。
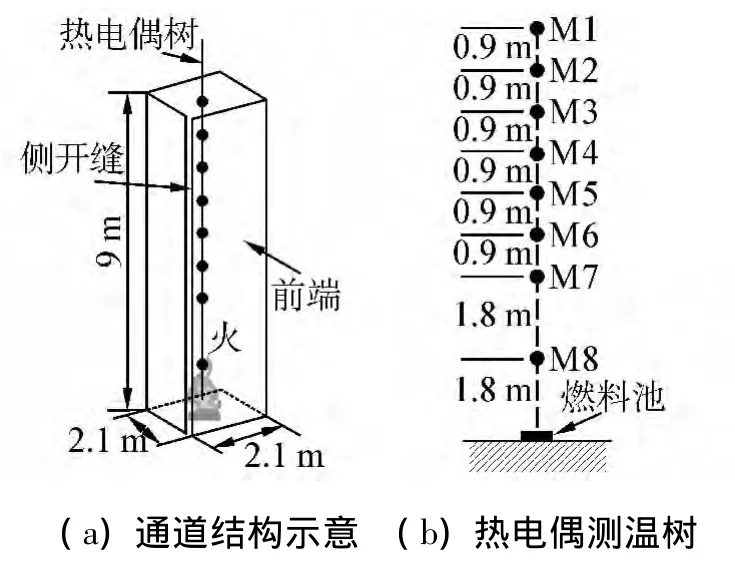
图1 竖直通道实验装置示意图Fig.1 Experimental apparatus of vertical shaft
实验竖直通道的最底部中心地面放置一直径为0.46 m的圆型液体燃料池,池边沿高0.15 m。每条次实验燃料用量均为3L 90#汽油。在整个实验过程中,外界环境温度保持在19~20℃波动。
1.2 实验结果与分析
图2为不同的侧开缝宽度下,自通道内燃料被点燃后至旋转火焰形成所需用的时间ts。

图2 不同开缝宽度下旋转火焰的开始时间和燃料燃尽时间Fig.2 Begin time and burning time with different gap widths
由图2可以看出,在开缝宽度为0.3~0.7 m时形成旋转火焰的速度最快,而在开缝宽度太小和太大时均不利于旋转火焰的形成。图2中同时给出了在不同侧开缝宽度下,等量液体燃料被燃尽所需时间tb,可以看出,在侧开缝宽度d接近0.5 m时所需的燃烧时间最少,这说明此时燃料的燃烧速率最高,也间接说明此时火焰的旋转程度相对最为剧烈。
2 单侧开缝竖直通道热流场数值模拟
2.1 模型构建
火灾产生的流场属于多组分、有粘、浮力驱动的弱可压流动。适用于这种流体的模型方程组及基于大涡模拟技术的计算方法在文献[6-7]中有详细推导,在此不再详述,仅介绍计算过程中的相关边界条件参数和网格设置。
根据实验所用燃料热值、在形成旋转火焰时的燃速、实验环境以及实验通道所用材料属性情况,在数值模拟中,设置火源单位面积的热释放率为2 500 kW;白铁皮边界参数设置为:密度 7.8×103kg/m3、比热1.21 kJ/(kg·K)、导热系数 80 W/(m·K);通道前侧玻璃边界参数设置为:密度2 700 kg/m3、比热0.84 kJ/(kg·K)、导热系数0.76 W/(m·K);初始环境温度设置为20℃,压强为1个大气压;假设壁面无滑移,壁面的导热按一维导热处理。
数值模拟的网格选择根据无量纲表达式D*/δl来确定,其中D*为火焰特征直径,δl为网格尺寸,D*/δl可视为跨越火焰特征直径的网格个数,同时,D*/δl值在 4~16 时可得到有效的结果[8]。D*的表达式为

式中,为火源热释放率,ρ∞为环境空气密度,CP为环境空气比热,T∞为环境空气温度。根据实验条件,计算可得D*=0.68 m。若要能捕捉到火羽流的信息,特征直径至少覆盖10个网格[9],则要求网格尺寸约为0.068 m。在平衡计算机性能和计算所需时间的基础上,选取立方体网格尺寸为0.05 m,从而有D*/δl=13.6,在可取得有效结果范围之内。
2.2 数学模型有效性验证
在竖直通道侧开缝宽度d为0.7 m时,流场的扰动较大,稳定性较差,此时流场准确模拟的难度最大。取热流场达到稳定状态时中心轴线上各高度测点处30 s的温度实验测量数据和数值模拟结果,并采用Euclidean函数分析方法[10]计算实验测量值和数值模拟结果之间的模与余弦值,以对两者进行定量对比分析,结果如图3所示。由图中可以看出,温度实验测量值和模拟值在通道上部符合的较好,而在通道底部火源附近偏差稍大。这是由于在实验过程中,火源处发生复杂的化学反应,并且热释放率的值不稳定的原因。鉴于旋转火焰热流场的复杂性,尽管数值模拟结果与实验结果在个别位置处存在一定的偏差,但从总体来讲,偏差均在可接受范围内,而且,模拟结果足以表现出与实验结果一致的热流场分布规律,表明所采用的数学模型以及对相关边界条件的设置在一定程度上可以预测该竖直通道内的热流场。

图3 温度的实验测量值与数值模拟结果对比Fig.3 Temperature comparison between experimental and numerical results
2.3 不均匀开缝宽度的数值模拟
将4~9 m高度处的侧开缝宽度保持为0.15 m,只改变4 m高度以下侧开缝宽度,如图4所示。通道侧开缝上部被固定后,相当于通道侧开缝宽度在4 m高度以上有个收缩,根据实验结果,可以确定在本实验竖直通道结构与火源环境下,侧开缝宽度d为0.3~0.7 m时所形成的旋转火焰最为剧烈,因此,若将侧开缝下部宽度d为 0.3、0.5、0.7 m 时,侧开缝上侧收缩幅度分别约50%、70%和80%。
上侧开缝宽度限制为0.15 m时,4 m高度以下的侧开缝宽度d分别为 0.3、0.5、0.7 m 时通道内流场流线图如图5所示。由图可见,尽管侧开缝上侧宽度有一定幅度的收缩,通道内仍可以形成旋转流场。
图6给出了过竖直通道的中心截面(Y=0),沿X轴的正方向在X=0.1 m处的上侧开缝受限与侧开缝宽度保持一致时的平均切向速度之差ΔV随高度的变化规律。从图中可以看出,底部区域的速度差ΔV为正,说明上部开缝受限后,底部的切向速度增大;随着高度增加,ΔV逐渐减少,底部开缝宽度d=0.5,0.7 m 时的 ΔV值均降到负值,在侧开缝宽度发生突变的附近高度降到最低值,这说明在上部开缝受限后,会降低开缝宽度发生突变的附近区域切向速度;达到上部开缝宽度为0.15 m区域后,ΔV值逐渐增大,在通道最上部区域,ΔV值接近0。
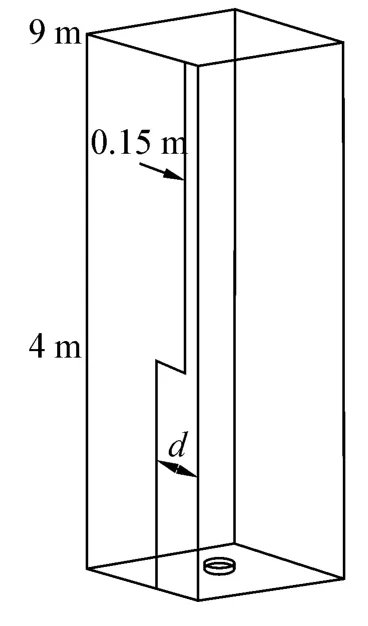
图4 侧开缝宽度不一致的竖直通道示意图Fig.4 Schematic of vertical shaft with inconsistent gap width
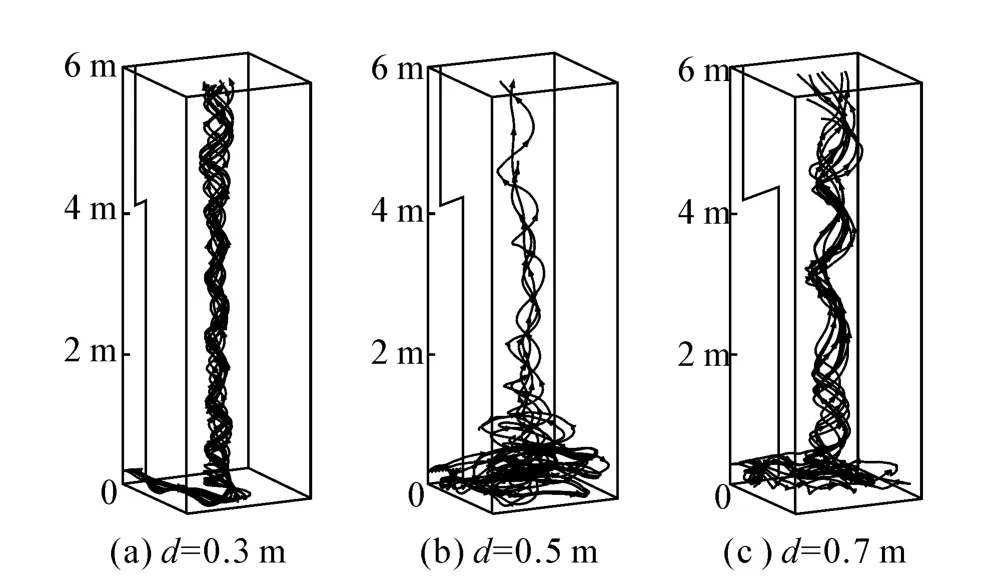
图5 不同开缝宽度的流线图Fig.5 Streamlines at different gap widths

图6 X=0.1 m处的平均切向速度差Fig.6 Average tangential velocity against height at X=0.1 m
若定义无量纲量ζ为流场的同一位置处平均切向速度与平均轴向速度之比,则在不同侧开缝宽度条件下,竖直通道的中截面上X=0.1 m处的ζ随高度的变化规律如图7所示。由图中可以看出,与整个开缝宽度保持一致时相比,在侧开缝上部宽度受限后,ζ值在底部区域变大,在开缝宽度发生变化的4 m高度附近,ζ值降低,在4 m高度以上,ζ值又会有一定程度的升高。由于切向速度是决定旋转力大小的重要参数,而轴向速度主要靠浮力来产生,因此图7结果可以间接说明在4 m高度以上开缝受限后,旋转力与上升浮力之间的关系也受到影响,而限制侧开缝的宽度会增大远离开缝发生突变区域旋转力相对浮力对流场的作用,而在开缝发生突变的附近区域,旋转力较浮力对流场作用程度降低。

图7 X=0.1 m 处的ζ随高度的变化Fig.7 ζ against height at X=0.1 m
图8~10为不同的侧开缝宽度条件下,高度Z=0.8 m的横截面处侧开缝宽度一致和上部宽度受限时的压力等值线图。由图可见,在相同高度处,无论侧开缝宽度是否被限制,均有可形成旋转的良好压力梯度,但旋转中心的位置所有不同。当4 m高度以上侧开缝宽度为0.15 m时,旋转中心向Y轴正方向偏移。

图8 开缝宽度d=0.3 m时Z=0.8 m 的压力等值线图Fig.8 Pressure distribution at Z=0.8 m with d=0.3 m

图9 开缝宽度d=0.5 m时Z=0.8 m 的压力等值线图Fig.9 Pressure distribution at Z=0.8 m with d=0.5 m

图10 开缝宽度d=0.7 m时Z=0.8 m的压力等值线图Fig.10 Pressure distribution at Z=0.8 m with d=0.7 m
图 11~13 分别为d为 0.3、0.5、0.7 m 时,侧开缝受限前后,侧开缝处的U速度等值线分布情况,速度值U为正表示气流由外界流入通道,而速度值U为负表示气流由通道内向外界流出。通过比较后可以看出,侧开缝受限前后结果有类似之处,U速度均在开缝靠近通道前端壁面一侧的流速最大,流速的分布均类似竖条型,并且均在侧开缝的下部流速较大,而且随着高度的增大流速逐渐减小。不同的是,通道上部开缝受限后,在通道4 m高度以下相同位置处的流速较通道开缝上下一致时稍高,并且在靠近前端壁面一侧处,流进通道的流速不再随着开口宽度的增加而减小,而是随着开缝宽度的增加而增加。另外,通道上部开缝受限后,由开缝处流出通道虽然仍主要发生在开缝顶端靠近前端壁面一侧,但中性面的倾斜角度减少,近似水平,而且高度比开缝宽度一致时较低,并且中性面高度随着4 m高度以下侧开缝宽度的增加而降低。
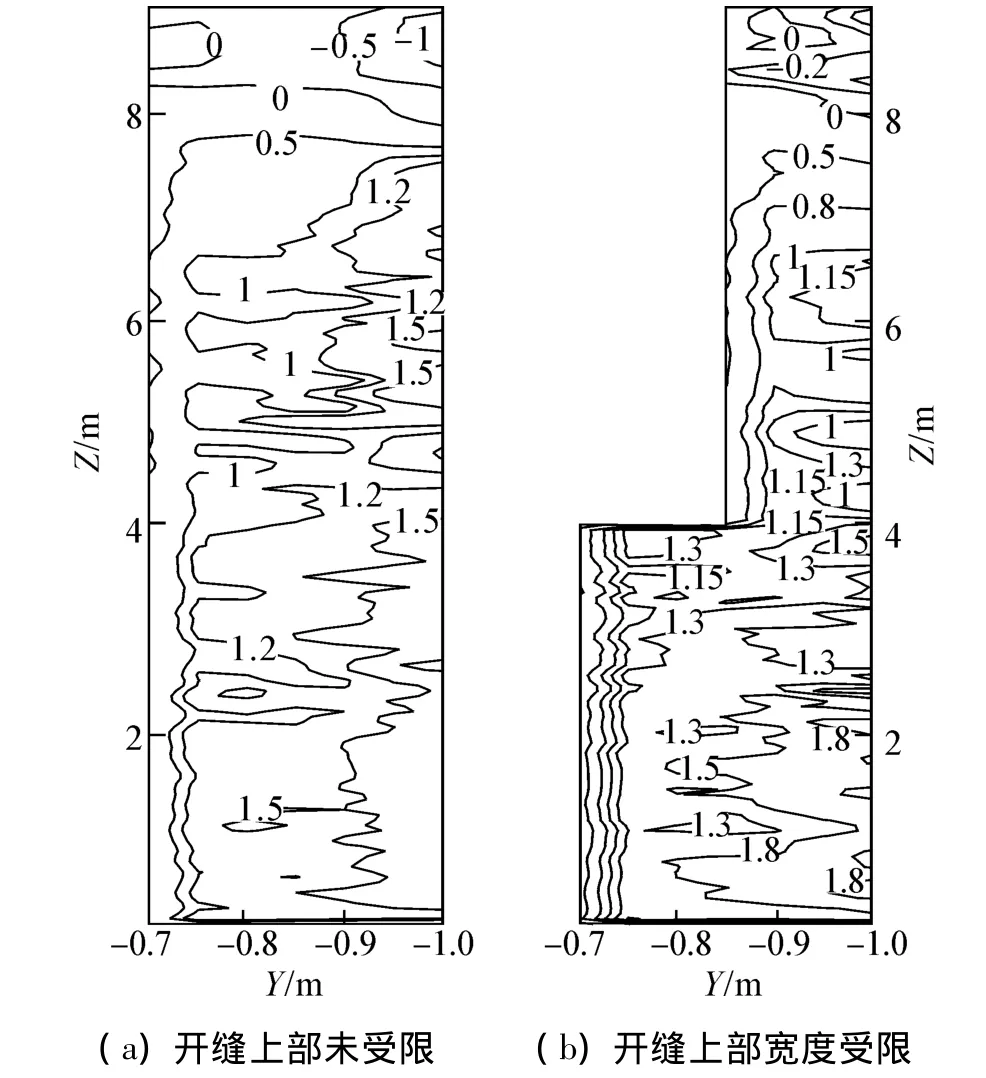
图11 d=0.3 m时侧开缝处的U速度等值线图(单位:m·s-1)Fig.11 U-velocity distribution at corner gap(unit:m·s-1)

图12 d=0.5 m时侧开缝处的U速度等值线图(单位:m·s-1)Fig.12 U-velocity distribution at corner gap(unit:m·s-1)

图13 d=0.7 m时侧开缝处的U速度等值线图(单位:m·s-1)Fig.13 U-velocity distribution at corner gap(unit:m·s-1)
3 结论
根据实验结果确定的可形成旋转火焰的侧开缝宽度范围和数值模拟方法,对典型开缝宽度条件下的旋转热流场进行了数值模拟,并研究了只改变4 m高度以下开缝宽度并将4~9 m高度侧开缝宽度限制为0.15 m时通道内的热流场,通过对结果进行比较分析得到:
1)侧开缝上部宽度受限后,通道内仍可以形成旋转流场,相比未受限情况,通道底部相同位置处的切向速度会增大,旋转力对流场的作用较浮力增大,并使旋转中心偏移,而在开缝宽度发生突变的高度附近区域切向速度会减小,旋转减弱。
2)侧开缝上部宽度受限后,由开缝处流出通道虽然仍主要发生在开缝顶端靠近前端壁面一侧,但较开缝宽度未受限时的中性面倾斜角度减少至几乎为零,而且中性面高度也降低。
3)侧开缝上部宽度受限后,在靠近前端壁面一侧处,流进通道的流速不再随着开口宽度的增加而降低,而是随着开缝宽度的增加而增加。
[1]CHOW W K,HAN S S.Experimental data on scale modeling studies on internal fire whirls[J].International Journal on Engineering Performance-Based Fire Codes,2011,10(3):63-74.
[2]SNEGIREV A Y,MARSDEN J A,FRANCIS J,et al.Numerical studies and experimental observations of whirling flames[J].International Journal of Heat and Mass Transfer,2004,47(12/13):2523-2539.
[3]CHOW W K,HAN S S.Experimental investigation on onsetting internal fire whirls in a vertical shaft[J].Journal of Fire Sciences,2009,27(6):529-543.
[4]HUO Yan,CHOW W K,GAO Ye.Internal fire whirls induced by pool fire in a vertical shaft[C]//ASME/JSME 2011 8th Thermal Engineering Joint Conference(AJTEC2011).Hawaii,USA,2011:T20034-6.
[5]霍岩,郜冶.双侧对开缝竖直通道内热驱动流运动特性[J].燃烧科学与技术,2013,19(1):54-59.HUO Yan,GAO Ye.Motion characteristics of thermal fluid in a vertical channel with double opposite corner gaps[J].Journal of Combustion Science and Technology,2013,19(1):54-59.
[6]霍岩.有限开口空间热驱动流大涡模拟和实验研究[D].哈尔滨:哈尔滨工程大学,2010:8-15.HUO Yan.Research on thermal fluid in partially open enclosure by large eddy simulation and experiments[D].Harbin:Harbin Engineering University,2010:8-15.
[7]MCGRATTAN K B,HOSTIKKA S,FLOYD J E,et al.Fire dynamics simulator(Version 5),technical reference guide.NIST special publication 1018-5[R].Maryland:National Institute of Standards and Technology,2010:15-58.
[8]MCGRATTAN K B,HOSTIKKA S,FLOYD J E.Fire dynamics simulator(Version 5),user’s guide.NIST special publication 1019-5[R].Maryland:National Institute of Standards and Technology,2010:35.
[9]WANG H Y.Numerical study of under-ventilated fire in medium-scale enclosure[J].Building and Environment,2009,6(44):1215-1227.
[10]PEACOCK R D,RENEKE P A,DAVIS W D,et al.Quantifying fire model evaluation using functional analysis[J].Fire Safety Journal,1999,33:167-184.

