多点后方交会及基准点稳定性分析

孙泽信，庞逸群，陈小浩，刘 宁

(1.江苏省交通规划设计院股份有限公司，江苏 南京 211100；2.南京地铁资源开发有限公司，江苏 南京 211005)

多点后方交会及基准点稳定性分析

孙泽信1，庞逸群2，陈小浩1，刘 宁1

(1.江苏省交通规划设计院股份有限公司，江苏 南京 211100；2.南京地铁资源开发有限公司，江苏 南京 211005)

利用间接平差法推导多点后方交会待定点坐标及其精度评定模型，并采用后验方差卡方检验法及针对残差t检验法对基准点的稳定性进行分析，可以较为快速识别不稳定基准点，从而提高多基点后方交会的设站精度。工程应用实例表明，方法在实际工程中具有较高的应用价值。

多点后方交会；后验方差卡方检验法；t检验法；基准点；稳定性

随着城市轨道交通的不断发展，运营期地铁线路越来越多，在给人们生活带来便利的同时也大大促进了地铁沿线及周边的开发，势必会造成运营期地铁隧道局部水平变形[1-3]。为了保证地铁结构的运营安全，必须对其水平位移进行监测。针对地铁隧道这一狭长空间常规平面控制网布设已不能满足监测的时效性及精度要求，极坐标法后方交会设站法具有更为明显的优势[4-5]，而在狭长的隧道内，采用两点或三点后方交会设站精度无法满足监测精度要求，必须采用多点进行后方交会以提高设站及监测精度，为此，采用间接平差法对多点后方交会法求待定点坐标计算及精度评定模型进行推导。

后方交会基准点的稳定性影响后方交会设站精度及监测精度[6-8]，通过采用后验方差卡方检验法及针对残差的t检验法可以较为准确快速地检验基准点的稳定性，提高后方交会设站精度及时效性。

1 多点后方交会模型推导

1.1 函数模型

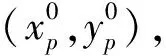
图1 多点后方交会观测示意图

上述误差方程可以写成矩阵形式

V=B·δx-l.

(2)

其中：

计算B,L矩阵时，ρ″=206 265，边长单位为mm，δx单位为mm。

1.2 观测值权矩阵确定

1.3 待定点坐标确定及精度评定

由误差方程及观测值权阵列出法方程并解算得到未知数

δx=(BTPB)-1BTPL,

(3)

则待定点坐标为

(4)

单位权中误差估值为

（2）在保证车辆时刻有电的前提下，便需要根据用户的实际需求，平衡充电费用与出行时间之间的优先程度，达到“既节省时间又比较便宜”的模糊需求。

(5)

式中:f为自由度。

待定点P点坐标改正数的协因数阵为

(6)

则待定点点位中误差为

(7)

2 基准点稳定性检验

根据上述推导的多点后方交会待定点坐标的计算值受基准点坐标影响较大，如果后方交会基准点存在不稳定点，势必影响待定点坐标精度，进而影响监测精度[13]。采用后验方差卡方检验法可以较为快速地判定基准网是否稳定，存在不稳定基准点的情况下，采用基于观测值修正值即残差的t检验法可以准确地检验出不稳定点。

后验方差检验法通过对后验单位权中误差构成统计量，进行χ2检验，当统计量大于给出的分位值时，表明基准网不稳定[14-15]，在此情况下，通过对残差构造t统计量即对边长观测值修正值进行t检验，当统计量大于给定的分位值时，表明该残差对应的基准点不稳定，剔除该基准点后重新进行平差，重新平差后再进行基准网稳定性判断。

1)后验方差检验。

χ2检验的原假设和备选假设为

2)t检验。

t检验的原假设和备选假设：

构造统计量t～t(n-1),i=1…n，统计量自由度为n-1，服从近似正态分布[16]，α=0.01，当t>t0.01，n-1时，表明备选假设成立，该残差对应的基准点为不稳定点。

3 工程应用实例

以某地铁隧道运营期水平位移监测为例，该监测项目采用7个基准点(H1～H7)作为后方交会点。观测仪器采用Leica TM30型全站仪进行观测，仪器标称精度±0.5″，±(0.6+10-6·D)mm，相关平差由采用上述方法自主开发的程序完成计算。各基准点起算数据如表1所示，后方交会观测值成果如表2所示。

根据已推导的多点后方交会计算公式对观测值进行平差，具体平差成果如表3所示;基准网稳定性分析如表4所示。

从表4可知基准网中存在不稳定基准点，需进行基准点稳定性检验，具体如表5所示。

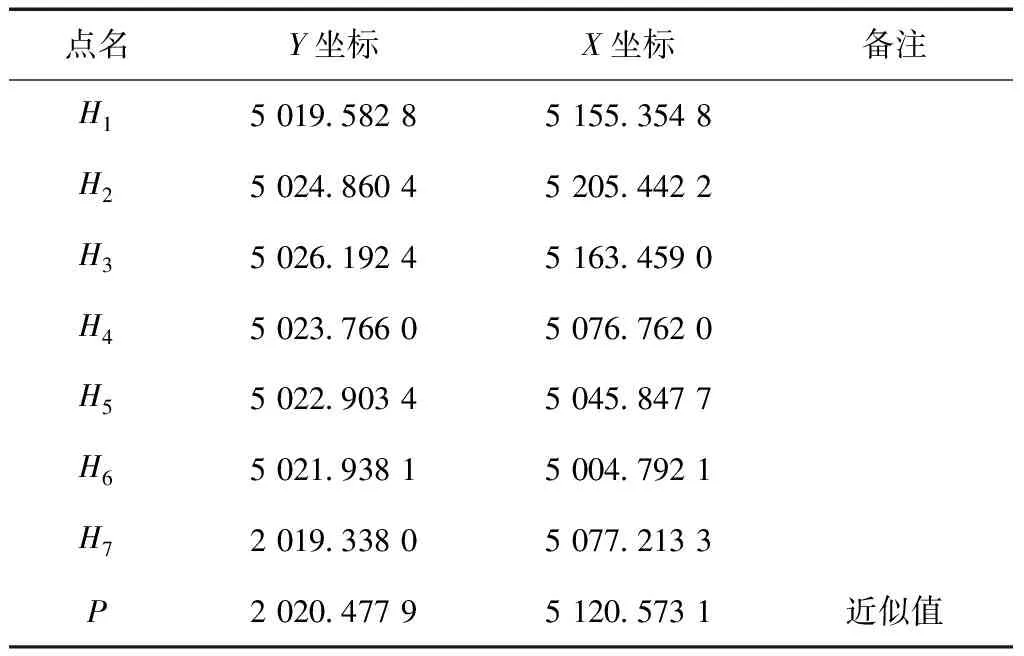
表1 基准点起算数据 m

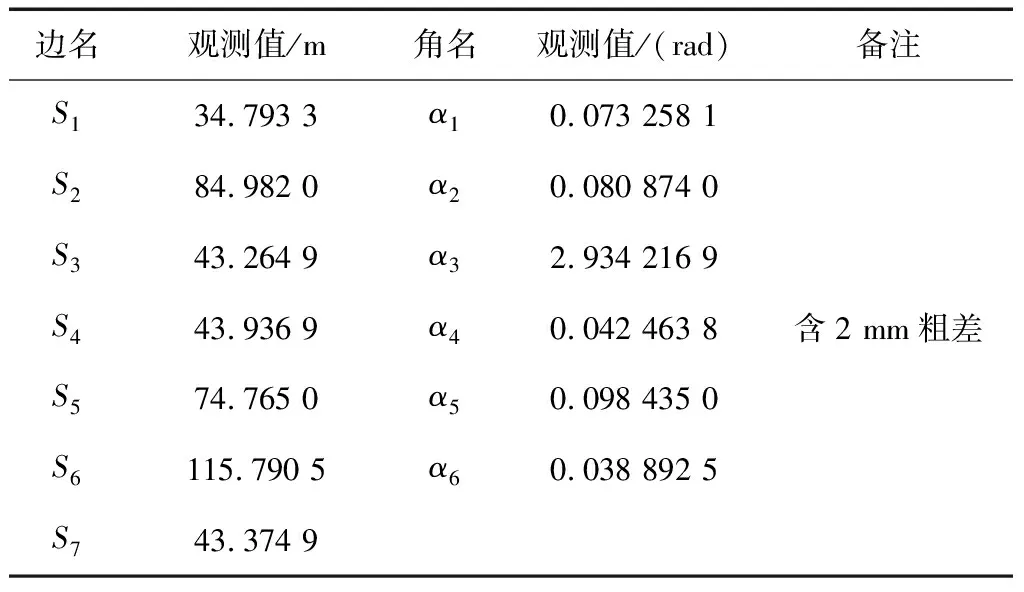
表2 后方交会观测值成果

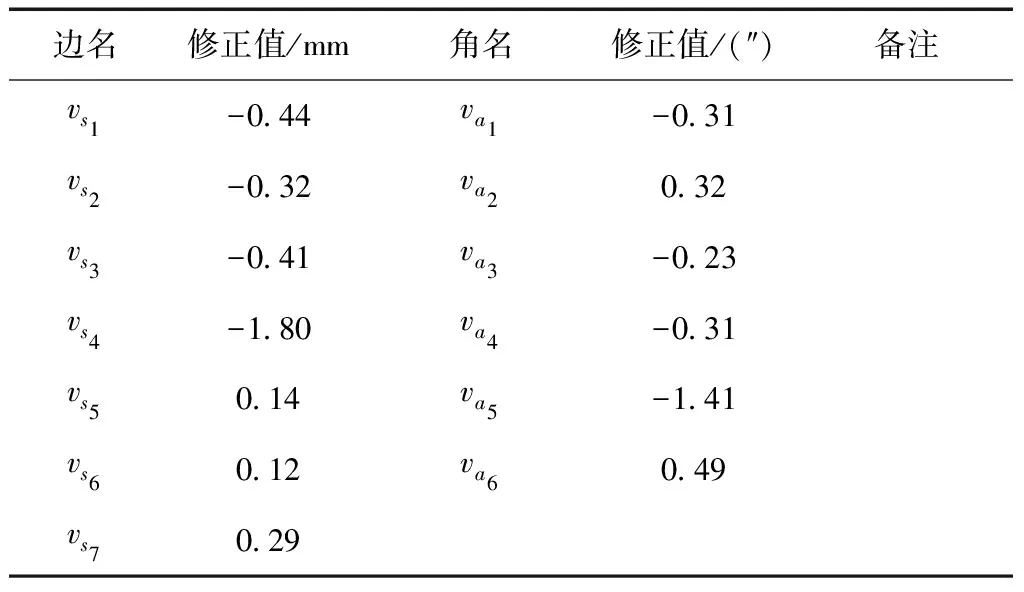
表3 平差成果表

注：δx=0.40 mm,δy=0.08 mm

点位精度MxP=±0.25 mm,MyP=±0.10 mm

待定点点位中误差MP=±0.27 mm

表4 基准网稳定性分析成果

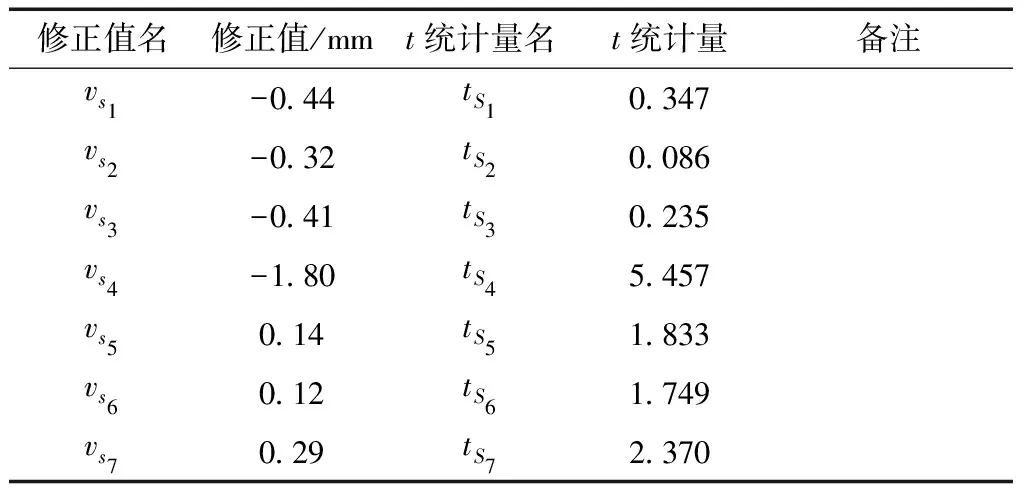
表5 基准点稳定性检验表

注：取α=0.01，t0.01,6=3.143

所有残差的t统计量中，仅有ts4>t0.01,6，故残差vs4对应的基准点H4为显著不稳定点。后方交会平差中剔除该点。

从表5中可以看出,在所有后方交会所用基准点中，仅有H4为不稳定点，剔除该点后重新进行后方交会平差，并再次判断基准网的稳定性。平差结果如表6所示，基准网稳定性分析如表7所示。

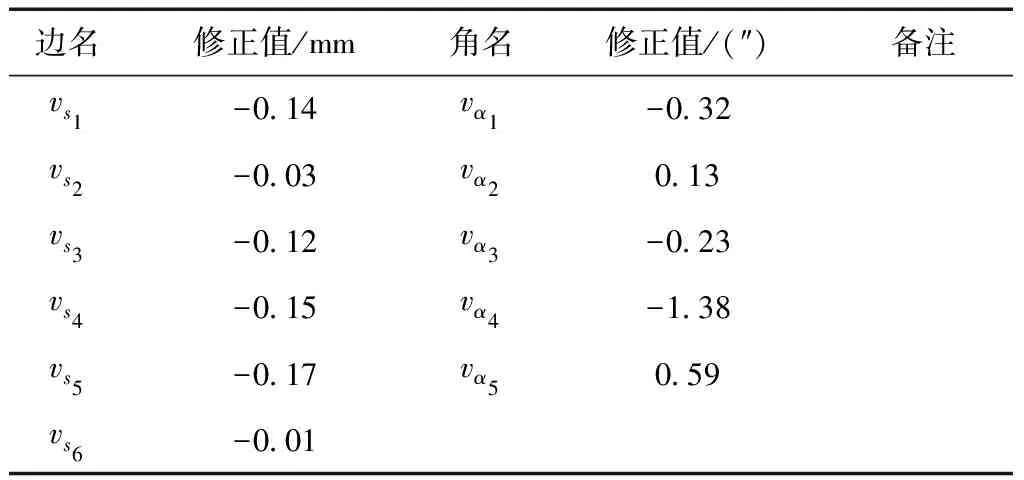
表6 剔除不稳定点后平差成果表

注：δx=0.10 mm,δy=0.10 mm

点位精度MxP=±0.15 mm,MyP=±0.06 mm

待定点点位中误差MP=±0.15 mm

表7 基准网稳定性分析成果表

从表7中可以看出，在剔除基准点H4后，后方交会平差模型稳定状态良好，不存在显著不稳定点，平差成果可以接受。同时对比不稳定点剔除前后的平差成果表即表3与表6，可以看出剔除不稳定点后，后验单位权中误差明显变小，待定点点位中误差也变小，表明基准点稳定性检验方法具有较高的可靠性。

4 结 论

1)经对某地铁隧道运营期水平位移监测中后方交会设站的实例应用，表明所推导的多点后方交会待定点坐标计算及精度评定模型具有较高的可靠性，满足在狭长隧道内的水平位移监测精度及时效性要求；

2)基于观测值修正值的残差t检验法可以准确地判定基准点的稳定性；

3)本文所开发的程序可以极大地提高后续运营期地铁隧道自动化变形监测实时设站的精度及时效性，具有较高的应用及推广价值。

[1]汲广坤.地铁车站深基坑近距离建筑物保护施工技术及措施[J].隧道建设，2011，31(2)：120-125.

[2]郑立常，卫建东，郑俊峰，等.基坑施工对临近运营地铁隧道影响监测的实践[J].测绘工程，2007，16(2):47-50.

[3]邱冬炜，梁青魁，杨松林.北京地铁隧道结构整体变形监测的研究[J]. 测绘科学，2008，33(2):16-17.

[4]范亚军，黄腾，李东升，等.地铁隧道保护区水平位移监测方法的研究[J].测绘工程，2013，22(3)：21-24.

[5]陈喜凤，黄腾，刘岭，等.组合后验方差检验法在地铁隧道变形监测中的应用研究[J].隧道建设，2013,33(1):27-30.

[6]M LIGAS. Simple Solution to the Three Point Resection Problem [J]. Journal of Surveying Engineering, 2013,139:120-125.

[7]J FONT-LAGUNES, J BATLLE. New Method that Solves the Three-Point Resection Problem Usin g Straight Lines Intersection [J]. Journal of Surveying Engineering, 2009,135:39-45.

[8]DEKOV. A numerical method for solving the horizontal resection problem in surveying [J]. Journal of Geodetic Science, 2012,101:65-67.

[9]朱宝训，刘成龙，杨天宇.后方交会方法及其精度评定问题研究[J].山东交通学院学报，2004,12(3):26-29.

[10]武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M].武汉：武汉大学出版社，2003：38-44.

[11]刘成龙.三点极坐标后方交会原理及其精度分析[J].西南交通大学学报，1995,30(3):251-256.

[13]陈永奇.工程测量学[M].北京：测绘出版社，2004.

[13]李秀海，冯金宇.全自动变形监测系统精度分析[J].交通科技与经济，2008,10(4):68-70.

[14]尹晖，杨睿，陈鹏云.监测网稳定性检验方法与应用[J].武汉理工大学学报，2010, 32(6):861-863.

[15]张正禄，沈飞飞，孔宁，等.地铁隧道变形监测基准网点确定的一种方法[J].测绘科学，2011, 36(4):32-34.

[16]陈希孺. 概率论与数理统计[M]. 合肥：中国科学技术大学出版社，2009：183-197.

[责任编辑：张德福]

Multipoint resection and stability analysis of datum point

SUN Ze-xin1,PANG Yi-qun2,CHEN Xiao-hao1,LIU Ning1

(1.Jiangsu Province Communications Planning and Design Institute Co., Ltd.，Nanjing 211100， China; 2. Nanjing Subway Resources Development Co., Ltd.,Nanjing 210005， China)

The coordinate calculation and accuracy evaluation model of multipoint resection are deduced by use of the indirect adjustment, and variance of unit weight chi-square test andttest for residual are adopted on the stability analysis of datum point, which can identify the instability datum point quickly, thus improving the station accuracy of the multipoint resection, Combined with some engineering example, the result shows that the method has a good value in practical engineering.

multipoint resection; variance of unit weight chi-square test;ttest; datum point; stability

2014-02-19

孙泽信(1983-)，男，工程师.

P207；TU198

：A

：1006-7949(2014)08-0015-04