基于单应矩阵约束的黑白棋盘格角点提取

郭俊喜

(神华巴彦淖尔能源有限责任公司 ，内蒙古 巴彦淖尔 015300)

基于单应矩阵约束的黑白棋盘格角点提取

郭俊喜

(神华巴彦淖尔能源有限责任公司 ，内蒙古 巴彦淖尔 015300)

针对Harris算子提取棋盘格角点存在的问题，提出基于单应矩阵的黑白棋盘格角点提取方法。方法首先通过人机交互确定角点提取范围以及计算单应矩阵；然后根据单应矩阵将物方平面上其他点映射到影像上以确定初始的角点位置；最后以初始点位为基准，根据最小距离法确定最终Harris算子角点提取结果。实验结果表明，文中提出算法能有效提取黑白棋盘格角点。

Harris算子；棋盘格角点；单应矩阵；最小距离

在基于平面模板的摄像机标定中，棋盘格模板由于制作经济简单而被广泛应用于摄像机标定中[1]。其中最常用的标定方法如张正友平面标定法，需要对黑白棋盘格平面模板进行摄影，然后提取影像上棋盘格角点坐标，通过利用已知棋盘格角点的像方坐标和物方坐标，建立物方平面与像平面之间的关系,实现相机标定。因此，棋盘格角点提取精度直接影响相机标定的精度。

现有棋盘格角点提取方法可以归结为两类：一类是基于边缘检测结果[2]，两直线交叉提取角点；另一类是直接利用角点提取算子提取棋盘格角点[3-9]。前者依赖于边缘检测结果，同时当影像畸变较大时会发生棋盘格边缘成像弯曲，检测结果会产生较大误差。后者角点检测法是发现影像上灰度变化较大的点，常用的有Harris算子角点检测法和Susan算子角点检测法等，该类算法原理简单，易于实现。但现有角点检测方法存在两个方面问题：一是非棋盘格角点被检测;二是棋盘格角点处提取到多个特征点。针对现有问题，本文提出利用单应矩阵约束Harris算子角点提取结果，首先利用单应矩阵确定初始候选点位置，然后对Harris算子提取特征点，利用初选点根据最小距离法确定最终棋盘格角点。

1 基于单应矩阵约束的棋盘格角点提取

基于单应矩阵约束的棋盘格角点提取方法首先通过人机交互量取4个棋盘格角点确定角点提取范围，同时利用其计算单应矩阵，通过单应矩阵将棋盘格模板上其他点映射到影像上，确定提取角点初始位置。然后采用Harris算子提取角点，通过二次抛物面拟合提高到子像素级精度。再以角点初始位置为基准，通过最小距离确定最终提取的棋盘格角点。算法整体流程如图1所示。

图1 算法整体流程图

1.1 单应矩阵

单应矩阵是数学领域的一个概念，其满足二维投影转换。通过计算单应矩阵可以确定如图2所示两张影像平面之间的对应关系，也可以确定影像平面与物方平面之间的对应关系，使得其一方特征传递到另一方上。

图2 单应矩阵适用条件

假设同名影像S和I，通过S和I之间的N对对应点，就可以确定它们之间的单应矩阵H(其中N≥4)。令(xi,yi)∈I、(xi′,yi′)∈S为一对同名像点，i=1,2,…N。根据同名影像之间的对应关系，每一对同名像点可以得到两个线性方程：

(0,0,0,-xi,-yi,-1,xiyi′,yiyi′,yi′)h=0，

(1)

(xi,yi,1,0,0,0,-xixi′,-yixi′,-xi′)h=0.

(2)

其中：h是矩阵H的向量形式，

h=(h0,h1,h2,h3,h4,h5,h6,h7,h8)T，

(3)

因此可以得到2N个关于参数h0，h1，h2，h3，h4，h5，h6，h7，h8的方程。写成矩阵形式为

Ah=0.

(4)

其中：

(5)

当N≥4时，可以利用奇异值分解(SVD)法求h。

1.2 Harris算子

1.2.1 Harris算子

Harris算子是C.Harris和J.Stephens在1988年提出的一种基于信号的特征点提取算子。该算子的基本原理是取以目标像素点为中心的一个窗口，计算窗口沿任何方向移动引起的灰度变化，可用自相关函数描述。设以像素点(x,y)为中心的窗口在X,Y方向上分别移动u,v，其灰度变化的数学表达式如下：

Ex,y=∑wx,y(Ix+u,y+v-Ix,y)2.

(6)

式中：Ex,y为窗口内的灰度变化度量；I代表图像灰度；w为高斯平滑函数，其具体的表示形式为

wx,y=e-(x2+y2)/2σ2.

(7)

在角点处，自相关函数会根据图像窗口的偏移发生显著的变化。因此在式(6)中，通过泰勒公式有

Ex,y=∑wx,y(Ix+u,y+v-Ix,y)2=

∑wx,y[u2(Ix)2+v2(Iy)2+2uvIxIy]=

Au2+2Cuv+Bv2.

(8)

将Ex,y写成矩阵形式有

(9)

其中，自相关函数矩阵M为

(10)

式中，⊗为卷积操作，对Ex,y对角化处理得

R.

(11)

式中：R为旋转因子；M矩阵的特征值λ1，λ2代表两个主轴方向的图像表面曲率。如果某一点处的两个曲率值都高，说明在该点的图像灰度自相关函数的两个正交方向上的极值曲率均较大，则认为该点可能是一个特征点。为了简化求取M矩阵特征值，直接计算该点的兴趣值I。

I=Det(M)-k(Trace(M))2=

AB-C2-k(A+B)2.

(12)

其中，k为经验值，一般取0.04。在特征点提取过程中，当I值大于给定的阈值时，该点可认为是候选特征点。

1.2.2 二次曲面拟合法

将Harris算子提取角点提高到子像素级精度。利用一个二元二次多项式逼近角点响应函数R(x,y)，具体表达式如下：

R(x,y)=a0+a1x+a2y+a3x2+a4xy+a5y2.

(13)

式中a0、a1、…、a5为待定系数，对于3×3的拟合窗口有9个方程，可以用最小二乘法求解得到a0、a1、…、a5的值，角点响应函数R(x,y)在拟合曲面的极值点应满足如下条件：

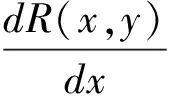
(14)

(15)

式(14)、式(15)两个方程联立求得的亚像素级坐标xx、yy，即

(16)

(17)

1.3 最短距离约束

以单应矩阵映射的每一个点(如图3中红色点所示)为基准，分别判断Harris提取角点(如图3中黑色点所示)到其距离。选取最小距离点作为最终提取的棋盘格角点。该过程可以去掉多余的非棋盘格角点，同时保证每个黑白棋盘格交会处仅提取一个角点。

图3 最小距离示意图

2 实验

在AutoCAD软件中绘制行列分别为16×13大小的黑白相间的棋盘图，其中每小格均为正方形，且边长为16.5 mm。然后用专业的打印机进行打印输出，将输出的棋盘格平整地粘贴在一个平板上。采用尼康D300拍摄影像，大小为4288×2848。

首先通过人机交互方式人工点选角点的提取范围，如图4所示四边框。并根据四个角点坐标计算单应矩阵，根据单应矩阵将提取范围内物方平面上其他点映射到影像上，确定初始特征点位，用来约束后续特征点提取，共180个角点，如图5所示。

图4 人工点选角点提取范围

图5 单应矩阵映射初始点位

采用Harris算子对整张影像进行角点提取，并使其坐标精度达到亚像素级精度。如果不加任何约束，整张影像提取结果叠加显示如图6所示，单独显示如图7所示。除棋盘格角点处提取到角点之外，其他区域也存在特征点，同时，个别角点附近也存在特征点聚类情况。检测角点个数556个。

图6 Harris角点提取结果叠加显示

图7 Harris角点提取结果

利用单应矩阵映射点位约束，根据最小距离判别法最终确定角点提取结果如图8所示：其中十字丝是最终保留的角点，用圆圈加十字丝表示的是已被删除的多余角点，最后保留180个角点，角点提取不包括黑白格网最外围的格网，只提取如图4所示方框内的角点。 其他角点提取结果如图9所示。

图8 单应矩阵约束后角点提取结果及删除的多余角点

图9 其他影像角点提取结果

3 结 论

本文针对采用Harris算子提取角点过程中存在的问题，提出基于单应矩阵约束的黑白棋盘格角点提取方法。实验结果表明，该方法原理简单，计算量小，能准确提取棋盘格角点，为后续基于棋盘格影像的相机标定提供良好的角点。

[1]喻夏琼,高岩,陈向宁.基于非线性优化的摄像机2D标定法[J].测绘工程,2013，22(5):25-28.

[2]蔡振江,王渝,张娟.采用Hough变换和灰度变化的图像角点检测法[J].北京理工大学学报，2005, 25(9):796-799.

[3]张裕,方康玲,刘永祥. 基于Harris算法的黑白棋盘格角点检测[J].计算机应用与软件,2012, 27(8):251-254.

[4]刘阳,王福利,常玉清,等.黑白棋盘格角点检测算法[J].东北大学学报：自然科学版，2007,28(8):1090-1093.

[5]侯建辉,林意.自适应的Harris棋盘格角点检测算法[J].计算机工程与设计，2009,30(20):4741-4801.

[6]刘阳成,朱枫.一种新的棋盘格图像角点检测算法[J].中国图像图形学报，2006,11(5):656-660.

[7]刘嵩,叶玉堂,孙强,等.基于单应性矩阵的棋盘格角点检测研究[J].电子设计工程， 2012, 20(6):114-117.

[8]王剑涛,杨旭波.基于Voronoi图的棋盘格角点匹配算法[J].计算机工程，2010,36(22):280-282.

[9]杨幸芳,黄玉美,李艳,等.基于改进的SUSAN算子的棋盘格亚像素角点检测算法[J].中国机械工程，2010, 21(21):2541-2545.

[责任编辑：张德福]

Chessboard’s corner detection based on homography matrix

GUO Jun-xi

(Shenhua Bayan Naoer Energy Co.,Ltd, Bayan Naoer 015315, China)

Aiming at the problem of chessboard’s corner detection by Harris operator, it proposes one new algorithm of chessboard’s corner detection based on homography matrix. Firstly, this algorithm determines the range of the corner extraction and computes homography matrix by interactive. Secondly, it projects other points from the object plane to the image plane according to the homography matrix for the purpose of determining the initial corner position. Finally, taking the initial point as the reference, the algorithm determines the final Harris operator corner extraction results by the minimum distance method. The experimental results show that, the proposed algorithm can effectively extract chessboard’s corners.

Harris operator; chessboard’s corners; homography matrix; minimum distance method

2014-02-11

郭俊喜(1964-)，男，高级工程师.

TP242;TP391

：A

：1006-7949(2014)08-0036-04