任意两粒子量子纠缠态的概率传送
郭战营,刘应敏,李继武
(焦作师范高等专科学校 物理系,河南 焦作 454003)
0 引言
量子纠缠是两个或多个量子系统之间存在的非定域、非经典的强关联性,利用量子系统的这种特性,Bennett 等人[1]开创性提出了量子态可以隐形传送的思想,根据这一思想,相距很远的两个对象之间通过量子和经典双通道可以传送量子信息,信息在传送过程中被破坏,无法识别,唯有接收者可以还原原始信息.由于这种传送方式的隐蔽性,引起了物理学和通信技术研究领域学者的浓厚兴趣[2].Li 等人研究了怎样通过一个部分纠缠量子态隐形传送一个单粒子态;Lu 等[3]和 Gu 等[4]研究了两粒子态的隐形传送方案;Guo等人[5-6]通过改变量子通道设计了不同的两粒子态概率传送的量子逻辑电路;Zha、Xu 和Dai等人也提出了新颖的量子态隐形传送构想[7].所有这些研究成果都有其独到之处,但是在量子通道的选取以及传态过程的优化方面尚有进一步改进之处.本文为了传送一个任意两粒子纠缠态,选取一个非最大纠缠EPR态和一个部分纠缠GHZ态做量子通道,发送者将贝尔态测量结果通知接收者后,接收者需要对它所拥有的相关粒子做控制非变换,然后对系统做联合幺正变换,就可以实现原始态的概率传送.在使用非最大纠缠态做量子通道时往往需要引入一个辅助粒子来帮助提取系数,从而实现量子态的最后传送,我们的方案并不需要引入辅助粒子,只需要先做一个控制非变换调整量子态的基顺序,再对系统做联合幺正变换,就可以直接恢复原始态.由于我们构建的联合幺正变换对所有三十二种情况都是相同的,又无需引入辅助粒子,这就极大简化了传态过程,提高了传态效率.最后利用基本量子门电路,我们构建了实现任意两粒子量子纠缠态概率传送的量子逻辑电路,这个电路没有对引入辅助粒子的作用,使得形式更简洁,更易于操作.
1 计算分析
构建实现任意两粒子量子纠缠态概率传送的量子逻辑电路,具体的传态过程如下:
假设发送者Alice打算将一个未知的任意两粒子态传送给远处的接收者Bob,这个态可以表示为:
|ψ〉12=x0|00〉+x1|01〉+x2|10〉+x3|11〉
(1)
|ψ〉34=a|00〉+b|11〉
(2)
|ψ〉567=c|000〉+d|111〉
(3)
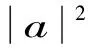
|ψ〉1234567=|ψ〉12⊗|ψ〉34⊗|ψ〉567
(4)
为了实现量子态的隐形传送,发送者 Alice 首先对属于她的粒子 (1,3) 和 (2,5) 分别作贝尔态测量,粒子 4,6 和7的态将坍缩为下列十六种可能的结果之一:
(5)
(6)
(7)
(8)
其中“+” 和 “±” 从左向右分别与粒子(1,3) 和(2,5)的贝尔态相对应,粒子(1,3) 和(2,5)的贝尔态的形式为:
(ij=1,3或2,5)
(9-10)
接下来,发送者Alice通过经典通道将上述测量结果告知接收者Bob,为了重现原始态,Bob需要先对他所拥有的粒子6和7执行控制非变换。在基{|000〉,|010〉,|100〉,|110〉}467下,(5)-(8)式变成如下的形式:
(11)
(12)
(13)
(14)
此时,为了提取系数,Bob不需引入辅助粒子,只需在基
{|000〉,|001〉,|010〉,|011〉,|100〉,|101〉,|110〉,|111〉}467下对其所有的粒子4,6,7做联合幺正变换U1即可,U1的具体形式如下所示:
U1=I⊕R1⊕R2⊕R3
(15)
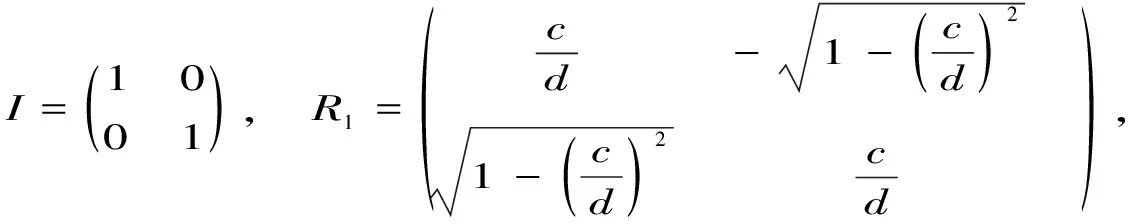
(16)
写成一个完整矩阵的形式为:
(17)
随后,Bob对粒子7做投影测量,如果测量结果为|1〉7,就不会得到需要传送的原始态,传态过程宣告失败;如果测量的结果为|0〉7,为了调整系数的正负,Bob再对另两个粒子4,6做相对幺正变换U2,就能最终实现量子态的隐形传送,U2的具体形式如表1所示:

表1 U2 的具体形式
表中U2的形式中“+”或“-”号的选定取决于对粒子1,3或2,5的贝尔态测量结果。
举一个具体的例子说明如下:
如果Bob获得的贝尔态测量结果为25(〈ψ+|13(〈φ-|,他就对粒子6,7做控制非变换,粒子4,6,7的态将坍缩为:
(18)
在U1的作用,|ψ〉47⊗|0〉a将变为如下形式:
(19)
接下来Bob对辅助粒子7进行测量, 如果测量结果为 |1〉7,就不会得到需要传送的原始态,传态过程宣告失败;如果测量的结果为|0〉7, 粒子4,6的态坍缩为:
(20)
为了调整系数的正负,Bob需要再对上述结果做相对幺正变换U2,针对 方程(20),U2的具体形式为:
U2=(|0〉〈0|+|1〉〈1|)4⊗(|0〉〈1|-|1〉〈0|)6
(21)
方程(20)变为:
(22)
原始态被成功重现,就实现了量子态的隐形传送.
利用基本量子门电路[11],任意两粒子纠缠态的概率传送过程可以用如图1所示的量子逻辑电路来实现:
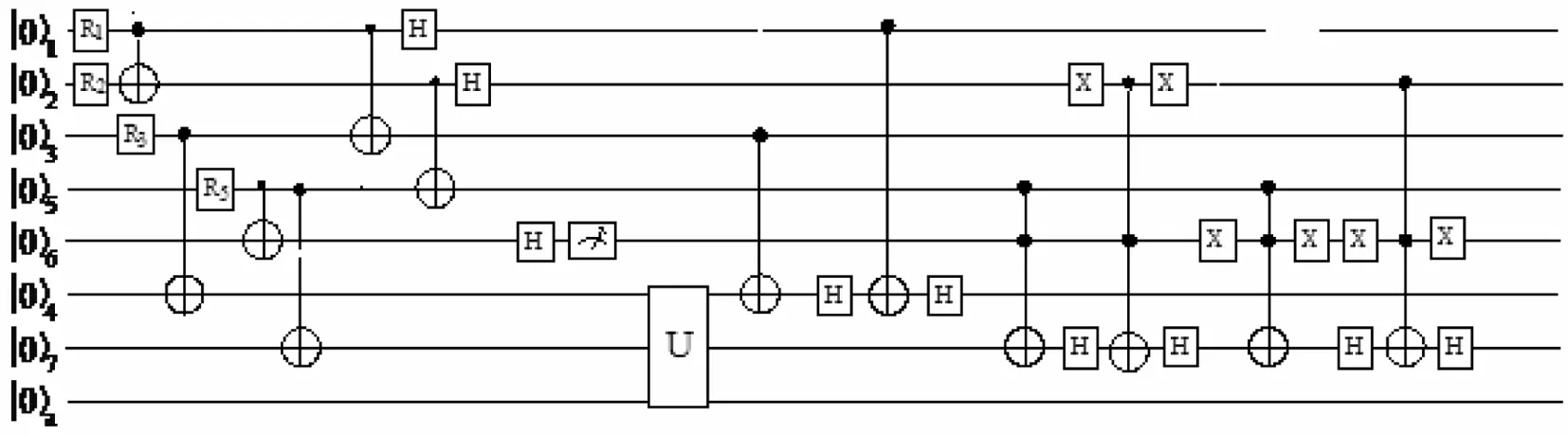
图1 实现任意两粒子纠缠态概率传送的量子逻辑电路

[1]C.H.Bennett, G.Brassard, C.Crepeau, et al.. Teleporting an unknown quantum state via dual classic and Einstein-Podolsky-Rose channels[J]. Phys. Rev. Lett., 1993, 70:1895.
[2]Wan-Li Li , Chuan-Feng Li,and Guang-can Guo. Probabilistic teleportation and entanglement matching[J]. Phys. Rev. A, 2000,61:034301.
[3]Hong Lu and G.C.Guo. Teleportation of a two-particle entangled state via entanglement swapping[J]. Phys. Lett. A, 2000,276: 209-202.
[4]Gu Yong-jian , Zheng Yi-Zhuang, and Guo Guang-can. Probabilistic teleportation of an arbitrary two-particle state [J]. Chin. Phys. Lett, 2001,18(12): 1543-1545.
[5]Guo Zhan-Ying, Fang Jian-Xing, Zhu Shi-Qun,et al. Probabilistic Teleportation of an Arbitrary Two-Particle State and Its Quantum Circuits [J]. Commun. Theor.Phys.2006,45(6):1013-1017.
[6]Guo Zhan-Ying, Shang Xiao-Xing, Fang Jian-Xing,et al.Controlled Teleportation of an Arbitrary Two-Particle State by One EPR Pair and Cluster State[J].Commun. Theor.Phys.2011,56(5):819-823.
[7]X.W. Zha and H.Y. Song.Teleportation Capability of Six-Qubit ClusterState[J] .Commun. Theor. Phys., 2010,54 :1007.

