美国数学与科学课程整合研究进展
袁丽
(江苏理工学院 数理学院,常州 213001)
0 引言
古代或早期的课程是以整体、综合为特征的,其综合是低水平的,是人类认识初级阶段的表现.随着近代自然科学的相对独立和逐渐成熟,分科课程才得以建立并日渐成熟,当代分科课程的理论与实践已达到了相当高的水平.然而,分科课程也日渐显示出学科之间相互隔膜、彼此封闭的弊端,因而,人们希望通过高水平的课程整合,打破各学科之间的界限,建立彼此之间的联系.早在上世纪之交的1901年,美国数学教育家John Perry在一次会议上指出“小学数学教学似乎都将孩子们看作未来的纯数学家”,提出应该重新审视数学和科学课程,更好的协调两者的教学,从而拉开了美国数学与科学教与学整合研究的序幕.自此之后,欧洲也有类似的潮流.到上世纪九十年代,在全球范围课程整合风潮的影响下,有关数学与科学的整合研究更是如雨后春笋大量涌现,甚至在许多国家教育改革文件中强调数学与科学具有的内在相关性,倡导数学与科学课程及教学的协调.了解美国有关数学与科学课程整合的研究,对于实现我国新课程改革所追求的加强课程综合性、促进学科渗透的目标,具有一定的借鉴作用与启发意义.
1 美国数学与科学课程整合的理论研究
1.1 整合的原理
一般而言,分科课程的依据在于客观世界不同领域的相互独立性和特殊性,而课程整合的依据则在于客观世界的整体性和相互联系性.对于“为什么数学与科学课程能够整合”的问题,美国已有研究者亦是从两者具有的内在一致性方面寻求依据.有从学科的视角出发,认为数学与科学具有许多本质联系,使得整合有了可能性和必要性[1].这些联系包括:数学和科学都企图发现客观世界的模式和关系;数学和科学是以相互依赖的方式认识世界的;数学和科学与真实的生活情景相联系,在解决真实问题中需要应用不同的学科知识;数学和科学根本上都需要数量推理.还有研究者从课程的视角出发,探寻两门课程所具有的共同之处,认为共同之处越多,对学生而言更有意义,整合也更有效[2].共同之处包括:两者具有同样的活动,如科学探究和实际问题解决;两者有相同过程和技能,包括分类、测量、观察、收集和组织数据、交流、控制变量、形成模型、估计、试验、作图、推断、数据解释、做出假说、模式认可、预期;两者具有重叠的内容——“Big ideas”,包括平衡、守恒、恒等、测量、模型(包括物理的、数学的),模式(包括趋势、循环、混沌),可能性、反射、折射、度量、对称、系统、变量和矢量.这是因为世界存在着普遍的联系,两个本质上不同的事物,或表面看似无关的内容,却可能内在地包含着某种一致性,这种一致性具有更加抽象的、上位的、原理性的特点,使得毫不相关的事物之间、问题之间、知识之间达到相互的映衬,从而使得知识的整合成为可能.下面一些实例能够说明这种联系.
例:设{ an} 为等差数列, Sn + 1为其前n + 1 项的和,求证:
证设数列{ an}的公差为d,当d = 0 时,由组合数性质知结论成立. 当d > 0 时, a1< a2< …< an + 1,如图1,考虑数轴上坐标为
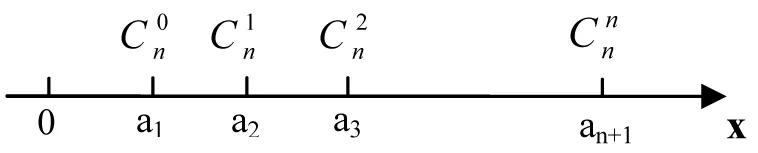
图1 数轴
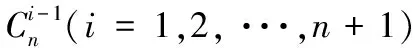
另一方面,根据力学知识,整个质点系对O点的静力矩又等于质点系的重心处集中了整个质点系的质量后关于原点的力矩,即

当d<0时, 仅需改变数轴的正方向而同理可证[3].
又如,新课标北师大版初中数学教材中“等式”的教学设计是让学生通过观察天平的平衡来理解等式的性质;早在两千多年以前,古希腊学者阿基米德曾用力学中物体的平衡原理巧妙地解决了一些几何问题.这些实例都展现了数学和科学间存在联系的实际应用.另外,House指出现代技术使得对实际问题的深入探究成为可能,认为现代技术的应用对数学和科学的整合提出了更多的要求[4].
1.2 整合的意义
一般认为,课程整合对于适应学科日益分化与交融的发展需要、解决现代社会日趋复杂的危机问题、满足学生的发展需要等三方面具有重要意义.关注数学与科学整合的研究者也提出“整合本身不是目标,而是作为成就其他目标的一种手段”[5],他们认为:数学与科学课程的整合,能够使学生获得有关自然世界的数学和科学知识的同时,获得科学和数学的思维习惯[5];强调数学与科学概念间的联系将导致更有意义的学习,能使学生形成深度组织、相互联系丰富的知识结构[4];基于学生个人、社会问题和兴趣的科学和数学的整合经历,可以增强学生的成就动机,并且这方面的经验有助于鼓励、支持和培养学生对自己从事科学和数学的自信心[2];数学与科学课程整合教学能够帮助学生理解知识的价值,为学生提供真正的、多种的理解和认识,改变学生对科学和数学的理解[5].
1.3 整合的模式
关于如何进行整合,即整合的模式,一般有狭义和广义之分.狭义的课程整合是将课程整合视为建构一种新型的课程形态,把具有内在联系的不同学科、不同领域的内容或问题统整为一门新的学科;广义的课程整合通常指“使学习计划中分化出来的各个部分比较紧密地联系起来的专门努力”[6],即把分门别类的课程或学习科目,以及特定的一系列学习活动紧密联结在一起,加强纵向和横向的配合,构成具有整体效应的课程结构[7].然而,美国研究者对数学与科学课程整合模式的理解是因人而异的,用于描述整合的术语也很多,如:联系、协作、协调、相关、交互作用、相互依赖、多学科的,学科间的、跨学科的、统一的,等等,不同术语反映不同的整合程度.综合美国已有研究和实践中多样化的整合模式,可归纳为从一端“独立的数学”到另一端“独立的科学”的整合模型[8],如图1:
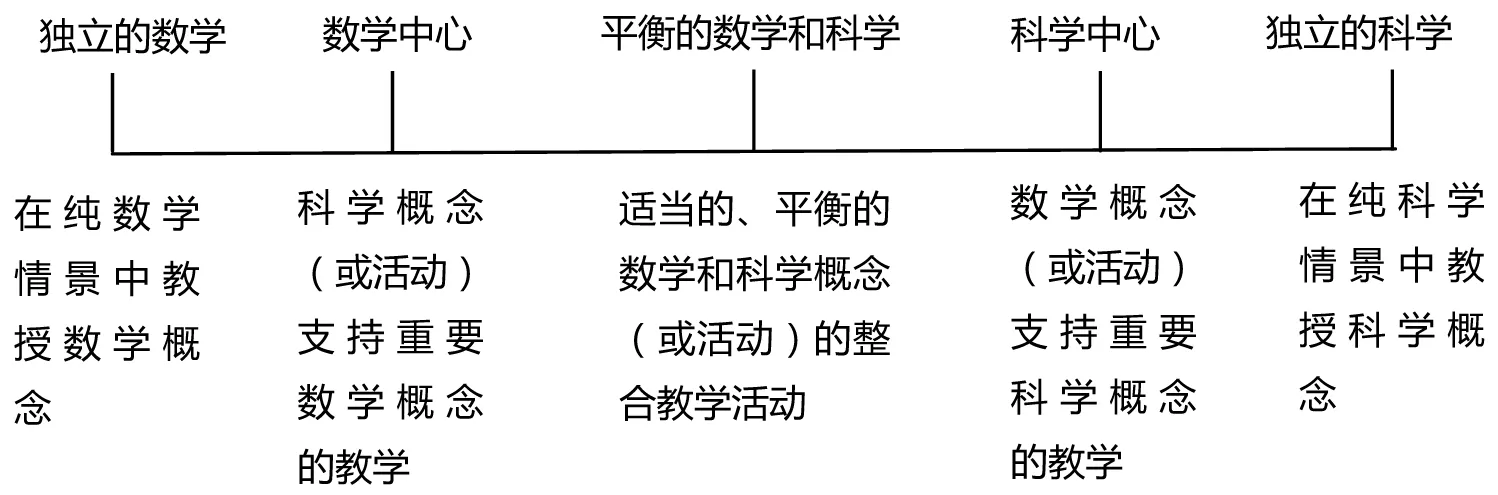
图2 数学和科学概念/活动整合的连续结构图
在这个连续的整合模型结构中,两端“独立的数学”与“独立的科学”为分科的课程形式,两门课程之间几乎没有联系.“科学中心”、“数学中心”是指由一门学科的学习来支持另一门学科的学习,即在学科内部开展与其他学科的整合.有研究者主张“科学中心”和“数学中心”应两者同等并行,也有研究者主张应根据需要交织地进行.居中的“平衡的数学和科学”具有最高整合水平,即狭义的整合模式,有的研究者将其理解为进行“数学概念”与“科学概念”的整合,如特定学科分支的(如代数与科学)、特定内容的整合课程,也有研究者将其理解为问题解决型的整合活动,如基于过程的、方法的、主题的整合项目,以及基于技术的项目或当地社区项目等.
Berlin和White虽没有提出一个合适的整合模型,但是他们提出了一个较为全面的、有价值的整合理论模型[2],该模型指明了进行数学和科学课程整合所需要考虑的六个方面:学习的方式——整合应基于学生是如何经历数学和科学学习的,以及基于学生是如何组织和思考数学和科学的.理解的方式——学生是通过归纳和演绎的方式了解世界的.过程和技能——数学和科学的整合存在于调查、探究、实验和问题解决等过程中.内容知识——数学和科学的整合存在于科学和数学重叠的学习内容中.态度和理解——科学教育与数学教育有许多共享的价值、态度和思维方式,包括:认可科学和数学发展变化的本质、基于数据做出决定和行动、适当的怀疑、求知欲、诚实客观、依赖逻辑推理、愿意思考其他的解释、为达到更好的理解而进行合作学习等.整合应体现孩子们对科学和数学的这些信念.教学策略——科学与数学整合的教学设计应考虑以下标准:合作或者个体进行探究或问题解决的时间、多种形式表达与交流的机、利用实验室设备和其他工具的机会、适当应用科技如计算器和计算机、成功经历的机会、表现性评价.
2 美国数学与科学课程整合的实证研究
2.1 整合的效果研究
美国许多个人和组织积极发展强调科学与数学相互作用的课程材料和项目,其中有明尼苏达数学和科学项目,小学统一科学和数学项目(USMES),学校科学和数学整合课(SSMILES),数学和科学大探索项目(GEMS),整合数学和科学的活动 (AIMS), 芝加哥大学整合数学科学教学项目(TIMS),等等.一些研究者对整合实施效果进行了研究:Elliott等人对应用CBL(微机实验室)和TI(图形计算器)的“数学与物理跨学科动手做”课程进行了调查研究,结果表明,教师教学风格改变了,学生对数学和物理的兴趣增强了[9];还有人研究了大学阶段的科学与代数课程整合的效果,发现对数学和科学的学习是有用的,学生的问题解决能力没有大的提高,批判思维能力有少许的提高,对数学的态度更加积极了[10].Hurley应用元分析的方法研究了31个已有数学与科学课程整合研究的效果,发现整合对学生科学成绩的平均影响效果高于对数学的影响效果,不同的整合形式对学生的数学和科学成绩的影响均有所不同.然而,Hurley研究还发现总体平均影响效果的显著性程度不够高,并分析指出对数学成绩的正影响可能归因于良好的计划和教学,而不是整合课程本身[11].
2.2 影响整合实施的因素研究
对于影响整合实施的因素,美国研究者多认为教师是一个重要因素.一方面研究发现,教师对待整合这个主题的信念和态度与整合的效果及课堂实践是相关的[4],教师的态度是影响整合实施的一个主要因素[12];另一方面,教师自身具备的其他学科知识是影响整合实施的又一个重要因素.因为整合所达到的程度取决于教师是否形成了对学科内容以及学科之间概念联系的坚实理解,取决于教师在解释他们学科领域中的关键概念、原理、原则和理论所使用的例子、数据和来自多种学科和文化的信息[13].一项对职前教师进行的学科整合教育的研究发现,经过培训,教师们对整合的态度和认识没有变化,但是对于整合可行性的认识有了很大的改善[14].另外,也有研究者认为,一些客观因素也是影响整合实施的原因,如整合的外部环境,包括支持性的课程材料的开发、精确评价学生进步的方法、职前和在职教师教育的转变、教育和科学团体、学生和公众普遍的支持和认可等等[15].还有时间因素,有调查显示[15],小学专家教师认为,虽然他们有更多的数学和科学的知识背景,清楚这些领域的课程资源,能够进行数学和科学的整合教学,但由于没有充足的时间,无法进行整合.
3 反思与启示
美国数学与科学课程整合的研究与实践已有百年的历史,然而,实际教学中两门学科更好的协调和相互促进还远未达到.反思美国已有数学与科学课程整合研究可以发现:一方面,虽然研究者认识到数学与科学课程整合的重要性,但还没有从各种理论和实践的观点中形成一个富有建设性的统一的整合思想框架,从始至终都存在一个普遍深入的问题:对于不同的教育者,整合意味着不同的东西.另外,有关研究多是理论分析和经验总结,缺少基于这些理论的实证研究,尤其缺少能够证明整合课程的确优于设计良好的传统课程的实证研究.另一方面,已有研究缺少对数学与科学整合的范围与可能性的探讨.因为任何整合的方法都应该基于对整合所涉及的学科的理解[16].数学研究自然界系统内部具有的数量关系(数)和空间形式(形),自然科学研究物质世界所具有的客观规律(质),因为物质世界是数、形以及质的统一,因而数学与科学才具有一些必然的联系,也才有了整合的可能性.但是,科学和数学又有其各自的独特性,建构一个跨学科的概念要比探索数学(或科学)概念在科学(或数学)的支持下的有效学习艰难的多[17].不仅如此,从学科研究方法上看,科学与数学两者探索知识的途径是截然不同的,科学知识是通过实证的手段经由归纳的途径而获得的,而数学知识是通过逻辑的方法经由演绎的途径获得的,这一点也必然限制了数学与科学整合的范围与可能性.
尽管如此,我们仍能够从中获得有益的启发:
首先,必须坚持数学与科学课程整合的努力方向,坚定SSMA达成的两个共同认识:(1)数学和科学的整合绝不会代替数学和科学,它们是有区别又相关的两门学科;(2)数学和科学的整合,是使学习者面对的是新的数学和新的科学,仅仅孤立的教授数学或科学是应受到冷落的.实际上我国也正在实践着数学与科学的整合:数学课程改革提倡加强数学课程和教学与实际的联系、强调数学建模教学,而综合科学课程及分科科学课程强调科学探究、开展STS教学、设置综合实践活动课程等,这些改革实际上都与数学和科学课程整合旨意相符合.其次,在坚持已有改革与实践的基础上,继续寻求整合的更大发展空间.必须突破数学与科学的表层相关,实现从表层相关到逻辑统整、从工具嬗越到价值体认、从学科素养到人的和谐的整合目标,积极探索各种范围的整合及相应的有效方式,力求多方位、多层次、多方式地开展数学与科学的课程整合.最后,需要加强以整合为目的的教师教育.因为教师是影响数学与科学课程整合实施的关键因素.然而,一般教师的教学准备都是单一学科取向的,缺乏对其他学科知识的理解,从而出现一个严峻的问题:教师如何能够胜任促进学科渗透的任务.要解决这个问题,必须加强以整合为目的的教师教育,提升教师进行跨学科知识整合的能力,才能真正落实数学与科学课程的整合.
[1]House P A.(ED). Science and Mathematics: Partners Then…Partners Now[C]. School Science and Mathematics Association,1990:1-8.
[2]Berlin D F , White A L. The Berlin-White Integrated Science and Mathematics Model[J]. School Science and Mathematics,1994,(1):2-6.
[3]刘继堂.用物理知识解数学问题举例[J].数学通讯,2000,(5):20-21.
[4]House P A. Now More than Ever: The Alliance of Science and Mathematics[J]. School Science and Mathematics,1986,(6):456-460.
[5]Lehman J R. Integrating Science and Mathematics: Perceptions for Preservice and Practicing Elementary Teachers[J]. School Science and Mathematics,1994,(2):58-64.
[6]黄甫全.国外课程整合的发展走势及其启示[J].比较教育研究,1999,(3):38-41.
[7]郭元祥.新课程中课程整合的理念与策略[J].语文建设,2002,(3):4-6.
[8]Lonning R A, DeFranco T C. Integration of Science and Mathematics: A Theoretical Model[J]. School Science and Mathematics,1997,(4):212-216.
[9]Elliott B, Oty K. The Effect of an Interdisciplinary Algebra/science Course on Students' Problem Solving Skills, Critical Thinking Skills and Attitudes towards Mathematics[J]. Int. I. Math. Educ. Sci. Technol. 2001,(6):811-816.
[10]Akihiko Saeki, Akiko Ujiie, Masami Tsukihashi. A Cross-curricular Integrated LearningExperiece in Mathematics and Physics[J]. Community College Journal of Research and Practice, 2001,(25): 417-424.
[11]Hurley, Marlene M . Reviewing Integrated Science and Mathematics: the Search for Evidence and Definitions from New Perspectives[J]. School Science and Mathematics, 2001, ( 5): 259-268.
[12]Stinson K, Harkness S S, Meyer H, Stallworth J. Mathematics and Science Integration: Models and Characterizations [J]. School Science and Mathematics, 2009,(3):153-161.
[13]Banks J. Multicultural Education: Development, Dimensions, and Challenges[J]. PhiDelta Kappan, 1993,75(1):22-28.
[14]Berlin D F, White A L. A Longitudinal Look at Attitudes and Perceptions Related to the Integration of Mathematics, Science, and Technology Education [J].School Science and Mathematics, 2012, (1): 20-30.
[15]Berlin D F.(ED). The Integration of Science and Mathematics Education: Highlights from the NSF/SSMA Wingspread Conference [C]. School Science and Mathematics Association, 1994, (1): 30-39.
[16]Jacobs H H. Interdisciplinary Curriculum: Design and Implementation[M]. Alexandria. VA: Association for Supervision and Curriculum Development,1989:38-41.
[17]Lederman N G, Niess A L. 5 apples + 4 oranges = ? [J]. School Science and Mathematics, 1998,(6): 281-294.

