反应式软件形式化系统研究系统分析

许 明，开金宇，肖 蕾，3

(1.厦门理工学院计算机与信息工程学院，福建厦门361024;2.安阳师范学院计算机与信息工程学院，河南安阳455002;3.上海大学计算机工程与科学学院，上海200027)

形式化系统方法是一种对形式化系统中形式化语言按照计算规则运算的结果依据推理规则进行逻辑推理判断的方法.由三大部分组成.第1部分是形式化语言，由形式化语言的字符集中的字符按照一定的语法规则组成的合法字符串，即是形式化语言，也称合式公式，记为wff.第2部分是形式化系统的推理机制.形式化系统的推理机制由两部分组成，1)公理，不需要依据推理规则即可判断为合法的字符串，称为公理，记作Axioms;2)推理规则，推理规则用于操纵Axioms和(或)其他wffs产生新的合法字符串wffs.第3部分是对形式化系统中形式化语言的语义解释.对形式化语言的语义解释用于对无意义的形式化语言，即合式公式，赋予有意义的领域含义.对形式化语言的语义解释通常采用自然语言，自然语言不是一种完美的形式化语言，但由于其通用性，所以在对语义解释没有严格要求下，使用自然语言对语义进行解释.

形式化系统有两个重要的性质:1)完备性;2)一致性.

假设对于形式化系统F，存在一些形式化语言{f1，f2，f3，…，fn}，对这些形式化语言的解释为{I[f1]，I[f2]，I[f3]，…，I[fn]}.

如果从语义解释的角度出发，存在从序列I[f1]= .T.，I[f2]= .T.，…，I[fk]= .T.可以语义推出I[fn]=.T.的情况下，依据形式化系统的推理规则可以从序列f1，f2，…，fk语法推出 fn，称形式化系统F具有完备性.对完备性的解释为:从一些语义解释为真的合式公式集合能够语义推出某个合式公式语义解释为真，从这些为真的合式公式集合也能语法推出这个合式公式为真.语义推出用符号“|=”表示.语法推出用符号“|－”表示.

形式化系统的一致性表现为:如果从为真的合式公式集合，可以语法推出为真的合式公式，从这些合式公式语义解释为真的集合也可以语义推出这个合式公式的语义解释为真.即对于f1，f2，…，fk|－fn，都有:[f1]=.T.，I[f2]=，T.，…，I[fk]= .T.|=I[fk]=.T.称形式化系统 F 具有一致性.

对于一个形式化系统，通常不严格要求其满足完备性.在使用形式化系统时，通常只考虑其一致性.即语法上可以推理一个合式公式为真，则从语义上，就可以得到这个合式公式为真的语义解释.

形式化方法就是从形式化系统的构建开始的.

1 形式化系统的发展

1.1 形式化系统的原型及发展

命题逻辑推理系统是第一个形式化系统，由命题逻辑语言、推理机制和语义解释三部分组成[1].

由于命题逻辑语言的表达能力非常有限，以命题逻辑推理系统为基础，通过扩大命题逻辑语言的表达能力和增加更多的推理规则，构建了谓词逻辑推理系统.在谓词逻辑推理系统中，形式化语言称为谓词逻辑语言[1].

形式化系统可以用于陈述理论，构建特定理论的形式化系统.

1.2 构建特定理论的形式化系统

理论是对某种现象的事实进行陈述.实际上，各种理论都包含太多的事实，以至于无法明确地一一列举.因此，对理论的陈述常通过基本事实集和特定规律来表达.通过基本事实集和特定规律以及逻辑推理规则可以判断其他的事实现象是否满足该理论.

以谓词逻辑推理系统为基础，引入对特定理论的陈述，就可以构建特定理论的形式化系统，作为支撑的谓词逻辑推理系统的任何性质都自动传承为特定理论形式化系统的性质.

作为特定理论陈述的形式化系统，常常需要将形式化语言约束到仅与特定理论相关的术语集合中，这个集合就构成了特定理论形式化语言的字符集.

特定理论的基本事实集和特定规律构成了特定理论形式化系统推理机制中的公理部分和推理规则，通过作为公理的基本事实集和作为推理规则的特定规律及谓词逻辑推理规则，就可以判断出其他事实现象是否满足该理论.

通常，还需要对特定理论的形式化语言进行语义解释，从而还原到研究者感兴趣的这些现象的某个应用领域.

这样，就构建了一个合适的特定理论的形式化系统.

1.3 更丰富的形式化系统

集合理论、关系理论、函数理论和序列理论等作为通用的数学理论都可以在谓词逻辑推理系统的基础上，通过扩大数学理论形式化语言的字符集，增加构成数学理论形式化语言的语法规则，和增加相应的公理集和推理规则，构建更丰富更强大的数学理论推理形式化系统.

随着形式化系统语言描述能力和逻辑推理能力的增强，可以将其应用到软件工程领域.以通用数理系统为基础，构建软件系统特定理论的形式化系统，将形式化系统理论应用于描述软件系统的某些方面的特定理论.

2 构建软件系统的形式化系统

在一阶数理逻辑语言推理系统的基础上，对软件系统的特定理论构建其形式化系统[2－6].

2.1 软件系统的分类

根据计算机软件系统的系统行为状态变化是否受外力作用，可以把计算机软件系统分为2类:第一类是系统在运行过程中不受外力作用.这类系统的特点是以系统输入为系统初始行为状态，通过完成一个不受外力作用的计算过程，以产生系统输出为系统终止行为状态.这类系统称为变换型系统，记作transformation system.

第二类是系统在运行过程中需要不断地维护系统与外界的交互，从而导致系统行为状态不断发生变化的软件系统.这类系统称为反应型系统，记作reactive system.由于这类系统更强调系统行为状态受外界环境的刺激而导致系统从一个行为状态迁移到另外一个行为状态，而不强调以产生系统输出为目的，因此，这类系统也称为迁移系统，记作transition system.这类计算机软件系统常与硬件相结合，用于对硬件的控制，即嵌入式软件系统，被广泛应用于人类社会的各个领域.因此，从形式化方法去保证这类软件系统的可靠性必将大大增强设计人员对系统设计和实现的信心.

对于变换型系统，系统行为状态只从作为系统输入的初始状态变换到作为系统输出的终止状态，可以看作是迁移系统的特例，因此，作为更一般的计算机软件系统模型，本文将重点介绍迁移系统模型.

2.2 基本迁移系统

以一阶数理逻辑推理系统为基础，构建描述反应式软件系统行为状态变化理论的形式化系统，称为基本迁移系统.基本迁移系统构建如下.

2.2.1 基本迁移系统的形式化语言

1)构成形式化语言的字符集

系统行为状态由构成系统行为状态的原子状态变量按照一阶数理逻辑语言的语法规则组合而成，系统原子状态变量构成了基本迁移系统的形式化语言的字符集，记作vocabulary，简记为V.

V={vi|vi是原子状态变量，i∈0∪N}}.

通常情况下假定系统原子状态变量个数可数;vi可以是数据状态变量，也可以是控制状态变量;数据状态变量根据其取值范围定义其数据类型，可以是布尔类型，整型，列表类型或其他类型;控制状态变量用于表示系统运行过程中进程的位置，因此，控制状态变量的取值范围为系统进程的位置点集合.

此外，出于对状态变量值发生变化进行对比的考虑，我们也把状态变量分为不变状态变量和可变状态变量，不变状态变量的值，在整个系统运行期间的每个状态中都保持不变，而可变状态变量的值，在系统运行期间的每个状态中根据实际运行情况而变化.数据状态变量和控制状态变量都可以是可变状态变量或不变状态变量.

特别需要注意的是，由于在反应式软件中，强调系统行为从前一个状态迁移到下一个状态，因此，我们假定构成系统行为状态的原子状态变量在不同系统行为状态下的取值对应的状态变量名为}也存在于 V 中.

2)基本迁移系统形式化语言的语法规则

基本迁移系统用于描述反应式软件系统行为状态的迁移过程，系统行为状态及迁移是基本迁移系统的形式化语言.

系统行为状态的集合称为系统行为状态域，记作:

Σ ={si|si为系统行为状态，i∈{0∪N}}也称为系统行为状态空间，或简称为系统状态空间或状态空间，通常系统行为状态的个数有限.

系统行为状态由来自基本迁移系统的形式化语言字符集V中的字符，即原子状态变量，按照一阶数理逻辑语言的语法规则构成.

假设系统行为状态sk由原子状态变量按照一定的数理逻辑语言组成语法规则构成，用向量 表示 ，则系统行为状态sk可简记为

使系统初始行为状态s0成立的向量u0的组合项，称为系统行为状态的初始条件，记作Θ.当Θ为真时，对应的语义解释即为系统初始状态s0.

在外力作用下，系统从一个行为状态迁移到下一个行为状态，也可能从同一个行为状态迁移到多个不同的行为状态，这个过程用系统行为状态迁移函数τ表示，简称为迁移函数τ，迁移函数τ是一个从Σ到的映射关系，记作τ:Σ→2Σ.

系统中所有迁移函数的集合用T表示，T={τ|τΣ →2Σ}，简称为迁移集 T.

至此，反应式软件的系统行为状态可迁移情况可以用四元组表示L={V，Σ，Θ，T}来表示.

其中:V表示组成系统行为状态变量的原子状态变量集合;Θ表示使系统初始行为状态为真的原子状态变量组成的条件表达式;Σ表示系统行为状态集合;T表示系统行为状态迁移函数集合.

2.2.2 基本迁移系统形式化语言的语义解释

对形式化语言的语义解释通常采用自然语言.但自然语言受其二义性局限，致使其不是一种完美的语义解释语言，不能在计算机上进行惟一确定性计算，为了更好地使用计算机解释基本迁移系统的某些特性，时序逻辑描述语言成为一种新的选择.具体可参看时序逻辑描述语言的文献资料，本文不再详述.

2.2.3 基本迁移系统的推理机制

基本迁移系统的推理机制，用于推理在外力作用下，系统是否可以从一个行为状态迁移到指定的行为状态.即，给定源系统行为状态和外力序列，是否可以语法推出指定的系统行为状态.

1)基本迁移系统的计算模型

综上可知，系统行为状态可以通过系统原子状态变量依据一定的数理逻辑语言组成规则构成，对外力的描述也可以通过构成外力的原子变量依据一定的数理逻辑语言组成规则构成.对于系统行为状态从sk到sk+1的迁移所受的外力，可以用ρτ(sk，sk+1)来表示，解释为从sk到sk+1的迁移τ所受的外力用ρ来描述或者用ρτ表示.

则:在外力作用下，完成系统行为状态从sk到sk+1的迁移，sk，sk+1∈∑，sk用向量表示，sk+1用向量表示，应满足的条件是:

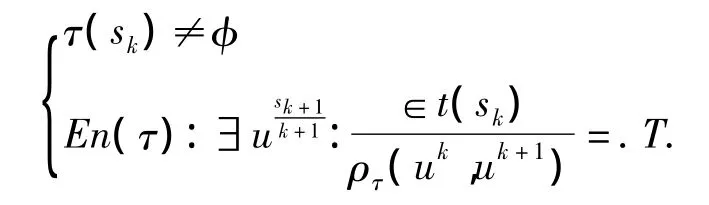
当条件满足时，系统完成从行为状态sk到sk+1的迁移动作，记作Action 1.记完成系统行为状态迁移的动作的集合为Action.在Action 1∈Action的作用下，系统行为状态从sk到sk+1的迁移，记作:sk→sk+1.

记系统行为状态及迁移动作的集合为三元组→，→⊆∑×Action×Σ，则

(sk，Action 1，sk+1)∈→⇔sk→Action 1→sk+1

由此，反应式系统的系统行为状态迁移的计算模型可由三元组T=(V，Σ，→)来表示.

2)基本迁移系统的计算描述

对于反应式系统，其作用是维护系统与外界不断发生的交互，从系统观察者的角度来看，表现为系统行为状态在外力作用下的状态迁移的序列.

设K是任意一个集合，记:

K*表示K中元素的有限序列集合;

表示K中元素的无限序列集合;

K∞表示 K*∪Kω;

序列的连结只需将两个序列并列放在一起即可.

λ代表空序列;

|π|代表序列π的长度.

对于反应式软件L={V，Σ，Θ，T}的计算模型T=(V，Σ ，→)而言，当集合 K= →时，→*，→－ω，→∞，λ，|π|分别代表系统行为状态迁移的有限序列集合，系统行为状态迁移的无限序列集合，系统行为状态迁移的有限与无限序列集合，空的系统行为状态迁移序列，以及系统行为状态迁移序列π的长度.

定义:从s0出发的一条系统行为状态迁移路径，可以用→中的元素的序列表示，记为:ρ=(s0，α1，s1)(s1，α2，s2)…∈→∞.

定义:全路径.如果迁移路径p∈→*，则这条路径是一条全路径，记为a full path.

定义:一次计算.从系统行为状态s，(s∈∑)出发的一次计算，用run=(s，p)表示，p是从 s出发的一条路径.记 first(run)=s，path(run)=p如果p是有限序列，则last(run)为路径p的最后一个状态.

定义:最长计算.对于 run=(s，p)，如果 p∈→*，则称为是从s出发的最长计算，记为a maximal run.

定义:对于两次计算 run1=(s，p1)，run2=(s，p2)如果run1≤run2，则 run称计算 run1恰是计算run2的后缀;如果 run1＜run2，则称计算run1是计算run2的一个后缀.

定义:两次计算的连结，只需将两次计算并列放在一起即可.运行的连结是一个偏序关系.run1run2:run1∈→*∧last(run1)=first(run2)，符号“=”读作定义为.

则对于反应式软件L={V，Σ，Θ，T}的计算模型T=(V，Σ，→)而言，从指定源系统行为状态s0出发在外力作用下，是否可以语法推出指定的系统行为状态sm即:是否存在这样一条路径p=(s0，α1，s1)(s1，α2，s2)…(si，αm，sm)∈→∞，则 last(run(s0，p))=sm.

3)基本迁移系统的推理

由上可知:对于反应式软件L={V，Σ，Θ，T}的计算模型T=(V，Σ，→)而言，从指定源系统行为状态s0出发在外力作用下，是否可以语法推出指定的系统行为状态sm即:是否存在这样一条路径

p=(s0，α1，s1)(s1，α2，σ2)…(si，αm，sm)∈→∞，则 last(run(s0，p))=sm.

证明:当Θ=.T.时，s0为真.

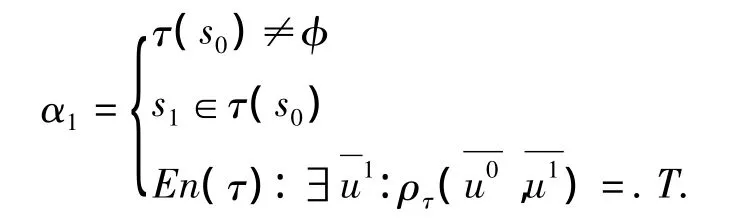
假设α1=.T.则存在 p=(s0，α1，s1)∈→∞ 使得 last(run(s0，p))=s1

依次递推，假设当 sm－1=.T.时，

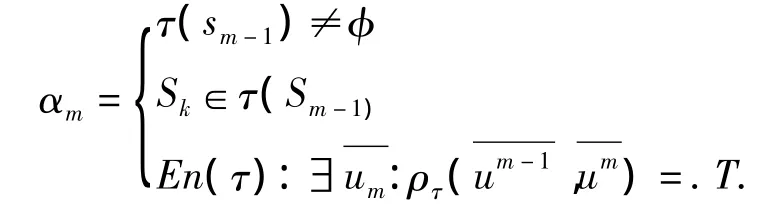
假设αm=.T.则存在 p=(sm－1，αm，sm)∈→∞使得 last(run(sm－1，p))=sm

所以，判断从指定源系统行为状态s0出发在外力作用下，是否可以语法推出指定的系统行为状态sm，转化为判断布尔表达式

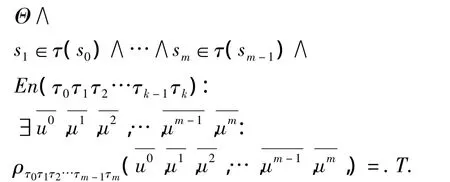
则该问题转换为布尔表达式的可满足性SAT问题.由cook定理可知，布尔表达式的可满足性SAT 问题是 NPC 问题[9].

4)NPC问题的解决方法

对于NPC类问题，由于其是非确定性计算模型下的易验证问题，因此，解决此类问题的技术围绕验证展开，具体可分为两类:ⅰ)公式推理验证方法.依据一阶逻辑语言演算系统的推理规则及反应式系统模型的推理规则，逐步推出系统行为状态序列是否成立的结果.ⅱ)采用算法验证方法，即，常规所说的模型检验(model checking).对于第一类方法，因为在推理过程中，需要专业的参考规则使用技能，因此，这个过程常常需要具有推理规则知识的专家介入，因此，很难将这个方法的使用过程自动化执行.而第二类方法，采用非确定性多项式算法求解的方法，属于暴力遍历验证的方式，虽然方法很粗暴，但却因整个过程可以自动化而受到青睐.

状态爆炸一直是制约这种方法使用的瓶颈，如何解决模型检验方法中的状态爆炸问题一直是模型检验方法的核心问题.

3 扩展迁移系统模型

对于迁移型软件系统，有时还需要对其他方面进行描述，现有的基本迁移系统模型就不完备了，为了弥补这个不完备的鸿沟，需要根据其他需要描述的方面对基本迁移系统模型在描述语言和推理规则上进行补充，以增加系统描述的完备性.

对于迁移软件系统，有时需要刻画其并发特性、实时特性或者混成特性，根据这些特性，分别对基本迁移系统模型进行扩充，得到并发系统[2－5]、实时系统[6－10]和混成系统的系统模型.复杂网络系统是一种新型的系统，用计算机来模拟这类系统的运行规律是对当前计算机软件形式化系统提出的一个新挑战.

4 结语

本文从形式化系统理论出发，介绍了形式化系统的组成和性质，介绍了形式化系统的发展，介绍了形式化系统理论在描述反应式软件系统行为状态变化理论方面的应用，展示了构建反应式软件系统行为状态变化的形式化系统的过程.本文为形式化系统方法在软件系统特定理论描述方面的应用理清了脉络，为描述更广泛的软件系统特定理论及复杂网络系统的描述理清了思路.

[1]JIM W，MARTIN L.Software Engineering Mathematics[M].London:Addison － Wesley Pub(Sd)，1988:271.

[2]AMIR P.Applications of temporal logic to the specification and verification of reactive systems:a survey of current trends[M].New York:Springer－ Verlag New York，1986:510 －584.

[3]AMIR P，ZOHAR M.The Temporal Logic of Reactive and Concurrent Systems:Specification[M].New York:Springer－Verlag New York，1992.

[4]ZOHAR M，AMIR P.Temporal verification of reactive systems.safety.[M].London:Springer－Verlag New York，1995.

[5]NICOLA R D，VAANDRAGER F.Action versus state based logics for transition system [J].Lecture Notes in Computer Science，1990，469:407 －419.

[6]HENZINGER T A，MANNA Z，PNUELI A.Timed Transition Systems[J].Lecture Notes in Computer Science，1992，600:226－251.

[7]MANNA Z，PNUELI A.Models for Reactivity[J].Acta Informatica，1993，30(7):609 －678.

[8]张广泉，沈一栋.混合系统的形式化模型[J].重庆大学学报:自然科学版，1999，22(6):53－57.

[9]王晓东.算法设计与分析[M].北京:清华大学出版社，2008.

[10]刘 阳.基于概率模型检验的服务流程建模与验证[D].上海:上海大学，2012.