左截断右删失数据下二项分布参数多变点的贝叶斯估计

何朝兵，刘华文

(1．安阳师范学院数学与统计学院，安阳455000;2．山东大学数学学院，济南250100)

近年来变点问题成为统计学中比较热门的研究方向，它广泛应用于工业质量控制、水文统计、金融、经济和地震预测等领域．目前变点分析方法主要有极大似然法、最小二乘法、贝叶斯法和非参数方法等．关于变点问题的研究可参看文献［1］-［5］．随着统计计算技术的快速发展，贝叶斯方法的应用越来越广泛，而贝叶斯计算方法中的 Markov chain Monte Carlo(MCMC)方法，使贝叶斯方法在变点分析中的实际操作变得非常方便．二项分布是一类应用广泛的离散型分布，其主要用来描述有限次伯努利试验中“成功”出现的次数，例如，有限个产品中不合格品的个数．关于二项分布的研究可参看文献［6］-［9］．当进行寿命试验时，经常会出现左截断右删失数据，对左截断右删失模型的研究可参看文献［10］-［12］．关于左截断或右删失数据下寿命分布变点问题的研究有一些成果［13-15］，但对数据是既左截断又右删失的情形下寿命分布变点问题的研究还不多见．文献［16］研究了完全数据下单参数指数族分布参数单变点的贝叶斯估计，不同的是，本文主要研究了左截断右删失数据下二项分布参数多变点的贝叶斯估计．首先通过添加数据得到了左截断右删失数据下二项分布的完全数据似然函数，然后研究了变点位置和其他参数的满条件分布，接着利用Gibbs抽样与Metropolis-Hastings算法相结合的MCMC方法得到了参数的Gibbs样本，把Gibbs样本的均值作为各参数的贝叶斯估计，最后的随机模拟试验的结果表明各参数贝叶斯估计的精度较高．

1 离散型分布左截断右删失数据试验模型

设(X，Y，T)是一离散型随机变量，寿命变量X的分布函数为F(x;p)=P(X≤x)，分布律为f(x;p)，这里p是未知参数;Y是一右删失随机变量，分布函数为G(y)，分布律为g(y);T是一左截断随机变量，分布函数为H(t)，分布律为h(t)，且Y，T的分布与参数p无关．假定X，Y，T是相互独立取非负整数的随机变量．对于n个受试样品(产品寿命)，左截断右删失数据的试验模型是，仅在Zi≥Ti时得到观察数据(Zi，Ti，δi)，而在 Zi＜ Ti下无法得到任何观察值，其中

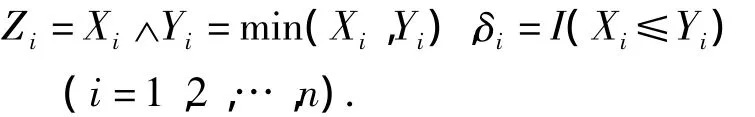
下面求样本的似然函数．

P(无样本观察值)=P(Zi＜Ti)=1-P(Xi≥Ti，Yi≥Ti)=1-其中F=1-F，G=1-G．

为了研究方便，引入示性变量νi=I(min(Xi，Yi)≥Ti)(i=1，2，…，n)．则基于观察数据{(zi，ti，δi):νi=1，1≤i≤n}的似然函数为

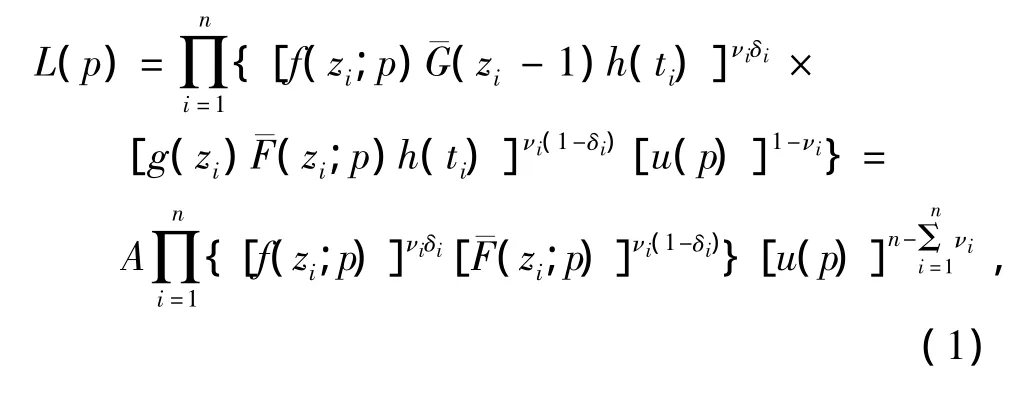
其中A=［h(ti){［¯G(zi-1)］νiδi［g(zi)］νi(1-δi)}，且A与参数p无关．

2 左截断右删失数据下二项分布的完全数据似然函数

若X的分布律为P(X=k)=Ckmpkqm-k(k=0，1，…，m;0＜p＜1，q=1-p)，则称 X 服从参数为 m和p的二项分布，记为X～b(m，p)．

左截断右删失数据试验模型中，假设产品寿命X～b(m，p)，且参数m已知．

由式(1)易知，基于观察数据的似然函数比较复杂，为了方便进行参数估计，下面添加缺损的Xi的值，以获得完全数据的似然函数．具体如下:

当 νi=1，δi=0 时，添加数据 Z1i=Xi=z1i．Z1i的条件分布律为

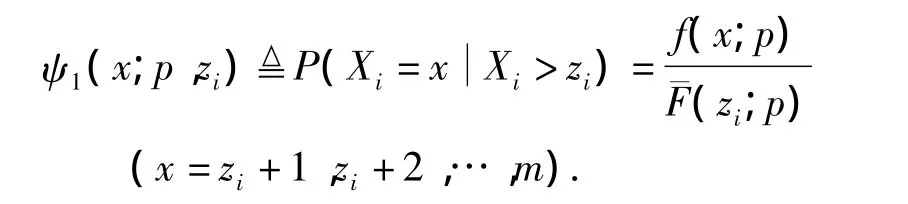
Z1i的条件分布是区间(zi，+∞)上的截断二项分布b(m，p)，其样本可表示为

其中F是b(m，p)的分布函数，F-1为其反函数，U为来自均匀分布U(0，1)的一个随机样本．当进行随机模拟试验编写R程序时，F与F-1可以分别利用函数pbinom和qbinom进行计算．

当 νi=0 时，添加数据 Z2i=Xi=z2i．Z2i的条件分布律为

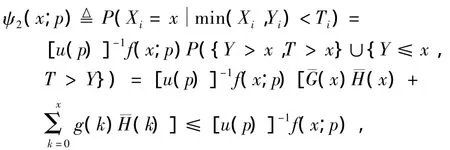
由于f(x;p)是Xi的分布律，且Xi与Z2i有相同的取值，故可以利用筛选法随机产生Z2i的值z2i．其抽样的具体步骤如下:

(1)由均匀分布U(0，1)抽取u，由f(x;p)抽取x．

令z表示zi组成的向量，u1表示 z1i组成的向量，u2表示z2i组成的向量，δ表示δi组成的向量，记ν =(ν1，…，νn)，则完全数据似然函数为

其中s=

3 左截断右删失数据下二项分布参数多变点的贝叶斯估计

二项分布b(m，p)参数p的多变点模型如下:

其中 p1，p2，p3两两不相等，1≤k1＜k2≤n-1．

下面利用贝叶斯方法对变点位置k1、k2及参数p1、p2、p3进行估计．令 D1={1，2，…，k1}，D2={k1+1，…，k2}，D3={k2+1，…，n}．记 θ =(k1，k2，p1，p2，p3)，由式(2)和式(3)可得此变点问题的似然函数为

其中sj=qj=1-pj，j=1，2，3．

下面确定各参数的先验分布．

(1)对于(k1，k2)取无信息先验分布:

(2)对于(p1，p2，p3)取无信息先验分布:π(p1，p2，p3)=1(0 ＜ p1，p2，p3＜1)．

假设(k1，k2)，(p1，p2，p3)相互独立，则

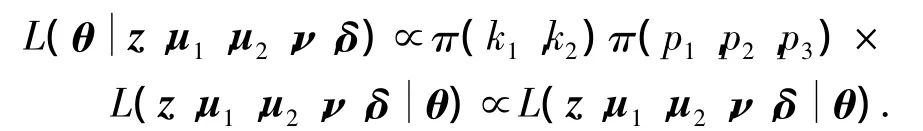
当 νi=1，δi=0 时，

当νi=0时，

其中 z-1i={z1j:j≠i}，z-2i={z2j:j≠i}．

为了书写方便，把满条件分布中的“条件”用

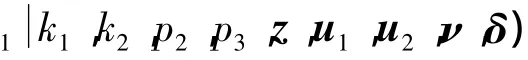
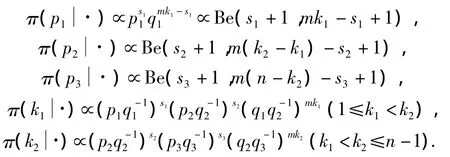
下面利用MCMC方法获得各参数后验分布的平稳分布．z1i利用逆变换法产生，z2i利用筛选法产生，p1、p2、p3的满条件分布是贝塔分布，所以这5个分布都可以直接采用Gibbs抽样;但是k1、k2的满条件分布比较复杂，进行Gibbs抽样比较困难，可以利用Metropolis-Hastings算法进行抽样，此时对于k1和k2选建议分布为离散型均匀分布．

下面写出MCMC方法的具体步骤．

在给出起始点θ(0)=(k(0)1，k(0)2，p(0)1，p(0)2，p(0)3)后，假定第t次迭代开始时的估计值为θ(t-1)，则第t次迭代分为如下几步:

(1)当 νi=1，δi=0 时，由分布 φ1(z1i;θ(t-1)，zi)抽取z(t)1i，令u(t)1表示z(t)1i组成的向量．

(2)当 νi=0 时，由分布 φ2(z2i;θ(t-1))抽取z(t)2i，令u(t)2表示z(t)2i组成的向量．

(3)由 π(p1u2(t)，ν，δ)抽取 p1(t)．

(4)由 π(p2u2(t)，ν，δ)抽取 p2(t)．

(5)由 π(p3ν，δ)抽取 p(t)3．

(6)k(t)1～π(k1，选建议分布q(k(t-1)1，k'1)为取值 1，2，…，k(t-1)2-1的离散型均匀分布，即q(k(t-1)1，k'1)=1/(k(t-1)2-1)，令 α(k(t-1)1，k'1)=}．从 1，2，…，k(t-1)2-1中任意抽取一个k'1，然后产生一个随机数u，若u≤α(k(t-1)1，k'1)，则 k(t)1=k'1，否则 k(t)1=k(t-1)1．

(7)k(t)2～π(k2)，选建议分布q(k(t-1)2，k'2)为取值k1(t)+1，…，n-1的离散型均匀分布，即 q(k2(t-1)，k'2)=1/(n-1-k1(t))，令 α(k2(t-1)，k'2)=min{π(k'2·)，1}．从 k(t)1+1，…，n-1 中任意抽取一个 k'2，然后产生一个随机数 u，若 u≤α(k(t-1)2，k'2)，则 k(t)2=k'2，否则 k(t)2=k(t-1)2．(k(t)1，k2(t)，p1(t)，p2(t)，p3(t))称为Gibbs样本．重复这样的t步迭代M次，便可得到M个独立同分布的5维随机样本．

设(k1(j)，k2(j)，p1(j)，p2(j)，p3(j))(j=1，2，…，B，…，M)为一个容量为M的Gibbs样本，其中B为由于不稳定而舍弃的样本容量，然后利用达到平稳分布的M-B个独立样本的均值作为各参数的贝叶斯估计，即

4 随机模拟

基于上面的讨论，下面进行随机模拟试验．取受试样品的个数n=200，且

假设二项分布的参数m=30是已知的，右删失变量 Yi～b(32，0．5)，左截断变量 Ti～ P(25，0．3)．则参数(k1，k2，p1，p2，p3)的真实值为(40，120，0．2，0．7，0．4)．

根据各个参数的满条件分布使用R软件进行MCMC模拟，主要对变点位置参数k1和k2进行估计分析．在模拟运行过程中，先进行10 000次Gibbs预迭代，以确保抽样的收敛性，然后丢弃最初的预迭代，再进行10 000次Gibbs迭代．迭代从第10 001次开始至第20 000次的R程序的运行结果见表1．

位置参数的Gibbs抽样迭代过程见图1和图2．

表1 参数k1，k2，p1，p2，p3的贝叶斯估计Table 1 Bayesian estimations of parameters k1，k2，p1，p2 and p3

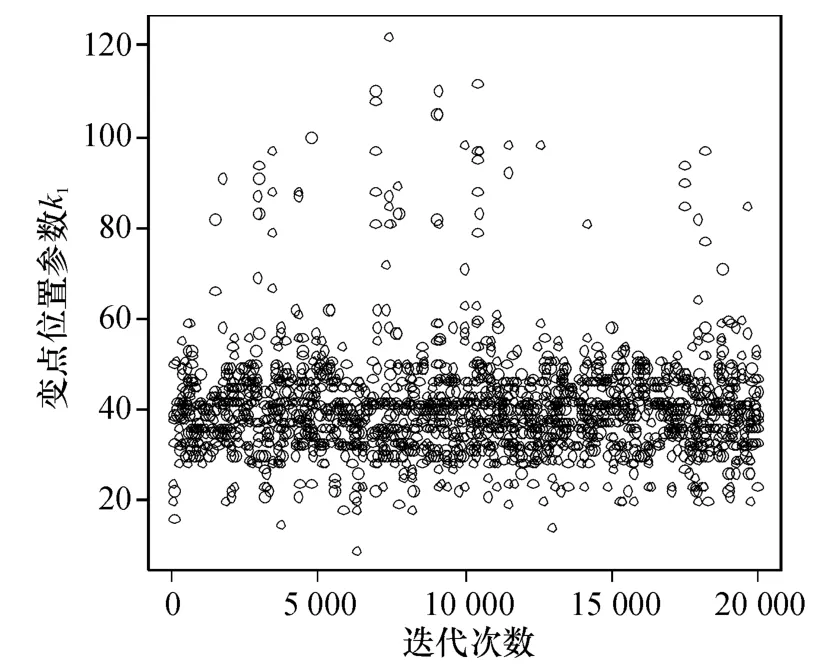
图1 参数k1的Gibbs抽样迭代过程Figure 1 Gibbs sampling iterations of k1

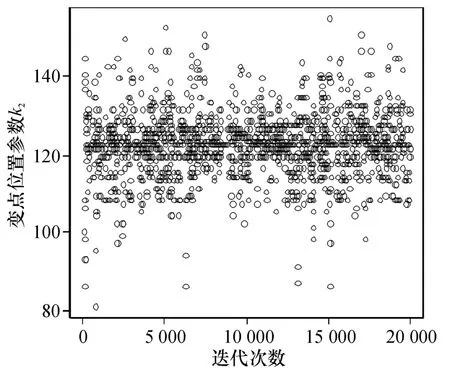
图2 参数k2的Gibbs抽样迭代过程Figure 2 Gibbs sampling iterations of k2

在模型的分析过程中，MCMC的收敛性诊断很重要，模拟时可以对参数进行多层链式迭代分析，即输入多组初始值，形成多层迭代链，当抽样收敛时，迭代图形重合．在模拟过程中，输入2组初始值分别进行10 000次迭代，变点位置参数的多层迭代链轨迹见图3和图4．

最后，对模拟结果进行分析．首先，由表1可以看出位置参数的贝叶斯估计与真值的相对误差不超过2%，其他参数估计的相对误差不超过8%，整体上估计的精度较高，效果较好．其次，要判断所产生的马尔科夫链是否收敛，由图3和图4可以发现，变点位置参数的2条迭代链都趋于重合，收敛性较好．综上分析表明通过MCMC模拟所产生的效果较好．

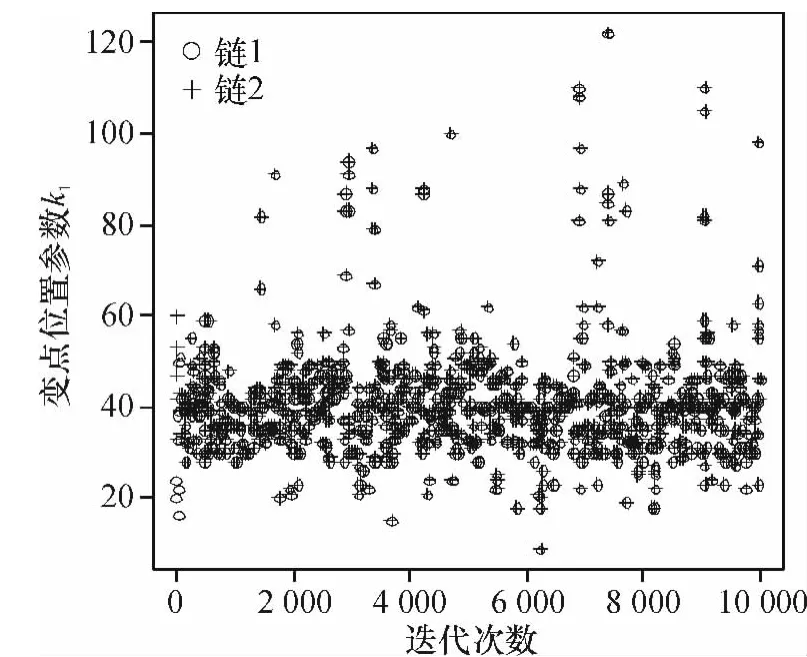
图3 k1的多层迭代链轨迹Figure 3 Multiple iterative chains trace of k1

图4 k2的多层迭代链轨迹Figure 4 Multiple iterative chains trace of k2

［1］Yuan T，Kuo Y．Bayesian analysis of hazard rate，change point，and cost-optimalburn-in time for electronic devices［J］．IEEE Transactions on Reliability，2010，59(1):132-138．

［2］Kim J，Cheon S．Bayesian multiple change-point estimation with annealing stochastic approximation Monte Carlo［J］．Computational Statistics，2010，25(2):215-239．

［3］Fearnhead P．Exact and efficient Bayesian inference for multiple changepoint problems［J］．Statistics and Computing，2006，16(2):203-213．

［4］Andrews D W K．Tests for parameter instability and structural changewith unknown change point［J］．Econometrica，1993，61(4):821-856．

［5］Bai J．Estimation of a change point inmultiple regression models［J］．Review of Economics and Statistics，1997，79(4):551-563．

［6］Koren I，Koren Z，Stepper CH．A unified negative-binomial distribution for yield analysis of defect-tolerant circuits［J］．IEEE Transactions on Computers，1993，42(6):724-734．

［7］Biswas A，Hwang JS．A new bivariate binomial distribution［J］．Statistics ＆ probability letters，2002，60(2):231-240．

［8］Brown L，Li X．Confidence intervals for two sample binomial distribution［J］．Journal of Statistical Planning and Inference，2005，130(1):359-375．

［9］Gupta R C，Tao H．A generalized correlated binomial distribution with application in multiple testing problems［J］．Metrika，2010，71(1):59-77．

［10］Balakrishnan N，Mitra D．Likelihood inference for lognormal data with left truncation and right censoring with an illustration［J］．Journal of Statistical Planning and Inference，2011，141(11):3536-3553．

［11］Cosslett SR．Efficient semiparametric estimation of censored and truncated regressions via a smoothed self-consistency equation［J］．Econometrica，2004，72(4):1277-1293．

［12］Gross ST，Lai T L．Nonparametric estimation and regression analysis with left-truncated and right-censored data［J］．Journal of the American Statistical Association，1996，91(435):1166-1180．

［13］Antoniadis A，Grégoire G．Nonparametric estimation in change point hazard rate models for censored data:A counting process approach［J］．Journal of Nonparametric Statistics，1993，3(2):135-154．

［14］Antoniadis A，Gijbels I，Macgibbon B．Nonparametric estimation for the location of a change-point in an otherwise smooth hazard function under random censoring［J］．Scandinavian Journal of Statistics，2000，27(3):501-519．

［15］Gijbels I，Gürler Ü．Estimation of a change point in a hazard function based on censored data［J］．Lifetime Data Analysis，2003，9(4):395-411．

［16］胡兴．基于贝叶斯方法的单参数指数族分布参数变点的统计推断［D］．乌鲁木齐:新疆大学，2011．Hu X．The statistical inference in parameters of exponential family distribution with change point based on Bayesian method［D］．Urumqi:Xinjiang University，2011．