受噪声影响的复hybrid样本的学习理论关键定理

李俊华, 李海军

(1.河北大学 数学与计算机学院,河北 保定 071002;2.中国地质大学 长城学院,河北 保定 071000)

统计学习理论(SLT)是由Vapnik等[1-2]于20世纪60年代提出的一种针对小样本情况研究统计学习规律的理论, 被认为是处理小样本学习问题的最佳理论. SLT是建立在概率空间上基于实随机样本的, 而概率测度是一个满足可加性的非负集函数, 由于可加性条件非常苛刻, 在现实应用中往往得不到满足, 同时注意到现实中还存在大量的非实(复)随机样本, 因此建立非概率空间上和基于非实随机样本的学习理论就成为了新的研究方向, 许多学者已经开始了该方向的研究并取得了一些重要成果[3-8]. 其次, 对 SLT 的研究多是在较为理想的情况下进行的, 即假设样本不受外界的干扰. 但由于人为、 环境等诸多因素的影响, 这种假设往往得不到满足. 在诸多影响因素中, 研究较多的是噪声[9-10]. 基于上述考虑, 提出并证明了在一类非可加测度空间——机会空间上受噪声影响的复 hybrid 样本的学习理论的关键定理, 为进一步研究机会空间上的 SLT奠定了理论基础.

1 预备知识

定义1[11]设(Θ,P,Cr)是可信性空间，(Ω，A，Pr)是概率空间，则(Θ,P,Cr)×(Ω,A,Pr)称为机会空间.

定义2[11]设(Θ,P,Cr)×(Ω，A，Pr)是机会空间.若Λ⊂Θ×Ω满足：对任意θ∈Θ，都有Λ(θ)∈A，称Λ为一个事件.

定义3[11]设(Θ,P,Cr)×(Ω，A，Pr)是机会空间.事件Λ的机会测度定义为：

性质1[11]设(Θ,P,Cr)×(Ω，A，Pr)是机会空间，则机会测度Ch满足以下性质：

1)Ch{∅}=0，Ch{Θ×Ω}=1；

2)对任意事件Λ，有0≤Ch{Λ}≤1；

3)若事件Λ1⊆Λ2，则Ch{Λ1}≤Ch{Λ2}；

4)对任意事件Λ，有Ch{Λ}+Ch{Λc}=1；

5)对任意事件Λ1和Λ2，有Ch{Λ1∪Λ2}≤Ch{Λ1}+Ch{Λ2}.

定义4[11]设ξ是一个从机会空间(Θ,P,Cr)×(Ω,A,Pr)到实数集R的可测函数，若对任意R上的Borel集B，都有{ξ∈B}={(θ,ω)∈Θ×Ω|ξ(θ,ω)∈B}是一个事件，称ξ是一个hybrid变量.

定义5[11]若对任意R上的Borel集B，hybrid变量ξ和η都满足Ch{ξ∈B}=Ch{η∈B}，称ξ和η是同分布的.

定义6[11]设ξ是一个hybrid变量.若Φ:R→[0,1]满足Φ(x)=Ch{ξ≤x}，称Φ为ξ的机会分布函数.

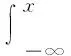
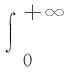
定义9[11]设hybrid变量ξ1和ξ2的机会密度函数分别是φ1(x)和φ2(x)，φ(x,y)是(ξ1,ξ2)的联合密度函数.若对任意x,y∈R，都有φ(x,y)=φ1(x)φ2(y)，称ξ1和ξ2是相互独立的.

性质2[11]设ξ是一个hybrid变量且期望值有限，则对任意实数a和b，有E[aξ+b]=aE[ξ]+b.

定义10[11]设ξ是一个hybrid变量且期望值e有限，则称V[ξ]=E[(ξ-e)2]为ξ的方差.

性质3[11]设ξ是一个hybrid变量且期望值e有限，则对任意实数a和b，有V[aξ+b]=a2V[ξ].

定理1(Chebyshev不等式)[11]设ξ是一个hybrid变量且方差V[ξ]存在，则对任意ε>0，有

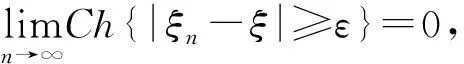
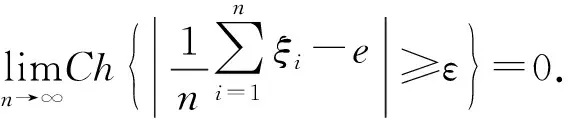
定义12若ξ=α+iβ，其中α,β都是hybrid变量，则称ξ为复hybrid变量.

定义13设ξn=αn+iβn,n=1,2,…，是复hybrid变量序列，若αn和βn，n=1,2,…，都相互独立，称复hybrid变量序列ξn=αn+iβn，n=1，2，…，相互独立.

定义14设ξn=αn+iβn,n=1,2,…，是复hybrid变量序列，若αn，n=1,2,…，同分布，且βn,n=1,2,…，也同分布，称复hybrid变量序列ξn=αn+iβn,n=1,2,…，是同分布的.

定义15设ξ=α+iβ是复hybrid变量，若E[α]和E[β]都存在，称E[ξ]=E[α]+iE[β]为ξ的期望.

性质4设ξ,η是2个复hybrid变量，则对任意复数a和b，有E[aξ+bη]=aE[ξ]+bE[η].

证明设ξ=α+iβ,η=ζ+iγ,a=x1+iy1,b=x2+iy2，则

E[aξ+bη]=E[(x1+iy1)(α+iβ)+(x2+iy2)(ζ+iγ)]=

E[x1α-y1β+x2ζ-y2γ+i(x1β+y1α+x2γ+y2ζ)]=

(x1+iy1)E[ξ]+(x2+iy2)E[η]=aE[ξ]+bE[η].

定义16[12]如果X是一个实(或复)线性空间，对X中的每一个元素x，都有一个非负实数‖x‖与之对应，对应关系满足：

1)‖x‖≥0(∀x∈X),‖x‖=0⟺x=θ(θ是指零元)；

2)‖x+y‖≤‖x‖+‖y‖(∀x,y∈X)；

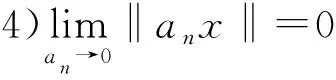
称‖·‖是定义在X上的准范数，X是一个实(或复)的赋准范线性空间.特别当X是实数空间时，假设

‖·‖=|·|.

定义17设ξ是一个复hybrid变量，如果E[‖ξ-E(ξ)‖2]存在，则称E[‖ξ-E(ξ)‖2]为ξ的方差，记为V[ξ].

性质5设ξ是一个复hybrid变量，则对任意复数a和b，有V[aξ+b]=‖a‖2V[ξ].

证明利用性质4即可证明.

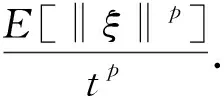
证明假设ξ=α+iβ，Φ(x,y)为(α,β)的联合分布函数[11]，

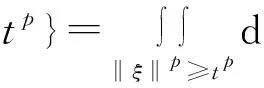
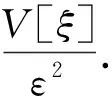
证明在定理3中令p=2即可证明.

急性胰腺炎(AP)恢复期，胰腺外分泌处于低下水平，部分可出现PEI，常见于酒精性AP[4]、重症急性胰腺炎(SAP)和AP伴假性囊肿患者[5]。约1/3的SAP患者可出现PEI，发生率高于轻症AP[6]。随着病情的缓解，AP患者的胰腺外分泌功能可逐渐恢复[7]。

定理5设ξn=αn+iβn，n=1,2,…，是复hybrid变量序列，若{αn}和{βn}分别依机会测度收敛到α和β，则ξn=αn+iβn,n=1,2,…依机会测度收敛到ξ=α+iβ.

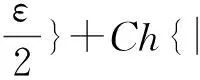
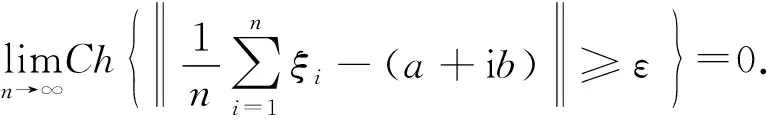
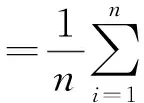
2 主要结论

2.1 复经验风险最小化原则

注1由上述假设和定义19可得

R*(α)=E[Q′(z,α)]=E[Q(z,α)+ξ]=R(α)+e,

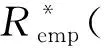
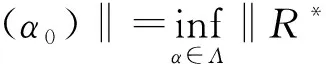
定义21把复期望风险泛函替换为复经验风险泛函，并用使复经验风险泛函最小化的函数Q′(z,αl)逼近使复期望风险泛函最小化的函数Q′(z,α0)，这一原则称作复经验风险最小化原则(CERM原则).

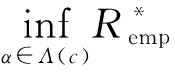
2.2 复hybrid样本的关键定理

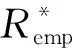
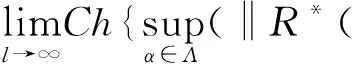
证明必要性：设CERM原则在复函数集Q′(z,α),α∈Λ上是严格一致的.根据严格一致性的定义，对于非空子集Λ(c)={α:‖R*(α)‖≥c},c∈(-∞,+∞),有

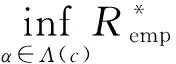
(1)

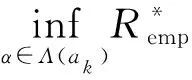
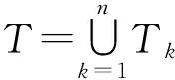
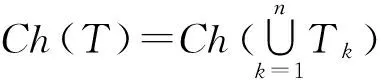
(2)

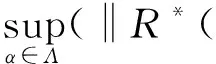
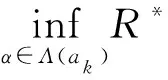
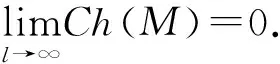
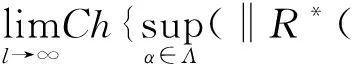
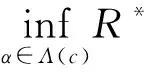
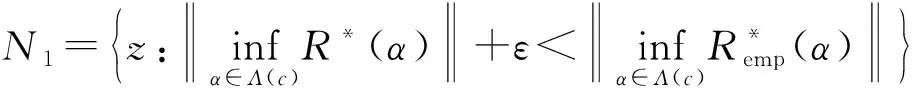
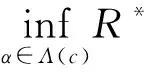
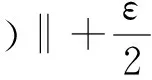
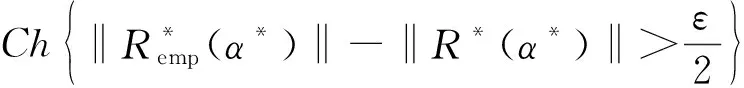
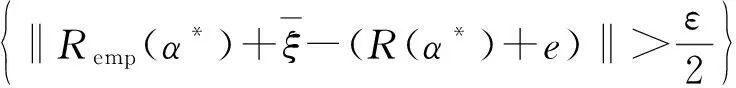
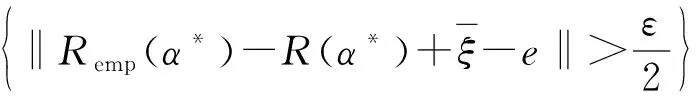
另一方面，假设事件N2发生，则存在函数Q′(z,α**),α**∈Λ(c)使得：

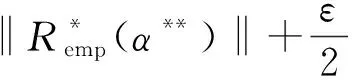
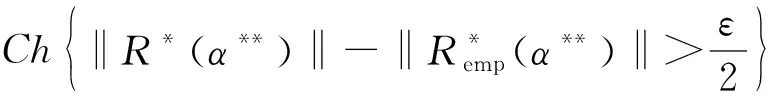
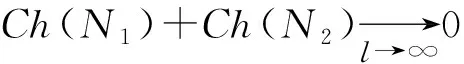
3 结论

考虑到噪声对样本的影响, 在一类非可加测度空间——机会空间上给出了受噪声影响的复hybrid 样本的学习理论的关键定理, 为进一步建立机会空间上的统计学习理论奠定了重要的理论基础.

参 考 文 献:

[1] VAPNIK V N. Statistical learning theory[M]. New York: A Wiley-Interscience Publication, 1998.

[2] VAPNIK V N. An overview of statistical learning theory[J]. IEEE Transactions on Neural Networks, 1999, 10(5):988-999.

[3] 周彩丽, 哈明虎, 鲍俊艳, 等. 基于模糊数的模糊学习理论的关键定理[J].河北大学学报:自然科学版, 2008, 28(5): 449-451.

ZHOU Caili, HA Minghu, BAO Junyan, et al. Key theorem of learning theory based on fuzzy number[J]. Journal of Hebei University:Natural Science Edition, 2008, 28(5): 449-451.

[4] 鲁淑霞, 曹贵恩, 孟洁, 等. 基于取样的潜在支持向量机序列最小优化算法[J].河北大学学报:自然科学版, 2011, 31(2): 113-117.

LU Shuxia, CAO Guien, MENG Jie, et al. A sequential minimal optimization algorithm for the potential support vector machine based on sampling[J]. Journal of Hebei University:Natural Science Edition, 2011, 31(2): 113-117.

[5] 哈明虎, 李颜, 李嘉, 等. Sugeno测度空间上学习理论的关键定理和一致收敛速度的界[J]. 中国科学E辑: 信息科学, 2006, 36(4): 398-410.

HA Minghu, LI Yan, LI Jia, et al. The key theorem and the bounds on the rate of uniform convergence of learning theory on Sugeno measure spaces[J]. Science in China: Series E, Informationg Science, 2006, 36(4): 398-410.

[6] 哈明虎, 冯志芳, 宋士吉, 等. 拟概率空间上学习理论的关键定理和学习过程一致收敛速度的界[J]. 计算机学报, 2008, 31(3): 476-485.

HA Minghu, FENG Zhifang, SONG Shiji, et al. The key theorem and the bounds on the rate of uniform convergence of statistical learning theory on quasi-probability spaces[J]. Chinese Journal of Computers, 2008, 31(3): 476-485.

[7] SUN Xiaojing, WANG Chao, HA Minghu, et al. The key theorem of learning theory based on hybrid variable[Z]. Proceedings of the International Conference on Machine Learning and Cybenetics, Guilin, 2011.

[8] 哈明虎, 王超, 张植明, 等. 不确定统计学习理论[M]. 北京: 科学出版社, 2010.

[9] CHERKASSKY V, MA Y Q. Practical selection of SVM parameters and noise estimation for SVM regression[J]. Neural Networks, 2004, 17 (1): 113-126.

[10] JUMARIE G. Approximate solution for some stochastic differential equations involving both Gaussian and Poissonian white noises[J]. Applied Mathematics Letters, 2003, 16(8): 1171-1177.

[11] LIU Baoding. Uncertainty theory[M].2nd ed.Berlin:Springer-Verlag,2007.

[12] 定光桂. 巴拿赫空间引论[M]. 北京: 科学出版社, 2001.