含二极管非线性介观电路的量子化求解

马金英，阎占元，丁振君

(1. 华北电力大学 数理学院，河北 保定 071003； 2. 河北大学 质量技术监督学院, 河北 保定 071002)

随着微电子技术的发展，集成电路中器件数目一直按照摩尔定律增加.目前，集成芯片中电路和器件的尺度已经趋近于原子的大小，与电子的相干干涉长度接近，通常人们将其称之为介观电路.介观尺度的电路及器件的量子效应凸显，逐渐成为集成技术的瓶颈，在实验和生产实践中，急需建立关于介观电路的量子理论.1973年，Louisell首先讨论了最基本的LC电路在真空态下的量子效应，并给出了电路中电荷和电流的量子涨落[1].然而，之后的近20年时间里，人们对于介观电路量子理论的研究几乎无多少进展.从20世纪90年代开始，一批物理学工作者围绕RLC及其耦合电路做了大量研究工作，在介观电路的量化方法、电路的量子力学效应等多方面取得了有意义的研究成果[2-5]，在国内外掀起了研究介观电路量子理论的热潮.

二极管是电路中的基本器件，含二极管的电路是典型的非线性电路，在实际的介观系统中经常出现.本文利用微扰理论来求解含二极管介观电容电感耦合电路系统的能级和波函数，进而讨论了系统的量子效应.研究含二极管的非线性电路的量子化，对介观电路量子理论的建立和应用有重要意义.

1 含二极管介观电路实例

含二极管介观电容电感耦合电路是从实际介观系统中抽取出的模型[6-7]，如图1 所示.

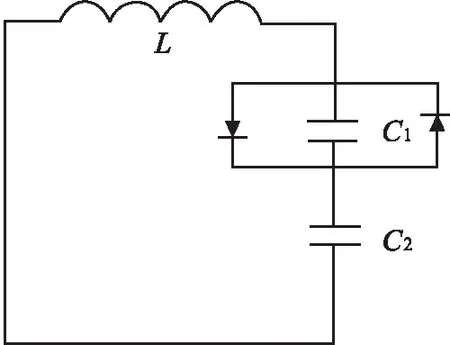
图1 含二极管的非线性介观电路Fig.1 Diodes included nonlinear mesoscopic inductive-capacitance circuit

运用基尔霍夫定律，可以得到电路中电荷满足的方程

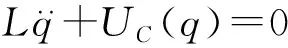
(1)

其中q代表2电容电荷总量，UC是2电容的电压降之和，UC的取值将随着q的变化而变化.当q值较小，二极管两端电压小于其导通电压时，此电路中的Ce等效为2个电容串联

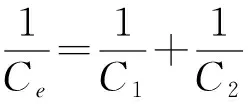
(2)

当电容两端电荷q增加到临界值qb及以上时，使二极管导通，C1被短接，这时电路中的等效电容为C2，其函数关系表达式如下：

(3)

将以上分段函数拟合成连续函数，可近似为

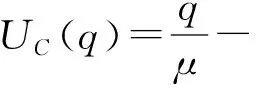
(4)

其中μ和ν为拟合系数[7].

由此可得此介观电路的拉氏量

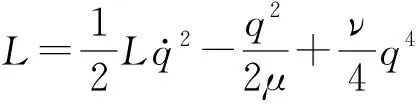
(5)

图1所示的电路，实际上是2个LC谐振电路的衔接，为了与简谐振子的哈密顿量对比，作如下系数变换：

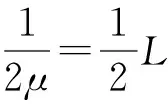
(6)

则体系的哈密顿量可以写为

.

(7)

理论上，已知了体系的哈密顿，可以通过求解薛定谔方程的方法对介观电路进行量子化求解.但是，由于势能项中含有电荷的四次方项，使得微分方程不能严格解析求解.文献[7]和[8]分别利用二次量子化方法和路径积分的方法研究了该系统，由于计算的复杂，也只得到了体系的基态能量.事实上，根据实际电路中ν的取值，λ可以为小参量[6]，因此本文所讨论的含二极管介观电容电感耦合系统可以用微扰理论求解.

2 含二极管介观电容电感电路量子化求解

体系的哈密顿分为2部分之和

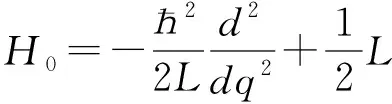
(8)

H0的表达式与线性谐振子的表达式完全相同，其本征方程为

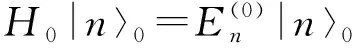
(9)

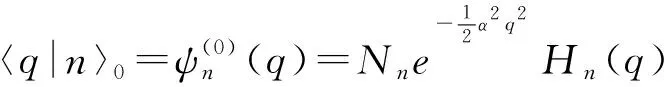
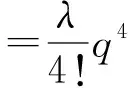
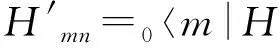
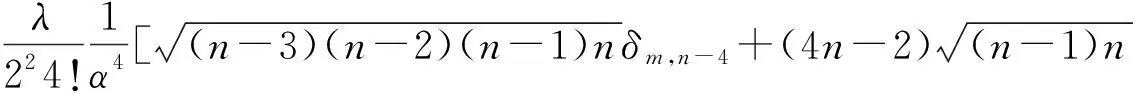
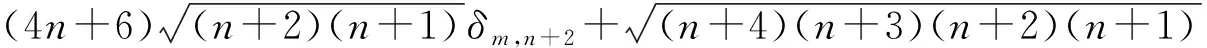
(10)

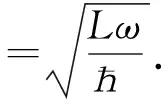
按照微扰理论，二级修正的能级和一级修正的波函数为

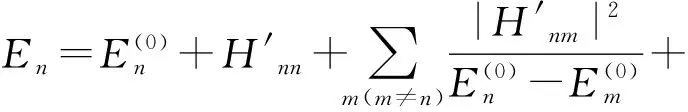
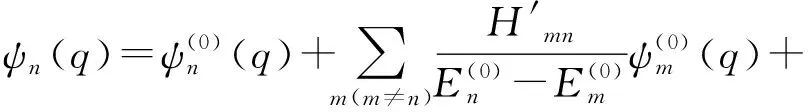
(11)

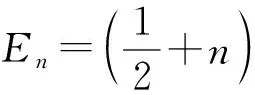
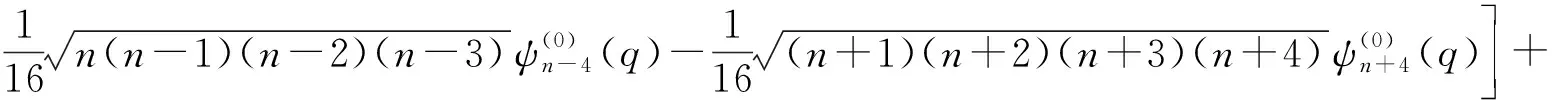
(12)

这就是含二极管介观电容电感电路二级修正的能级和一级修正的波函数.

上式中，令n=0，可以得到体系二级修正的基态能级和一级修正的基态波函数

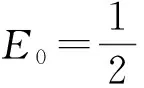
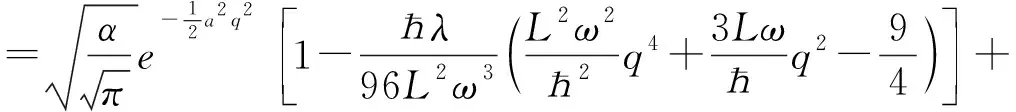
(13)

所得到的基态能级的表达式与文献[7]和[8]中的结果一致.

3 电荷的量子涨落

能级和波函数是描述量子体系重要的物理量，利用上面所得到的结果，可以进一步研究含二极管介观电容电感电路的量子力学效应.下面用前面的结果来计算体系电荷的量子涨落.

在体系的第n个本征态中，电荷和电荷的平方的平均值为

〈n|q|n〉=0；

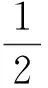
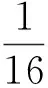
(14)

从计算结果发现：电荷的平均值不为零，可以计算出电荷的不确定性，根据不确定性原理，就可以得到电流的不确定性大小，电流的不确定性称为量子涨落，它对应电路中的量子噪声，量子噪声的大小由参量L，μ和ν共同决定.

4 结论

利用微扰法，对含二极管介观电容电感耦合电路进行了量子化求解，得到了体系二级修正的能级和一级修正的波函数.利用得到的波函数，计算了体系中电荷的量子涨落.与相关的研究工作相比较，本文的计算方法简单，而得到了一个比较精确的解，可以用来研究含二极管介观电容电感电路的其他量子力学效应，同时也是介观电路量子理论应用的推广.

参 考 文 献:

[1] LOUISELL W H. Quantum Statistical Properties of Radiation[M]. New York: John Wiley,1973:271-275．

[2] LI Youquan, CHEN Bin. Quantum theory for mesoscopic electric circuits[J]. Phys Rev,1996, B(53):4027-4032.

[3] JI Yinghua, LUO haimei, WU Yunyi. Behaviors of mesoscopic LC circuit in the external magnetic field[J]. Phys Lett , 2003, A(318):141-145.

[4] FAN Hongyi, LIANG Xianting. Quantum fluctuation in thermal vacuum state for mesoscopic LC electric circuit[J]. Chin Phys Lett，2000, 17(3):174-176.

[5] WANG Jisuo, SUN Changyong. Quantum effects of mesoscopic RLC circuit in squeezed vacuum state[J].Int J Theor Phys,1998,37:1213-1216.

[6] FLERACHERS E L M, JANSSEN H J, BEERDEN L. Piecewise linear anharmonic LRC circuit for demonstratingsoftandhardspring nonlinear resonant behavior[J]. Am J Phys , 1985, 53(6):574-577.

[7] ZHANG S, UM C I, YEON K H．Zero-point energy in a mesoscopic nonlinear inductance-capacitance circuit[J]. Chin Phys Lett，2002, 19(7):985-987．

[8] 侯伯元，云国宏，杨战营.路径积分与量子物理导引[M].北京：科学出版社，2008:61-69.