油田开发数据预测新方法

陈现军 刘 洪 王硕亮 赵朝文 周 璟

(1.西南石油大学石油工程学院， 成都 610500； 2.中法渤海地质服务有限公司， 天津 300452；3.重庆科技学院科研处， 重庆 401331； 4.中国地质大学， 北京 100083； 5.中国石油西南油气田分公司， 重庆 400021)

油田产量变化受地质因素、流体性质、开采方式、井网形式、增产措施和管理水平等诸多因素控制，既有确定性又有随机性。目前，油田产量预测方法有经验统计法和数值模拟法。实践证明，这2种方法对油田开发过程中的时变性和各种随机干扰因素具有较大的不适应性[1]。因此，本文探索一种将油田产量的历史数据看成是时间序列，并利用时间序列分析法对油田产量进行建模及预测的方法，实践证明，该方法能够获得较高的预测精度。

目前利用时间序列方法预测油田开发数据的研究较少，普遍采用的方法是利用单一变量时间序列构造预测模型。油田实际生产过程中，压力与产量有着密切的关系，仅利用单一变量时间序列模型，无法反映压力与产量之间的关系。

本文首次将多变量时间序列与支持向量机方法相结合，充分挖掘油田产量和压力之间的关系，构建了一种新型的油田开发数据预测模型。

1 模型建立与参数求解

1.1 多变量时间序列的相空间重构

对于一个复杂系统，由于实测时序是一维的，不能完整地反映系统随时间的演化过程和系统内在的本质特征。为了能够从时序中得到系统的几何结构，Packand等人采用时间延滞技术，把一维时间序列嵌入m维空间中：

X(t)=(x(t),x(t+τ),x(t+2τ),…,x(t+(m-1)τ))T

(1)

式中：X(t) —t时刻系统的状态；m— 嵌入空间中点集的维数。

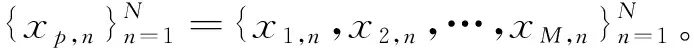
Vn=(x1,n,x1,n-τ1,…，x1,n-(m1-1)τ1;x2,n,x2,n-τ2,…,x2,n-(m21-1)τ2,…,xM,n,xM,n-τM,…,x1,M-(mM-1)τM)T

(2)

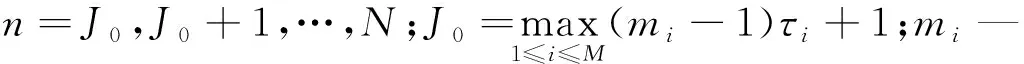
根据Takens定理，当系统嵌入维数m或mi足够大(m=m1+m2+…+mM>2D，D为吸引子维数)时，则存在确定性映射F：Rm→Rm使：V(n+1)=F(Vn)或者得到某一函数满足:Xi,n+1=fi(Vn),(i=1,2,3,…,M)。此时，状态空间Vn→Vn+1的演化反映了原未知系统的演化，这意味着原系统吸引的几何特征等价于重构的m维状态空间中吸引的几何特征。因此，原系统中任何微分或拓扑不变量可以在重构的状态空间中计算。

本文构建的m维空间包括地层压力、月产油量和月产水量，这3个指标是油田开发的基本指标，可以全面反映油田开发系统的实际状况。且3个指标间既相互关联又相互影响，本文采用多变量时间序列的预测方法，较单变量时间序列预测结果更为合理准确。

1.2 参数求取

1.2.1 延迟时间的求取

已知时间序列

X={xi|i=1,2，…,N}

将{xi}归一化，即

(3)

计算概率P(xi):

(4)

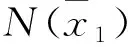
经过延迟后形成序列Y={yj|j=1,2,…,N-τ}={xj+τ|j=1,2,…,N-τ}

利用式(4)计算联合概率P(xi,yi)：

(5)

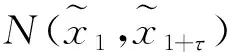
对于不同的延迟参数τ，计算互信息I(τ):

(τ) =H(X)+H(Y)-H(X,Y)

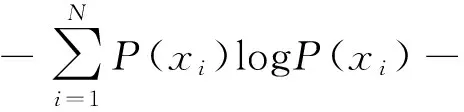
绘制τ-|(τ)曲线，将曲线第一次降到极小值时，对应的延迟时间τmin即为最佳延迟时间。

1.2.2 嵌入维数的选取

研究者提出了一种利用伪近邻法确定最佳嵌入维数的方法。假设已有时间序列X={xi|i=1,2,…,N}，则在d维相空间中重构的时间延迟向量为{yi(d)}：

yi(d)=(xi,xi+τ,…,xi+(d-1)r)

i=1,2,…,N-(d-1)

式中：d— 嵌入维数；τ— 延迟时间；yi(d) —d维嵌入空间中的第i个重构向量。

定义：

(6)

i=1,2,…,N-dτ

式中：yi(d+1) —d+1维嵌入空间中的第i个重构向量，即：

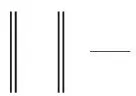
设a(i,d)的均值为

(7)

为了考察a(i,d)从d维重构相空间到d+1维重构相空间的变化情况，定义如下变量:

(8)

分析表明，如果时间序列产生于某个吸引子，则当嵌入维数d大于某值do时，E1(d)将停止变化，则可将do+1作为最佳嵌入维数。

1.3 基于支持向量机回归的时间序列预测模型

为了更有效的进行预测模型建模，首先对原始数据进行预处理，去除一些明显异常的点，然后对时间序列进行相空间重构，将一维的时间序列转化为矩阵形式，获得数据间的关联关系，以挖掘到尽可能多的信息量。给定恰当的嵌入维数m后，经过变换，得到用于支持向量机预测的学习样本：

(9)

确定了支持向量机预测器的拓扑结构，利用支持向量机对学习样本进行训练，回归函数为：

(10)

式中：t=m+1,…,ntr。

则预测模型为：

(11)

得到预测模型为：

(12)

2 实际应用

选取渤海油田某生产时间较长的生产井的月产油量、含水率、井底流压等数据，检验本文提出方法的准确性。选取原始数据的前90%的数据点作为学习样本，后10%的数据点作为检测样本。

(1)数据的预处理

在将实际数据输入时间序列模型之前，必须对其进行预处理，数据的预处理主要针对两种情况，一是异常数据点；二是关井情况。

对于异常数据点，需要手动将其删除，然后根据前后数据，对异常数据点对应的时间进行线性插值；对于关井情况，首先将关井的时间段内的数据删除，然后依据前后时间点的数据进行线性插值。

经过这样处理后的原始数据更加光滑，同时排除了人为因素的干扰，使预测模型得到更好的拟合精度与预测精度。

(2)相空间重构

选取月产油量、含水率、地层压力3个变量作为多变量时间序列预测的因变量。根据文中所述的参数选取方法，计算所得的延迟时间为3，嵌入维数为3。并进行三维变量的相空间重构。

(3)预测结果

分别用单变量时间序列法和多变量时间序列法对这口井的月产油量、含水率和地层压力进行了预测，预测结果分别如图1 — 图3所示。

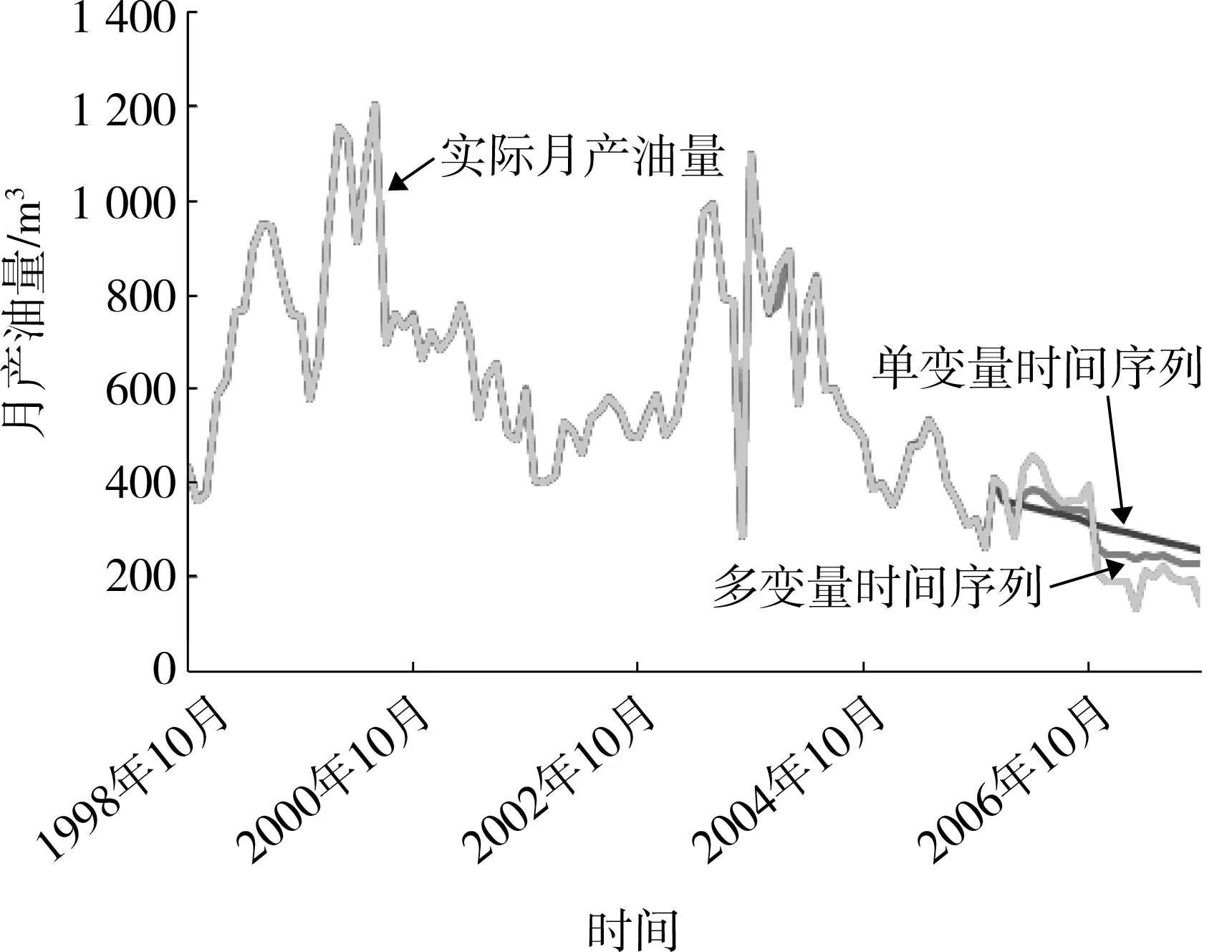
图1 月产油量预测结果图

图2 含水率预测结果图

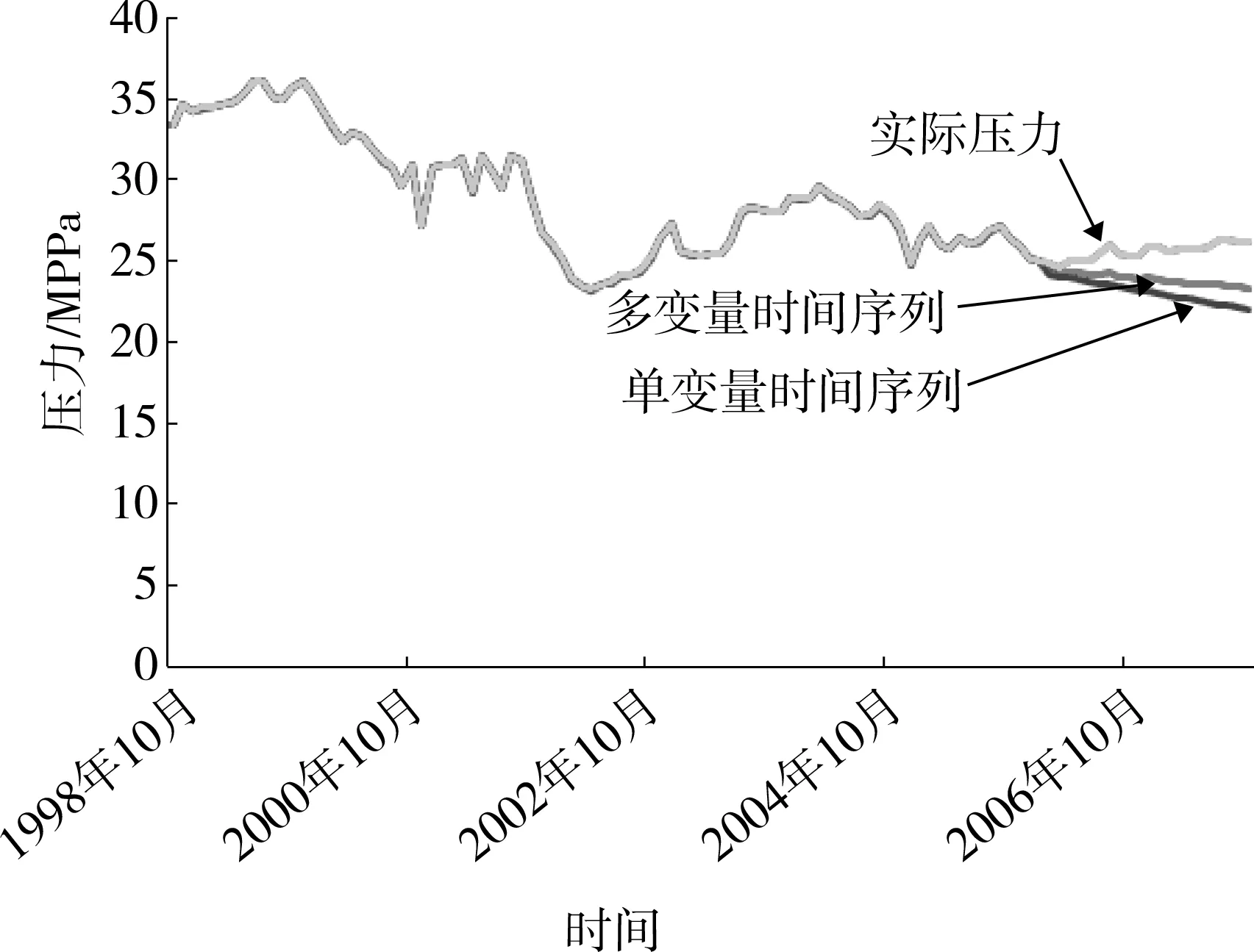
图3 地层压力预测结果图

多变量时间序列由于综合考虑了压力、产油量、产水量之间的相互关系，在长期变化趋势的预测方面要优于单变量时间序列预测方法。

统计预测5个时间步的预测结果，如表1所示。

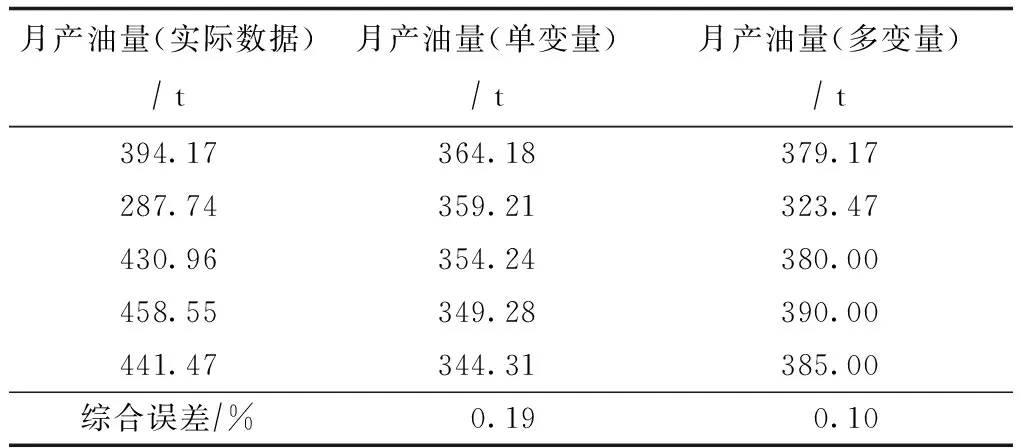
表1 月产油量预测结果统计表

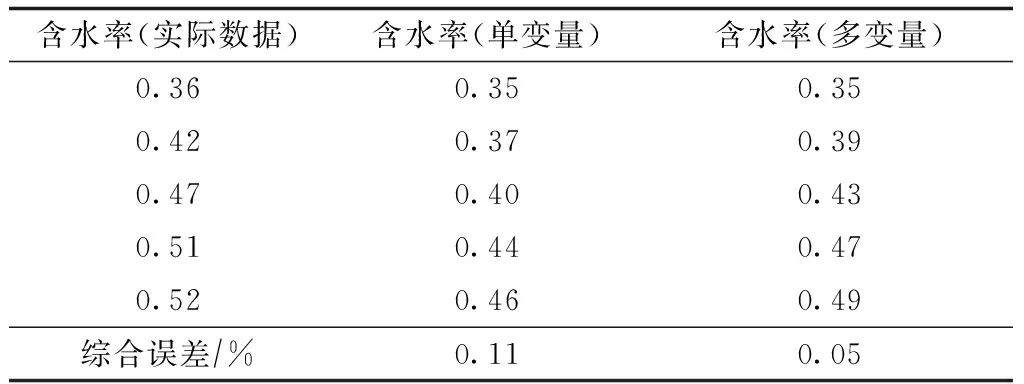
表2 含水率预测结果统计表

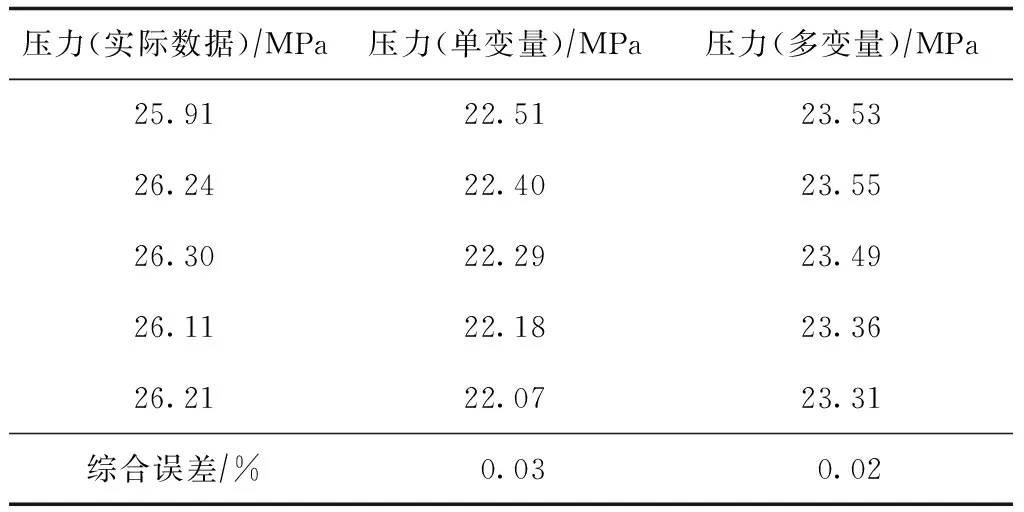
表3 压力预测结果统计表

从近5个时间点的预测结果看，用单变量时间序列方法和多变量时间序列方法对地层压力的预测准确性都较高，对月产油量的预测精度普遍偏低。总体来看，多变量时间序列预测结果好于单变量时间序列预测结果。

4 结 论

针对目前利用时间序列预测油田开发数据时存在的不足，提出利用多变量相空间重构技术预测油田开发数据的新方法。该方法克服了以往方法只单纯考虑单指标的变化规律，而未综合考虑系统内各指标相互影响的不足。经过实际计算验证，该方法无论从长期的变化趋势还是短期的精度预测，都优于单变量时间序列方法。

[1] 任宝生，赵明，刘志斌，等.油田开发动态指标的支持向量机预测[J].石油规划设计,2008,19(6):12-15.

[2] Michael Small.Applied Nonlinear Time Series Analysis:Applications in Physics, Physiology and Finance[J].World Scientific Series on Nonlinear Science Series A,2005,52:149-176.

[3] 钟仪华,杜志敏.特高含水油田开发规划动态预测方法研究[D].成都：西南石油大学,2008.

[4] 李小刚,杨兆中,伍晓妮,等.油井水力压裂后产量变化的混沌特征分析[J].断块油气田,2009(01):63-65.