高校消防安全评价及对策分析

李 律 康 钢 施金良

(重庆科技学院安全工程学院， 重庆 401331)

近年来，随着高校规模的扩大，后勤的社会化，校园安全出现了许多问题，其中消防安全问题就是一大顽疾，如2005年北京林业大学发生的火灾事故，2008年上海商学院发生的火灾事故等。这些事故都给个人及学校造成了极大的损失，留下了惨痛的教训。本文采用“二分变量—层次分析法”，对校园消防安全状况进行评价，提出解决对策。

1 “二分变量—层次分析法”简介

层次分析法(AHP)是应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法[1]。首先分析问题，再根据评估要实现的目标和达到的要求，将实际问题细化为若干个不同的指标，并对各指标按层次进行排列，形成递阶的多个层次分析的结构模型[2]。其次根据专家对指标之间的比较结果，运用层次单排序法得出各因素的权重值。通过层次总排序法得出指标层对中间层的权重，最后确定指标层相对于总目标的权重值。

二分变量法是评价两个特征变量相关程度的一种方法。对于某些离散型变量，如成功或失败，好或坏，生或死等，我们无法简单的进行定量评价，可以将它们转换为数值进行评价，如“成功为1，失败为0”，“男性为1，女性为0”。通过转换，从而进行数值相关性运算。

层次分析法能够评判某种因素相对总目标的重要程度，但无法评价当前某因素自身状况好坏。结合二分变量法，将调研数据量化，完成对当前各因素自身状况的评价，使评价结果更加清晰，更具有说服力。

2 “二分变量—层次分析法”应用于安全评价步骤

2.1 建立层次结构模型

将决策的目标、考虑的因素和决策对象按它们之间的相互关系分为目标层、中间层和指标层，绘出层次结构图。

2.2 构造判断矩阵

通过对同一层次的因素进行两两比较，按表1对各因素进行赋值，构成判断矩阵。

表1 判断矩阵标度赋值表

2.3 层次单排序及一致性检验

求出判断矩阵的最大特征根λmax以及对应的特征向量，经归一化后记为W。W的元素即为同一层次因素对于上一层次某因素的相对重要性权重，这一过程称为层次单排序。进行一致性检验：CI=(λmax-n)(n-1)，查表确定相应的平均随机一致性指标RI，计算一致性比率：CR=CIRI。当CR<0.1时，认为判断矩阵的一致性是可以接受的；当CR>0.1时,认为判断矩阵不符合一致性要求，需要对该判断矩阵进行重新修正。

2.4 层次总排序及其一致性检验

计算某一层次因素对于目标层相对重要性的权值：

Wi=Pij×qi

(1)

式中：Wi— 指标层各因素对总目标的权重；Pij— 指标层各因素对中间层的权重；qi— 中间层各因素对总目标的权重。

随后进行层次总排序的一致性检验：

(2)

判断方法同2.3。

2.5 调研数据的分析

运用二分变量法将调研数据定量化，按“0”、“1”进行打分，求出平均值。

2.6 评价结果分析

将各个评价因素权重与分数相乘，然后求和，得出最后分数，与指标量化准则[3](表2)比较，得出校园消防安全水平：

(3)

式中：S— 高校消防安全总得分；Wi— 指标层各因素对总目标的权重；fi— 指标层各因素得分情况。

表2 指标量化准则

3 应用实例

3.1 划分高校消防安全评价因素

在对全校学生进行调研以及对高校消防安全特点研究的基础上，按照火灾的影响因素将消防安全划分为人的不安全行为、物的不安全状态和安全管理3个方面，高校消防安全评价指标体系见图1。

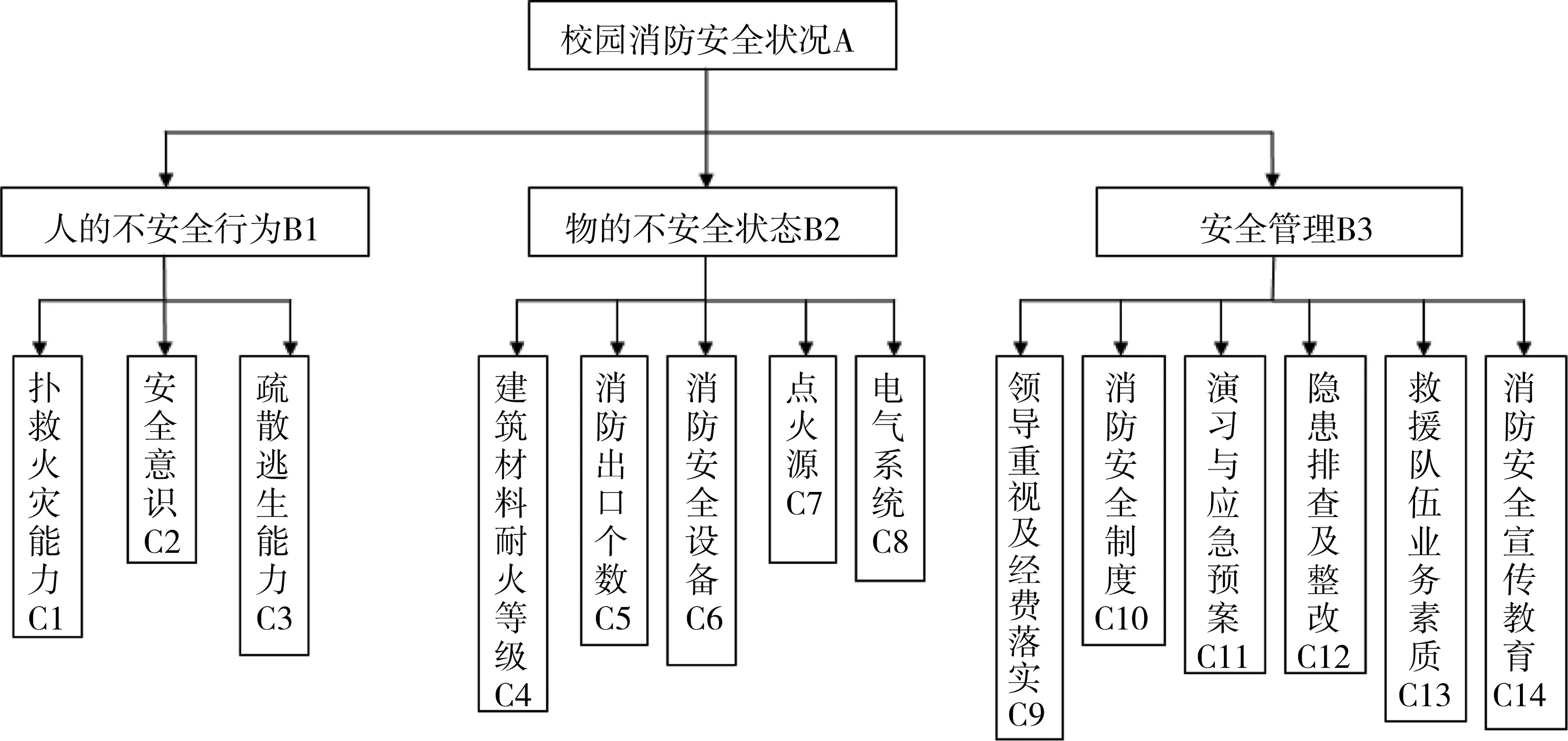
图1 高校消防安全评价指标体系

3.2 构造判断矩阵

组织专家分别对人的不安全行为(B1)，物的不安全状态(B2)和安全管理(B3)进行两两比较打分，得出判断矩阵：

特征向量W=(0.614 4, 0.268 4, 0.117 2)Tλmax=3.073 5,CI=0.036 75。查得RI= 0.58，则随机一致性比率CR=CIRI=0.063 4<0.1，通过一致性检验。

3.3 中间层对指标层建立判断矩阵

(1)人的不安全行为(B1)对应的3级指标判断矩阵为：

特征向量W=(0.163 4, 0.539 6, 0.296 9)Tλmax=3.009 2,CI=0.004 6。查得RI= 0.58，则随机一致性比率CR=CIRI=0.007 9<0.1，通过一致性检验。

(2)物的不安全状态(B2)对应的3级指标判断矩阵：

特征向量W=(0.049 7, 0.381 6, 0.259 2，0.122 3， 0.187 1)Tλmax=5.082 9,CI=0.020 7。查得RI=1.12， 则随机一致性比率CR=CIRI=0.018 5<0.1，通过一致性检验。

(3)安全管理(B3)对应的3级指标判断矩阵：

特征向量W=(0.345 0, 0.157 4, 0.064 1，0.256 8，0.091 6,0.085 1)Tλmax=6.323 4,CI=0.064 68。查得RI=1.24,则随机一致性比率CR=CIRI=0.052 2<0.1，通过一致性检验。

3.4 指标层对目标层的权重以及调研数据分析结果

以重庆科技学院在校大学生为调查对象，从13个学院一二年级学生中随机抽取了416人，以集中答题方式发放问卷试题共计416份，最终回收、筛选、录入有效问卷365份。问卷回收率为87.74%。通过分析试卷的各个统计量，找出与本文分析对象相对应的指标，按照二分变量法求出对应分数(表3)。同时，运用式(1)计算指标层对目标层的权重。CI=0.016，RI=0.802，CR=CIRI=0.02<0.1，通过一致性检验。

3.5 评价结果

用式(3)计算出人的不安全行为得分为70.88，评价结果为较好；物的不安全状态得分为73.61，评价结果为较好；安全管理得分为66.45，评价结果为一般；高校消防安全总得分为69.50，得出重庆科技学院消防安全状况为一般。说明我校消防安全总体状况还存在不少问题，还有许多地方有待加强安全防范。

4 对策分析

4.1 加强宣传教育，减少人的不安全行为

通过层次分析法可知，人的不安全行为占高校消防安全的权重最大，为61.44%。所以，减少人的不安全行为，能够大幅提升高校消防安全水平。首先，学校应将消防安全教育课纳入教学任务中，不定期开设消防安全知识课和培训课，使学生熟悉和掌握消防安全常识[4]。组织新生参加消防逃生演练，进行网上安全教育考试，达标者方能完成注册。其次，通过微博、微信、QQ等学生经常参与的网络新媒体渠道，以反面教材为例，增强消防安全防范意识，杜绝侥幸心理。最后，进一步发挥消防安全协会、消防安全志愿者的作用，组织开展消防知识竞赛等活动，促进学生消防安全意识、灭火能力及逃生技能的提高。

4.2 加大排查力度，将物的不安全状态降到最低

通过层次分析法可知，物的不安全状态在校园消防安全的权重中占26.84%。并且，物的不安全状态得分为73.61，仍有较大提升空间。首先，通过聘请专业安全评价公司定期对校园安全隐患进行排查，提出相应的改进措施；制定消防安全排查表，进行日常巡查工作。其次，以学校保卫处为主，联合学工部、总务处、后勤公司等相关部门以及学生群体组织，加大对学生寝室的巡查力度，及时治理私搭乱接现象，收缴电饭锅、烤火炉等大功率电器，告知人走电断，防止短路自燃现象，从源头上杜绝各种不安全隐患。最后，对于发现的各种隐患，要及时跟进，督促各个部门进行整改。制定相应的消防安全整改制度，对于未及时完成整改的，按规定给予相应处罚。

4.3 增强认识，加强安全管理

安全管理得分为66.45，评价结果为一般。特别是消防安全制度上，为较差，需要引起重视。首先，成立消防安全领导管理小组，由校领导作为第一责任人，做好党政各部门与保卫部门的协调工作以及经费预算落实工作。其次，建立健全消防安全制度，使消防安全工作有理可依、有章可循。层层签订消防安全责任状，明确目标任务，层层落实责任[5]。最后，加强对保卫队伍的管理与培训：一是培训队伍的业务能力，消防管理人员应熟练掌握消防法律、法规和建筑、电气防火的消防知识技能[6]；二是加大对安全保卫队伍“以人为本”意识的灌输，将管理为主转变为服务为主；三是加大奖惩力度，充分发挥经济杠杆作用，激发保卫人员工作积极性。

5 结 论

(1)运用“二分变量—层次分析法”将评价目标划分为14个指标层因素，将调研数据量化后，得出人的不安全行为对高校消防安全影响最大，重庆科技学院消防安全状况为一般。

(2)“二分变量—层次分析法”评价高校消防安全状况，既能评价各因素相对于总目标的重要程度，又能分析当前此种因素的优良状况，能够直接、准确、科学、可靠的分析高校消防安全状况。

[1] 费广成.基于层次分析法的城市火灾风险评价体系[J].常熟理工学院学报：自然科学版， 2013,27(2):52-56.

[2] 韩俊.基于层次分析法的政府门户网站评价模型研究：以浙江省11个地级市政府门户网站为例[J].图书馆学研究,2007(12):87-93.

[3] 张村峰，卞奇侃，蒋军成.基于“事故树 — 层次分析法”的高校学生宿舍火灾风险分析[J]. 中国安全生产科学技术，2011,7(10):100-105.

[4] 史楠.浅谈学校校舍消防安全工作的现状及对策[J].科技致富向导，2011(11)：52-55.

[5] 沈建军.浅析大学校园消防安全现状及对策[J].职业技术,2007(6):126.

[6] 张啸.浅析高校消防安全现状及对策[J].新西部，2008(2):26-27.