应用毛管压力资料确定相渗曲线参数的新方法

杨 洋 唐 玲

(1.西南石油大学石油工程学院， 成都 610500； 2.新疆独山子天利实业总公司树脂项目部， 新疆 克拉玛依 833600)

相对渗透率曲线是研究多相渗流的基础，它在油田开发计算，动态分析，确定储层中油、气、水的饱和度分布及与水驱油有关的各类计算中都是必不可少的资料。毛管压力和相对渗透率作为岩石的基本属性，都是(非)湿相饱和度的函数，它们之间存在一定的关系，在一定条件下可以相互转化。应用毛管压力资料计算相渗曲线的方法有：

Corey模型[1]：

krw=(S′)4

(1)

krnw=(1-S′)2[1-(S′)2]

(2)

其中：

(3)

式中：krw— 湿相相对渗透率；krnw— 非湿相相对渗透率；S′ — 有效湿相饱和度；Sr— 最小湿相饱和度，即毛管压力为无限大时的剩余湿相饱和度；Sw— 湿相饱和度。

由于Corey模型涉及到常数，对于不同孔隙分布的岩石，其计算结果仍一致，这与实际相差甚远。Brooks和Corey[2]对Corey模型进行改进，引入了岩石孔隙大小分布指数λ：

(4)

(5)

式中：λ— 孔隙大小分布指数。

当λ取2时，Brooks-Corey模型就变成Corey模型，说明Corey模型是一特例。李克文和Horne在测试毛管压力以及应用毛管压力资料计算相渗曲线方面做了大量研究,且提出了Li-Horne模型[3]：

(6)

(7)

Burdine模型[4]是在Purcell模型(Purcell模型是根据简单的毛管束模型推导出来的，与实际岩石的孔隙结构相差很大，故其精度很低)基础上引入了迂曲度的概念提出来的，提高了计算精度:

(8)

其中：

(9)

式中：λrw— 湿相弯曲度比值；Smin— 最小湿相饱和度；τw(1.0),τw(Sw) — 分别为湿相饱和度为100%和Sw时的弯曲度。

(10)

其中：

(11)

式中：λrnw— 非湿相弯曲度比值；Snw— 非湿相平衡饱和度。

前3种模型涉及到参数λ的确定，Standing指出孔隙大小分布指数λ与岩石孔隙尺寸分布范围和分布频率等有关。很多学者展开了λ与岩石孔隙尺寸分布范围、频率关系的研究[5-7]，但其研究只停留于定性关系上，并未给出它们之间的定量关系；而关于λ的应用[8]，文中也都是凭经验直接给出，存在着很大的误差。本次研究以压汞实验为基础，通过毛管压力定量数学模型(模型表达式中含λ)拟合实验实测点来确定λ值。由式(8)、(10)可以看出Burdine模型公式表达式较为复杂，涉及到迂曲度。为了简化计算，可以结合其分形几何表达式，只涉及到分形维数D，而D可以通过毛管压力的分形公式求出。

1 λ值的确定

研究选用压汞法测取的毛管压力曲线如图1所示。

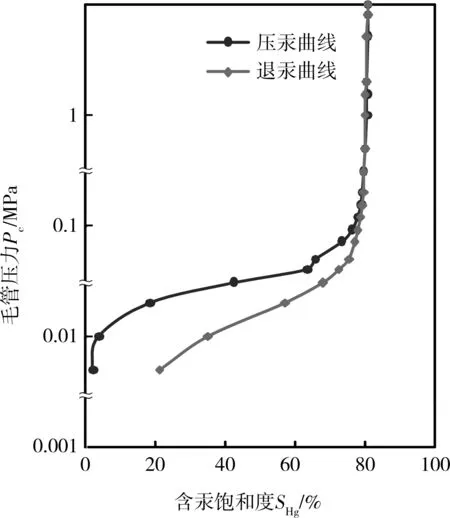
图1 毛管压力曲线

选用的毛管压力定量数学模型为Gerhard-Kueper模型[10]，因为该模型比较成熟，是Brooks-Corey毛管压力定量数学模型的延伸，其第一次驱替曲线仍采用Brooks-Corey模型表达式，定义如下：

Pc=PD(S′)-1/λd

(12)

式中：PD— 第一次驱替曲线延伸到湿相饱和度Sw=1.0时的毛管压力；S′ — 有效湿相饱和度；λd— 与驱替过程有关的孔隙大小分布指数。

吸入曲线定义为：

(13)

在参考了文献[11-12]后，由毛管压力曲线确定参数值图2结合本次实验实测曲线得出各参数值，见表1。

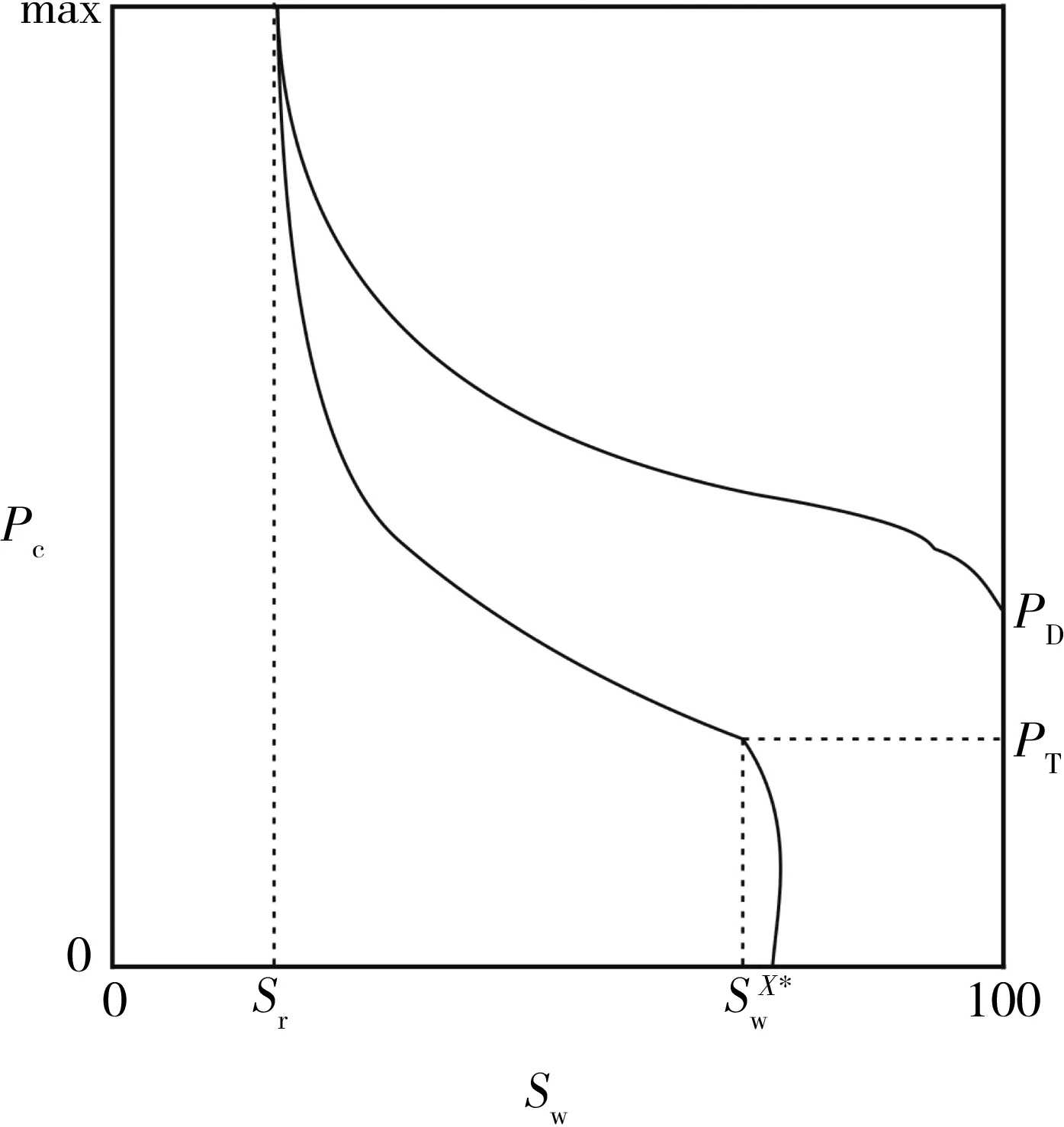
图2 毛管压力曲线确定参数值图

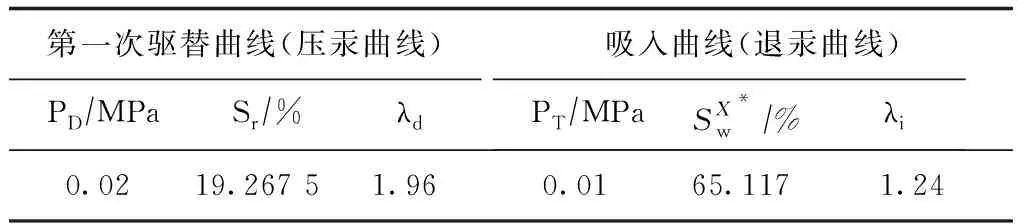
第一次驱替曲线(压汞曲线)PD∕MPaSr∕%λd吸入曲线(退汞曲线)PT∕MPaSX*w∕%λi0.0219.267 51.960.0165.1171.24

模型驱替曲线与压汞实测点的拟合情况见图3；模型吸入曲线与退汞实测点的拟合情况见图4。

图3、4的拟合效果较好，由此确定出孔隙大小分布指数λ的正确性，由于毛管压力的孔隙分布主要由第一次驱替判定，因此计算相渗公式中λ取值为第一次驱替曲线的分布指数λd。

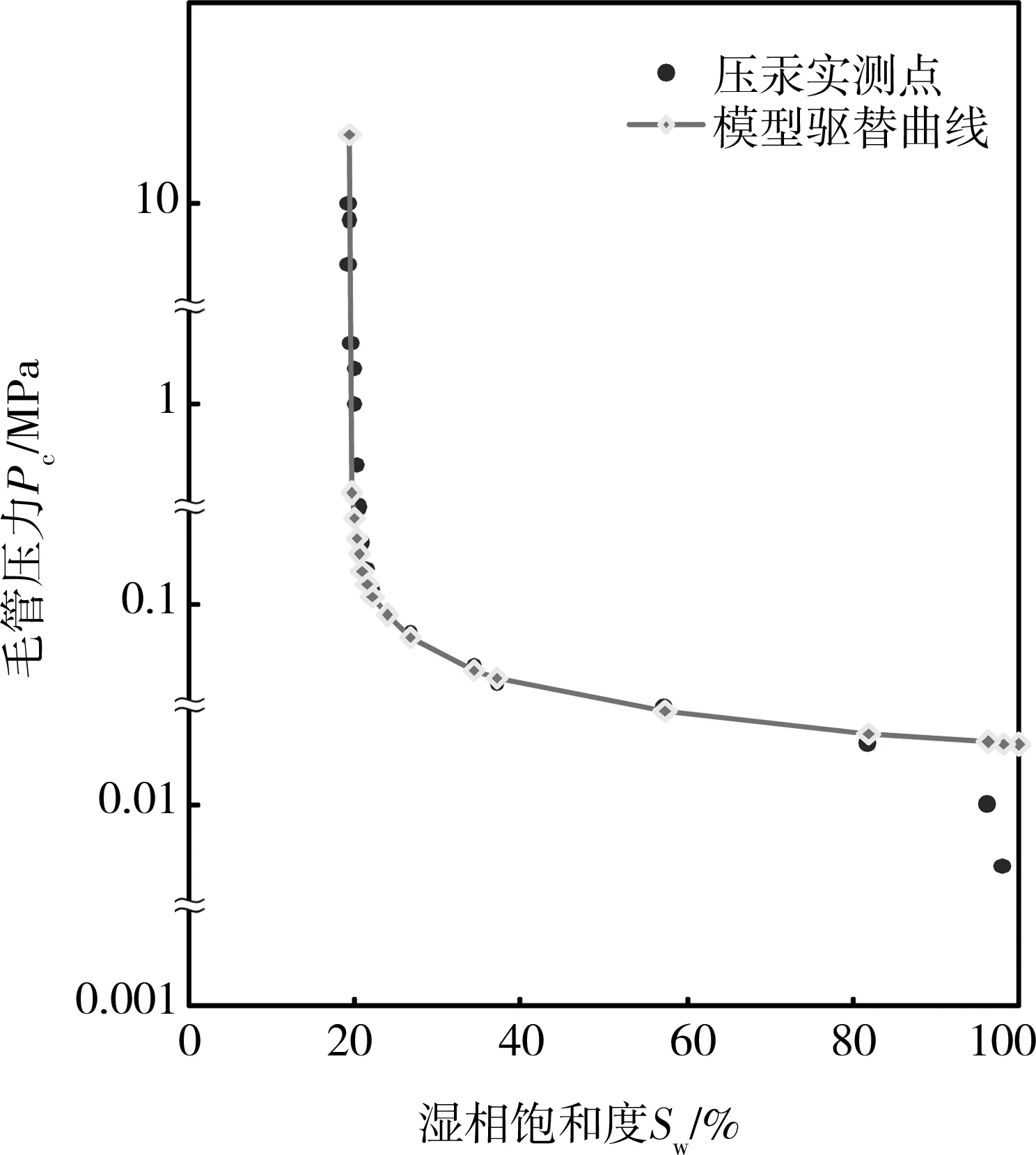
图3 驱替拟合图

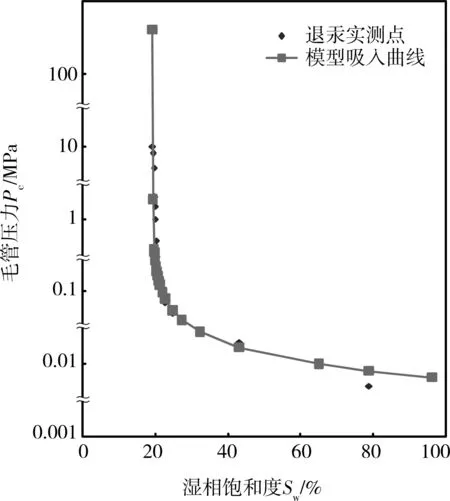
图4 吸入拟合图

2 分形维数D的确定

前人研究结果表明，可以用分形几何学来描述经典欧几里德难以描述的复杂不规则的岩石孔隙结构，储层岩石孔隙尺寸在0.2～50 μm范围具有很好的分形特征。1998年贺承祖[13]结合分形理论，推导出了毛管压力曲线和相渗的分形几何公式：

(14)

式中：Pmin— 储层中最大孔径rmax对应的毛管压力，即入口毛管压力；S— 湿相饱和度。

(15)

(16)

对式(16)两边取对数，得：

lgS=(3-D)lgPmin+(D-3)lgPc

(17)

根据压汞实验实测点(在退汞过程中，有一定量的汞滞留在岩石孔隙中，退汞不能正确反应岩石孔隙结构，因此此处拟合压汞实验主要实测点)，对lgS～lgPc双对数作图得到一条直线(见图5)，由直线斜率可求出分形维数D(D约为2.33)，代入式中即可求出相对渗透率。

3 计算实例

将前面确定的参数λd和分形维数D，结合实验测试数据，分别代入4个模型中，得到相渗曲线如图6所示。从图中可以看出，以分形维数D为桥梁结合分形几何式计算出的相渗曲线与前几种模型计算结果相差不大，而且算法更为简单；分形维数还可以用于评价岩石的非均质性。

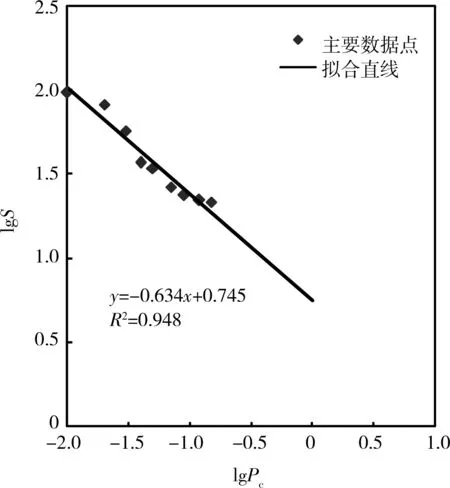
图5 lgS～lgPc双对数图

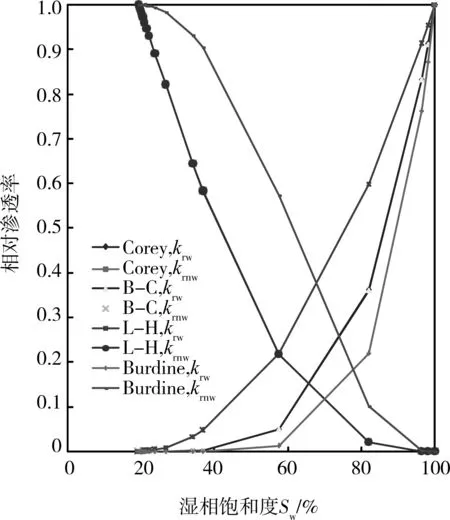
图6 相渗曲线

4 结 论

(1)提出了通过拟合实验数据确定孔隙分布指数λ值，比凭经验取值可靠，更有理论依据。

(2)提出计算相渗曲线更简单的方法，即通过拟合毛管压力资料求出分形维数D，进而计算出相对渗透率。

[1] Corey A T.The Interrelation Between Gas and Oil Relative Permeabilities[J].Prod.Mon.,1954,19(1):38-41.

[2] Brooks R H,Corey A T.Hydraulic Properties of Porous Media[J].Colorado State University Hydrology Papers,1964:72-80.

[3] Li K,Horne R N.Comparison of Methods to Calculate Relative Permeability from Capillary Pressure in Consolidated Water-wet Porous Media[J].Water Resources Research,2006,14(6):42-54.

[4] Burdine N T.Relative Permeability Calculations from Pore Size Distribution Data[J].Trans.AIME,1953,19(8):71-79.

[5] Mccuen R H,Rawls W J,Brakensiek D L.Statistical Analysis of the Brooks-Corey and the Green-Ampt Parameters Across Soil Textures[J].Water Resources Research,1981,17(4):1005-1013.

[6] Bloomfield J P,Gooddy D C,Bright MI,et al.Pore-throat Size Distributions in Permo-Triassic Sandstones from the United Kingdom and some Implications for Contaminant Hydrogeology[J].Hydrogeology Journal,2001, 9:219-230.

[7] Cary J W,Hayden C W.An Index for Soil Pore Size Distribution[J].Geoerma,1973,9(4):249-256.

[8] Mark L Porter,Dorthe Wildenschild,Gavin Grant,et al.Measurement and Prediction of the Relationship between Capillary Pressure,Saturation,and Interfacial Area in a NAPL-water-glass Bead System[J].Water Resources Research,2010,46:1-10.

[9] 何更生.油层物理[M].北京：石油工业出版社，1994:11．

[10] Gerhard J I,Kueper B H.Capillary Pressure Characteristics Necessary for Simulating DNAPL Infiltration,Redistribution,and Immobilization in Saturated Porous Media[J].Water Resources Research,2003,39(8):1-12.

[11] Muhammad Sahimi.Flow Phenomena in Rocks:from Continuum Models to Fractals,Percolation,Cellular Automata,and Simulated Annealing[J].Reviews of Modern Physics,1993,65(4):1393-1534.

[12] Assouline S.On the Relationships Between the Pore Size Distribution Index and Characteristics of the Soil Hydraulic Functions[J].Water Resources Research,2005,41:1-13.

[13] 贺承祖，华明琪.储层孔隙结构的分形几何描述[J].石油与天然气地质，1998,19(1)：15-23.