经济增长与环境污染的协整关系研究——基于2001—2010年江苏省各地区面板数据*

柳 阳,唐姜贤,靳旭东

(兰州商学院 统计学院,甘肃 兰州 730020)

许多学者利用各种数据来验证EKC(环境库兹涅茨曲线)的存在性,对EKC进行实证分析的数据主要有截面数据、时间序列数据和面板数据。由于单纯运用截面数据或时间序列数据去验证EKC假说都存在一些不足,因此更多的学者开始利用面板数据来检验EKC的存在性,但是由于使用的数据或模型不同,所得的结论也不尽相同。

由于经典回归模型假设所涉及的变量都是平稳的,当数据为单整的时间序列时,可能产生伪回归。由于面板数据相比单纯的截面数据或时间序列数据具有更大的自由度,且能够使EKC同时具有时序特征和截面特征,因此采用面板数据对EKC的长期关系进行验证,利用面板单位根和面板协整两种方法来检验江苏省经济增长与环境污染之间的长期EKC关系是否成立。并在此基础上对变量之间的关系进行估计,进而对江苏省环境污染与经济增长之间的变化关系进行分析。

一、面板单位根和协整检验的方法

(一) 面板数据的单位根检验

(1) 相同根情况下的单位根检验方法:LLC检验、Breitung检验；(2) 不同根情况下的单位根检验方法:IPS检验、Maddala和Wu检验。

(二) 面板数据的协整检验

Pedroni 协整检验利用下面方程的残差进行:

yit=αi+βixit+tδi+uit。(t=1,2,…,T;i=1,2,…,N)

Pedroni以回归残差构造了7个统计量:假设不同横截面具有相同的回归系数时,得到四个组内维度描述统计量,分别记为PanelADF、PanelPP、Panelrho、Panelv。假设不同的横截面具有不同的回归系数时,得到剩余三个组间维度描述统计量,分别记为GroupADF、Grouprho、GroupPP。这 7 个统计量的渐进分布都具有下面的形式:

二、数据来源和模型描述

本文采用的污染排放指标为二氧化硫排放量,使用人均GDP来衡量经济的增长,数据来源于2001—2010年各期《江苏省统计年鉴》。

采用三次多项式的简化模型来进行分析,其中仅包含了人均GDP作为变量,没有考虑贸易、技术进步、经济结构等对环境的影响,模型表达式为:

以上的每一个变量均为面板容量,其中i为地区指标(i=1,2,…T),t为时间指标(t=1,2,…,T),αi为特定的截面效应,uit为随机扰动项,lnEit表示第i个地区在第t年的二氧化硫排放量的对数,lngdpit表示第i个地区第t年的人均GDP对数的平方。

三、数据的检验结果及描述

(一) 面板数据的单位根检验

利用Eviews软件对数据进行分析,面板单位根结果如表1所示。表1显示，各种检验方法的检验结果并不完全统一。就lnEit来说,五种检验方法一致认为其并非平稳,而对于一阶差分lnEit,是平稳序列,因此认为lnEit是I(1)过程。对于lngdp、lngdp2和lngdp3而言,LLC检验、FisherADF检验、Breitung检验、IPS检验和FisherPP检验都认为其为非平稳序列,而对于其一阶差分五种方法都认为已经平稳,所以以上三个指标变量都为I(1)过程。

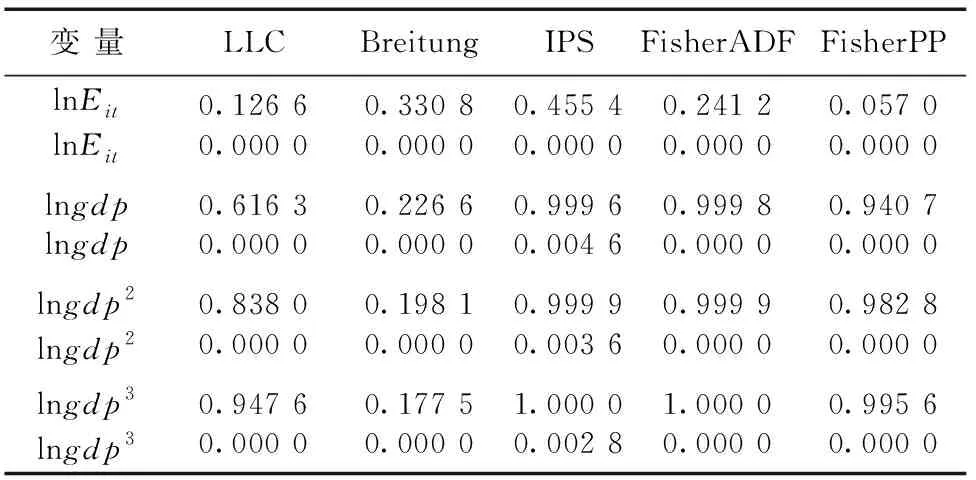
表1 面板数据单位根检验结果

注:检验形式设定为:含截距不含趋势项,显著性检验水平为5%。

(二) 面板数据的协整关系检验

根据单位根检验结果可知,解释变量lngdp、lngdp2和lngdp3都是一阶单整的,且lnEit也是一阶单整的,所以SO2排放量与人均GDP之间可能存在协整关系。为了进一步验证协整关系的成立,利用三种面板协整检验方法分别对其进行检验,结果见表2。

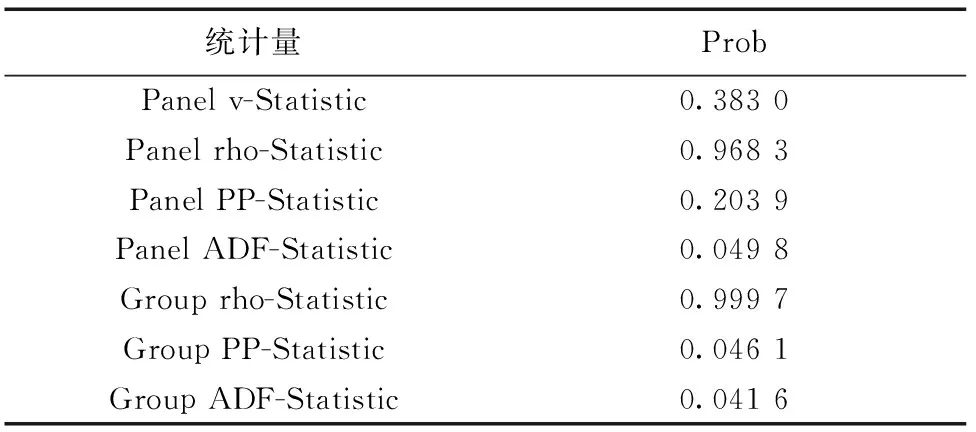
表2 面板数据的检验结果

注:以上显著性检验水平为5%。

由表2知,协整检验的 Panel 统计量中,Panel v-Statistic、Panel PP-Statistic 和 Panel rho-Statistic对应的P 值均大于 5%的置信水平,因而不拒绝其原假设,即认为变量之间不存在协整关系。Panel ADF-Statistic、Group PP-Statistic 和Group ADF-Statistic 的值均小于 5%,拒绝其原假设,认为变量之间存在协整关系。Pedroni检验结果不一致,但根据 Pedroni的结论,Panel ADF 和Group ADF的检验效果最好,Panel v和Group rho检验效果最差,其他处于中间。因此,人均GDP与二氧化硫排放长期均衡关系存在。

(三) 面板数据模型的选择与估计

由于人均GDP与二氧化硫排放的协整关系是成立的,故可对其长期关系进行建模分析,其静态面板数据模型的一般形式为:yit=αi+xitβi+uiti=1,2,…,N;t=1,2,…,T,其中xit为1×K向量,βi为K×1向量,K为解释变量的个数。但根据因变量Y的自变量的系数在所有横截面样本点和时间上是否都相同可以将静态面板数据分为混合模型、变截距模型和变系数模型等三种形式。如表3所示。

表3 静态面板数据模型的3种形式

建模前要检验所研究的问题适合于应用表3中的哪种模型形式。目前使用较为广泛的方法是协方差分析,具体过程是检验下面的两个假设:

正是从这个意义上说，作为食品行业的先锋代表，改革开放四十年的功勋人物、领军人物为推动行业品牌的树立、品牌化发展做出了突出贡献，而示范品牌企业则为行业可持续发展提供了标尺，起到引路灯、领航船的作用。

假设 1:在不同的横截面样本点上和时间上,截距不同而斜率都相同,即

H1:yit=αi+xitβ+uit。(i=1,2,…,N;t=1,2,…,T)

假设 2:在不同的横截面样本点和时间上,截距和斜率都相同,即

H2:yit=α+xitβ+uit。(i=1,2,…,N;t=1,2,…,T)

首先对假设2进行检验,如果不拒绝假设2,就无需检验假设1,选用表3中的模型III。如果上一步的检验拒绝了假设2,就应该进一步对假设1进行检验。如果假设1被再次拒绝,就应该采用表3中的模型I来设定研究问题的模型;若未被拒绝,则可用模型II。检验假设2和假设1的过程如下:

设S1、S2、S3分别为模型yit=αi+xitβi+uit,yit=αi+xitβ+uit以及yit=α+xitβ+uit的残差平方和。那么检验假设1的F统计量为:

检验假设2的F统计量为:

给定显著水平(常用的显著水平为 5%或 1%),查对应的F分布表,得到临界值,再跟上述计算得到的F统计量(F1和F2)进行比较,如果计算值小于临界值则接受原假设,否则就拒绝原假设,从而确定模型的形式。通过计算得到:S1=14.809 40,S2=26.595 26,S3=99.807 36。

从假设2,即截距以及斜率在不同的横截面样本点和时间上均相同,开始检验。

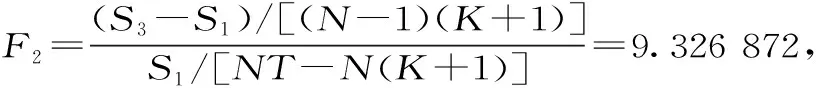
F2>F0.05(48,78)=1.531 305 113 6拒绝原假设2,即不能认为面板数据模型截距和斜率都相等。从而继续检验假设1。

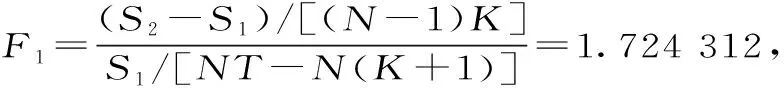
F1>F0.05(36,78)=1.568 149 385 25,拒绝原假设1,认为面板数据模型截距和斜率都不相等,即截距不相同,斜率在不同的横截面样本点上和时间上也不相同。于是最终的模型形式为固定变系数模型,不能假定系数β相同。

选择江苏省13个地市样本,通过 Eviews 运行数据最终得到的各地市的面板数据方程的系数如表 4。

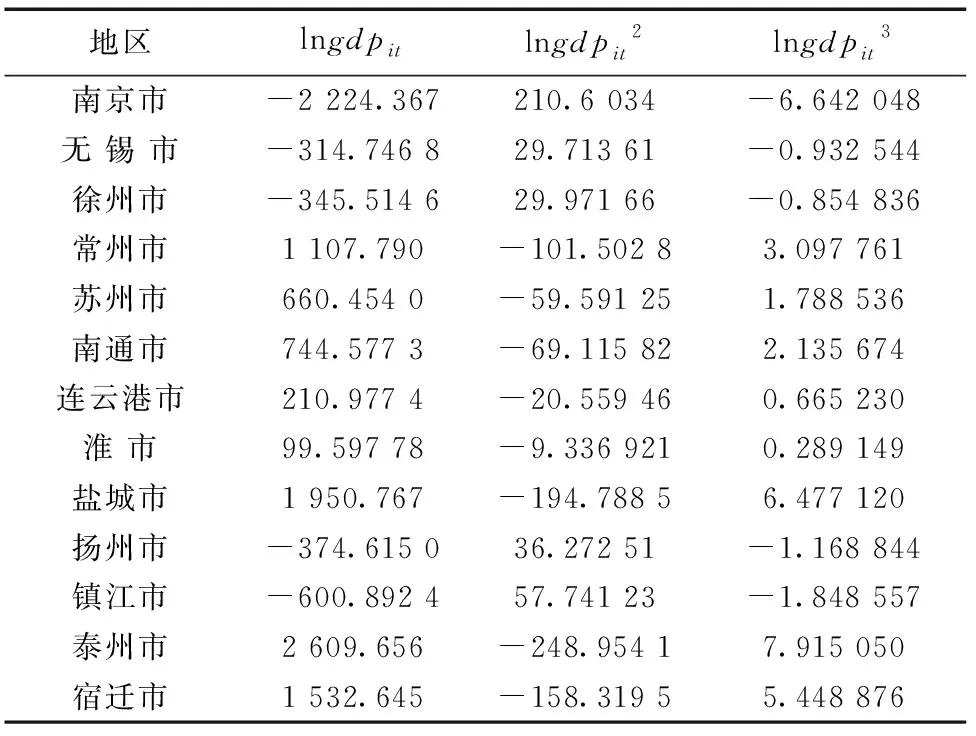
表4 变系数固定影响模型估计结果

江苏13个地市研究的样本是总体的所有个体,面板数据模型选用固定影响模型。根据表4,还可运用R软件对各地市人均GDP与二氧化硫排放的曲线关系进行模拟(略)。

四、结论

综上实证分析表明,江苏省各地市人均GDP与二氧化硫排放之间的关系都不满足EKC假设。因此用单一的环境EKC来解释江苏省环境污染与经济增长之间的关系是不太合理的,不能误认为改善环境质量的关键途径是加速经济增长。虽然南京市、无锡市、徐州市、扬州市、镇江市关于环境污染和人均GDP关系的估计给出了比较乐观的结论:经济增长能降低环境污染。但没有证据表明如果没有政策的推动和激励,这一过程能自动完成。如果要阻止环境进一步恶化,只能通过一定的政策和激励来减少各企业每单位产出的污染强度,或通过产业转移,从多污染产业向少污染产业转移。因此仅仅依靠EKC结论不能作为“先污染,后治理”的借口,为了改善环境质量应该制定相应的环境保护政策。

参考文献:

[1] 李国柱.经济增长与环境污染:基于面板数据单位根的研究[J].石家庄经济学院院报,2007(3):63-66.

[2] 郭军华,李帮义.中国经济增长与环境污染的协整关系研究——基于1991—2007年省级面板数据[J].数理统计与管理,2010(2):281-293.

[3] 董涛.基于面板数据的我国房地产业对宏观经济的影响研究[D].北京:清华大学,2011.

[4] 贺彩霞,冉盛茂.环境污染与经济增长:基于省际面板数据的区域差异研究[J].中国人口资源与环境,2009(2):56-62.