形象化教学方法在振动力学课程中的应用研究

毛灵涛，刘 庆，刘红彬

(中国矿业大学(北京) 力学与建筑工程学院，北京 100083)

形象化教学方法在振动力学课程中的应用研究

毛灵涛，刘 庆，刘红彬

(中国矿业大学(北京) 力学与建筑工程学院，北京 100083)

振动力学是一门具有很强工程背景的专业基础课程，以工程实例中抽象出来的模型作为研究对象，采用力学与数学方法进行分析。课本中大量理论公式推导与计算增加了学生学习与理解的难度。根据振动力学课程的特点和学生学习心理，笔者阐明了形象化教学的必要性，提出了形象化教学的4个原则，即熟悉性、层次性、能动性和适当性，同时给出了形象化教学的应用实例。

振动力学课程；形象化教学方法；MATLAB

振动力学是一门工程背景很强的技术基础课程，是国内外高等工科院校各主体学科必须开设的一门重要的专业技术基础课，也是各力学本科、研究生专业的主干课程[1]。学生在接触振动力学之前，已学习了高等数学、线性代数、理论力学、机械原理和材料力学等课程，为振动力学的学习奠定了知识基础，但振动力学课本中大量的理论公式推导与计算依然令学生在心理上产生一定的恐惧感。

振动力学研究的对象是从生活、工程实例中抽象与概化出来的各类模型，采用力学及数学的方法分析其振动响应。在振动力学的教学中，不但不能抽象灌输和机械重复地讲述理论与公式的推导，而且必须将理论化、模型化的东西形象化、工程化，以富有引导性、启发性的讲述将教学内容通俗化、形象化，促进学生对所学知识的深入理解与应用，在有限的课时教学中，最大限度地提高学生可接受的信息量及对工程实际问题的初步分析能力，进而取得更好的教学效果。形象化教学已在许多课程中应用[2-4]。本文主要探索形象化教学方法在振动力学教学中的应用。

一、振动力学课程形象化教学的必要性

振动力学课程特点是公式推导计算多、模型多及工程性强。虽然在振动力学中存在大量前期所学课程应用的内容，如单自由度的运动微分方程的求解，其实就是高数微分方程的求解，多自由度求解频率及振型的过程就是线性代数中求解特征值与特征向量的过程等，但是之前知识学习的不扎实，导致在学习振动力学时感到困难。此外，振动力学课程学习时有限，在中国矿业大学(北京)是48个学时，内容涉及单自由度、多自由度、连续体及近似计算，即要结合机械振动，又要结合结构振动、所以要想上好本课程，并保证较好的教学质量，就得认真分析学生听课的心理特点，研究适合本课程的教学方法。

学生听课的过程就是视知觉的感受过程和思维的加工过程，依据知觉心理学中对创造性思维的研究，人在视知觉过程中, 总会自然而然地有一种追求事物完整的结构整体性或守形性的特点[4]。振动力学课程采用的是多媒体教学方式，学生主要通过视觉来感知新知识，想要让学生建立感性认识与理性认识的快速统一，将形象化教学方法引入到教学过程中是非常必要的。采用传统教学与多媒体教学相结合，以形象化教学为形式，引导学生视知学的理性作用，即所谓的视觉思维功能，将形象化的元素与抽象理论知识相结合，培养学生理解能力及创新思维能力，探索反映振动力学课程特点的行之有效的教学之路。

二、振动力学课程形象化教学的原则

形象化教学也称立体化教学法，是在教学过程中应用比喻、对比等教学手法，辅以实物、模型、图片、声音和视频等直观教学手段来丰富学生的感性认识，启发和引导学生进行形象化思维和想象，促进学生思维上实现从具体到抽象，从感性到理性的飞跃[4]。但在振动力学课程形象化教学中，不能是简单的素材的罗列与演示，应结合直观教学手段，从教学方法、手段和语言等多方面进行研究与设计。振动力学课程形象化教学的原则应遵循以下几点：

1.熟悉性原则。尽量使用与学生认知结构具有相似性、相关性的形象化信息，将新的知识点与一些学生熟悉的事例或已学的知识点相结合，更深层次的去认识事物，分析现象，这样易引发兴趣。

2.层次性原则。根据不同情况，设计不同问题的形象情境，可有效激发学生的思维。

3.能动性原则。形象化教学最终目的是让学生掌握由抽象到形象的思维方法，能在老师诱导下，主动将知识点与自己所知的形象化情境相联系，体验到创新的成就感，利于知识点的掌握。

4.适当性原则。形象化实例不易过多，充分利用学生对形象化事例新奇的第一印象即首因效应，把一个形象化实例分析透彻，而更多的例子可以留给学生课后思考。

三、形象化教学的实例

(一)力学模型的形象化

力学问题的研究首先是对研究对象进行模型化。在教材中，多是以模型化后的问题进行分析。学生首先接触到是约束、杆件及载荷等构成的简化模型，而对于相对应的原型书中没有介绍，学生也只能是死记分析的方式。而在形象化教学中，就需要老师把这些抽象化，简化后的模型再逆向原型化。如简支梁振动的分析，可以让学生想象单杠的横梁，人下杠的瞬间，由于横梁具有了初始的位移，横梁将产生低频振动；又如对于弦的振动，当分析弦长对弦振动频率影响时，可以让学生想象在听吉他弹凑时，左手不同把位改变着弦长，产生不同的音色，而人拨弦，就是相当于外加的激励，使弦具有不同的初始位移，速度或是加速度，通过形象化的说明，使学生能够将所学知识点与生活中的具体事物联系起来，加深理解。

利用力学模型分析实际问题，即形象化了模型，又让学生学会如何去分析问题，达到学以至用的目的。如图1所示锻锤机振动模型分析[5]，锻锤由框架，落下的锤头，砧座和基础构成，如图1(a)所示。砧座通常放在一个弹性垫上，以减少传到基础和框架上的振动。作为初步分析，框架，砧座，弹性垫，基础和土壤可以简化为一个单自由度系统，如图1(b)。作为改进模型，框架，砧座和基础可以分开，从而简化为一个两自由度系统，如图1(c)。如果想对模型继续改进，可以考虑锤头偏心的影响，这时每个质量块除了在纸面内竖向运动，还有纸面内的转动。通过一个实例分析，能够将所学内容充分展开，形象的阐述了单自由度，两自由度模型的应用，引导学生继续深入分析，达到良好的教学效果。

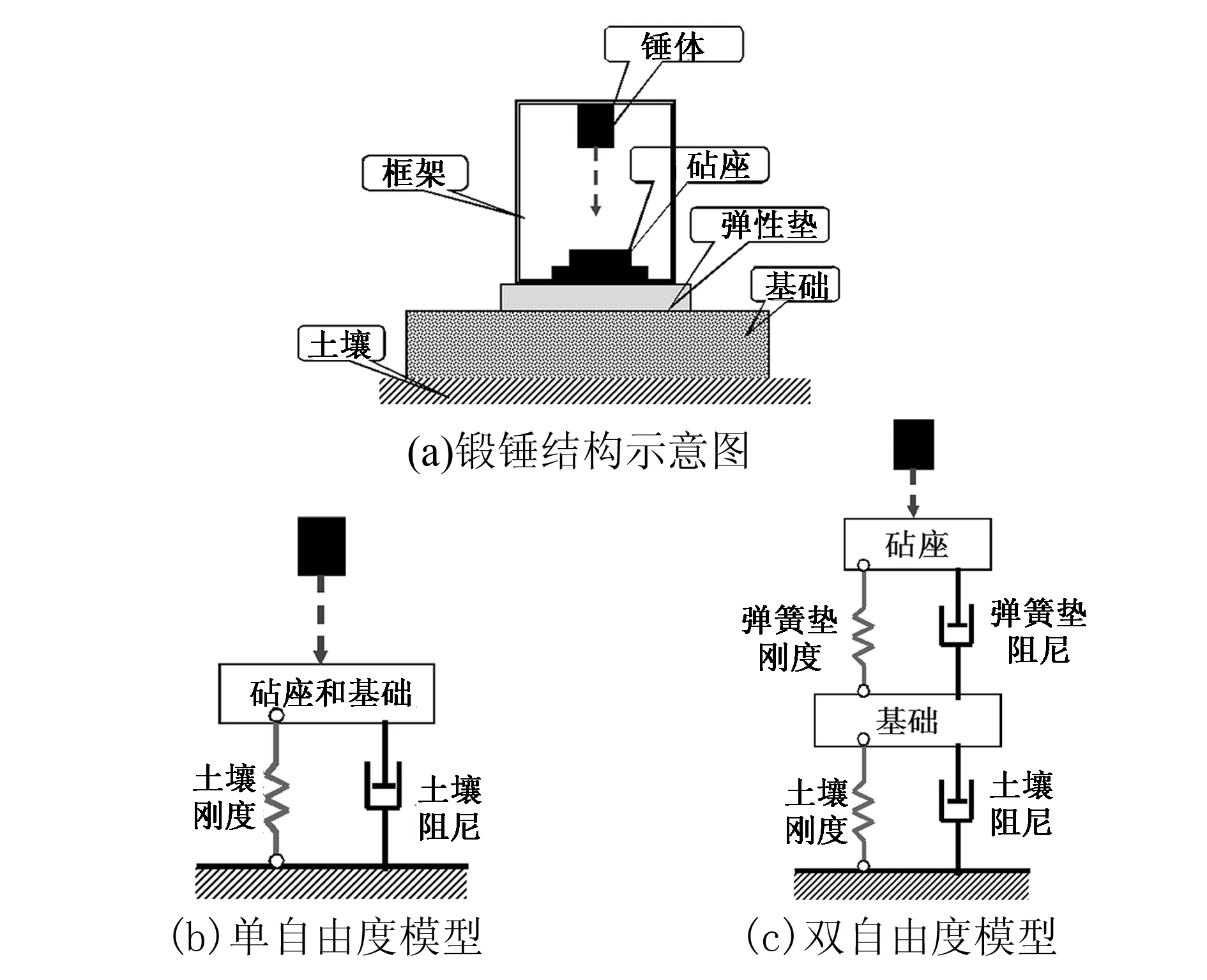
图1 锻锤振动模型分析

(二)抽象概念的形象化

主振型是多自由及连续系统振动的重要特性。对于低阶振动的振型，学生一般还可以想象，但对于高阶振动的振型，由于现实生活中较少见，学生难以想象结构还会跳出“优美的舞姿”。ANSYS，Abaqus等数值模拟软件都提供了结构模态分析的功能，利用这些软件可以给出结构各阶振动的模态[6]。如图2所示为一个10层的框架结构，由ANSYS模拟分析的3阶，4阶和5阶的模态，通过演示结构的振动模态，学生对高阶模态有了形象的映像。可以鼓励学生课下利用ANSYS或Abaqus对课本例题中简单结构的振动模态进行模拟，通过图形化的输出充分理解振动，模态的概念，让书中文字及数字的表达鲜活起来。

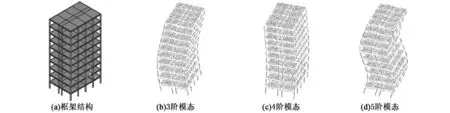
图2 框架结构的高阶模态

(三)基于MATLAB的仿真

MATLAB具有强大的计算仿真功能，也是工科专业常用的工具软件之一，它可以通过图形曲线的方式将课程中抽象的概念与结论形象的表现出来，便于学生理解。如在讲解单自由度振动时，位移、速度和加速度三者间的关系时，从公式中分析可知，位移，速度和加速度三者的幅值分别为A，ωA和ω2A，具有相同频率，相位上，速度超前位移90°,加速度超前位移180°,加速度始终与位移反向，可以利用MATLAB的图形输出，绘出三者随时间变化的曲线，如图3所示，结合曲线,将三者间的关系形象地反映出来。

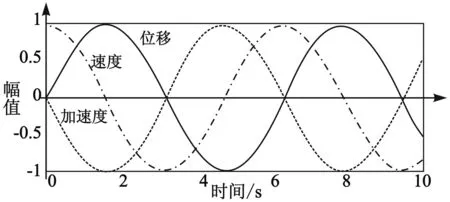
图3 位移、速度和加速度曲线

此外，MATLAB最重要的组件之一Simulink提供了一个动态系统(包括连续系统、离散系统和混合系统)建模、仿真和综合分析的集成环境。在该环境中，无需大量书写程序，通过简单直观的鼠标操作直接控制图形化的模块，就可构造出复杂的系统。图4所示为一个三自由度结构，在质量块m1上作用一简谐激励力P0sin(wt)，m1=m2=m3=m，其动力学方程为[7]：

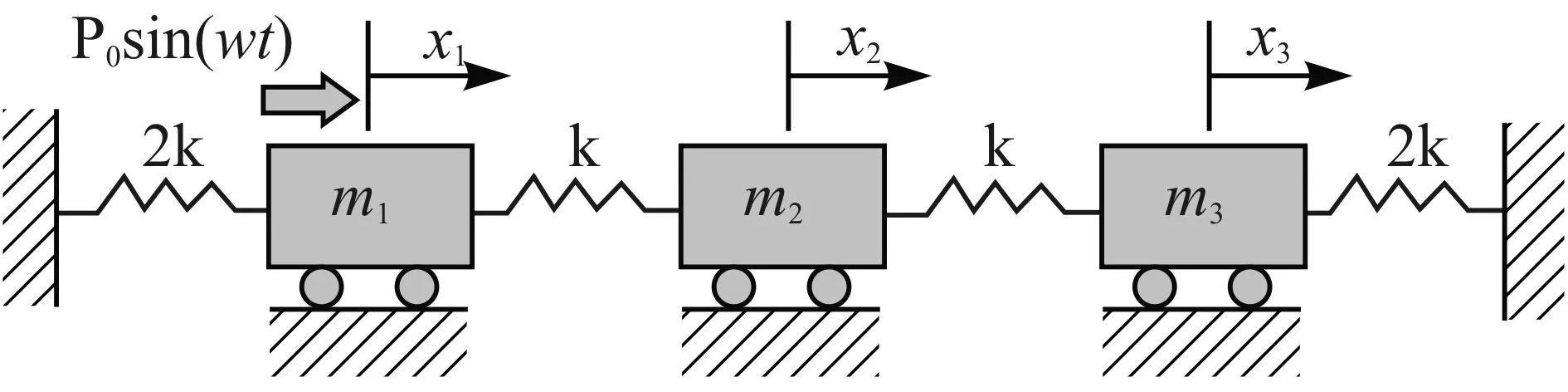
图4 三自由度结构

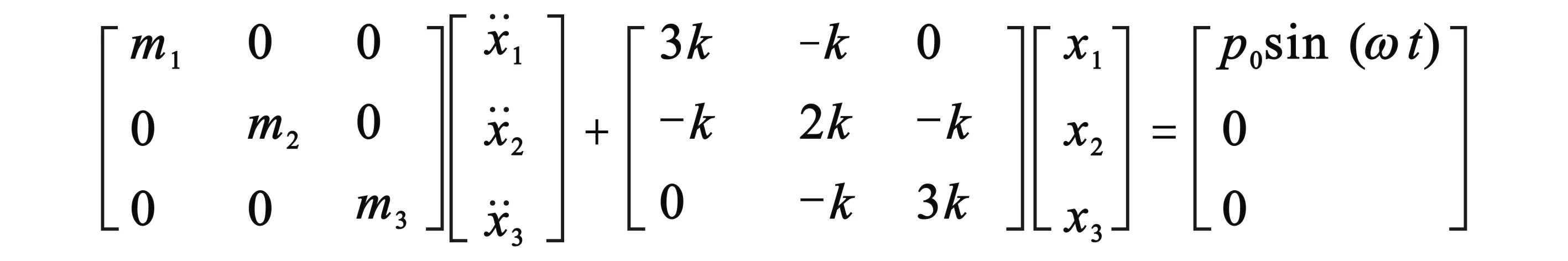
(1)

利用Simulink建立系统动态仿真模型，图5(a)所示为仿真模型功能框图，其含有正弦波模块、增益模块、减法模块、积分模块和示波器模块，由这些模块建立微分方程(1)的仿真模型。如m=1，k=1，P0=1，时间t取[0，50s]，ω分别取0.5rad/s、1.0 rad/s和1.7 rad/s运行仿真模型，由示波器模块输出系统的动态响应，如图5(b) ,(c)和(d) 所示。在整个仿真过程中，只需根据初始条件设定各个模块的参数，不用编写程序，易于学生上手。

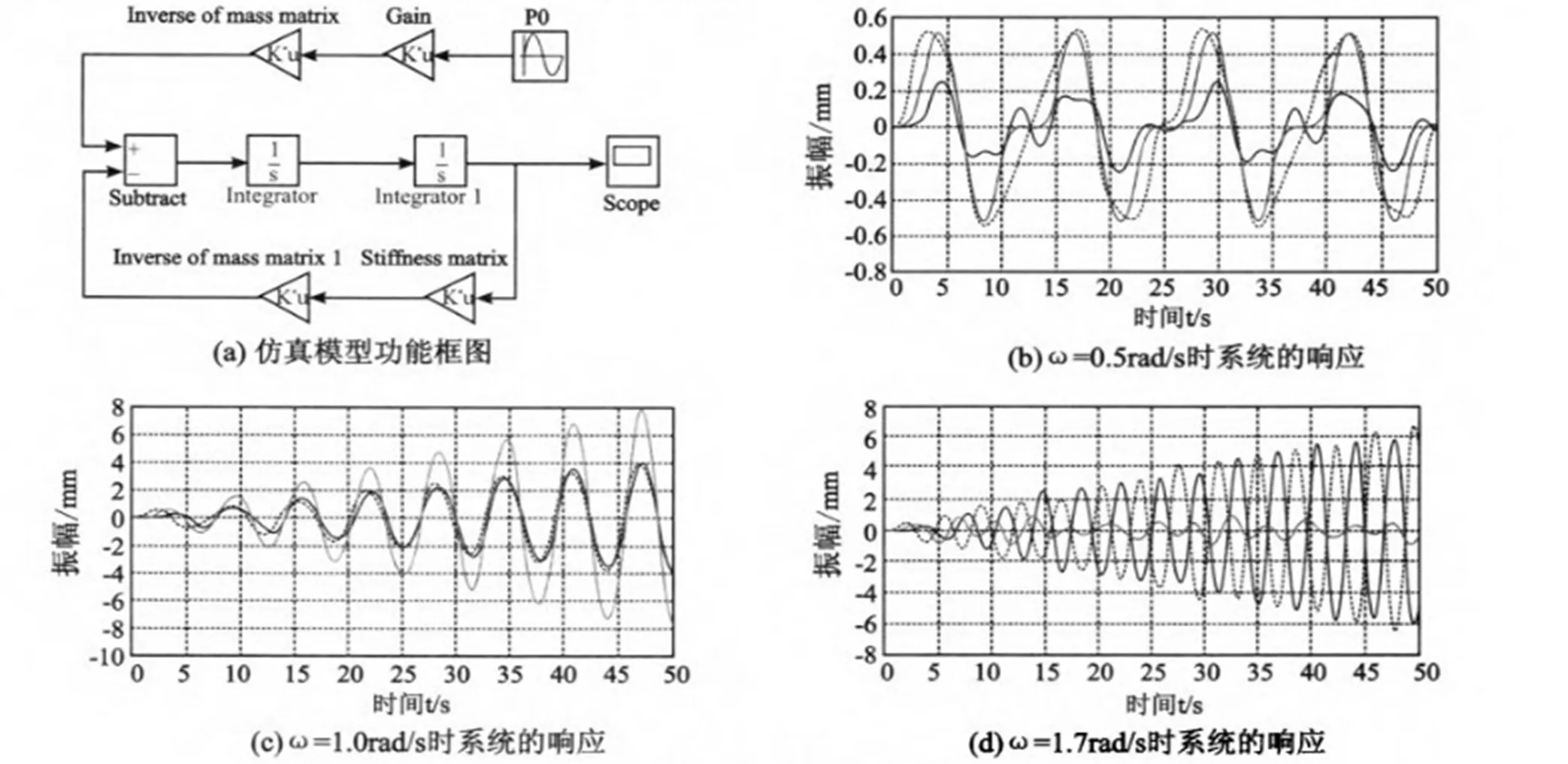
图5 系统动态仿真及在不同频率下的响应

通过上述两例来说明MATLAB在教学中的应用，引导学生用MATLAB对课程中的例题结果进行仿真，一方面对结果有形象化的理解，另一方面锻炼学生应用软件工具来帮助分析问题。

四、结语

通过形象化教学，在2013—2014学年第二学期振动力学课堂教学中，明显感觉学生学习的兴趣提高，主动借阅相关书籍阅读，课后提问也增多。之前学生在做课后作业时，对于一些简化的模型不理解，做题感到无从下手。由于形象化教学的引导，在这学期中，学生对模型的理解力提高，自学能力提高，作业质量明显好转。

振动力学课程由于是一门工程性很强的基础学科。在教学过程中，无论是工程实验还是模拟研究，可使用形象化教学的地方很多, 需要教师用心地去研究、开发。而对于应进行严谨推导的知识点，还是要用数学公式推导，再辅以形象的例子，帮助学生理解。充分利用多媒体教学方法，把传统黑板教学形式与多媒体教学手段相结合，激发学生的学习兴趣，培养学生分析问题的思路，引导学生自主的分析，归纳与总结，形成一个良好的学习习惯。

[1] 蔡国平.振动力学课程教学改革的几点思考[J].教育教学论坛，2010(35)：221-222.

[2] 曲淑英，王心健.力学课教学中形象化教学探索[J].电化教育研究，1999(4)：67-69.

[3] 高建纲，张泽，宋庆平，等.《高分子化学》形象化教学体系的设计与实践[J].高分子通报，2013(2)：94-98.

[4] 刘大年，史旺旺，孙贵根，等.“数字信号处理”课程的形象化教学方法探索[J].电气电子教学学报，2006，28(4):104-108.

[5] Singiresu S R.机械振动[M].李欣业,张明路,译.北京：清华大学出版社，2009.

[6] 何本国.ANSYS土木工程应用实例[M].北京：中国水利水电出版社，2011.

[7] 倪振华.振动力学[M].西安：西安交通大学出版社，1989.

(编辑：刘伟霄)

2014-06-08

中国矿业大学(北京)课程建设项目：“振动力学课程建设”(编号：K130602)。

毛灵涛(1974-)，新疆石河子人，博士，副教授，主要从事工程力学教学科研工作。

G40-057

A

1008-6927(2014)06-0076-04

DOI号：10.13320/j.cnki.jauhe.2014.0193