褪黑素时间序列中缺失值的填补方法研究
钱淑雯,李海燕,杨学智,李 慧,张尚尚,芦 煜,王京平,张治霞,徐 静
(北京中医药大学,北京 100029)
论 著
褪黑素时间序列中缺失值的填补方法研究
钱淑雯,李海燕,杨学智,李 慧,张尚尚,芦 煜,王京平,张治霞,徐 静
(北京中医药大学,北京 100029)

目的 模拟同一时间点数据完全缺失和部分缺失2种情况,通过填补值和实际值的对比,比较各填补方法对褪黑素(MT)时间序列的填补效果。方法 同一时间点完全缺失时,比较实际值与SPSS 5种填补方法填补结果;部分缺失时,除完全缺失的填补方法外,增加拟合时间序列模型填充。结果 完全缺失时,临近点的中位数和线性插值法的填补结果和两因素析因设计资料方差分析结果更接近于实际。实际值波动幅度较小的时候,插值法拟合效果好;在实际值波动较大时,临近中位数拟合效果好。部分缺失时,拟合模型填充效果好。结论 完全缺失时,如排除缺失值大幅波动,可以运用临近中位数和插值法对缺失值进行填充。在临近值波动幅度较小时,选用插值法填充值;在临近值波动幅度较大时,选用临近中位数填充值。部分缺失时,选用时间序列拟合模型填充。
时间序列;缺失值;填补方法
在中医药实验研究中,由于各种意外情况的发生,实验数据不可避免存在缺失的情况。在基于“天人相应”的时间序列数据分析时,缺失值的出现对时间序列统计分析极为不利。时间序列是某一个指标在不同时间上的不同数值按照时间的先后顺序排列而成的数列。缺失值的出现不仅影响各时间点的连接,对时间序列数据,序列太短会有损参数估计的稳健性,取较长序列则可以保证拟合模型的可靠性。而实际情形是,序列涵盖的历史值越长,序列中越有可能含有缺失数据,即使加强质量控制,也不能完全避免。褪黑素(MT)是“天人相应”研究中最常用的节律性指标,有强大的抗氧化能力,调节生物钟、保护小肠黏膜屏障、调节肠道细菌等广泛的生理作用[1]。MT分泌值正是这样一组典型的时间序列数据[2]。笔者以MT完整时间序列数为依据,创新地模拟同一时间点数据完全缺失和部分缺失2种情况,采用实际数据对比填补值的办法,结合两因素析因设计资料方差分析和时间序列图,比较各填补方法对MT时间序列的填补效果。
1 实验资料
1.1 动物及分组 192只健康SPF级昆明种(KM)雌性小鼠,体质量14~20 g,由北京维通利华实验动物技术有限公司提供。将192只雌性KM小鼠随机分为4组,每组48只:①正常明-暗周期组(Ⅰ组),在自然光条件下用普通饲料喂养;②正常明-暗周期+药物组(Ⅱ组),在自然光照条件下以含0.25%补肾方药(杞蓉益精颗粒)的饲料喂养;③异常明-暗周期组(Ⅲ组),使用电子定时器,每天18:00—24:00用日光灯光照6 h,普通饲料喂养;④异常明-暗周期+药物组(Ⅳ组),光照条件同Ⅲ组,以含0.25%补肾方药(杞蓉益精颗粒)的饲料喂养。
1.2 取材方法 为保证造模和取材的有效性,各组实验动物喂养30 d,造模时间相对较长。取材前4 h禁食,相近的时间点取材小鼠取自不同的饲养笼,尽量让小鼠处于各饲养状态,减少对指标的干扰。为细化MT的节律变化,充分反映变化趋势,取材于喂养结束后分别于次日2:00,4:00,6:00,8:00,10:00,12:00,14:00,16:00,18:00,20:00,22:00,24:00 12个时间点从小鼠眼眶后静脉丛取血,每个时间段(24 h)取12只测量,连续取4个时间段。所取血样经3 500 r/min离心15~20 min分离血清,所取血清置于带盖的锥形小管内于-70 ℃保存,用酶联免疫法测定其血清MT含量。
1.3 实验方法
1.3.1 模拟缺失方案 文献[3]研究表明,缺失比例在10%~30%时,各填补方法的填补结果较稳定,因此模拟缺失值确定为每个24 h周期内2个,缺失比例为16.7%,最接近稳定比例的平均值。运用EXCEL产生模拟缺失值的位置,以1~12的整数产生随机数。
1.3.2 完全缺失填补方案 如果在取材4个时间段中,每个24 h周期的同一时间点取材的数据都缺失时,鉴于SPSS软件医学研究中应用的普遍性,直接运用SPSS 18.0软件进行缺失值填补。鉴于该时间点的数据完全缺失,拟合的时间序列周期模型无该时间点的实验数据,因此不采用拟合的时间序列周期模型填补缺失值。比较各方法的填补值和实际值,结合两因素析因设计资料的方差分析和时间序列图,得出最优填补方法,并验证方法的合理性。①序列均值为取整列数据的均值;②临近点均值为去该缺失值临近的几个点的均值,具体几个点由附近点的跨度来设定;③临近点的中位数为取该缺失值邻近的几个点的中位数,具体几个点由附近点的跨度来设定;④线性插值法应用线性插值法填补缺失值,用该列数据缺失值前一个数据和后一个数据建立插值直线,然后用缺失点在线性插值函数的函数值填充该缺失值;⑤点处的线性趋势法应用缺失值所在的整个序列建立线性回归方程,然后用该回归方程在缺失点的预测值填充缺失值。
1.3.3 部分缺失填补方案 在取材4个时间段中,每个24 h周期的同一时间点取材的数据部分缺失时,除完全缺失填补方法外,根据MT周期分泌规律,以现有4组的实验数据拟合的时间序列周期模型[4],以周期模型值填充缺失值。
2 结 果
2.1 模拟缺失值位置 EXCEL随机产生1~12之间的整数,结果为3和9,确定24 h周期的第3个、第9个时间点为模拟缺失值位置,即4:00和16:00的实验数据缺失。
2.2 完全缺失各方法填补结果
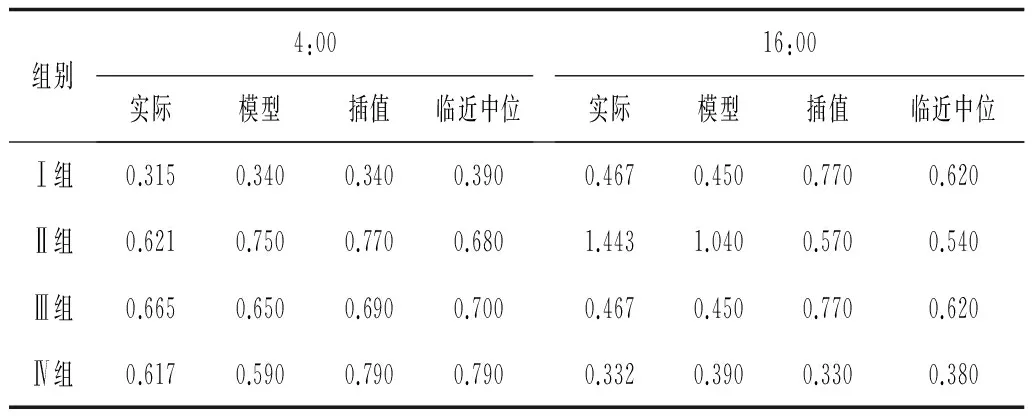
2.2.1 与实际数据对比 根据采集到的各实验组数据的情况,采用数据较全的Ⅳ组MT 4个24 h周期的时间段的时间序列数据,模拟在4个时间段的4:00和16:00数据都缺失。从4:00和16:00缺失数据的填补方法结果可以看出,临近点的中位数和线性插值法的填补值更接近于实际值。这两个时间点的实际值和SPSS 5种填补方法的填补结果见表1和表2。

表1 4:00 MT缺失数据的填补方法结果比较

表2 16:00 MT缺失数据的填补方法结果比较
2.2.2 填补结果的两因素析因设计资料方差分析 对Ⅳ组MT 4个时间段的数据进行两因素析因设计资料的方差分析,因素为额外光照和药物,额外光照有2个水平,“0”无额外光照,“1”表示有额外光照;药物有2个水平, “0”表示无药物,“1”表示有药物。分析在4:00和16:00,额外光照作用、药物作用和光照和药物交互作用对小鼠MT分泌是否有显著影响。见表3及表4。实际数据的方差分析结果显示额外光照作用对该时间点MT分泌无影响显著;药物作用对该时间点MT分泌有显著影响;光照与药物交互作用对该时间点MT分泌有显著影响。临近点的中位数和线性插值法的P值和显著性结果更接近于实际,但是存在与实际结果不一致的地方。因此,利用Ⅰ~Ⅲ组中较全的数据,进一步分析临近点的中位数和线性插值法适用的填补情形。见表3和表4。
2.2.3 各组填补前后的时间序列图 利用Ⅰ~Ⅲ组中较全的数据,进一步分析临近点的中位数和线性插值法适用的填补情形。采用时间序列图,分析临近点的中位数和线性插值法的适用范围,对比验证临近点的中位数和线性插值法的合理性。采用Ⅰ~Ⅲ组中一个周期内的各组较全的数据,模拟4:00和16:00的缺失值。结果显示,在实际值波动幅度较小的时候,插值法拟合效果好;在实际值波动时,临近中位数拟合效果好。缺失值填补方法不适用于临近点大幅度增大和减小的情况。见图1~3。

表3 4:00实际及缺失值填充结果方差分析

表4 16:00实际及缺失值填充结果方差分析
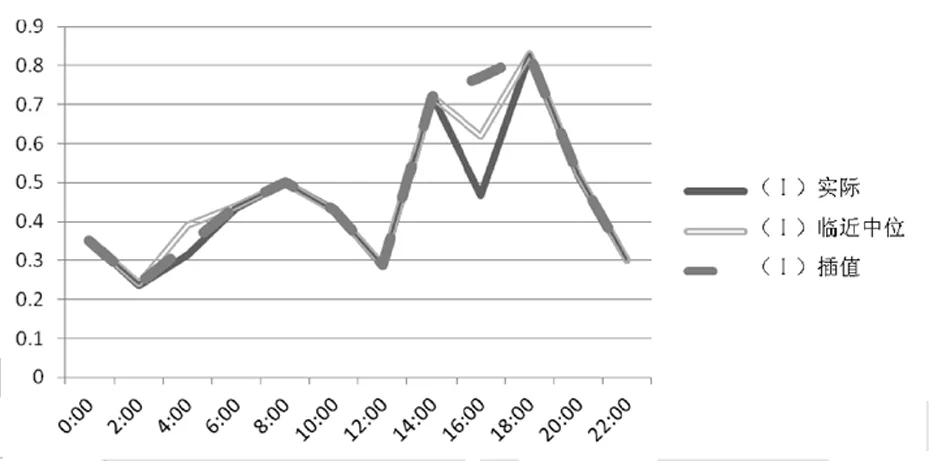
图1 Ⅰ组实际及缺失值填充的时间序列图

图2 Ⅱ组实际及缺失值填充的时间序列图
2.3 部分缺失各方法填补结果 由于各实验组第1个24 h时间段内MT时间序列数据较完整,模拟4组的第一时间段4:00和16:00缺失实验数据,拟合的时间序列周期模型,以周期模型值填充各组缺失值。从填补值来看,周期模型值填充效果较临近中位数和插值法好。见表5。

图3 Ⅲ组实际及缺失值填充的时间序列图
组别4:00实际模型插值临近中位16:00实际模型插值临近中位Ⅰ组0.3150.3400.3400.3900.4670.4500.7700.620Ⅱ组0.6210.7500.7700.6801.4431.0400.5700.540Ⅲ组0.6650.6500.6900.7000.4670.4500.7700.620Ⅳ组0.6170.5900.7900.7900.3320.3900.3300.380
3 讨 论
缺失按其产生机制可分为3类[5]:①MCAR完全随机缺失。此种缺失机制下,数据的缺失不依赖于要研究的因素,是随机的。②MAR随机缺失。随机是指条件随机,即在给定观察到的数据的情况下,缺失是一种随机现象,数据缺失的可能性只依赖于观察到的数据。③MNAR非随机缺失。此种情况下,数据缺失的可能性依赖于未观察到的变量。实验中时间序列数据缺失主要属于①②2种情形。
当数据存在缺失时,采用何种处理方法取决于数据缺失的特征,如若方法不适合数据,可能使得结果不可靠。现有研究中所采用的方法大致可分为以下几种:①完全集分析[6],存在缺失的观测将被剔除,仅有完整数据被用于分析。②单值填补,这种方法为每个缺失填补一个值,填补值可以是基于完整数据所计算的均值,也可能是根据完整数据拟合回归模型再基于回归模型的预测值做填补。③最大似然法,存在缺失数据时,似然法利用所观察到的信息得到参数的似然函数,进行参数估计。④多重填补[7],这种方法将缺失视为一种不确定性,在特定假设下,认为缺失的数据服从某种预测的概率分布;在填补时,每个缺失将被m个(m>l)从这个分布中所抽得的样本值所替代,这m个值之间的变异代表缺失所引入的不确定性。由于每个缺失被m个填补值所代替,所以最终会得到m个完整的数据集,填补之后的数据分析将基于这m个完整的数据集;每一个填补后得到的完整集都可以采用完整数据的分析方法进行分析。
在时间序列分析时,如果对缺失值采用简单剔除的处理方式,那么对试验结果的解释会产生影响数据的连续性、峰值的缺失、数据信息利用不充分等问题。对于时间序列数据,单个时间点数据缺失是较为常见的,单值填补是较为实用的。
研究结果显示,同一时间点取材的数据都缺失时,结合相关文献,能排除数据大幅变化,运用SPSS填补缺失值的方法有其意义。在排除时间序列缺失数据临近点大幅度增大和减小的情况下,可以运用临近中位数和插值法对缺失值进行填充。在临近值波动幅度较小的时候,选用插值法填充值;在临近值波动幅度较大的时候,选用临近中位数填充值。同一时间点取材的数据部分缺失时,建立时间序列模型拟合有很大意义,且同一时间点取材的数据部分缺失越少,拟合模型填充效果越好。但是本研究选用的填补方法相对简单,如果对缺失值填补要求很高,需选用数据挖掘中更精确的办法[8]。
目前尚未就缺失值处理方法达成广泛一致,尽管如此,在处理缺失值时,结合具体情形加以考虑。在相关文献中,缺失值的主要填补方法还有随机回归填补法、趋势得分法(PS)、马尔科夫链蒙特卡罗法(MCMC)和三次样条插值法等。
作为出现缺失值的后果,数据分析困难会随之发生,而且随着缺失值数量的增加,这种情况愈加严重。因此,尽可能避免缺失值的出现就显得极为重要,通过有效的设计最小化这种可能性,强化对数据的收集。如果是开创性的研究,相关文献基础较少时,应在执行实验过程中最低限度尽量减少缺失值。收集与研究目标绝对必要的数据,防止施加一个研究人员不必要的负担,提高收集的数据质量。适当的样本量估计,考虑实验中可能存在样本的丢失。设置预实验或参考相关文献,确定实验操作中可能发生的意外情况。提高实验人员的操作技能,规范实验操作,提高取材成功率。确定适合取材方法,保证指标科学性,提高取材成功率。防止样本的处理、保存和指标测量中可能发生的失误,提前进行实验培训。
[1] 高卉,阮明凤,龙浩成,等. 褪黑素对梗阻性黄疸大鼠小肠黏膜屏障保护作用的实验研究[J]. 现代中西医结合杂志,2007,16(8):1024-1025
[2] 徐静,冯前进,牛欣. 时间序列插值法在天人相应生物信号转导数据分析中的应用[J]. 中华中医药杂志,2012,29(4):895-899
[3] 高海威. 中医药临床研究中缺失数据处理方法探讨[D]. 广州中医药大学,2012
[4] 张熙,李济宾,张晋昕. 含有周期性的时间序列中随机型缺失数据的填补方法[J]. 中国卫生统计,2012,29(4):475-477
[5] Roderick JA Little,Donald B Rubin. 缺失数据统计分析[M]. 孙泽山,译. 北京:中国统计出版社,2004:4-10
[6] Deznjssje S,LaValley MP,Horton NJ,et al. Bias due to missing exposure Data using complete-case analysis in the Proportional hazards regression model[J]. Statisticsin Medieine,2003,22(4):545-557
[7] Schafer JL,Graham JW. Missing data:our view of the state of the art[J]. Psychol Methods,2002,7(2):147-177
[8] 陈光平. 基于时间序列数据特性的缺失值估计算法[J]. 计算机工程与应用,2012,48(12):135-138
Study on the method to fill missing values of melatonin time series
Qian Shuwen, Li Haiyan, Yang Xuezhi, Li Hui, Zhang Shangshang, Lu Yu, Wang Jingping, Zhang Zhixia, Xu Jing
(Beijing University of TCM, Beijing 100029, China)
Objective It is to simulate two cases of data completely missing and partially missing at the same time, and to compare the fill effect of melatonin (MT) time series of every method by comparing the fill value and the actual value. Methods In the case of data completely missing at the same time, five SPSS fill methods were used to fill the simulated missing values. Filling results were compared with the actual value. In the case of data partially missing at the same time, in addition to the completely missing filling methods, the time series model fitting was added to fill. Results In the case of data completely missing at the same time, median fill method of approaching points and linear interpolation results were closer to the actual value. Two-factor factorial design analysis of variance results were better. When the actual value had small fluctuations, the linear interpolation result was closer to the actual value. When the actual value had small fluctuations, the linear interpolation result was closer to the actual value. When the actual value had the larger fluctuations, the median fill method of approaching points result was closer to the actual value. In the case of data partially missing at the same time, the time series model fitting had the better result. Conclusion In the case of data completely missing, excluding the very large increase and decrease, median fill method of approaching points and linear interpolation can be used to fill missing values. When the actual value has small fluctuations, choose linear interpolation. When the actual value has the larger fluctuations, choose median fill method of approaching points. In the case of data partially missing, choose time series model to fill.
times series; missing value; fill method
钱淑雯,女,硕士研究生在读,研究方向为天人相应时间序列。
徐静,E-mail:xuj@bucm.edu.cn
北京中医药大学自主课题(2013-JYBZZ-JS-041);北京中医药大学自主课题(2014-JYBZZ-XS-031);北京中医药大学可获取的人体诊断信息关键技术创新团队(2011-CXTD-05)
10.3969/j.issn.1008-8849.2014.35.001
R-332
A
1008-8849(2014)35-3877-04
2014-05-30

