基于元胞自动机的无线网络安全态势模拟

陈剑锋，龙 恺，李明桂

(1.保密通信重点实验室，四川成都610041;2.中国电子科技集团公司第三十研究所，四川 成都610041)

0 引言

无线通信不受地理位置和空间限制，部署灵活，效率较高，近30年来一直是业界的研究和发展重点。无线网络通过无线通信技术将各类网元连接在一起，使信息传输摆脱了实体介质的束缚，用户可以通过移动通信网、广播网、Wifi、Wimax等多种手段接入网络，充分享受无线连接为生产、生活带来的便利。但是，无线网络天然的开放性特点也使得由病毒、木马等带来的安全问题较有线网络更为严重:各类恶意程序可能通过无线网络迅速传播，对无线节点、计算设备构成巨大的安全威胁，关键节点的失效可能会使整个无线网络瘫痪。

针对这类安全威胁，对恶意程序流行规律进行研究，建立风险的网络传播模型，形成无线安全态势的整体认知，是提升无线网络安全防御能力的关键因素。安全人员基于对态势的全面判断能够选择有效的响应措施，在最短时间内抑制威胁的扩散。元胞自动机［1］作为描述复杂动力系统的数学工具，已经在生物、工业、经济等多个研究领域得到了广泛应用，如利用元胞自动机作为Hash迭代函数［2］。由于无线网络中病毒传播过程的自相似性强、扩散较有规律，因而元胞自动机的特性使其能够对此类安全态势演化进行有效模拟。目前对病毒传播模型的研究均对客体状态及转移关系进行了定义，主要文献有ER复杂网络上的SIR模型［3］，SF复杂网络上的SIS模型［4］等。在元胞自动机与无线网络的结合方面，目前仅用于对拓扑结构等特征进行仿真［5］，而未涉及到对安全性质、安全态势进行验证的层面。

1 元胞自动机

1.1 定义

元胞自动机(CA，Cellular Automaton)也称为细胞自动机，起源于20世纪40年代，由“现代计算机之父”冯·诺依曼设计，是一类时间和空间都离散的动力系统。元胞自动机由规则网络(Lattice Grid)及附于其上的元胞(Cell)构成。每一元胞的状态均从同一集合中取值，遵循同样的转移规则，并在时刻变化时作同步更新。大量元胞在离散的时间片中，通过简单的相互作用而构成动态系统的演化［6］。

元胞自动机在设计时参照了生物现象的自繁殖原理，因此其概念和特征与一般的动力学模型不同。它不是由严格定义的物理方程或函数确定，而是一类模型的统称，这些模型由给定的规则构造，凡是满足这些规则的模型都可以视为是元胞自动机模型。

元胞自动机具有时间、空间、状态均离散的特征，即元胞只能取有限多个状态，只能在给定的空间中分布，且状态的变化需要等待时间点到来才可进行。这些性质导致其演化的规则在时间和空间上都具有局部性特征，元胞自动机的要素描述如下:

元胞:元胞是CA最基本的组成部分。元胞是不可拆分的变量，分布在离散的一维(线)、二维(面)或多维空间上;

状态:状态是一个有限集，可以是整数集，也可以是包含特殊意义的枚举集合;

元胞空间:元胞所分布的空间网格，一般都是有限的;

邻居:邻居是一个元胞的集合，由CA指定。由于CA演化规则的局部性特征，每一元胞状态更新时只需要知道其邻居元胞的状态即可;

规则:根据中心元胞及邻居的当前状态确定下一时刻中心元胞状态的动力学函数;

时间:CA在时间维的变化是离散的，时间t是一个非负整数值，而且连续等间距。时间具有顺序性，t与t+1时刻的CA状态具有因果关系。

元胞自动机在定义了基本元素后可自动运行，元胞状态随着时间的推移将不断变化，整体上呈现出有规律、或者杂乱的特征。元胞自动机分类的研究是元胞自动机的一个重要的研究课题和核心理论，Wolfram将所有元胞自动机的动力学行为归纳为四大类［7］:

1)平稳型:自任何初始状态开始，经过一定时间运行后，元胞空间趋于一个平稳的构形。

2)周期型:经过一定时间运行后，元胞空间趋于一系列简单的周期结构。

3)混沌型:自任何初始状态开始，经过一定时间运行后，元胞自动机整体表现出混沌的非周期行为，通常表现为分形分维特征。

4)复杂型:出现复杂的局部结构，或者混沌状态，有时会传播至其它区域中。

使用形式语言描述，CA可以定义为四元组CA=(Ld，S，N，f)，其中 CA 代表元胞自动机系统，Ld代表一个规则划分的d维网络空间(d为正整数，一般取1或2，代表一维或二维空间)，S为元胞状态取值的离散有限集合，N代表单个元胞的邻域内元胞状态的组合(邻域包括中心元胞及邻居元胞):假设中心元胞的邻居个数为 j，则 N=(S0，S1，…，Sj)。令St+1i这种表示方式代表元胞i在t+1时刻的状态，则f是将St+1i映射为S上的一个转换函数，又称为局部规则或状态转换函数。元胞i在t+1时刻的状态取值将取决于t时刻元胞i自身及所有邻居的状态组合，即

1.2 演化规则

元胞自动机算法是一种简单、但描述能力强大的数学算法，在元胞自动机中各个相邻元胞一般存在着交互作用关系，在系统运行开始以后每个元胞的状态都是整个系统在一些规则作用下不断进化的结果。只要不断地重复应用这些规则，就可以用元胞自动机的演化进程来预测系统将来的发展情况，在系统停机后将演化结果重新代入现实语义中，即可得到研究者们所关注的程序结果。

CA的核心是状态定义及规则描述，在状态基本固定的前提下，对规则的微小修改都可能导致最终结果的显著变化，因此规则制订必须严谨、能够切实反映现实系统的运行状态。CA中的每一个元胞在下一时刻的状态完全由自身及邻居当前的状态决定，因而邻居的范围决定了规则的定义域。根据元胞自动机网络的维数不同、半径选取不同，邻域的范围也有所不同。图1所示分别为一维、二维元胞自动机中以中心元胞为基准的邻域元胞示意图，图中r表示邻域半径。

图1 中心元胞邻居定义Fig.1 Definition of central cell neighbor

在CA的一次演化过程中，所有元胞都会逐一被作为中心元胞参与运算，根据运算的结果执行下一步的状态转移。这种状态转移是全局同步进行的，即各个元胞的状态变化没有先后顺序，在时间推进到t+1的瞬间，所有的元胞都将转移至新的状态，这也是经典CA的状态转移方式。中心元胞这种转移的确定性使对于相同的起始状态而言，该CA的每次运行结果都是一样的，不能将随机性这类反映现实系统运行的因素在模型中体现。

为了进一步增强CA的适用性从而能描述更复杂的动力系统，研究者们引入了概率CA，在这类CA中元胞下一时刻的状态不仅依赖邻域元胞，还取决于一个概率p，演化规则将根据p的取值进行分支，从而使元胞在下一时间进入一个服从概率分布、不可预知的状态。即:

其中，0≤p≤1，P1，P2，…，Pn均为［0，1］上的区间，∪Pi=［0，1］且对于不同的 i，j都有 Pi∩Pj= ∅。即p必定会落入转换函数f的一个子项中，中心元胞的下一状态将由此子项计算并唯一确定。另外，CA所在网络空间通常是有限的，因此状态转移函数在处理边界元胞时会出现输入取值不足的情形，一般CA在建立时就指定了边界问题的处理方式，这里将缺失的元胞状态都视为缺省状态。

2 无线网络安全态势模型

2.1 构建目标

这里研究的对象无线网络是由大量分布在不同位置上的主机(或智能设备、传感器)通过无线方式彼此连接构成的自组织网络，节点间通过访问点间接连接，或直接以点对点方式相连。相对于固定网络，这类无线网络(包括无线传感器网络WSN，或自治无线网络)具有地理位置分散、信息交互需要经过多跳、以自动管理为主、人工干预较少的特点。为方便研究，这里略去各计算单元在结构与功能上的差异，将它们作为彼此相同的元胞，将目标无线网络映射至平坦的二维网格中，网格中每一小格代表元胞。构建的CA使用Von Neumann型邻居定义，取r=1，即只有直接相邻的两个节点才被认为具有连接关系。

元胞的状态集{Su，Id，In，De，Sr}为各节点相对于某一网络威胁(病毒、木马等)的安全状态，元胞在某一时刻只能处于这五种状态中的一种，状态空间定义如下:

Su(Susceptive):节点尚未被威胁感染，但易受感染;

In(Infected):节点已被感染，但系统尚能执行操作，处于该状态的节点会传染邻居节点;

Im(Immune):节点对威胁处于免疫状态，不会被感染。此类节点有一定几率升级为Sr节点;

Id(Idle):节点被感染，且系统无法执行任何操作，可视为当机。当机的节点会以很小机率由管理者重启而恢复为In状态;

Sr(Serve):安全服务类节点，对威胁免疫，且能为已感染的邻居节点清除威胁。

状态间的转换关系如图2所示。称某时刻网络中元胞状态的分布为一个格局，代表无线网络在某时刻的安全态势。随着时间的推移，格局也在不断演变，直至满足预先设置的停机条件使自动机终止运行。威胁出现前大部分元胞的默认状态为Su态，威胁的出现会使少数节点进入In态，而后安全专家设计、部署了防御工具将一些节点转入Sr态。在格局变化的过程中In节点会感染附近的正常节点，而Sr节点会治愈附近的感染节点，格局的变化直接反映了无线网络当前的安全态势。

图2 CA状态间的转换关系Fig.2 Transition relation between CA states

2.2 演化规则

令感染率ri表示状态为Su的元胞受附近一个In态元胞影响，下一时刻被感染的概率;治愈率rh表示状态为In的元胞受附近一个Sr态元胞影响，下一时刻被治愈的概率;致死率rd表示状态为In的元胞下一时刻进入当机状态的概率;转变率rs为状态为Im的节点转变为具有清除能力节点态Sr的概率;重启率re为一个当机节点进行重新启动并进入In节点的概率。为表述方便，计算中心元胞邻居中In态元胞数量为a，Sr态元胞数量为b，则CA元胞状态演化规则矩阵如表1所示，表中首行为前一时刻的状态，首列为后一时刻的状态，状态交叉处的取值为状态间转移的概率。

表1 元胞状态演化规则Table 1 Evolution rules between CA states

在CA定义时，需要仔细选择ri、rh等参数的取值，确保表中概率不会落在合规区间之外。

2.3 属性断言

给定了起始格局和演化规则，元胞自动机就可以一直运行下去。然而，受概率事件的影响，每一次格局的变化都不会完全相同，而仅仅是遵循一定的内在规律。为了捕捉这类规律，可以用属性断言来建立对格局特点的描述，在CA运行中通过断言的证实或证伪来确定与规律的符合度。

属性断言按对象的范围分为全局属性断言、局部属性断言等。一项属性断言代表一条待验证的性质，按性质是否在给定格局里成立，属性断言的取值为true或false。例如，在时刻t对应的某一格局c中，全局属性断言“当机节点的个数占总节点的20%以上”可以描述为P1=Eval(Countt=tcc({Id})＞20%)，其中Eval算子检验属性表达式的值，其返回值为真或假;Count算子统计格局中某一状态元胞的数量。这条属性断言反映了系统的整体安全状态。

局部属性断言仅关心少部分元胞的状态，如“指定节点x在30个时间周期后处于免疫状态”可以描述为 P2=Eval(Nextt=30x∈{Im，Sr})，Next算子表示返回元胞在给定时间间隔后的状态。该属性断言可以用来表达对于关键节点状态的验证目标。

在同一初始格局的多次试验中，属性断言的总体满足情况无法用单一true或false表示，而是呈现出一种倾向性。约定如果总计进行m次试验，满足属性的格局出现了n次，则属性断言的满足率为100%×n/m，随着试验进行的次数增多，该值通常都会收敛至一定范围内。

3 基于CA的态势模拟

3.1 起始条件

为模拟现实中无线网络安全态势的演变情况，这里设计三类格局场景，即威胁入侵场景，威胁抑制场景和安全对峙场景。

如图3所示，威胁入侵场景主要用于模拟威胁的蔓延，起初恶意代码只在网络的几个分散节点出现，随后逐渐随时间而扩散;威胁抑制场景模拟大量免疫节点对少部分感染节点的威胁清除过程;安全对峙场景模拟在威胁爆发一段时间后，安全节点与受感染节点之间的对峙情况，期望得到最终元胞状态的分布。

如图3所示，在一个32×32元胞的网格上对上述场景进行模拟试验，在时间流逝到指定条件时终止，各场景期望验证的属性如下:

威胁入侵场景:初始分布如图3(a)所示，经过30个时间单位以后，计算网络内感染节点是否超过40%;

威胁抑制场景:初始分布如图3(b)所示，经过40个时间单位以后，计算网络内受感染节点数量是否少于20;

安全对峙场景:初始分布如图3(c)所示，经过30个时间单位以后，计算当机或受感染节点数量少于已免疫节点;

同时，对各变化率进行量化赋值，取ri=rh=0.

3.2 算法实现

在CA 中进行属性验证一般使用重复迭代的方法，每一次迭代意味着时间推移了一个单位。算法持续运行，在终止条件达到后计算属性的满足情况，并给出最终结果。基于这种思想，算法实现的伪代码如下:

图3 不同态势模拟场景的初始分布Fig.3 Initial distribution for different types of simulation scenario

3.3 实验结果分析

取试验次数n=20，在一台配置为i3 CPU，内存为4096MB的计算机上运行自制的VS 2010 C#元胞自动机模拟程序，将试验结果叠加至同一坐标系，得到试验结果如图4、图5和图6所示，模拟试验结果的横轴为迭代次数，纵轴为处于不同状态的节点数量，“○”指代当机或受感染节点数量，“×”指代已免疫节点数量。

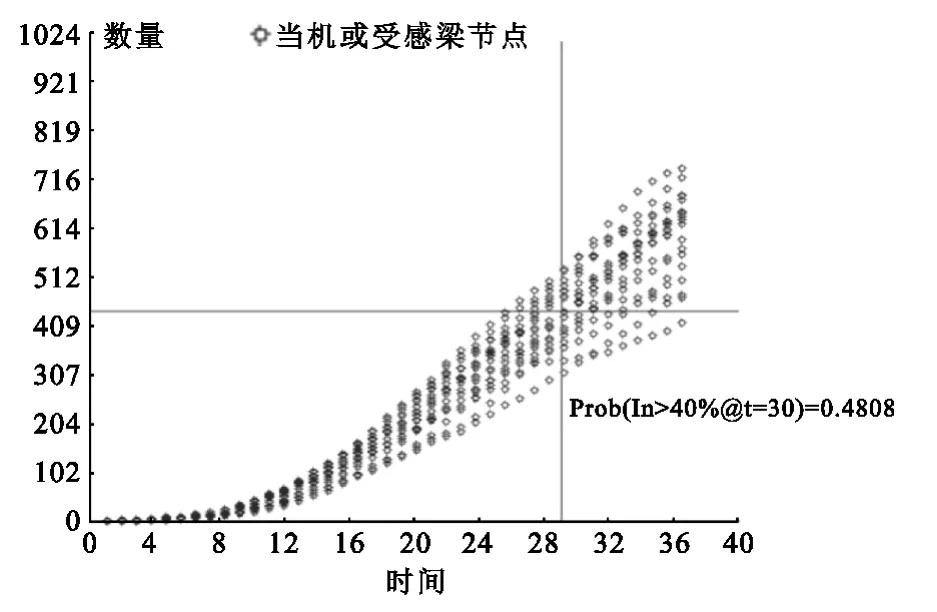
图4 威胁入侵场景模拟试验结果Fig.4 Result of threat intrusion situation simulation

将试验结果对照属性断言可以认定:在威胁入侵场景图4中，经过30个时间单位以后网络内感染节点超过40%的几率为0.48;在威胁抵制场景图5中，网络内受感染节点数量在上升至极大值后随之降低，经过40个时间单位以后网络内受感染节点数量少于20的几率为0.45;在安全对峙场景图6中，免疫节点与受感染节点数量均呈上升趋势，但免疫节点增加速度更快。经过30个时间单位以后当机或受感染节点数量少于已免疫节点的几率为0.68。

图5 威胁抑制场景模拟试验结果Fig.5 Result of threat suppression situation simulation

图6 安全对峙场景模拟试验结果Fig.6 Result of security confrontation situation simulation

4 结语

无线网络在提供部署灵活、使用方便等优点的同时也延续了有线网络固有的安全问题，病毒等恶意程序将会为无线网元带来较严重的安全威胁。元胞自动机作为一类具有严格理论基础的数学模型，能够对无线网络信息传播过程进行模拟，进而应用于无线网络安全态势展现和评估环节中。文中建立了无线网络的概率元胞自动机模型，给出了系统内威胁蔓延、治愈恢复等行为的形式化描述。基于预定义的属性断言，通过模型运行得到的验证结果可为无线网络安全态势分析及事件响应提供有效的决策支撑。

［1］ HALPERN P.A Guide to Structurally Dynamic Cellular Automata［J］.Am.J.Phys，2003，57(05):28 －39.

［2］ 张传武.基于细胞自动机的Hash函数方法［J］.通信技术，2010，43(12):123 －125.ZHANG Chuan － wu.Hash Function based on Cellular Automata.Communications Technology［J］.2010，43(12):123－125.

［3］ 于鑫，段晓东，刘向东，等.基于元胞自动机的流行病传播模型及模拟［J］.计算机工程与应用，2005(02):205－209.YU Xin，DUAN Xiao － dong，LIU Xiang － dong，et al.Cellular Automata Model to Simulate the Infectof the Epidemic Diseases［J］.Computer Engineering and Applications.2005(02):205 － 209.

［4］ BARABáSIA L，ALBERTR.Emergence of Scaling in Random Networks［J］.Science，1999，286(5439):509 －512.

［5］ Stavros Athanassopoulos，Christos Kaklamanis，Gerasimos Kalfountzos，et al.Cellular Automata for Topology Control in Wireless Sensor Networks［C］//Electrotechnical Conference(MELECON)，2012 16th IEEE Mediterranean.Berlin，Germany:IEEE，2012:212 －215.

［6］ CULIK K，HURD LP.Formal Languagesand Global Cellular Automaton Behavior［J］.Physical D，1990(45):396 －403.

［7］ WOLFRAM S.Cellular Automata as Models of Complexity［J］.Nature，1984，311(06):419 －424.

［8］ SONG Yu － rong，JIANG Guo－ Ping.Modeling Malware Propagation in Wireless Networks using Cellular Automata［C］//Neural Networks and Signal Processing，2008 International Conference.Piscataway，NJ:IEEE，2008:623 －627.