一种改进的极化码置信译码器

张青双，刘爱军

(解放军理工大学通信工程学院，江苏南京210007)

0 引言

极化码是第一种在二进制对称信道(BSC)条件下被证明能够达到香农极限的信道编码方式，并且具有较低的编译码复杂度［1］。Arikan在2009年提出极化码的概念以后，在编码领域引起巨大反响。然而极化码的连续抵消(SC)译码算法并不能达到理论上的达到香农极限误码性能，为了进一步挖掘极化码的性能极限，许多高性能的译码算法被相继提出。

序列SC译码(SCL)［2］，采用堆栈的 SC译码(SCS)［3］以及 CRC 辅助的 SCL 译码［4］是基于 SC 译码的改进型算法，能够带来很大的误码性能提升。特别是CRC辅助的SCL算法，在码长达到2 048时误码性能能够超过部分Turbo码。然而，上述的算法都是串行译码，译码输出效率低，译码复杂度高，限制了其在高速通信系统中的应用。置信译码(BP)在LDPC译码过程中得到成功的应用，同样可以用于极化码的译码［1］。文献［5］给出的结果显示，BP译码能够在低译码延迟的条件下获得比部分SC译码改进算法更好的性能。

文中提出了一种极化码BP译码的改进算法，旨在进一步提升其译码性能。在极化码的编码因子图中，节点被分为两种:确定节点和信息节点［6］。确定节点承载的是已知的比特信息，相应的它的先验信息也为已知;信息节点承载的是未知的比特信息。因子图中的四个节点形成一个计算单元，每一个节点的似然信息都可以通过其他三个节点计算得到。在译码迭代的过程中，当确定节点的似然信息计算错误时，可以对其他三个节点的似然信息做一定的修正。文中给出了一种修正算法，即通过引入一个修正参数对其他三个节点似然信息进行修正以提高似然信息的可信度。然后，利用高斯近似的思想，给出了一种修正参数的计算方法。仿真结果表明，该修正算法能够在牺牲很小复杂度的条件下获得0.2 dB左右的性能提升。

文中主要介绍了极化码的构造，对数域的BP译码算法，改进的BP算法(MBP)以及采用高斯近似的修正参数计算方法。最后给出了加性高斯白噪声信道(AWGN)条件下的仿真结果以及算法复杂度分析。

1 极化码

1.1 极化码的编码

极化码是利用信道极化现象提出的信道编码方式，最早由Arikan发现并提出［1］。基于信道组合和分离的理论，N个二进制离散无记忆信道(BDMC)通过模二加的方式组合在一起然后分离后［7］，当N趋于无穷大时，部分信道的信道容量会趋近于1，相应的其他信道的信道容量趋近于0。利用容量较大的子信道传输有用信息，剩下的子信道传输确定信息，由此可以形成极化码。极化码由三个参数确定:码长N=2m，m＞0，码率R=K/N以及一个K维的子集Aa⊂{1，2，…，N}。Aa表示用于传输信息的子信道的序号，在AWGN信道条件下，可以利用密度进化的方式确定［8］。假设=(u1，u2，…，uN)是编码前的比特组，则由子集Aa确定的的子矢量uAa是需要传输的比特信息，而Aa的补集Ac确定的子矢量uAc为确定的0或1信息组，这样编码后的码字可以表示为:

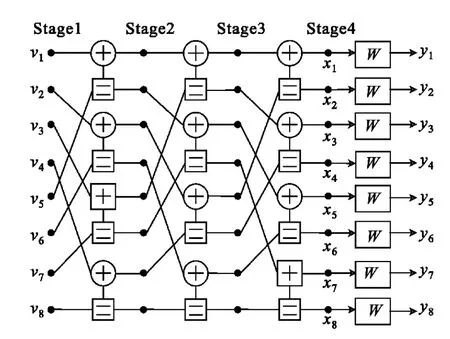
图1 N=8的极化码编码因子Fig.1 Factor graph for polar codeswith N=8

1.2 极化码的对数域BP译码

考虑到LDPC的BP译码算法是基于其二分图，极化码的BP译码算法的似然信息传递方式可以由其因子图导出。考虑码长N=2m，m＞0的极化码，其因子图共有(m+1)×N个节点，每四个节点形成一个基本计算单元(PE)。设整数对(i，j)，0≤i≤m+1，1≤j≤N 表示第 i层(stage)的第 j个节点，则每一个PE(Process Element)中四个节点似然信息传播方式如图2所示。

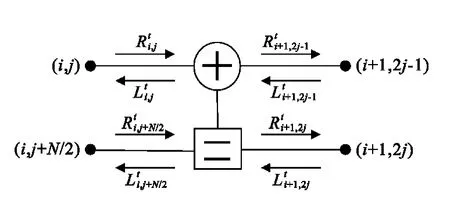
图2 BP译码的基本处理单元Fig.2 Basic PE for BP decoding

信息，t为迭代次数，其定义为

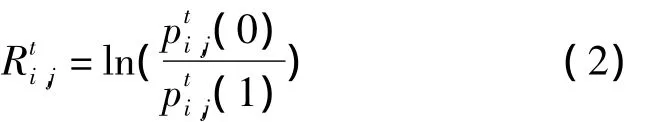
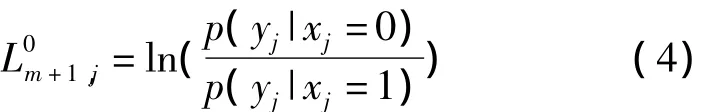
代过程中，对数似然信息的更新过程为［7］:

式中，f(x，y)=2a tan h(tan h(x/2)·tan h(y/2))。当迭代次数t达到给定的迭代阈值m Iter时，完成译码输出。

发送的信息比特可以由子集Aa⊂{1，2，…，N}确定。

2 修正的BP算法

2.1 似然信息修正

图3给出了N=8的因子图中四种不同的PE，圆形节点为信息节点，方形节点为确定节点。根据输入节点类型的不同，因子图包含四种不同的PE。一般的BP算法除了在初始化的时候，对不同类型的节点赋予的初值不同，译码过程中不会考虑到因子图中节点的差异性，这样就会丢失部分有用的信息。修正算法正是基于节点的差异性而提出来的。

由图3可以看到，可以根据PE的输入节点的类型将其分为4类，分别表示为(a)、(b)、(c)、(d)。对于PE(a)，输入节点均为确定节点，如果其对数似然信息计算错误，不会对译码结果造成影响，因此不需要对其做任何的修正。对于PE(d)，两输入节点均为信息节点，似然信息的对错无法判断，对其同样不做任何修正。

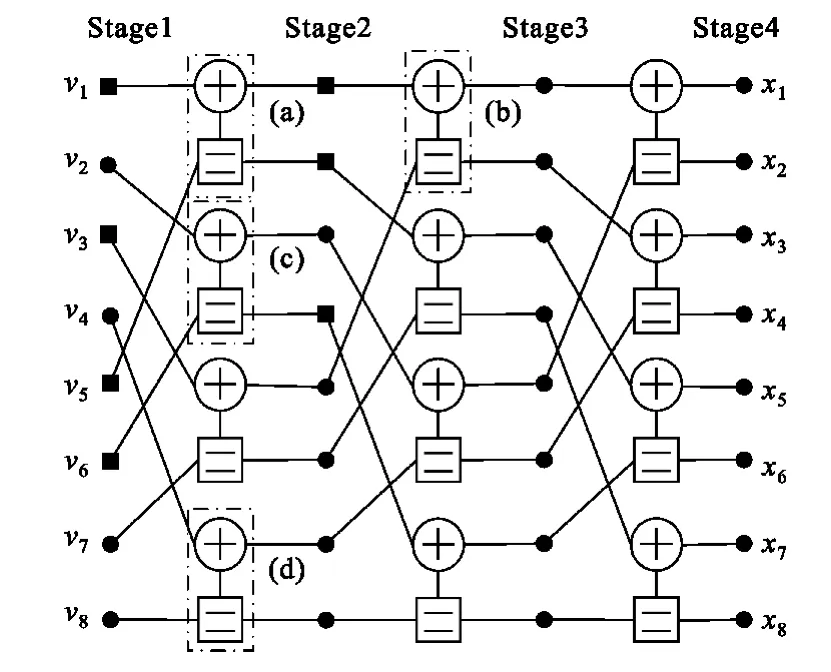
图3 因子图中四种不同的PEFig.3 Four different PEs in factor graph

对于PE(b)、PE(c)，一个输入节点为确定节点，另一个为信息节点。在迭代译码的过程中，当确定节点的似然信息计算错误时，错误必然来源于其他三个节点的似然信息。对其他三个节点的似然信息做一定量的修正，然后重新计算信息节点的似然信息，这样可以一定程度上提高信息节点似然信息的可信度。考虑此种类型PE的两输入节点为确定节点(i，j)和信息节点(i，j+N/2)，如果被错误计算，则进行如下修正:

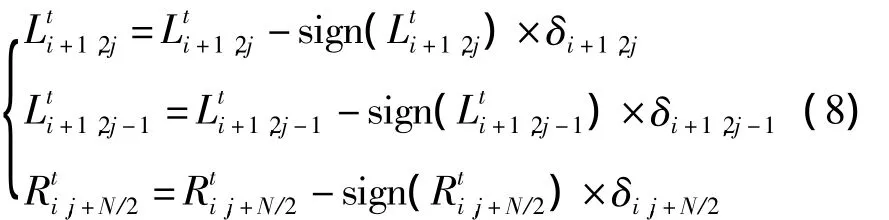
2.2 参数选择的高斯近似算法

只有合理的参数选择才会带来误码性能的提升。很显然，过大的修正参数会带来性能更大的恶化，而太小的值又不会有足够的效果，文中考虑采用高斯近似的方法给出一组修正参数。

在AWGN信道条件下，接受信息的对数似然信息为均值为 2/σ2，方差为 4/σ2的高斯分布，σ2为信道的噪声方差。这样，根据高斯近似的思想的分布可以近似为高斯分布，设其均值为，1≤i≤m+1，1≤j≤N。根据文献［9 － 10］可以利用递归计算得到

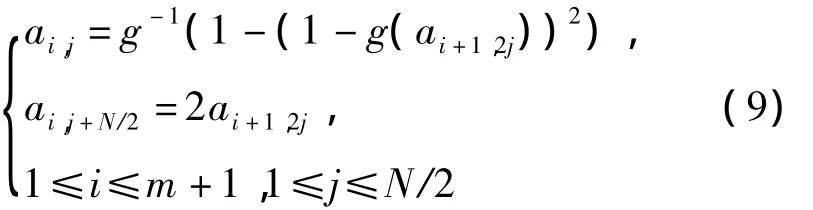
式中，截止条件为 am+1，k=2/σ2，k=1，2，…，N。函数g(x)具有如下形式:

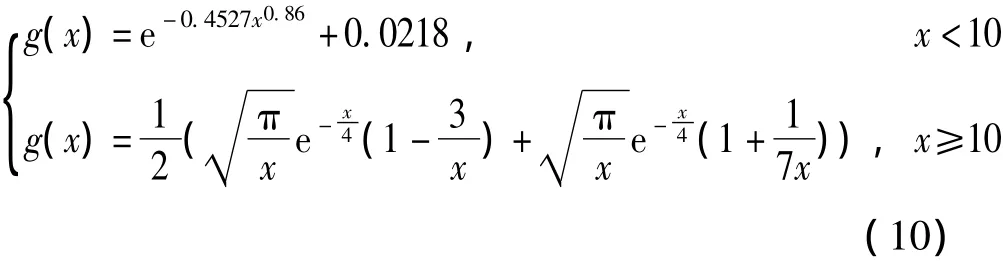
式中，pe表示发生错误的概率，本算法中假设三个对数似然信息错误的概率相等为1/3。Ee［Lti，j］表示发生错误条件下的条件均值。利用高斯分布的特性，可以得到

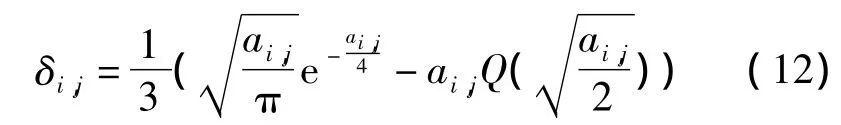
3 数值分析

3.1 复杂度分析

在工程实现的过程中，函数tan h(x)和a tan h(x)可以用查表的方式实现。根据式(5)，每一个对数似然信息的更新需要1次加法，1次乘法和3次查表。每一个PE需要四次似然信息的更新。对于码长为N=2m，m＞0的极化码，因子图包含m×个PE，每次迭代过程则需要m××4次加法，m××4次乘法以及 m ××12次查表。

修正的BP算法会带来额外的复杂度。根据式(8)，每次修正需要3次加法，修正以后还需要重新计算。假设所有确定节点的似然信息都计算错误，表1给出了不同码长，码率为1/2的条件下，每次迭代BP和修正的BP算法复杂度数值。其中加法用‘+’表示，乘法用‘*’表示，查表用‘LUT’表示。从表1中可以看出，修正算法带来的额外复杂度与原复杂度的比值分别不会超过17.86%、7.14%、7.14%，且随着码长的增加逐渐递减。

表1 不同码长复杂度对比Table 1 Computation complexity for different block lengths

3.2 性能仿真

为了验证修正的BP译码算法的性能，下面给出了AWGN信道条件下的误码率Monte Carto仿真，码率为 1/2，码长分别为 128，256，512，迭代次数为50。编码方式采用文献［1］的方式，译码分别为对数域BP算法和修正的BP算法。图4给出了两种算法的误码性能对比，可以看出在相同误码率条件下，修正算法能够带来0.2 dB左右的比特信噪比的提升。因此，修正的算法能够在牺牲少量复杂度条件下换取较好的性能。

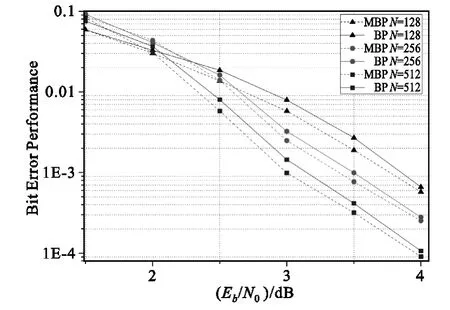
图4 BP及其修正算法误码率曲线Fig.4 Bit error rate curve for BP and MBP with different block lengths

4 结语

文中提出了一种极化码对数域BP译码的修正算法，通过对错误计算的对数似然信息进行修正以提升译码性能。在修正参数的选择上，运用了密度进化的高斯近似思想，通过把对数似然信息近似为高斯分布来获得一个合理的修正参数。仿真结果表明，修正的BP算法能够在复杂度少量增加的情况下改善0.2 dB左右的误码性能。虽然性能提升不大，希望这种修正的思想能够给后来的研究者一些启发，找到性能更加优异的极化码译码算法。

［1］ ARIKAN E.Channel Polarization:a Method for Constructing Capacity Achieving Codes for Symmetric Binary－input Memoryless Channels［J］.IEEE Trans.Inf.Theory，2009，55(07):3051 －3073.

［2］ TAL I，VARDY A.List Decoding of Polar Codes［C］//Proc.2011 IEEE Int.Symp.Inform.Theory.St.Petersburg:［s.n.］，2011:1 －5.

［3］ CHEN K，NIU K，LIN JR.Improved Successive Cancellation Decoding of Polar Codes［J］.IEEE Trans.Comm.2013，61(08):3100 －3107.

［4］ NIU K，CHEN K.CRC －Aided Decoding of Polar Codes［J］.IEEE Communication Letters，2012，16(10):1668 －1671.

［5］ HUSSAMIN，KORADA S，URBANKE R.Performance of Polar Codes for Channel and Source Coding［C］//IEEE International Symposium on Information Theory，2009.Seoul，South Korea:IEEE，2009:1493 －1495.

［6］ ALPTEKIN P.An FPGA Implementation Architecture for Decoding of Polar Codes［C］//International Symposium on Wireless Communication Systems(ISWCS2011).Aachen，Germany:［s.n.］，2011:437 －441.

［7］ 李斌，王学东，王继伟.极化码原理及应用［J］.通信技术 2012，45(10):21 －23.LIBin，WANG Xue－dong，WANG Ji－wei.Theory and Application of Polar Code［J］.Communications Technology，2012，45(10):21 －23.

［8］ TRIFONOV P.Efficient Design and Decoding of Polar Codes［J］.IEEE Transaction on Communication，60(11)，2012:3221 －3227.

［9］ LIHui－ jun，YUAN Jin － hong.A Practical Construction Method For Polar Codes in AWGN Channels［C］//IEEE Tencon.Sydney，:［s.n.］，2013:223 －226.

［10］ CHUNG S，RICHARDSON T J，URBANKER L.Analysis of Sum Product Decoding of Low－density paritycheck Codes Using A Gaussian Approximation［J］.IEEE Transaction on Information Theory，47(02)，2001:657－670.