Gold序列互相关性的新证明及非最大Gold序列性质研究*

王玉东，刘春雷

(上海交通大学 数学系，上海200240)

0 引言

伪随机序列，简称PN(Pseudo－Noise)序列，在现代扩频编码理论中扮演着重要角色。常见的伪随机序列有m序列，Gold序列，M序列，以及序列偶［1］等。其中Gold序列作为m序列的延伸，以其码字数量多、互相关性好等特点得到了广泛的应用，例如我国的北斗卫星通信系统［2］。Gold序列以美国Magnavox实验室的工程师Robert Gold命名，他研究了一种特殊m序列优选对的互相关性［3］，优选对的采样因子取为d=2k+1，满足gcd(k，n)=1，其中n是对应m序列的寄存器级数，且n为奇数，并且证明了这种优选对的互相关系数为三值的，最大取值为+1。这是Gold序列得以应用的理论基础。1966年，Kasami将采样因子的条件放宽至n/gcd(k，n)为奇数［4］，并证明了这时序列的自相关系数和互相关系数也都为三值的。此后，Niho，Welch以及 Dobbertin等人研究了采样因子d取为其他值的情形［5－7］。

Kasami的证明将扩频码视为循环码，应用了循环码的理论。文中提供了一种从Gold序列和互相关系数的定义出发，利用有限域上迹函数(trace)性质的直接证明方法，并去掉了采样因子d=2k+1中k的任何限制条件。不过，当k不满足n/gcd(k，n)为奇数时，采样得到的序列不是m序列，而是非最大的移位寄存器序列，因此这种情况下我们称之为非最大Gold序列。以下是文中的详细证明。

1 基础知识

一般通信中的序列，是指具有固定周期的0、1序列，即序列 a0a1a2a3…，满足 ai∈{0，1}，以及对任意i，有ai=ai+N，其中N为序列的周期。实际应用中要求这种序列必须满足0、1平衡(即一个周期中0和1的数量几乎一样多)，以及具有良好的伪正交性等。评价序列的伪正交性常用序列的自相关函数和互相关函数。序列ai的自相关函数Pa(τ)以及相同周期的两个序列ai和bi的互相关函数Pa，b(τ)分别定义如下:。除此之外，如果其他 Pa(τ)和(τ)的取值远小于 N，我们就称序列有好的自相关性和互相关性。这与数学上一组正交族的正交性的概念十分相似，因此也称为伪正交性。

以伪随机序列中最常用的m序列为例。m序列，即最大线性移位寄存器序列，由线性反馈移位寄存器生成，具有生成方便、自相关性好等优点。常见的m序列的定义是指满足某种线性反馈条件的序列，不过在理论研究时，我们常用的是m序列的另一个定义，即用有限域上的迹函数得到的m序列的通项公式，定义如下:

由有限域的理论可知，α的特征多项式即为移位寄存器的特征多项式。利用以上定义可以很方便的计算出m序列的自相关函数满足:

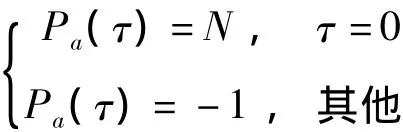
这是周期为奇数的序列所能达到的最好自相关性，称为理想的自相关性(ideal autocorrelation)。m序列具有理想的自相关性，然而不同m序列之间的互相关性十分不规律，这限制了m序列的应用。Gold、Kasami等人研究了m序列和其特定的采样序列之间的互相关性(序列ai的采样序列bi定义为bi=ad*i，其中d为正整数，称为采样因子。可以证明，m序列的互素采样序列仍为m序列)，发现这时它们的互相关函数取值为三值的，具有较好的互相关性。具体来说，他们证明了以下定理:

定理1 ai=tr(αi)为某个周期为N=2n－1的m序列，将采样因子取为d=2k+1，满足n/e为奇数，其中e=gcd(n，k)为它们的最大公因数，这时的采样序列记为bi=ad*i=tr(αdi+u)，这两个序列的互相关函数 Pa，b(τ)为:

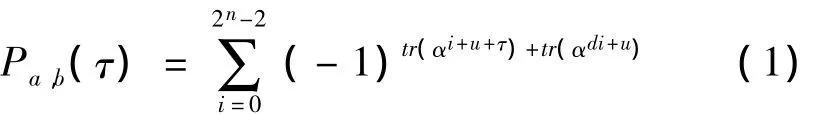
选用适合定理1条件且e=1的两个m序列称为一对优选对。现在，将Gold序列定义为m序列优选对的和序列，由于两个序列采用不同的平移相加得到的序列是不同的，即=+，其中v=0，1，…，N－1是不同的平移，因此一对优选对共可产生N个不同的Gold序列，其中只有半数－1个是0、1平衡的，这就是实际应用中选用的Gold序列。考察Gold序列的自相关性和互相关性:

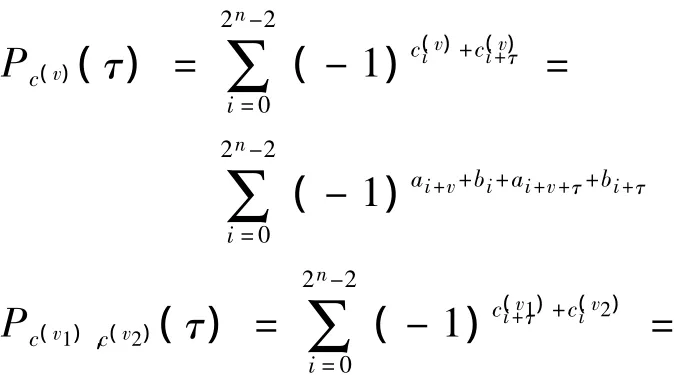
由于m序列具有性质“m序列与其平移序列的和是该序列的另一个平移”，上面两个和式在一个周期上求和后，仍然变为式(1)中的某个值，因此Gold序列的自相关函数和互相关函数都为三值的，且取值同于定理1中的取值。这是Gold序列相对于m序列的优点之一，即拥有较好的互相关性。

Kasami在证明定理1时是将序列视为循环码，用到了循环码的理论，证明过程比较繁琐。下一节中将提供一种直接从定义出发，利用有限域上迹函数性质的巧妙证法，且该证法可以很方便的推广至非极大Gold序列的情形。

2 定理1的证明

首先需要一个引理，以看清楚定理1中的条件。

引理 1 n，k为正整数，e=gcd(n，k)，则gcd(2n－1，2k+1)=1的充要条件是n/e为奇数。

证明 2k+1和2k－1是相邻的两个奇数，一定互素，因此

现在，要使 gcd(2n－1，2k+1)=1，需要上式右边分子分母相同，即 gcd(n，2k)=gcd(n，k)，这就要求k含的2因子数大于或等于n含的2因子数，也就是n/e为奇数，引理证毕。

于是，定理1中n/e为奇数的条件，保证了采样为互素采样，否则得到的bi将不是m序列，不再具有平移相加的性质，这种情况我们将得到非最大Gold序列，后面会看到，这种序列的自相关函数和互相关函数会是五值的。

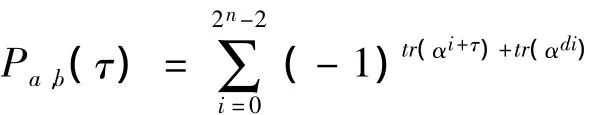
将上面的和式视为有限域上的求和，i取遍0，1，…，2n－2 时，αi取遍域 F2n中的所有非零元，再令ατ=a，因此只需求出下面的和:

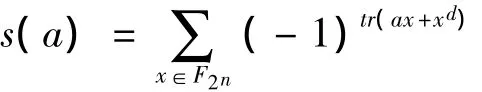
求s(a)的方法是令a取遍F2n，计算:

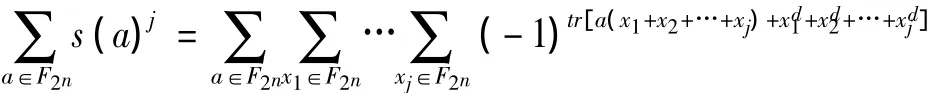
其中j是任意正整数。交换求和号，并利用有限域上迹函数求和的性质:

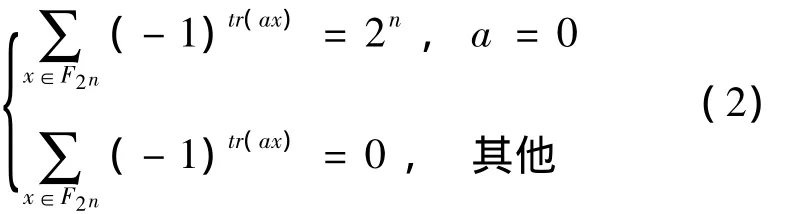
于是前式变为:

引理2 j≥3为正整数，Tj的定义如上，则:

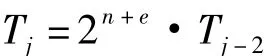
证明 注 意d=2k+1，于是在域F2n上:

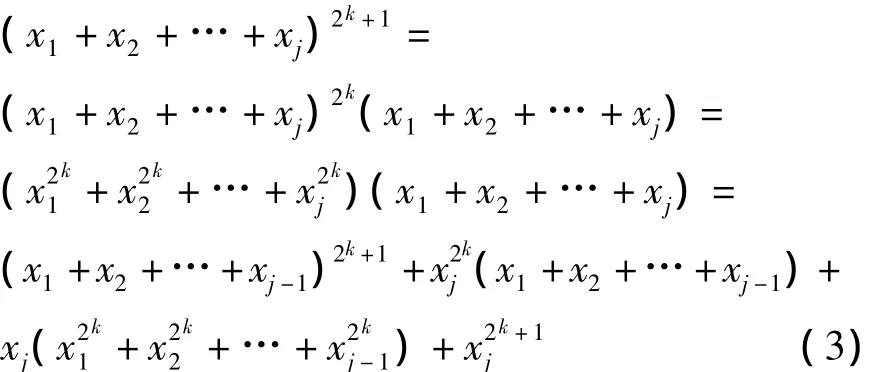
上式代入Tj的定义，利用性质tr(x)=tr(x2)以及交换求和号，Tj变为:

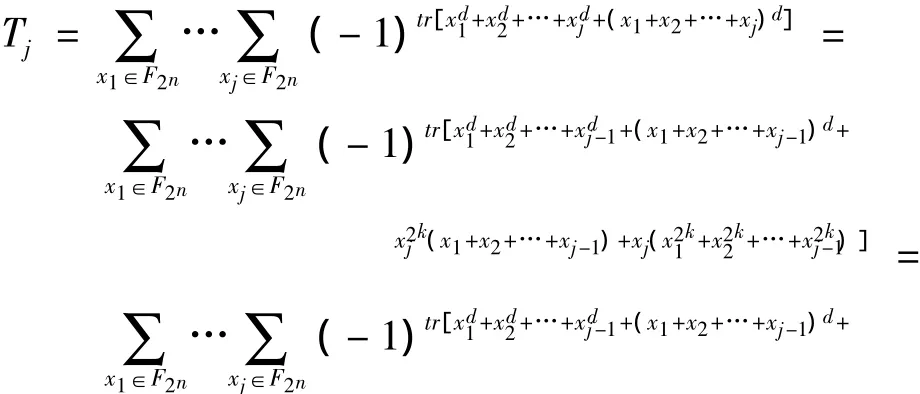
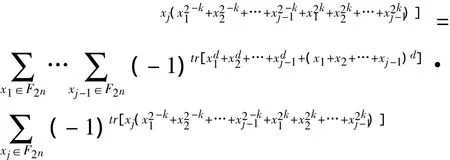
利用性质(2)，可知需要一组满足方程

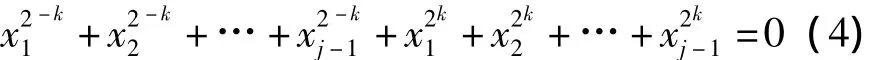
的x1到的解，只有这样后半部分求和号才不为0。将方程(4)中 x1到视为常数视为变量，这是关于的一个非齐次线性方程，且有一个显然的解=x1+… +，对应常数项为 0 的齐次线性方程为:

不考虑零解时，整理变为:

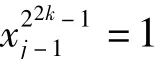
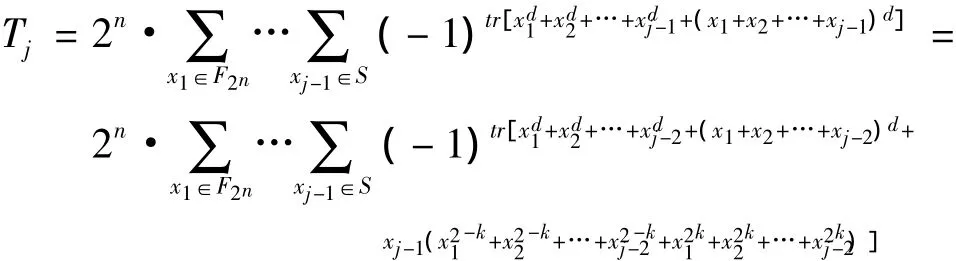
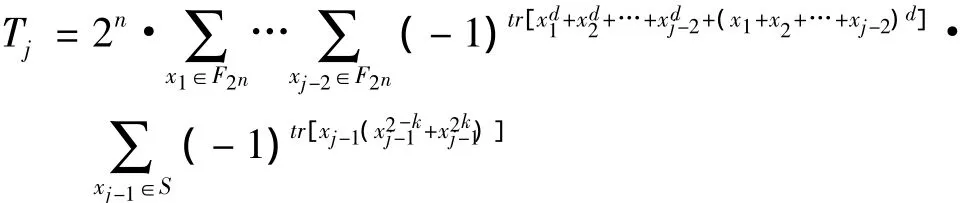
因此得

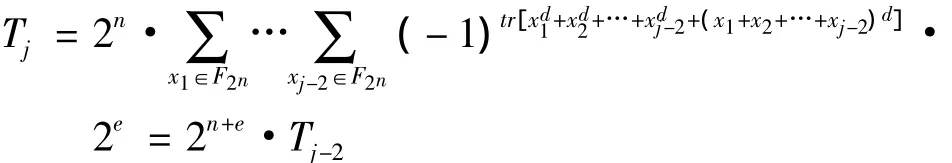
引理证毕。

可以很简单的算出T1=2n，于是j=2m－1取奇数时，=，也就是

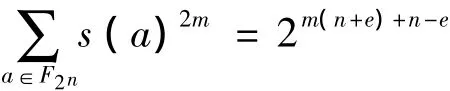
现在，对于域F2n一共2n个s(a)的值，分别设为 y1，y2，…，y2n，那么上式就是:

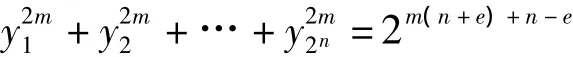
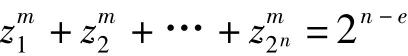
上式左端是非负zi的任意m次幂的和，右端是固定值，那么zi只可能取值0或1，且取1的次数恰为2n－e。一步步还原回去，即可知s(a)只可能取值0或±2(n+e)/2，且取 ±2(n+e)/2的共有 2n－e个，取 0 的有 2n－2n－e个。前者分别取正负的个数可由下式算出:设取正值的有t个，取负值的有2n－e－t个，则:

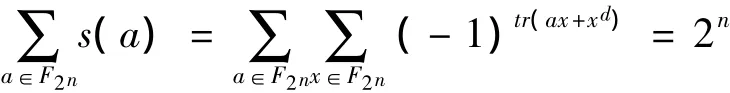
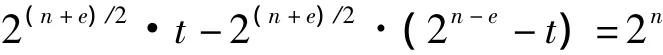
3 非最大Gold序列

本节讨论定理1没有解决的情形。引理1告诉我们，n/e不为奇数时，令 f=gcd(n，2k)，则有 f=2e，此时 gcd(2n－1，2k+1)=2e+1，不是互素采样，经采样后得到的序列bi不是m序列，但由采样的定义可知bi仍具有bi=tr(αdi+u)的形式，此时的和序列我们称为非最大Gold序列。本节将讨论非最大Gold序列的自相关性和互相关性。

沿用定理1中的记号。仍然从式(1)中 Pa，b(τ)的定义出发，这次不同的是由于d不再与N互素，我们不能像第3节开始那样将u处理掉，必须带着运算。令 a=αu+τ，b= αu，仍将 Pa，b(τ)转化为有限域上的指数和，需要求下列指数和:

与之前不同的是和式中多了一个参数b。我们有如下定理:

定理2 sb(a)定义如上。则当b是域F2n中的d阶元时，sb(a)的取值和次数分别为:当b不是域F2n中的d阶元时，sb(a)的取值和次数分别为:

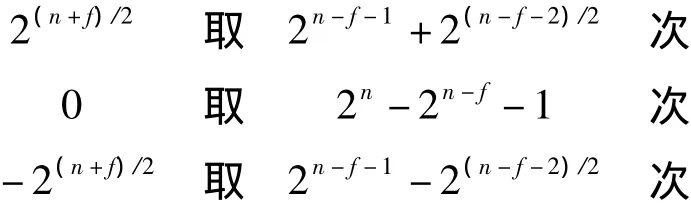
证明 使用与定理1的证明相同的方法，类似的步骤省略，重点看b的引入引起的不同之处。

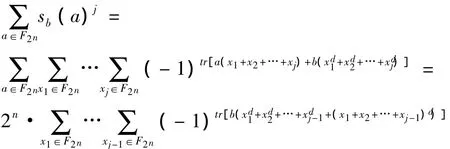
仍令

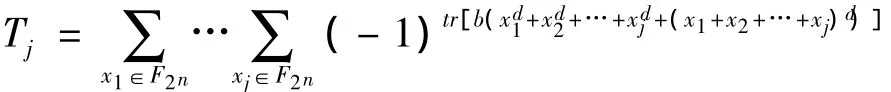
继续使用分离变量的方法:

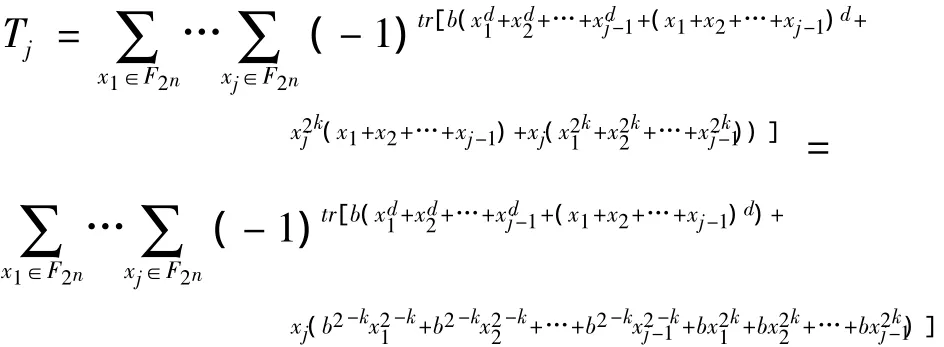
注意由于b的引入，对tr内部的幂次进行处理时，连带引起了b幂次的变化，产生了b2－k的项，这是与之前不同的地方。现在，需要处理的方程是:

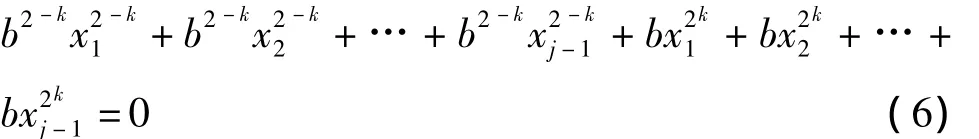
这仍是 xj－1的线性方程，xj－1=x1+ … +xj－2为一显然解，对应的齐次线性方程是

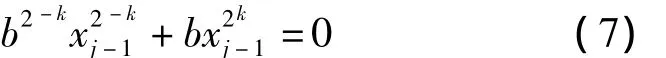
将之变形为:

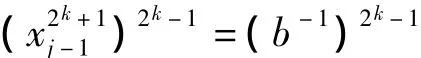
由于d=2k+1与2n－1不互素，因此分情况讨论:当b是域中的d阶元时，上述方程有gcd(2n－1，22k－1)=2f－1 个解，对应方程(7)有 2f个解，也即方程(6)有2f个解;当b不是域F2n中的d阶元时，上述方程无解，对应方程(7)只有零解，也即方程(6)只有一个解。

后续的处理跟定理1中的证明完全相同，此时引理2的结论变为:继续按相同的方法处理，于是当b是域F2n中的d阶元时，sb(a)可能的取值为0或 ±，当 b不是域F2n中的d阶元时，可能的取值为±2n/2。具体取值次数的计算方法也相同，最终结果即为定理2的结论。定理2证毕。

确定了sb(a)后，减1 即得对应Pa，b(τ)的取值，注意sb(a)的取值里多出一种a=0的情形，不过sb(0)的取值与b有关，即我们无法确定Pa，b(τ)的取值要在定理2中的哪一类里少一次，唯一可以确定的是sb(0)不会取0。因此Pa，b(τ)取值的结论要复杂一点。我们总结为如下定理:

定理3 ai=tr(αi)为某个周期为N=2n－1的m序列，采样因子取为d=2k+1，满足n/e为偶数，其中e=gcd(n，k)为它们的最大公因数，f=(n，2k)=2e。采样序列 bi==tr()，令 b=αu，则当b是域 F2n中的 d阶元时，Pa，b(τ)的取值和次数分别为:

以上第一种或第三种情形取值少取一次。b不是域F2n中的 d阶元时，Pa，b(τ)的取值和次数分别为:以上两种情形的某一种取值少取一次。

来看此时构造出的非最大Gold序列的自相关性和互相关性。令，选取得到的序列中0、1平衡的那些，自相关函数和互相关函数仍如第一节中的形式。ai是m序列，平移相加后是本序列的另一个位移;但是bi不是m序列，没有平移相加的性质因此对应到定理 3 中无法确定这个是否为域F2n中的d阶元，因此这时自相关函数和互相关函数可能取到定理3中所有的五个值，即非最大Gold序列的自相关函数和互相关函数，除了自相关函数τ=0时的一个平凡取值2n－1外，为五值的，可能的取值为－1，－1±2n/2和－1±。这五个值的取值次数没有简单的确定方法。

下面用一个非最大Gold序列的例子来阐述我们的结论。取n=6，本原多项式f(x)=1+x+x6产生的周期为63的m序列为:

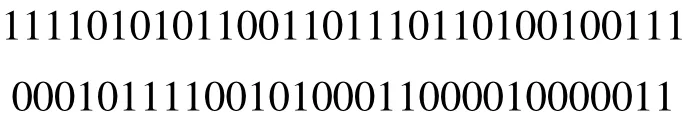
采样因子取为 d =3，于是 k =1，e=1，f=2，采样得到的序列为:

分别取平移量v=0和v=1，将上面两序列相加，得到两个0、1平衡的非最大Gold序列和分别为:

经计算，ci(0)的自相关函数取值分别为:63(取1次)，－17(取2次)，15(取2次)，－9(取18次)，7(取18次)，－1(取22次)和的互相关函数取值分别为:－17(取3次)，15(取4次)，－9(取15次)，7(取21次)，－1(取20次)，与我们得到的五值性结论相符。

4 结语

Gold序列是通信技术中有重要应用价值的一种伪随机序列。Gold、Kasami等人完成了Gold序列理论的证明。文中提供了一种更直接和巧妙的证明方法，并自然推广到了前人未提及的情形——非最大Gold序列。从上节讨论可以看出，非最大Gold序列具有和Gold序列相似的自相关性和互相关性，相关函数的取值较为平滑，具有一定的应用价值。目前，对于m序列互素采样序列的相关性研究较多，但当采样为非互素采样时，得到的非m序列及相关衍生序列等，因为性质比较复杂，目前研究较少。希望本文中用到的有限域上指数和的理论，以及证明思路等，对这个方向的研究能有所启发。

［1］ 霍晓磊，康霞.序列偶扩频通信系统性能分析［J］.通信技术，2011，44(08):1 －3.HUO Xiao － lei，KANG Xia.Analysis on Sequence －Pairs Spread Spectrum Communication System［J］.Communications Technology，2011，44(08):1 －3.

［2］ GAO Xing－xin，CHEN Alan，LO Sherman，etal.Compass－M1 Broadcast Codes in E2，E5b，and E6 Frequency Bands［J］.IEEE Journal of Selected Topics in Signal Proceeding，2009，3(04):599 －612.

［3］ GOLD R.Maximal Recursive Sequences with 3－Valued Recursive Cross－ Correlation Functions［J］.IEEE Transactions on Information Theory，1968(14):154－156.

［4］ KASAMI T.Weight Distribution Formula for Some Class of Cyclic Codes［R］.Urbana:Coordinated Science Lab.Tech.Rep.R －285，Univ.Illinois，1966.

［5］ NIHO Y.Multivalued Cross－ correlation Functions between Two Maximal Linear Recursive Sequences［D］.Los Angeles:Univ.Southern Calif.，1972.

［6］ WELCH L R.Trace Mappings in Finite Fields and Shift Register Cross－correlation Properties［R］.Los Angeles:Electrical Engineering Department Report，Univ.Southern Calif.，1969.

［7］ CUSICK TW，DOBBERTIN H.Some New Three－Valued Crosscorrelation Functions for Binarym － Sequences［J］.IEEE Transactions on Information Theory，1996，42(04):1238－1240.