双红外导引头信息融合三维角度约束制导方法

张 旭 周 军 呼卫军

西北工业大学精确制导与控制研究所，西安 710072



双红外导引头信息融合三维角度约束制导方法

张 旭 周 军 呼卫军

西北工业大学精确制导与控制研究所，西安 710072

两个拦截器的红外导引头对目标飞行器进行同步观测，而后进行集中式多传感器信息融合。信息融合目标运动估计采用交互式多模型方法IMM，使用常速度模型CV和自适应加速度模型ACA描述目标的运动，滤波器采用成熟的扩展卡尔曼滤波EKF。设计视线运动规律，拦截器按照此规律运动便可以期望的视线角命中目标。基于Lyapunov稳定性理论，得到了实现视线运动、使脱靶量和指令角度偏差收敛于0的加速度指令。最后数值仿真证明滤波系统与制导律配合工作可以完成对目标的拦截，脱靶量平均值小于0.2m，视线角度偏差小于1°。

多源信息融合；目标运动分析；角度约束制导

大气层外拦截器所使用的红外导引头仅能提供目标角度信息，限制了制导律的使用。本文通过2枚拦截器的导引头观测目标，进行目标运动信息估计，并以此为基础设计角度约束制导。

多红外导引头目标信息融合估计属于被动多传感器机动目标跟踪范畴。红外导引头不能提供距离信息，必然面对非线性跟踪问题，这一直以来是目标跟踪领域面临的挑战。多传感器信息融合，以及被动跟踪领域已有的一些学术专著及论文，多是纯数学研究，没有应用于大气层外拦截的适应性研究。

对于机动目标跟踪，需要多个模型对目标运动的不同阶段进行描述，所以滤波系统架构采用交互多模型算法[1]。常用的目标运动模型有CA模型、CV模型、非零均值时间相关模型等，非零均值时间相关模型动态跟踪性能与CA模型持平[2]，单个CA模型无法精确描述目标运动，故使用CV模型、新型的自适应加速度模型ACA来描述目标运动。滤波算法选定研究较多的扩展卡尔曼滤波EKF[3]。

在固定目标角度约束拦截[4]的基础上，推导出了基于Lyapunov稳定性理论的，针对机动目标的三维角度约束制导律。数值仿真证明滤波系统与制导律协同工作可以圆满完成对目标的拦截。

1 目标信息估计

考虑2个(拦截器)导引头对目标进行观测的情形。目标信息估计一般由目标运动建模和滤波算法2部分构成。采用IMM方法对2个目标信息估计单元进行综合。

1.1 目标运动模型

1) CV模型

当目标不进行机动时，常速度模型可以精确的描述运动状态。为了与ACA模型构成IMM，将常见的6维模型扩为9维。拦截弹1的运动参数记作rmx1,rmy1,rmz1,vmx1,vmy1,vmz1,amx1,amy1,amz1；拦截弹2的运动参数记作rmx2,rmy2,rmz2,vmx2,vmy2,vmz2,amx2,amy2,amz2；目标的运动参数为(rtxrtyrtzvtxvty

vtzatxatyatz)=x。滤波系统状态方程为

x(k+1)=Gx(k)+Γw(k)

(1)

(2)

其中，T为采样周期。观测方程为

(3)

其中，vx1(k)等为观测噪声。系统噪声特性如式(4)，式中的q1，q2和q3等作为滤波系统参数根据目标特性指定。

Q=

(4)

2)自适应加速度模型ACA

当目标机动时，常速度模型描述运动状态的准确度不够。由于目标的机动状况未知，选择ACA模型，根据目标运动的滤波结果修正系统噪声矩阵Q。这样CV，ACA两个模型就可以较完善的描述目标运动，降低了运算量。滤波系统状态方程和观测方程同式(1)和(3)，但系数矩阵和噪声特性矩阵发生变化[2]。q1，q2，q3等参数不再根据经验事先指定，而是在滤波过程中在线修正[2]。

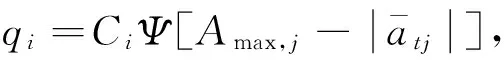
(5)

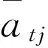
1.2 EKF滤波算法

雅克比矩阵为

(6)

其中，

(7)

1.3 扩展卡尔曼滤波交互式多模型EKF-IMM算法[1]

1) 模型交互。

2) 模型滤波。

分别对CV模型、ACA模型采用EKF滤波。

3) 模式概率更新。

4) 估计融合。

2 角度约束制导方法

2.1 制导律设计

三维情况下弹目相对运动如图1。无下标字母表示的坐标系为惯性系，下标L坐标系为视线系，下标M坐标系为拦截弹速度系(简记M系)，下标T坐标系为目标速度系(简记T系)。视线系与惯性系之间，M系、T系与视线系之间的欧拉角按照2-3转换定义。各角的正负定义如图所示，ϑL等在-90°～90°之间取值，ψL等在-180°～180°之间取值。相对运动由下式描述。

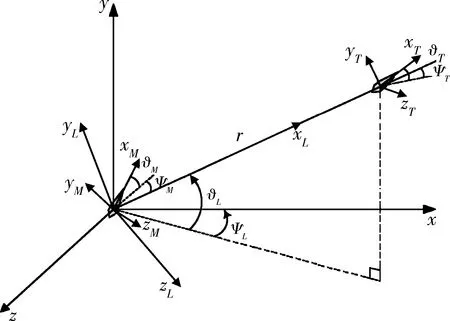
图1 目标、拦截器相对运动关系

(8)

AT=AyTjT+AzTkT=ΩL×VT+ΩT×VT

(9)

AM=AyMjM+AzMkM=ΩL×VM+ΩM×VM

(10)

(11)

(12)

(13)

为了描述拦截弹相对目标的攻击方向，精确起见应该以ψM+ψL和ϑM+ϑL作为控制目标，但为了便于理论分析和实际应用，选择ψL，ϑL作为攻击角度[4]。设期望的攻击角度为ψLC，ϑLC，设计期望的视线角运动学如下：

(14)

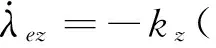
(15)

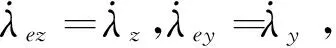
(16)

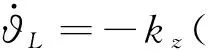
(17)

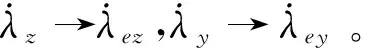
(18)

当选取

(20)

有

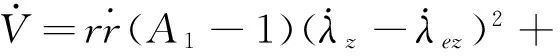
(21)

当期望的攻击角度ψLC，ϑLC为常值时，由式(14)和(15)可得

(22)

(23)

2.2 制导律分析

1) 制导律机理分析

Lyapunov稳定性理论得出的制导律形式复杂，物理意义不够明显。为了分析方便，对拦截弹攻击静止目标的情形仿真。拦截弹初始位置为惯性系原点，速度(1500,4000,-500)，目标位置(30000,80000,-10000)，拦截弹的初始速度是指向目标的。拦截弹速度系横向、法向可用过载为10g。

图2为拦截弹攻击轨迹曲线，5°偏差弹道指期望攻击视线角与视线角初值相差5°时的弹道，10°偏差弹道类似。可以发现拦截弹首先按照给定的攻击角度对准目标，之后再尽量沿直线攻击目标。加速度曲线(图 3)，说明首先过载指令使得视线趋近期望值，而后的反方向过载减小视线转动速度使得视线稳定在期望值。

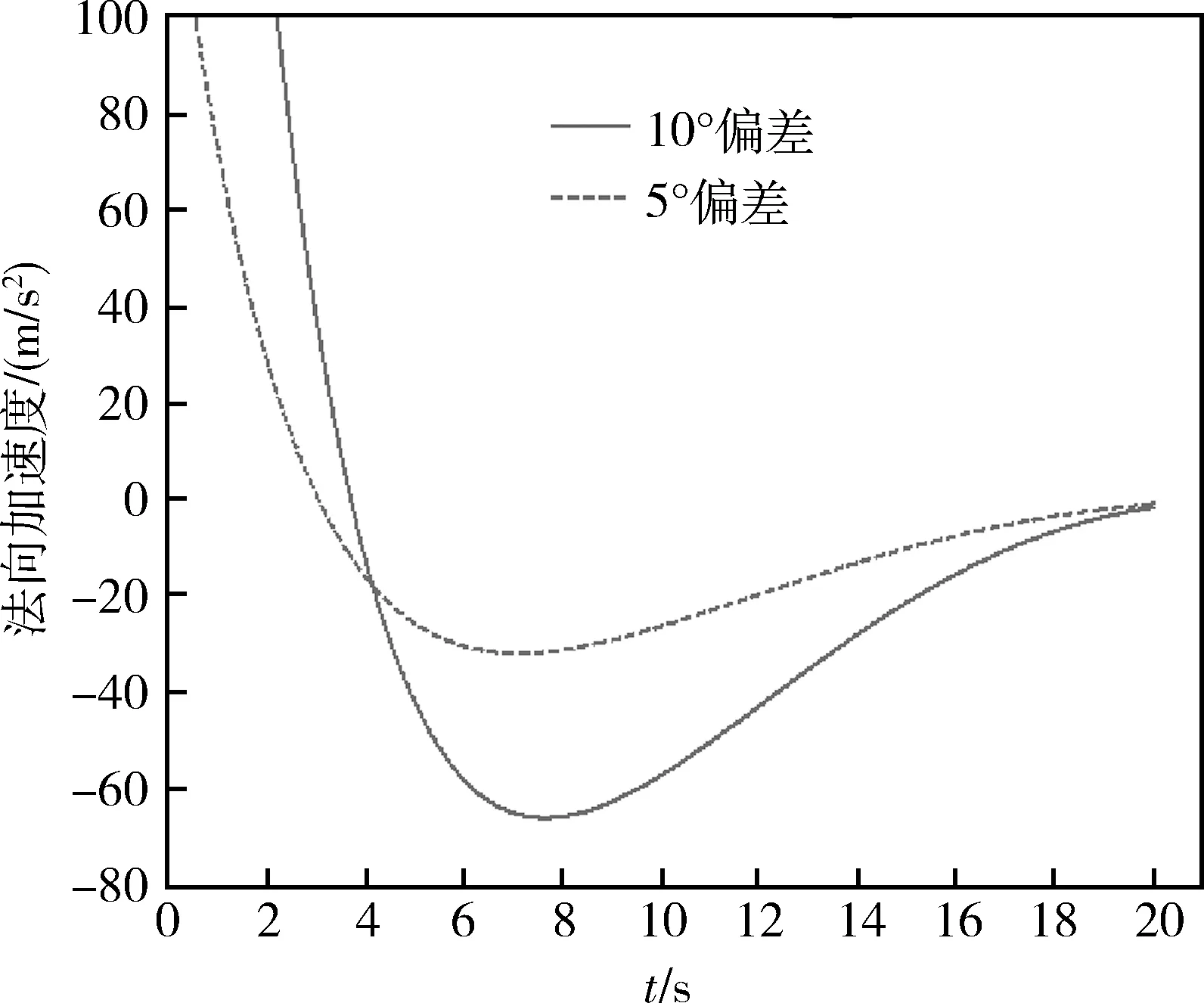
图3 法向加速度对比

2) 攻击角度范围

图3说明指令与初值偏差越大，前后方向相反的过载要求就越大。对于非静止目标，指令与初值偏差大导致拦截弹弹道弧线长度更长，花费更多时间，命中时目标距离拦截弹初始位置更近，过载需求增加就更多。受制于拦截器的可用过载，攻击角度是有限制的。对于相向运动的非静止目标，攻击角度范围更小。

3) 制导参数的选择

参数A1，A2，ky和kz提高时，由式(16-17)和(21)可知，拦截弹以给定攻击角度对准目标的速度更快，从而命中角度精度高，但也带来需用过载大的问题；攻击角度范围小，易出现较大脱靶量。参数较小，需用过载小，攻击角度范围大，易出现较大角度偏差。

3 数学仿真

仿真条件贴近大气层外拦截的实际情况。拦截弹1初始位置为惯性系原点，速度(1800,4000,-300)，目标初始位置(30000, 80000,-10000)，速度(-500,-1700,0)。拦截弹2初始状态接近拦截弹1，作S形机动飞行。拦截弹速度系横向、法向可用过载为10g。目标具有法向、横向加速度，为周期5s，占空比50%的方波，幅值为(0，40，-15)m/s2，仿真周期为1ms。

滤波器相关参数：导引头角度误差均值为0，方差为1e-6弧度。CV模型系统误差q1=5，q2=5，q3=5；ACA模型Amax,x等为40m/s2；采样周期为10ms。状态转移矩阵

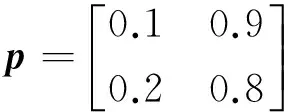
(24)

制导律相关设置：设定期望的攻击高低角为70°，方位角为28°。A1=4，A2=5，ky=kz=0.12。忽略加速度实现的动态过程。制导周期与滤波同步为10ms。

3.1 滤波器的估计精度

滤波器对z方向位置、速度、加速度的跟踪效果如图4～6所示。可以发现滤波器对位置的跟踪效果较好，对速度、加速度的跟踪快速性一般。

图4 位置跟踪结果

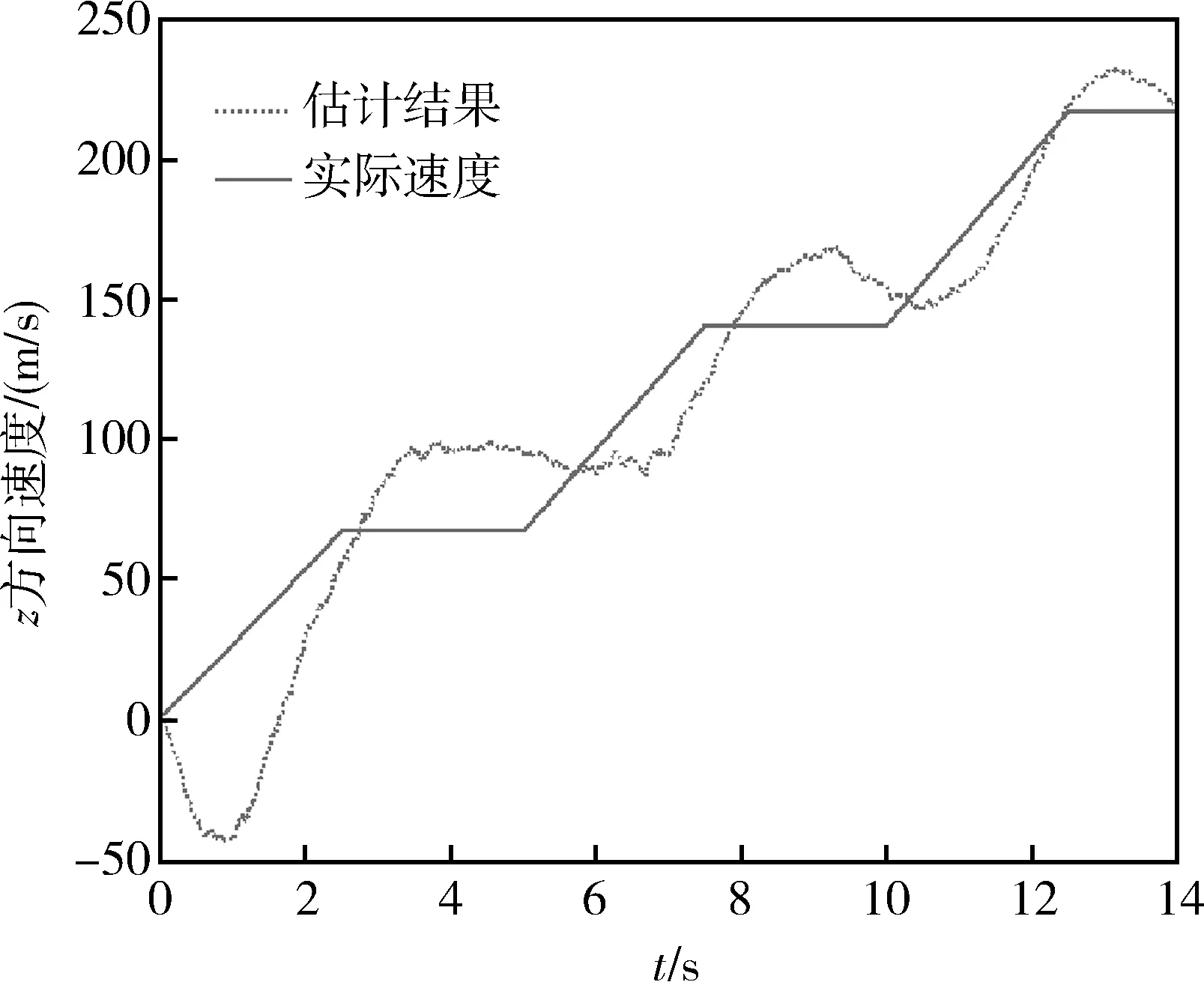
图5 速度跟踪结果

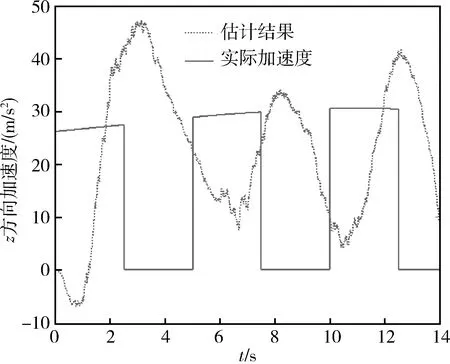
图6 加速度跟踪结果

交互多模型滤波IMM在每个滤波周期对各个滤波器的输入、输出按混合概率进行混合，所以IMM对于匀速目标的估计不如CV模型，对匀加速目标的估计不如参数设置符合真实值的CA模型，但是面对机动状况未知的目标，IMM的效果是最好的。真实的空间攻防对抗场景下，目标的躲避方式难以预测，所以IMM最具有实用价值。

3.2 滤波器制导律协同工作

考虑滤波器、制导律作为一个整体的工作效果。图 7为对机动目标的攻击弹道，图 8为制导律输出的速度系下的横向、法向加速度。图 9为指令视线角与实际视线角偏差的变化过程。

图7 机动目标攻击弹道

图8 法向、横向加速度

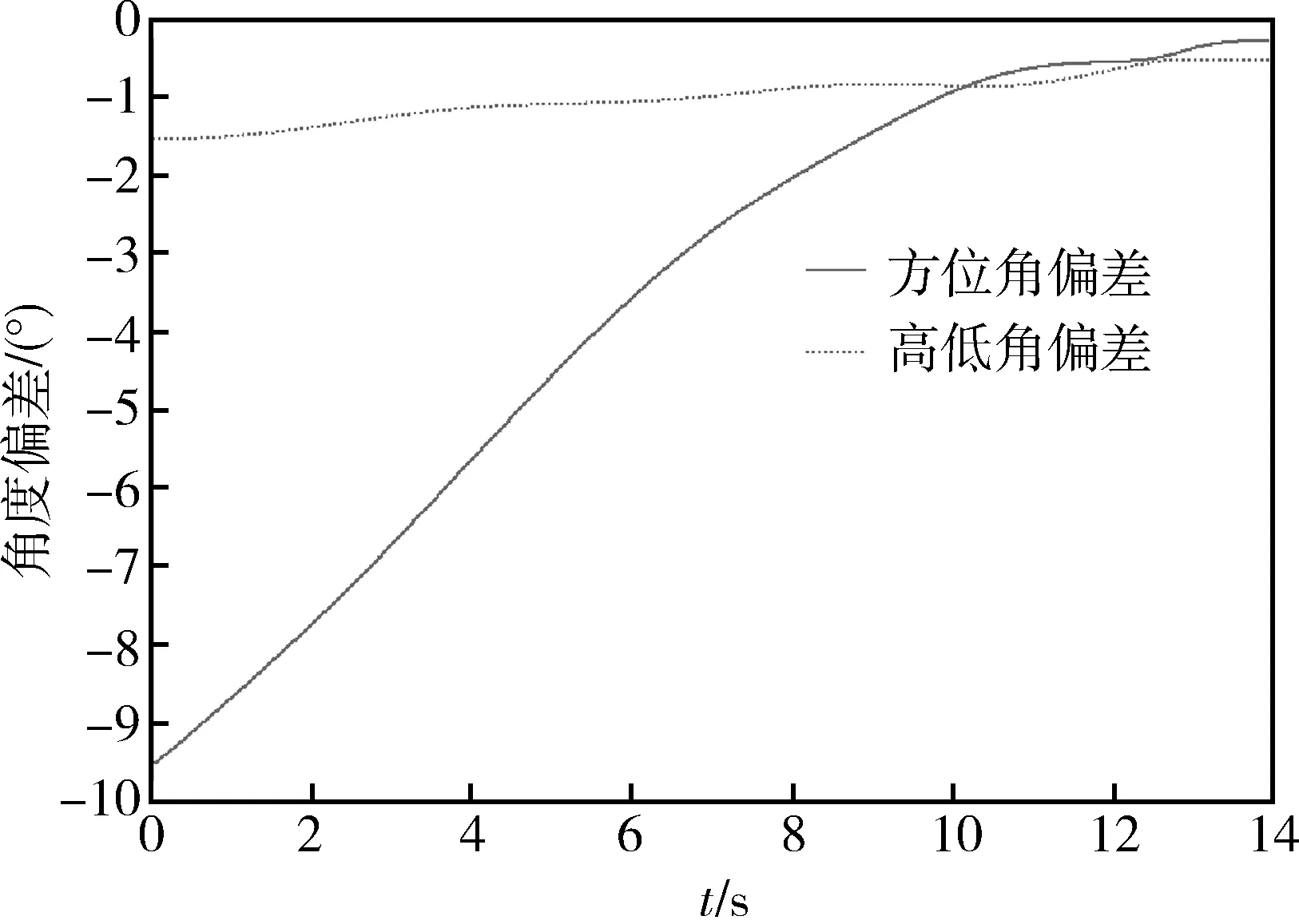
图9 视线角的收敛过程

考虑到滤波器的累计误差，为了实现零脱靶量，当估计的弹目距离小于5km时，将制导律切换为直接使用导引头输出的比例导引，这样既降低了脱靶量，也不会产生大的视线角度误差。最后结果为：脱靶量0.1m，方位角偏差0.30°，高低角偏差0.55°。虽然制导律需求的信息较多，滤波器给出的估值也存在一定误差，但这一系统整体可以圆满完成以指定角度直接碰撞摧毁目标的任务。

4 结论

针对机动目标的角度约束三维制导律目前还少见文献出现。针对此问题进行了深入研究，通过Lyapunov稳定性理论约束实际视线按照设定的视线规律运动，从而实现角度约束。而为了得到制导律需要的视线角速度、目标速度与加速度，提出了由CV模型与ACA模型构成的扩展卡尔曼滤波-交互式多模型方法。仿真说明滤波器的输出精度满足制导律的需求，制导律可以实现一定角度范围内的角度约束攻击。

[1] 夏佩伦.目标跟踪与信息融合[M].北京:国防工业出版社C2010:161-183.(Xia Peilun. Target Tracking and Information Fusion[M]. Beijing: National Defense Industry Press C2010:161-183.)

[2] 潘泉，梁彦，杨峰，程咏梅.现代目标跟踪与信息融合[M].北京:国防工业出版社,2009:15-36.(Pan Quan，Liang Yan，Yang Feng，Cheng Yongmei. Modern Target Tracking and Information Fusion[M]. Beijing: National Defense Industry Press,2009:15-36.)

[3] 周凤岐，卢晓东.最优估计理论[M].北京:高等教育出版社, 2009:147-149.(Zhou Fengqi，Lu Xiaodong.Theory of Optimal Estimation [M]. Beijing: Higher Education Press,2 009:147-149.)

[4] 张友安，马培蓓.带有攻击角度和攻击时间控制的三维制导[J].航空学报，2008， 29(4)：1020-1026.(Zhang Youan, Ma Peibei. Three-dimensional Guidance Law with Impact Angle and Impact Time Constraints [J]. Acta Aeronautica ET Astronautica Sinica，2008， 29(4)：1020-1026.)

[5] Song S H, Ha I J. A Lyapunov-like Approach to Performance Analysis of 3 Dimensional Pure PNG Laws[J]. IEEE Transactions on Aerospace and Electronic System, 1994, 30(1): 239-247.

[6] 周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002:97-103，148-156.(Zhou Di. New Guidance Laws for Homing Missile[M]. Beijing: National Defense Industry Press, 2002:97-103，148-156.)

The Three-Dimentional Angle Constraint Guidance Law Based on Dual-Detectors Information Fusion

ZHANG Xu ZHOU Jun HU Weijun

Institution of Precise Guidance and Control, NWPU, Xi’an 710072,China

Thecentralizedmultiplesensorinformationfusioniscarriedonafterthetargetmovementismeasuredsimultaneouslybytwoinfrareddetectors.Theinteractivemultiple,model(IMM)methodischosenasthemainframewhileconstantvelocity(CV)modelandadaptiveconstantacceleration(ACA)modelisappliedtodescribingthetargetmovement.ThematureextensiveKalmanfilter(EKF)isadoptedasfilteralgorithm.Thenanangleconstraintguidancelawisdeduced.Theinterceptorcanengagethetargetunderthegiveneyesightanglebyforcingeyesighttomoveasthedesignedpattern.TheneededaccelerationisobtainedbyusingLyapunovstabilitymethod.Itisconfirmedinthesimulationthattheestimationsystemandtheguidancelawcanguaranteeasuccessfulinterception.Themissislessthan0.2m,andtheangleerrorislessthan1°.

Informationfusion；Targetsmomentsanalysis；Angleconstraintguidance

2013-09-10

张 旭(1984-)，男，山东聊城人，博士研究生，主要研究方向为动能拦截器制导控制技术；周 军(1966-)，男，江苏常州人，博士生导师、教授，主要研究方向为航天器控制与仿真技术、现代控制理论及应用、导弹精确制导与控制技术；呼卫军(1979-)，男，陕西延安人，副教授，主要研究方向为导弹制导控制技术、近空间飞行器制导控制技术、先进控制理论及其应用和飞行器数字仿真技术。

V448.23

A

1006-3242(2014)03-0012-06