基于蚁群粒子群混合算法的多目标优化在供水管网优化设计中的应用

殷方康

( 中国地质大学，湖北 武汉 430074 )

科技与应用

基于蚁群粒子群混合算法的多目标优化在供水管网优化设计中的应用

殷方康

( 中国地质大学，湖北 武汉 430074 )

在城市供水系统中，管网的铺设费用占很大比重。如何最大限度降低建设成本而又保证供水的可靠性，是供水管网设计的重点和难点。基于供水管网的固有特性，结合蚁群、粒子群算法的优点，将蚁群粒子群混合算法应用到供水管网设计的多目标优化中。将蚁群中的信息素、启发因子、信息素挥发度参数映射到粒子群算法中粒子的位置坐标，通过粒子迭代寻找最优位置，并将蚁群算法通过特定信息素更新方式并限制迭代次数来进行优化，再将粒子最优位置反馈到优化后的蚁群算法中，寻找最优解。通过此算法，优化了供水管网中管径的选择，在保证供水管网可靠性的前提下，尽量缩减建设费用，为决策者提供更加经济实用的决策参考。

蚁群粒子群混合算法；多目标优化；供水管网

引言

在供水工程中，管网的建设费用占很大比重，因此供水管网的优化设计具有很大的经济价值。在供水管网路径设计中，如果提高供水能力，则投资费用相应升高，而一味地追求低费用，则不能满足城市的用水需求，而且存在着水质安全无法保证的问题[1]。所以单目标优化并不适用于供水管网优化设计。需在保证用水需求量的基础上，将管网建设费用降到最低，以期达到既保证管网服务性能，又节省成本，即供水管网多目标优化。多目标问题中，需要同时兼顾多个目标，但不一定使得每个目标达到最优[2]。这种情况下，一般会以牺牲某一目标为代价来获得全局的最优解。

1 多目标规划数学模型

供水管网优化设计中，要在满足管网工况设计要求的基础上保证经济性。在管线布局已经确定的情况下，需要考虑各节点的用水量及水压，来确定管线各干路、支路上流量以及水压。设计中需根据各管段上的设计流量和需水节点的设计自由水头来匹配相应的管径，由于不同的管径对应不同的造价成本，所以对于管段造价成本可以表示成关于管径的函数。

供水管网优化设计的目标是在满足供水管网可靠性即约束条件的基础上，使管网造价成本费用即目标函数最小。它的数学模型如下：

1. 1目标函数为：

(1)

Z为管网造价成本；xj为管径变量，f(xj)为j管径值所对应的造价成本；di为第i条管段的长度值；n为管段的数量，m为管径的种类数量。

1.2约束条件为：

①流量及水压约束条件：

qi≥qmin

(2)

Hmin≤Hi≤Hmax

(3)

qi为i管段的流量，qmin为管段最低要求流量；Hi为管段节点自由水头，Hmin、Hmax为节点最低、最高要求自由水头。

②水力平衡约束条件[3]：

管段流量以及需水节点自由水头需满足连续性方程和能量方程：

∑(HFi-HTi)=0

(4)

∑(±qi)+Qi=0

(5)

HFi、HTi为i管段两端节点的自由水头；Qi为i节点可利用流量。

③管径约束条件：

管径是一组离散的变量，故其取值取决于市场现有的标准管径：

xi∈{X0,X1…Xm}

(6)

1.3约束条件的罚函数处理[4]：

为将供水管网优化设计中有约束最优化求解转化为无约束求解，引入罚函数法，其适应度函数为：

f惩罚=Z+PΔH

(7)

ΔH=max(Hi-Hmin)

(8)

P为惩罚因子，其定义如下：

P=(Zmax-Zmin)/Hmin

(9)

Zmax、Zmin为惩罚前管线造价成本的最大、最小值。

2.蚁群算法在供水管网中的应用

在多目标优化上，大都通过算法来求解。多目标优化算法有加权法、约束法、线性规划法等传统优化算法，也有遗传、粒子群、蚁群群等智能优化算法。而由于蚁群算法具有能快速寻找全局最优解的特点，被广泛应用到组合优化问题中。蚁群算法最初由Marco Dorigo在1992年提出，源于蚂蚁的觅食行为研究，即蚂蚁可以在蚁巢与食物之间通过信息素的分泌来寻找最短路径[5]。

在供水管网设计中应用蚁群算法如下：在初始时，将m只蚂蚁放置在水源处，然后每只蚂蚁按照管段编号依次选择各管段的管径大小。对管径大小设置初始信息素τ，蚂蚁遍历到第i条管段时，会参考信息素来选择管径的大小。即第k只蚂蚁在遍历过程中，在t时刻经过第i条管段时，选择管径值为j的概率大小为：

(10)

当每只蚂蚁遍历所有管段之后，获得一组可行解，即每条管段上的管径值。在遍历的过程中，在每条管段上释放信息素。在遍历完成后，需要对每条管段上的信息素进行更新，包括新释放的信息素增加量以及挥发掉的信息素缩减量。

τij(t+1)=(1-ρ)τij+Δτij(t)

(11)

(12)

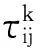
依此进入循环迭代，每次迭代都会根据本次遍历得到的最优解和全局最优解来更新信息素。当迭代次数达到指定次数或是适应值达到某一值时，终止迭代，获得最优解。

蚁群算法在供水管网优化设计中，由于其算法参数的选择决定求解的质量，而参数的选择依赖于决策者的经验和主观判断，所以蚁群算法在管径匹配上的求解性能受到一定的限制。

3.应用粒子群算法优化蚁群算法参数

粒子群算法是由Eberhart博士和Kennedy博士于1995年提出，源于对鸟群在寻找食物时的群体行为的研究[6]。粒子群算法通过随机初始化粒子位置，利用个体以及全局信息，不断迭代来更新粒子位置，寻找最优解。其特点是易实现、精度高、收敛快，并且在实际应用中展现了其优越性。

将蚁群算法中信息素相对重要程度α、启发因子相对重要程度β、信息素挥发度ρ映射到粒子群算法中[7]，即粒子的位置坐标由该三个参数来表示：

pi={α,β,ρ}

并随机产生粒子的初始速度，粒子每一维对应一个速度方向：

vi={vα,vβ,vρ}

对粒子位置初始化后，即调用蚁群算法，在迭代循环完成后，通过得到的最优解来对粒子位置的优劣进行判断，从而更新粒子速度和位置：

(13)

(14)

在粒子进行一个移步之后，需要粒子位置坐标反馈到蚁群算法中，即再次调用蚁群算法，将粒子当前位置坐标各维分量，分别赋值给蚁群算法中的信息素相对重要程度α、启发因子相对重要程度β、信息素挥发度ρ。当粒子连续迭代若干次仍未出现更优解，则终止迭代，返回一个全局最优解，即最优粒子的位置坐标，赋值到蚁群算法的参数中，即完成整个优化算法。

4 蚁群算法的优化

在粒子每个移步之后都要调用一次完整的蚁群算法，由于蚁群算法迭代次数可以高达数百次，而且每次迭代都需要更新信息素，所以上述求解算法虽能保证了求解的准确性，但大大增加了计算时间成本。故本文对蚁群算法进行了部分优化：

在调用蚁群算法时，并不是在每次迭代之后进行更新，而是当出现更优解时，才进行更新。调用一次蚁群算法之后，信息素并不清空，当下次蚁群算法开始调用时，信息素为上一次蚁群算法结束时的值[8]。由于每次调用蚁群算法时，不需要再从初始的随机解一步一步迭代，在每次开始调用蚁群算法时，已经具备了所积累的环境信息。所以可以将蚁群算法中的迭代次数设置为较小的数值，这大大节省了程序运行的时间成本。

5 供水管网优化设计流程及实例

在供水管网优化设计程序算法中，首先初始化粒子群算法中粒子位置坐标，位置坐标的每个维度分别为蚁群算法中信息素、启发因子相对重要程度以及信息素挥发度初始参数。经过粒子群一次迭代，寻找全局最优位置，将其位置坐标反馈到蚁群算法，通过调用完整的蚁群算法，寻找最优管径匹配组合，更新蚁群算法中的信息素以及全局最优解。再次对粒子群进行一次迭代，将位置坐标反馈到蚁群算法，再次调用完整的蚁群算法后，更新最优解。以此类推，直到粒子群算法中，连续迭代若干次，相应的蚁群算法中没有更优解，算法完成。流程图如图1所示：

图1 算法流程图

选取环状管网为示例管网模型，包含一个水源和9个需水节点，各节点编号、流量以及管段编号如图2所示：

图2 管网示意图

管段水头损失按照海曾威廉公式计算：

h=10.67q1.852l/C1.852D4.87

q、l分别为流量和长度；D为管径；C为海曾威廉粗糙系数，此处取130，对于最大节点流量闭合差取0.001。

粒子群数量取30，w取0.5,c1=2,c2=2,蚁群数量取30，迭代次数取3次。粒子群迭代30次，程序终止。根据市场标准管径造价，按由小到大的顺序给不同的管径进行编号。优化效果如表1所示：

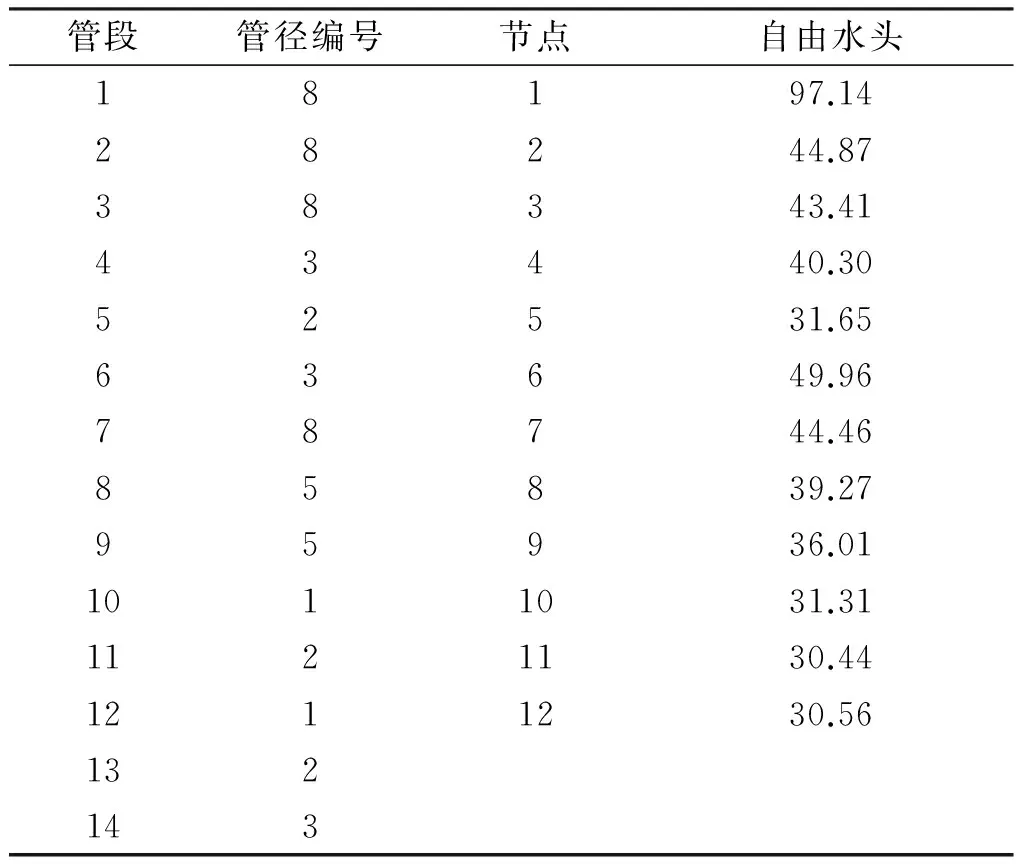
表1 供水管网优化表

6 结语

供水管网优化设计一直是城市管线系统研究的重点。针对供水管网管径选择问题，本文应用蚁群粒子群混合算法，将蚁群算法的三个重要参数赋值给粒子群算法中的例子位置坐标，通过粒子位置的寻优，反馈到蚁群算法，寻找最优解，即最优管径组合，避免了蚁群算法中参数选取的盲目性。并通过蚁群算法的优化，节省了时间成本。根据需水节点的需水量，调整相应管段的管径，保证其经济合理，故在供水管网优化设计中具有广阔前景。

[1]蔺晓. 供水管网的智能优化改扩建[D].青岛理工大学,2011.

[2]杨颖蓉,侯学良. 浅谈多目标优化决策方法[J]. 现代经济信息,2013,(15):80.

[3]乐永生. 基于MATALB的给水管网优化设计研究[D].合肥工业大学,2009.

[4]孙明月,许文斌,邹彬,何英. 基于整数编码粒子群算法的树状供水管网优化[J]. 水资源与水工程学报,2012,(06):168-171.

[5]喻江平. 基于蚁群优化的多目标资源配置模型及应用[J]. 统计与决策,2013,(14):82-85.

[6]杨亚红,王瑛,曹辉. 基于粒子群优化算法的环状管网优化设计[J]. 兰州理工大学学报,2007,(01):136-138.

[7]柴宝杰,刘大为. 基于粒子群优化的蚁群算法在TSP中的应用[J]. 计算机仿真,2009,(08):89-91.136.

[8]李擎,张超,陈鹏,尹怡欣. 一种基于粒子群参数优化的改进蚁群算法[J]. 控制与决策,2013,(06):873-878.883.

(责任编辑：孙强)

The Application of Multi-Objective Optimization of Ant Colony Algorithm and Particle Swarm Algorithm in the Design of Optimization of Water Distribution System

YIN Fang-kang

( China University of Geosciences, Wuhan, Hubei, 430074, China )

In water supply system in cities,the laying of pipe network accounts for a large proportion of the cost. It is an important and difficult part in the design of water distribution system to lower the cost and ensure the reliability of water supply at the same time. Based on the advantages of ant colony algorithm and particle swarm algorithm, this thesis applies them into the design of optimization of water distribution system with the aim to seek for the best solution. In this way, it optimizes the options of the diameter of water pipe. In the preposition of ensuring the reliability of water supply system, it can reduce the cost of construction.

colony algorithm and particle swarm algorithm; multi-objective optimization; water supply system

2014-06-20

殷方康(1989-)，男，山东莒南人，计算机学院硕士在读。

TU991

A

1671-4385(2014)04-0102-04