凹凸板换热器强化传热的数值模拟

王定标，夏春杰，董永申

（郑州大学化工与能源学院，河南 郑州450001）

板式换热器具有易拆洗、传热系数高的特点在多种工程领域得到了广泛应用，是一种高效、节能的换热器，但长久以来板式换热在增加传热量的同时，流动阻力增加的也比较大。人们曾采用多种方法来改善其流动阻力性能如粗糙或拓展传热表面来增强流道的流动传热能力，工程中常见的有肋片、波浪槽、针翅、凸胞结构等。板片表面凹坑凸胞强化传热技术与其他强化传热结构相比，在增加传热量的同时，流动阻力增加的并不高，因而近年来引起了国内外众多研究者的兴趣。国内学者对蜂窝板换热器浓缩蒸发和外部降膜传热特性进行了研究［1－2］；国外学者也有很多研究成果。Burgess等［3］取空气作为介质进行实验，研究了凹坑深度与凹坑投影直径之比对传热增强因子和阻力增大因子的影响。Hwang等［4］对上下壁面排布凹坑、凸胞、凹坑凸胞的3种结构进行实验研究，结果表明凹坑板的综合传热性能最好。Samad等［5］参考Hwang等［2］的实验结果，采用多目标优化法，对凹坑结构的凹坑间距与凹坑投影直径之比进行了优化。尽管国内外学者已做了大量研究［6－16］，但对于本文的新型凹凸板（胶囊型）研究甚少，对于不同倾角α和高度H的全面分析以及综合性能的研究还较为薄弱，本文作者针对这方面的研究薄弱环节，对多个不同α和H情况下的强化传热情况进行了综合系统的分析，并考察了各个工况下的综合传热性能。同时针对前人研究较多的球形的凹坑凸胞（酒窝板），运用场协同理论进行了两者的对比验证。

1 模型与求解

1.1 物理模型

本文研究的凹凸板实际结构如图1，由于凹凸板传热元件流道几何结构以及流动和传热的周期性及对称性，对其进行简化，确定物理模型如图2所示，凹凸结构为胶囊型。流道和几何参数如图3所示，上下板呈完全对称分布。流道高度为H′，凸胞高度为H，倾斜角度为α，本文取H′＝22mm，计算单元的长宽为160mm。本文对H＝4mm、6mm、8mm、10mm；α＝15°、30°、45°、60°的模型在Re＝3000、5000、10000、20000时进行模拟分析。

图1 凹凸板实际结构

图2 凹凸板物理模型及边界条件计算单位

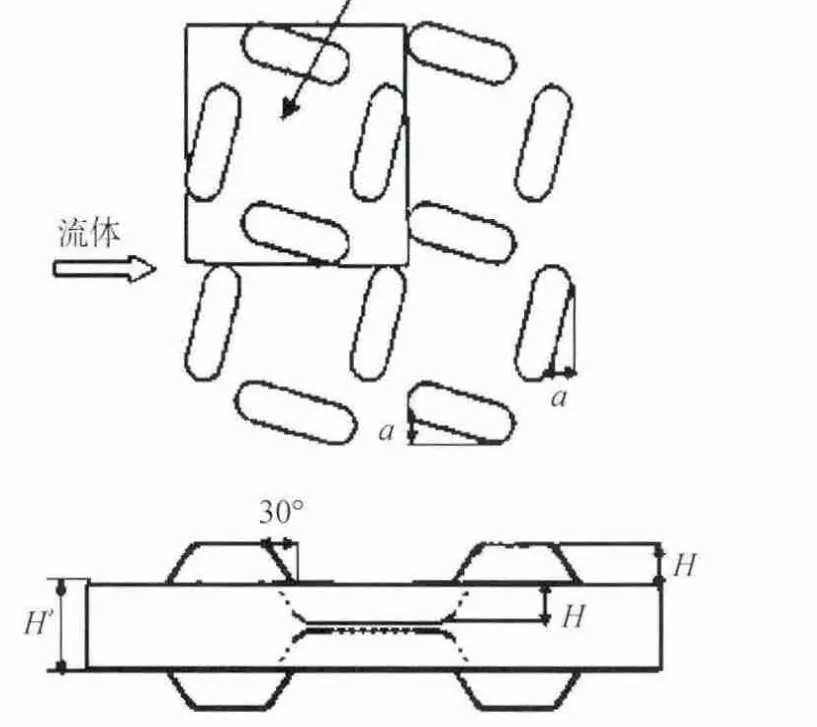
图3 凹凸板传热元件流道及几何参数

1.2 数学模型及评价指标

流体的连续方程、动量方程、能量方程可表达为如式（1）的通用形式［17］。

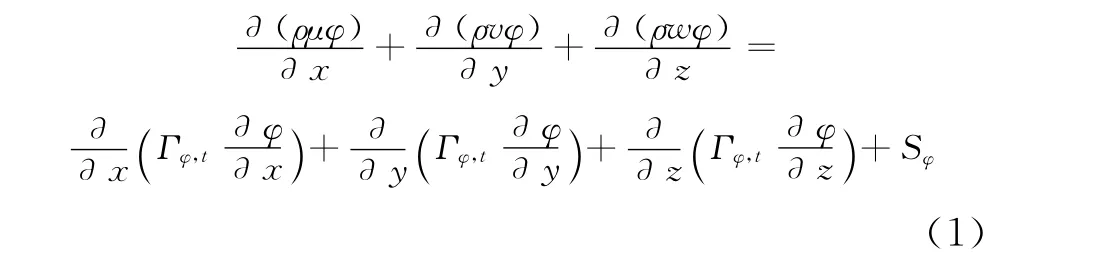
式中，ρ为流体密度；φ为通用变量；u、v、w分别表示流体沿x、y、z方向的流速；Γ为广义扩散系数；Sφ为广义源项。式（1）中第一项和最后一项分别为流体的瞬态项和源项（可以包括其他模型源项或者用户自定义源项），等号左右三项分别是对流项及扩散项。

将凹凸板传热元件传热性能、阻力性能和综合传热性能分别整理为传热增强因Nu／Nu0，阻力增大因子f／f0所以及综合传热性能增强因子η。

为保证参照基准的准确性，光滑通道的努塞尔数Nu0和摩擦系数f0和各凹凸结构一样均由数值方法得出。凹凸结构的Re、Nu、f、η分别定义为式（2）［18］。

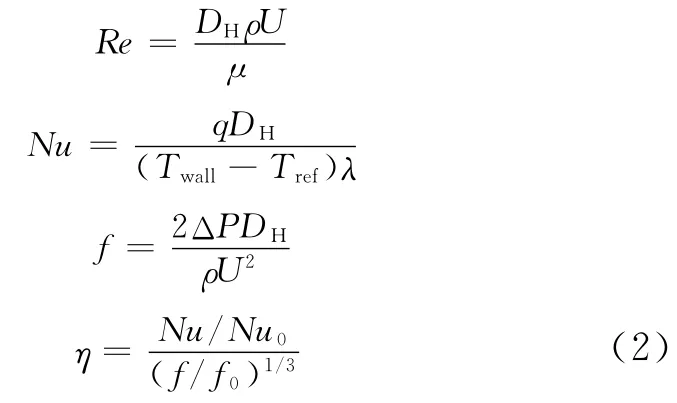
式中，μ为流体的动力黏度；q为流体热流密度；DH为通道当量直径；Twall为壁面温度；Tref为参考温度，取壁面对应区域的流体混合平均温度；λ为流体热导率；ΔP为单位长度上的压降；ρ为流体密度；U为流道截面上的平均速度。

1.3 边界条件及求解设置

边界条件如图2，具体为：①进出口面为有压降的周期性边界条件，根据不同的Re折算成质量流量Qm，并设定质量流量为初始值；②两侧面为对称边界条件；③参考前人文献，在布有凹凸的上下壁面采用恒热流边界条件对空气加热，恒热流设定为q＝800W／m2。

在计算预处理中采用Simplec算法，解算器采用三维单精度解算器，解的格式采用RNGk－ε模型进行计算。定义工质为温度30℃的空气，并且物性参数保持不变。在Fluent软件中自动使用二阶精度，各残差项的收敛精度取为10－7，其他参数取默认值进行计算。

计算区域的网格划分采用非结构化四面体网格，经网格独立性考核当网格步长取到2.3mm时，努塞尔数Nu开始基本不再发生变化，说明此时网格密度已经足够满足模拟精度的要求。

2 数值模拟方法验证及结果分析

2.1 数值模拟方法验证

为了对比验证，本文作者模拟了一组与文献［19］中相同的工况，流速为0.1～0.6m／s，做出了凹凸板在不同流速下努赛尔数的曲线图。实验值和模拟值的数据对比如图4。

从图4凹凸板Nu模拟值与实验值结果对比可以看出，两者的Nu基本一致。数值计算得到Nu与实验分析的结果相比误差都在15%的允许范围内，从而证明了用数值模拟方法获得的结果是可靠的。

2.2 数值模拟结果分析

根据模拟的结果显示，虽然流体以不同的质量流量进入流道，但流体在流道内的变化趋势是相似的。所以本节仅列出各个模型初始质量流量为0.0152kg／s、H＝10mm时 在Z＝11mm、Y＝80mm截面上的温度场、压力场、速度场的分布图作为参考。

图5显示了该截面的温度分布图，由图可知：①沿流体流动方向，出口温度比进口温度都有所升高；②凹坑周围的温度明显升高，离凹坑越近温度越高，越远温度越低；③在凹坑凸胞迎风侧，温度场分布稀疏，温度变化不大，换热趋于平缓；在背风侧，温度场分布稠密，温度递增显著，换热较强烈；④随着倾斜角度的增加温度递增较快，换热较好。

图6显示了该截面的压力分布图，由图可知：①在凹坑凸胞迎风侧出现高压区，压力明显增加；②在凹坑相接触处即流道最窄处两侧，压力先下降后回升；③倾斜角度对流道内部压力场的分布影响比较大，随着角度的增加压力梯度越来越大。

图7显示了该截面的速度分布图，由图可知：①在凹坑处流体流速发生明显变化，其他地方流速较均匀；②在凹坑附近速度方向发生变化，背风侧比迎风侧速度有所降低；③随着倾斜角度的增大，速度梯度变化越来越大。

3 数据处理与分析

3.1 雷诺数Re对凹凸板传热元件性能的影响

对不同几何尺寸的凹凸板在Re为3000、5000、10000和20000时进行数值模拟计算，并对结果进行数据处理，结果如图8。

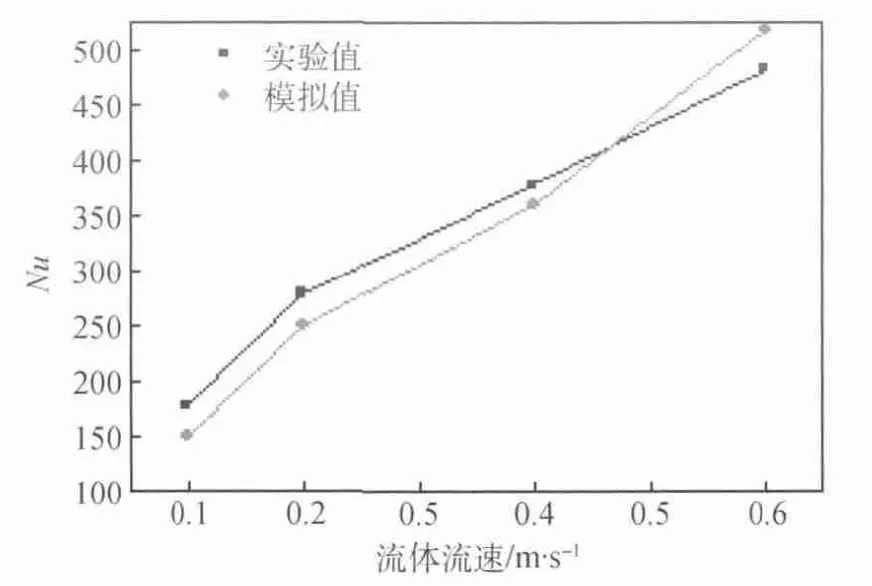
图4 凹凸板Nu模拟值与实验值对比

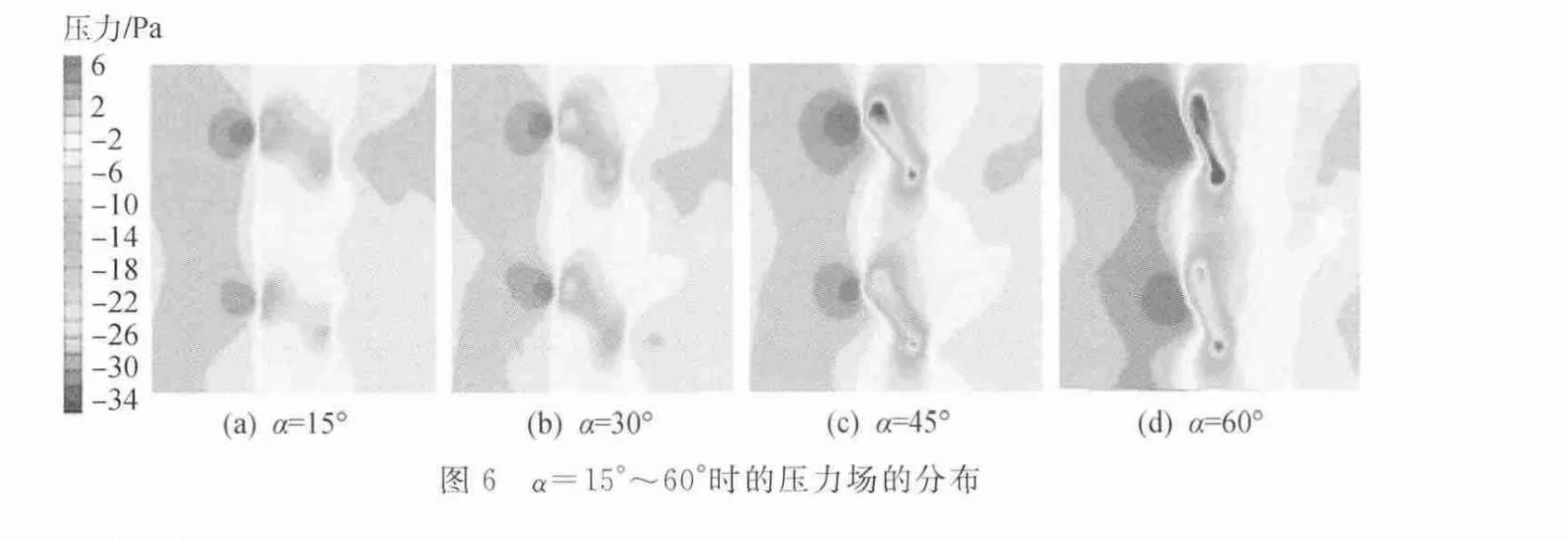
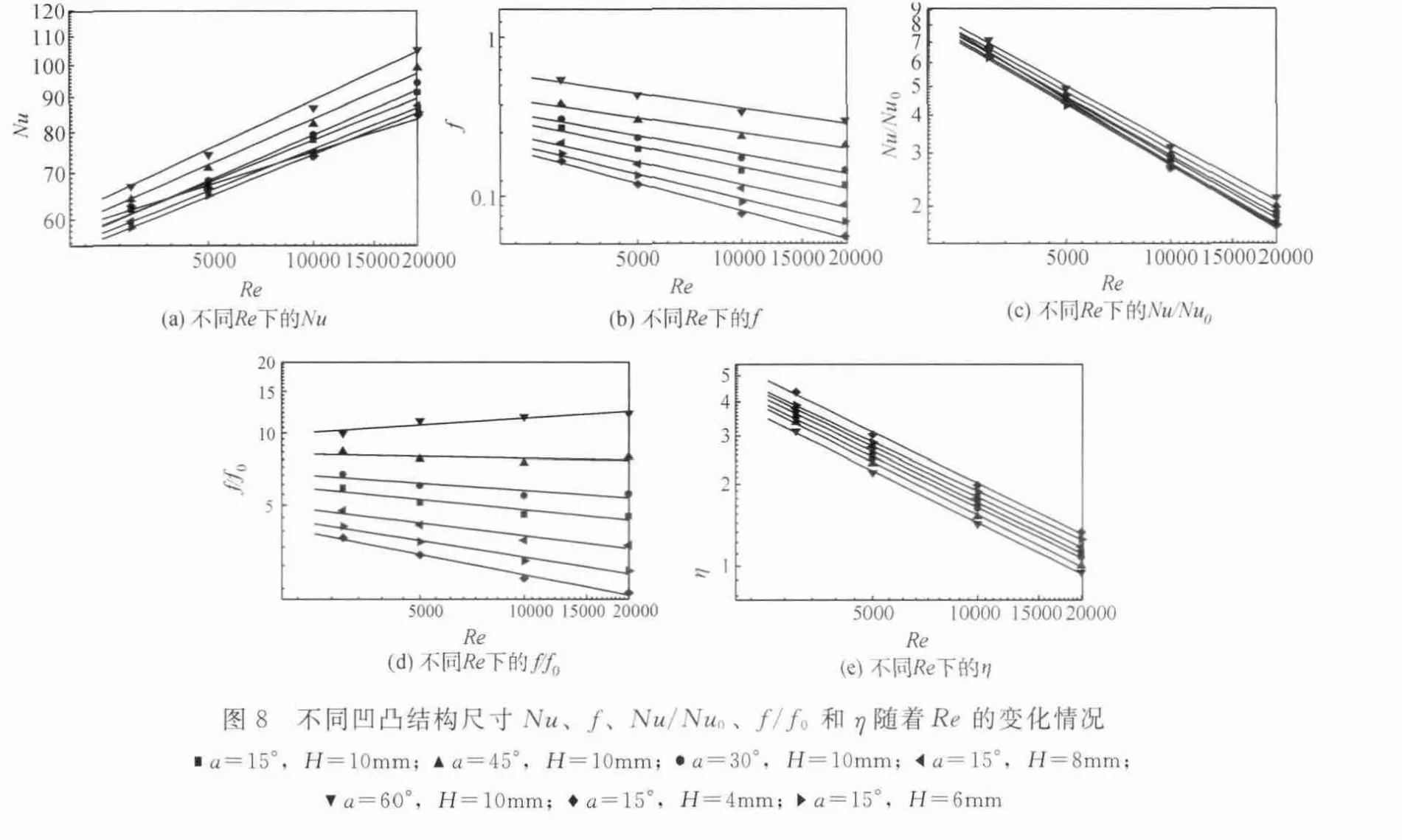
由图8可知，在3000≤Re≤20000的情况下可得出以下结论。

（1）各几何尺寸凹凸板的Nu数均随着Re的增大而成指数倍增大；而摩擦系数f、传热增强因子Nu／Nu0和综合传热性能增强因子η则均随着Re的增大指数倍减小；在不同的几何尺寸下，阻力增大因子f／f0随着Re的变化表现出不同的规律，增大、减小以及变化不大的均有。这与强制湍流对流传热系数和摩擦系数的准则关系式规律相类似。

（2）各几何尺寸凹凸板的Nu／Nu0均大于1.7，最大达到7.1，这说明凹凸板的传热效果明显比平行板的好，凹凸结构确实有明显的强化传热作用。各几何尺寸凹凸板的f／f0均大于2.0，最大达到12.1，这说明凹凸板的摩擦系数比平行板大的较多。

（3）绝大部分几何尺寸的凹凸板η均大于1，最大达到4.3，这说明绝大部分几何尺寸的凹凸板的综合传热性能较好，η随着Re的增大指数倍减小，说明凹凸板在低雷诺数下有较好的传热性能，在高Re数下凹凸板的传热优势己经不是很大。

3.2 倾斜角度α对凹凸板传热元件性能的影响

图9 不同倾斜角凹凸板Nu、f、Nu／Nu0、f／f0和η随着α的变化情况

对倾斜角度α分别为15°、30°、45°、60°共4种不同几何尺寸的凹凸板在Re为3000、5000、10000和20000时进行数值模拟计算，进行数据处理，结果如图9。

由图9可知，不同倾角的凹凸板的Nu、f、Nu／Nu0、f／f0均随α的增大而增大；且f／f0的增大幅度明显高于Nu／Nu0。所以综合传热性能增强因子η则均随着α的增大而减小。这说明α较小时，凹凸板传热性能较好。α的增大增加了绕流效果，传热效果增加但阻力系数同时也在增大，当α＝15°时综合传热效果达到最佳。

3.3 凸胞高H对凹凸板传热元件性能的影响

对凸胞高H分别为4mm、6mm、8mm和10mm共4种不同几何尺寸的凹凸板在Re为3000、5000、10000和20000时进行数值模拟计算，进行数据处理，结果如图10。

由图10可知：在不同的Re下，随着H的增大，凹凸板的Nu、f、Nu／Nu0、f／f0均逐渐增大，η逐渐减小，这主要是因为f／f0的增大幅度要明显高于Nu／Nu0。说明在H较小时，凹凸板的综合传热性能较好；而在Re＝20000，H≥6mm，η明显小于1，故此时凹凸板高度已不适合用于凹凸板的强化传热。故当H＝4mm时综合传热效果达到最佳。

图10 不同凸胞高H的凹凸板Nu、f、Nu／Nu0、f／f0和η随着H的变化情况

4 场协同分析

图11为新型凹凸板协同角分布图，根据场协同理论［20］，协同角θ体现了对流强化传热的能力，角度越小，协同性越好，强化传热能力越强。协同角的大小取决于速度矢量u和热流矢量∇¯T的夹角。θ的大小在Fluent中可以通过自定义协同角θ的场函数获得式（3）。

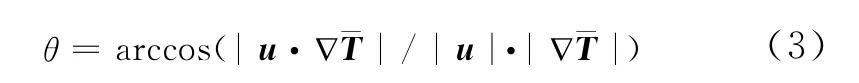
图12为本文作者研究的新型凹凸板（胶囊型α＝15°、H＝4mm）和前人较多研究的球形凹坑凸胞结构（酒窝板）协同角［21］的对比。

图11 新型凹凸板协同角分布图

图12 新型凹凸板（胶囊型）和酒窝板片协同角对比

在平板流道中，速度矢量与温度梯度的夹角几乎垂直接近90°，所以其协同程度较差，强化传热的能力也较差。在酒窝板通道中，各结构的协同角均比90°小3°多，最小的为82.70°［21］，而在此新型凹凸板换热器中，由图5和图7可以看出，在中心区域，温度梯度和速度矢量的夹角较大，在凹坑周围，产生了大量的涡旋，流体流动的方向得到改变，协同角局部减小，局部传热系数增大。经计算整个流场的平均协同角为81.91°～84.64°，比酒窝板协同角小0.80°～1.65°，速度场与温度场的协同程度有较大改善，强化换热性能也得到显著增强。

5 结 论

（1）当3000≤Re≤20000时，随着Re的增大，凹凸板的Nu成指数倍增大，f、Nu／Nu0和η随则成指数倍减小；f／f0表现出不同的规律。其Nu／Nu0的 值 为1.7～7.1，f／f0的 值 为2.0～12.1，绝大部分的η值大于1，最高达到4.3，分析表明在低雷诺数下凹凸板的传热性能较好。

（2）在15°≤α≤60°、4mm≤H≤10mm的范围内，随着α的增大，Nu、f、Nu／Nu0、f／f0均随α的增大而增大，η整体呈下降趋势；随着H的增大，Nu、f、Nu／Nu0、f／f0均逐渐增大，η逐渐减小。故当α＝15°、H＝4mm时综合传热性能最好。

（3）从场协同理论的角度分析了凹凸板换热器强化换热的机理，由于流场中的漩涡使温度场和速度场的协同性得到可改善，凹凸板内部流场的协同角为81.91°～84.64°，相比酒窝板有较大改善，换热性能得到很大改善。但胶囊板片其他参数的改变对传热性能的影响和与酒窝板更全面的对比还有待进一步研究。

［1］ 刘振义，徐尧润，宋继田.异形板外流降膜蒸发器及其研究［J］.食品与机械，1995（3）：19－21.

［2］ 刘振艳，刘振义，宋继田，等.凹凸变化壁面强化传热机理与传热性能的研究［J］.节能技术，2007，25（4）：305－308.

［3］ Burgess N K，Ligrani P M.Effects of dimple depth on channel Nusselt numbers and friction factors［J］.Journal ofHeatTransfer，2005，127（8）：839－847.

［4］ Hwang S D，Cho H H.Heat transfer enhancement of internal passage using dimple／protrusion［C］／／13th Int.Heat transfer conference，Sydney，Australia，HTE24，2006.

［5］ Samad Abdus，Lee Ki－Don，Kim Kwang－Yong.Multiobjective optimization of a dimpled channel for heat transfer augmentation［J］.HeatandMassTransfer，2008，45（2）：207－217.

［6］ 王定标，姜逢章，杨丽云，等.蜂窝板传热元件的数值模拟［J］.郑州大学学报：工学版，2008，29（1）：5－9.

［7］ 丹宇.丁胞流道内流动传热的数值模拟研［D］.重庆：重庆大学，2004.

［8］ 姜逢章.蜂窝板传热元件的性能研究［D］.郑州：郑州大学，2010.

［9］ 何雅玲，王煜，雷永刚.丁胞型强化换热管，中国：200910022779.6.［P］.2010－11－15.

［10］ Xie G N，Sundrn B.Numerical predictions of augmented heat transfer of all internal blade tip－wall by hemispherical dimples［J］.IntemationalJournalofHeatandMass Transfer，2010，53：5639－5650.

［11］ Yang Y T，Wei T C，Wang Y H.Numerical study of turbulent slot jet impingement cooling on a semi－circular concave surface［J］.InternationalJournalofHeatand MassTransfer，2011，54：482－489.

［12］ Chang S W，Liou H F.Heat transfer of impinging jet－array onto concave－and convex－dimpled surfaces with effusion［J］.InternationalJournalofHeatandMassTransfer，2009，52：4484－4499.

［13］ Xing Y F，Weig and B.Experimental investigation of impingement heat transfer on a flat and dimpled plate with different cross flow schemes［J］.InternationalJournalof HeatandMassTransfer，2010，53：3874－3886.

［14］ Koonlaya K，Ricardo F M.Heat transfer correlations of perpendicularly impinging jets on a hemispherical－dimpled surface［J］.InternationalJournalofHeatandMass Transfer，2010，53（15）：3045－3056.

［15］ Momayez L，Dupont P，Delacourt G，eta1.Genetic algorithm based correlations for heat transfer calculation on concave surfaces［J］.AppliedThermalEngineering，2009，29：3476－3481.

［16］ Sharif M A R，Mothe K K.Parametric study of turbulent slot－jet impingement heat transfer from concave cylindrical surfaces［J］.InternationalJournalofThermalSciences，2010，49：428－442.

［17］ 王福军.计算流体力学［M］.北京：清华大学出版社，2004：113－143.

［18］ Webb R L，Eekert E R G.Application of rough surfaces to heat exchanger design［J］.InternationalJournalofHeat andMassTransfer，1972，15（9）：1647－1658.

［19］ 王晓霞.酒窝板换热特性的实验研究［D］.西安：西安科技大学，2008.

［20］ 过增元.换热器中的场协同原则及其应用［J］.机械工程学报，2003，39（12）：1－9.

［21］ 梁珍祥.凹坑凸胞板式换热器性能的数值研究［D］.郑州：郑州大学，2012.