利用改进的遗传算法求解约束优化问题*

陈 磊， 霍永亮

(1.重庆师范大学 数学学院，重庆 401331；2.重庆文理学院 数学与财经学院，重庆 永川 402160)

0 引 言

一般地，约束优化问题被定义为

minf(x)

s.t.gi(x)≤0，i=1，2，…，p

(1)

hi(x)=0，i=p+1，…，m

其中x=(x1，x2，…，xn)∈Rn，x∈F⊆S⊆Rn，集合F为目标函数的可行域，集合S为目标函数的搜索空间。定义的x每个分量的上下界，即aj≤xj≤bj，1≤j≤n。

这个系统在许多科学领域都有运用，如物理[1]，飞机设计[2]，天文学[3]，化学[4]，生物[5]等。为了解决这些问题，许多算法被提出，如：Lagrange multiplier methods[6]，Trust region methods[7]，Interval methods[8]，methods that utilize artificial neural networks[9]，derivative free optimization methods[10]等。最近几年，基于种群的随机搜索算法被提出来求解约束优化问题，随机算法有GAS[11]，Particle Swarm optimization[12]和differential evolution[13]。它们的优势有如下3点：算法不要求目标函数是可微和连续的；算法不需要计算函数梯度；算法能避免陷入局部最优解。

本文对传统遗传算法提出了3种改进策略：对终止准则的改进；对交叉和变异操作的改进；对一种局部搜索算法运用的改进，即周期性的运用一种局部搜索算法。在此首先提出实数编码遗传算法并做出详细地描述。其次，提出改进策略并用改进算法测试一系列优化问题。最后，用此算法的测试结果与算法C-SOMGA和DONLP2的结果进行比较，得出数值实验结论。

1 改进算法

1.1 适应度函数

算法用一种处罚策略把有约束优化问题转化为无约束优化问题。当一个初始解是不可行时，根据约束惩罚对它的适应度进行处罚。任意给定个体x的适应度函数F(x)如下：

(2)

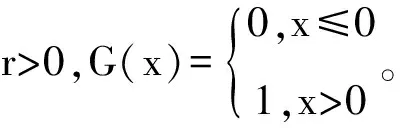
1.2 改进的变异操作

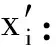
(3)

其中，c1、c2均为正常数，r1、r2都是在[0，1]上的随机数。

1.3 运用局部搜索

运用局部搜索寻找每Kls代的局部最优个体xl，其中Kls是一个被定义的常数，其表示需要多长时间运用一次局部搜索，运用局部搜索的目的是改进xl的函数值，并加快改进算法的收敛速率。

1.4 改进的终止准则

Kaelo和Ali的终止准则主要是种群中的最好个体和最坏个体的差异来决定是否终止。改进的终止准则也合并了Kaelo和Ali的终止准则，其表示如下：

或iter>ITERMAX或

(4)

其中，ε=10-4，σiter表示每一次迭代中每代的最好个体的方差，σlast表示迭代过程中第一次发现最好个体fl的方差。

1.5 算法步骤

算法初始化目标函数中K个有界个体组成的集合，并反复地对个体利用改进的遗传操作直到终止准则被满足。算法的主要步骤如下：

步骤1 假设算法参数。K为个体数量；ITERMAX为最大遗传代数；ps为选择率；pm为变异率；pc为交叉率；pl为局部搜索率。

步骤2 令iter=0，初始化K个个体并把它们保存在集合X={x1，x2，…，xn}。在式(1)的可行域F里，随机初始化每个个体xi。

步骤3 运用适应度函数计算每个个体的适应度(适应度函数见1.1)。

步骤4 对种群运用改进的交叉和变异操作(交叉和变异操作见1.2)。

步骤5 从种群中随机选择一些个体并对它们运用局部搜索技巧，最终用我们选择的个体代替种群中适应度较差的个体(局部搜索见1.3)。

步骤6 令iter=iter+1。

步骤7 如果满足终止准则(终止准则见1.4)，算法停止，否则算法进入步骤3。

2 数值实验

用改进算法测试两个相关文献的测试问题，并得出改进算法的测试结果。

2.1 测试函数

Levy[14]：

其中，a=2，b=0.25。目标函数的全局最小值fmin=-1.872 9。

Salkin[15]：

其中，1≤x1≤4，80≤x2≤88，30≤x3≤35，145≤x4≤150，0≤x5≤2。目标函数的全局最大值fmax=320。

2.2 测试结果

改进算法用表1给定的参数测试了测试函数，改进算法的测试结果见表2。算法C-SOMGA的测试结果来自文献[11]，而算法DONLP2的测试结果引用文献[16]。算法C-SOMGA的测试结果见表3，算法DONLP2的测试结果见表4。

表1 改进算法中参数的取值

表2 改进算法的测试结果

表3 算法C-SOMGA的测试结果

表4 算法DONLP2的测试结果

由此可见，改进算法结果是有效的。一方面，改进算法在平均值和标准差两个方面优于算法C-SOMGA，而且几乎每一个目标函数都能够求出全局最优解。另一方面，算法DONLP2在计算问题(LEVY)时，虽然改进算法在函数估计数量方面没有算法DONLP2好，但是改进算法在平均值和标准差两个方面优于算法DONLP2。

3 结束语

本文结合遗传算法求解全局最优解的特点，提出了求解约束优化问题的改进的遗传算法。首先，根据Particle Swarm优化算法的速率更新提出了改进的变异操作，利用改进的变异操作保证种群多样性，避免算法出现早熟现象。其次，为了加快算法的收敛性，算法周期性的运用一种局部搜索算法改进每代种群中最优个体的函数值(适应度)。最后，以渐近的思想给出了一种新的终止准则，并根据已有的终止准则结合新的终止准则判断算法是否终止，从而节约算法计算的时间。利用改进的遗传算法测试了一系列著名问题，结果表明对于大多数问题而言，算法在函数估计数量、平均值和标准差3个方面是成功的。未来将研究一些更有效地交叉变异操作和其他局部搜索方法来改进遗传算法求解优化问题。

参考文献：

[1] CHAO Y，MEZAA J，WANGA L. A constrained optimization algorithm for total energy minimization in electronic structure calculations[J].Journal of Computational Physics，2006，217(2)：709-721

[2] LEE K，EYI S. Transonic airfoil design by constrained optimization[J].Journal of Aircraft，1993，30(6)：805-806

[3] SEELOS F，ARVIDSON R. Bounded variable least squares-application of a constrained optimization algorithm to the analysis of TES Emissivity Spectra [C].34th Annual Lunar and Planetary Science Conference，2003(3)：17-21

[4] WILLIAMS G，DUGAN J，ALTMAN R. Constrained global optimization for estimating molecular structure from atomic distances[J].Journal of Computational Biology，2001，8(5)：523-547

[5] Bertram J. Constrained optimization in human walking：cost minimization and gait plasticity[J].Journal of Experimental Biology，2005，208(6)：979-991

[6] BERTSEKAS D，OZDAGLAR A. Pseudonormality and a Lagrange multipliertheory for constrained optimization[J].Journal of Optimization Theory and Applications，2004，114(2)：287-343

[7] POWELL M，YUAN Y. A trust region algorithm for equality constrained optimization[J].Mathematical Programming，1990，49(1-3)：189-211

[8] MARKOT M，FEMANDEZ J，CASADO L，CSENDES T. New interval methods for constrained global optimization[J].Mathematical Programming，2005，106(2)：287-318

[9] WALTER E，STEFEN H，STANISLAW H. Neural networks for constrained optimization problems[J].International Journal of Circuit Theory and Applications，1993，21(4)：385-399

[10] LUCIDI S，SCIANDRONE M，TSENG P. Objective-derivative-free methods for constrained optimization[J].Mathematical Programming，2002，92(1)：37-59

[11] DEEP K，DIPT I. Aself-organizing migrating genetic algorithm for constrained optimization[J].Applied Mathematics and Computation，2008，198(1)：237-250

[12] HE Q，WANG L. A hybrid particle swarm optimization with a feasibility-based rule for constrained optimization[J].Applied Mathematical and Computation，2007，186(2)：1407-1422

[13] BECERRA R，COELLO C. Cultured differential evolution for constrained optimization[J].Computer Methods in Applied Mechanics and engineering，2006，195(33-36)：4303-4322

[14] LEVY A，MONTALVO A. The tunneling algorithm for global optimization of functions[J].SIAM Journal of Scientific and Statistical Computing，1985，6(1)：15-29

[15] SALKIN H. Integer Programming，Edison Wesley Publishing Com [Z].Amsterdam，1975

[16] SPELLUCI P.An SQP method for general nonlinear programs using only equality constrained sub-problems[J].Mathematical Programming，1998，82(3)：413-448