基于多体动力学的滚子链式运输机建模与分析

王秀文 张 飞 邹中生 刘 歌

(中冶赛迪上海工程技术有限公司 上海200940)

基于多体动力学的滚子链式运输机建模与分析

王秀文①张 飞 邹中生 刘 歌

(中冶赛迪上海工程技术有限公司 上海200940)

基于多体动力学理论建立滚子链式运输机多体动力学仿真模型，对链轮的扭转振动情况进行了分析，同时通过频域分析得到整机系统的坎贝尔图和模态能量分布图，并对整机系统潜在共振点进行甄别。研究结论可为滚子链传动运输系统的动态分析与设计提供一定借鉴。

滚子链 多体动力学模型 扭振分析 频域分析

滚子链具有耐磨、耐疲劳、耐腐蚀和承载能力强等优点而被广泛应用在动力传递和物料运输等机械工程领域，如冶金设备中的滚子链式运输机。滚子链由多个柔性链节组成，具有高度挠性，在运动过程中存在着多边形效应、啮合冲击作用及横向振动的问题，因此滚子链系统的动力学分析将更加复杂，很多研究者都对其进行深入地研究。根据建模方法的不同滚子链系统动力学模型可分为如下三类：弹性弦模型、耦合集中质量模型(离散模型)和多体动力学模型[1-5]。由于弹性弦模型和耦合集中质量模型不能准确地反映链条本身特有的结构离散特性和链节转动惯量等因素对系统的影响[6-8]，而多体动力学模型具备前两者的优点即：链节之间采用柔性的铰接方式并考虑了链节本身转动惯量及链轮与链节啮合时啮合刚度等因素的影响，能够精确地反映出系统的振动特性及链条—链轮之间冲击，因此文中采用多体动力学理论建立滚子链式运输机仿真模型，并依据模型分析了滚子链式运输机在运行过程中的振动响应特性。

1 滚子链式运输机几何模型

滚子链式运输机主要由机架、传动电机、短节距滚子链和链轮组成。传动电机和链轮安装在机架上，电机驱动一根通长轴实现一排链轮和链条运动，钢板堆垛在链条上最终实现传递垛料的功能，是一种常见的用于运输钢板的冶金设备。几何模型如图1所示。

图1 链式运输机几何模型

2 滚子链多体系统力学模型

滚子链多体系统建模过程中需建立以下假设：①链节间由拉压弹簧和扭转弹簧组成柔性铰连接；②链节和链轮是刚性体；③相邻的链节连接处无间隙，如图2所示。

图2 滚子链多体模型

取链节i质心相对于惯性坐标系的平移坐标ri和转动坐标θi作为链节的广义坐标，即

链节i在铰接点Oi处的位移、速度和加速度为

Ai—链节i的方向余弦阵；

链节i的角速度和角加速度为

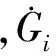
滚子链系统总动能为

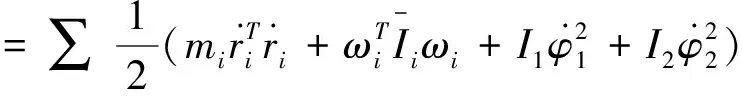
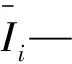
根据多体系统的广义力计算方法，可得系统拉格朗日方程：

Qi=Qit+Qir+Qic

式中Qit—链节间的拉压弹簧广义力；Qir—链节间的扭转弹簧广义力；Qic—滚子与链轮间的接触广义力。

3 滚子链多体动力学仿真模型

多体系统的联系方式称为系统的拓扑构型，简称拓扑[9]。拓扑结构是多体系统(Multi-body System)的一个基本概念，也是多体系统(MBS)建模重要前提。建立多体动力学模型之前需确定模型的拓扑图，拓扑图可以很详尽的反映各部件的连接关系、自由度、约束和受力情况。拓扑模型的好坏不仅牵涉到模型建立的正确与否，而且关乎到模型规模的大小和复杂程度。评估系统拓扑结构的好坏，主要以系统的自由度和一阶状态量最小为原则[10-11]。在闭环系统自由度(DOF)，系统的一阶状态数量(FOS)和独立铰链的数量(NIndependent Joints)的关系为

如果系统自由度(∑DOFsystem)数量最少，则整个系统的一阶状态数量(∑FOSsystem)也是相对最少，意味着整个多体系统的微分方程最少。

滚子链式运输机动力学模型的拓扑图如图3所示。

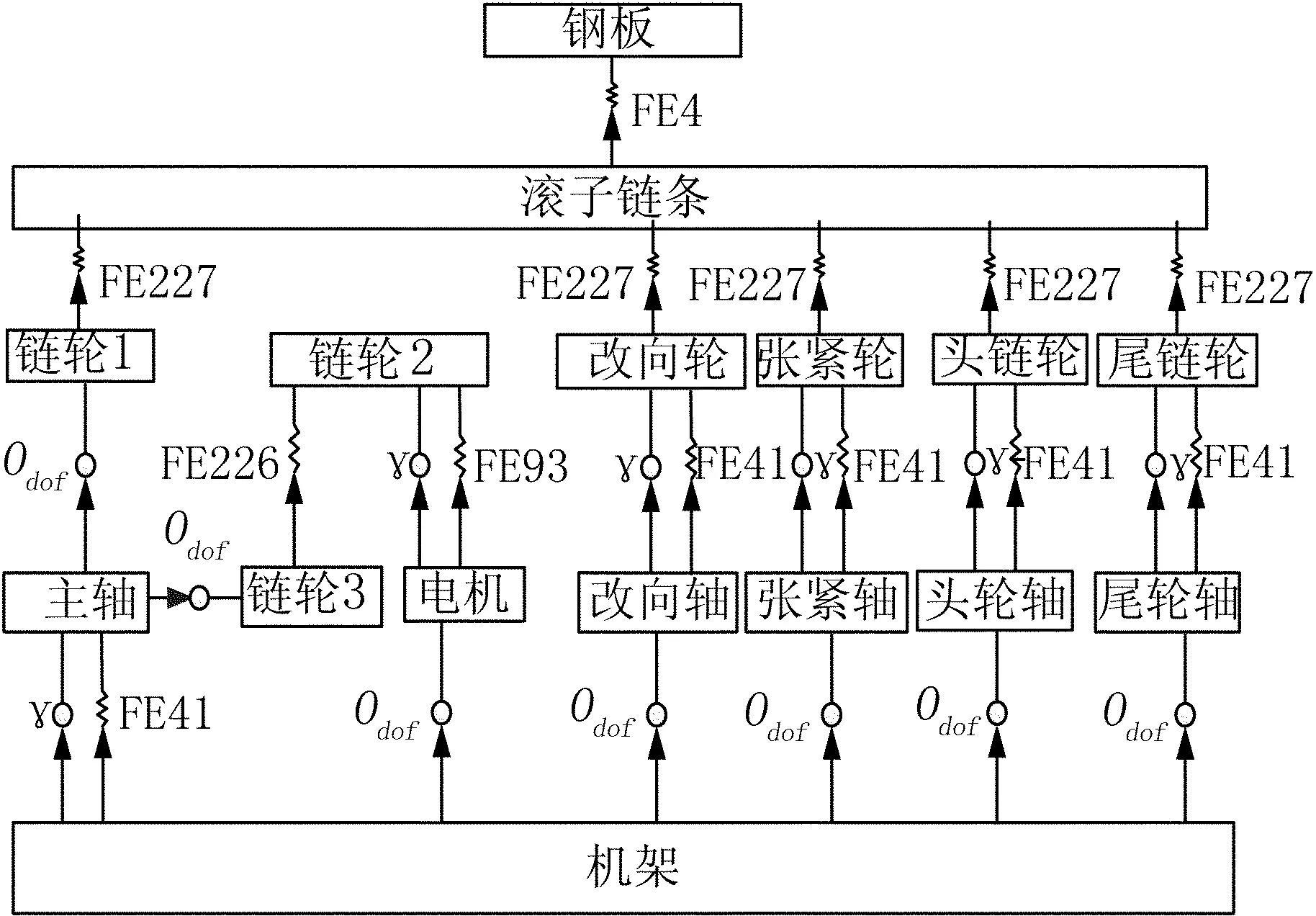
图3 链式运输机拓扑结构图

从拓扑图中可以看出通过226号力元和相应的柔性铰接方式建立滚子链，滚子链与链轮之间通过227号力元来建立相互啮合作用，从而形成完整的滚子链系统；通过4号力元来描述钢板和链条之间的相互作用；通过93号力元来表示电机对整个系统的驱动作用，γ表示绕Z轴的自由度；轴承则采用FE41号力元来描述，该力元可以给定两个Marker点(标志点)之间六个自由度的线性或非线性刚度和阻尼系数，可完整的描述轴承的约束支撑作用。

根据拓扑图和力学模型建立链式运输机系统模型，如图4所示。

图4 滚子链式运输机仿真模型

4 计算结果

滚子链链号为16B-3(三排短节距滚子链)，模型中相关参数设置如表1所示。

表1 仿真参数设置

图5 主从动链轮扭振分析

4.1 链轮扭振分析

图5给出了链式运输机主动链轮转速为31r/min条件下，滚子链运输系统主/从动链轮扭转振动的时域响应与频域分析情况。

从时域分析可以发现，主动链轮的扭转振动加速度较大(冲击峰值高)，表明主动轮受啮合冲击作用影响较大。而从动链轮扭转振动加速度较小，受啮合冲击作用较小，无明显的振动现象。从频域分析中可以发现，主/从动链轮扭转振动中的主要激励成分是转速31r/min条件下的链轮啮合激励频率，激励频率值为10.3Hz。除基本激励频率外，系统中还存在一系列谐波振动成分，其值为主激励频率的整数倍。另外，主动链轮扭转振动中各阶谐波振动成分均比较明显，从动链轮扭转振动中各阶谐波成分不明显。说明链轮与链节之间的啮合冲击更能够激起主动链轮扭转振动中的高阶谐波振动成分。

4.2 频域(模态能量)分析

本节的主要目的是通过频域分析，甄别滚子链式运输机整机系统潜在共振点。频域分析的第一步是利用坎贝尔(Campbell)图找出外界激励频率和固有频率的交点，此交点处的激励频率可能是引发链式运输机发生共振的外界激励频率；第二步通过绘制整机固有频率的能量图进一步甄别坎贝尔图上频率交点是否为整机系统的潜在共振点。

坎贝尔(Campbell)图反映系统在旋转过程中自身固有频率与外界激励频率之间的关系，可用来判定系统发生共振时的外界激励频率，绘制Campbell图是频域分析的基本方法。系统达到动平衡后进行模态分析，可得到整机固有频率，如表2所示。

表2 整机固有频率(Hz)

链轮转速在15r/min～31r/min，主/从动轮齿数均为20，因此系统啮合激励频率为5Hz～10.3Hz。根据上述计算的固有频率和激励频率绘制坎贝尔图。

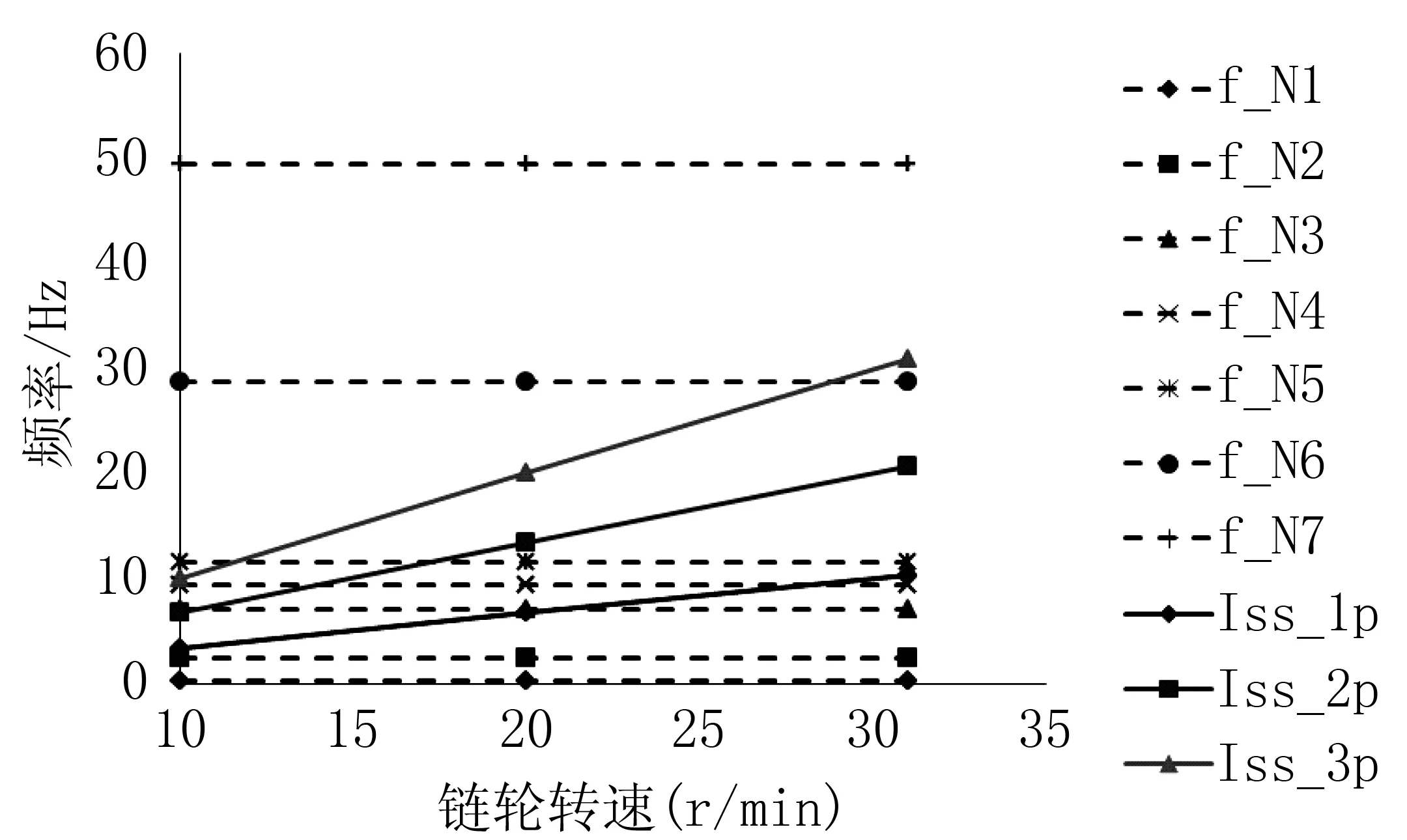
图6 坎贝尔(Campbell)图

如图6所示与激励频率有交点的固有频率为f_N3～f_N6分别对其进行模态能量分布图绘制(每个模态能量趋势一致以f_N3为例)，如图7所示。

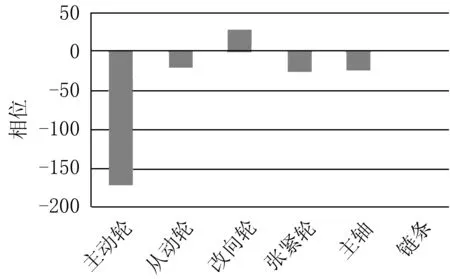
图7 模态能量分布图(f_N3)

根据坎贝尔图和模态能量图甄别潜在共振点。潜在共振点甄别依据：坎贝尔图中交点处的激励频率所对应的零部件与该交点处固有频率的能量分布图中能量比大于20%的零部件属于同一速度级，则视该激励频率为潜在共振频率。

通过f_N3～f_N6的模态能量图发现，振动能量主要在滚子链条上，能量比均超过90%；但系统中滚子链由234节链节组成，每个链节的能量比均很小(未超过1%)，因此链轮的啮合激励频率不是系统的潜在共振频率。

5 结论

研究了基于多体动力学理论的滚子链运输机的动力学建模与仿真问题，得出以下结论：

1)通过扭转振动分析得出链式运输机的主动链轮的扭转振动加速度较大，受啮合冲击作用影响较大，而从动链轮受啮合冲击作用较小。同时啮合冲击能够激起主动链轮扭转振动中的高阶谐波振动成分。

2)通过频域(模态能量)分析方法得到整机的固有频率和外界激励频率，并绘制整机系统的坎贝尔图和模态能量分布图，从而验证链轮激励频率不是系统的潜在共振点。

[1]Choi W, Johnson G E.Vibration of Roller Chain at Low Medium and High Operation Speeds[J]. Mechanical Engineering and Applied Mechanics, 1998, Vol.252(1):21-52.

[2]Wang K W.On the Stability of Chain Drive Systems under Periodic Sprocket Oscillations[J]. Journal of Vibration and Acoustics, 1992, Vol.114(2):119-126.

[3]Wang K W.Vibration Analysis of Engine Timing Chain Drives with Camshaft Torsion Excitations, In: Proceedings of the 1991 Noise & Vibration Conference May 13-16, Traverse City, MI, USA, 1991, 244:196-207.

[4]胡胜海,郭彬等.考虑完整齿廓的滚子链系统Sim Mechanics建模与仿真[J].吉林大学学报，2012，Vol.43(4):958-963.

[5]Zheng H, Wang Y Y, Quek K P.A Refined Numerical Simulation on Dynamic Behavior of Roller Chain Drives[J]. Shock and Vibration, 2004, Vol.11(5-6):573-584.

[6]刘晓论，荣长发，张格，郑志峰.高速滚子链传动动力学分析[J].农业机械学报(增刊)，1998:177-181.

[7]Kim M S, Johnson G E.Multi-body Dynamic Model to Predict the Behavior of Roller Chain Drives at Moderate and High Speeds, IN: Proceedings of the 14thBiennial Conference on Mechanical Vibration and Noise, Albuquerque, NM,USA, September 19-22, 1993:247-468.

[8]许立新，杨玉虎，刘建平等.链传动啮合冲击理论分析及有限元模拟[J].天津大学学报，2010, Vol.43(2):132-137.

[9]洪嘉振.计算多体系统动力学[M].北京：高等教育出版社，2009:9-11.

[10]廖炳荣，方向华.SIMPACK动力学分析基础教程[M].成都：西南交通大学出版社，2008:34-37.

[11]陆佑方.柔性多体动力学[M].北京：高等教育出版社，1996:233-242.

BasedontheMulti-BodyDynamicsModelingandAnalysisoftheRollerChainTransferMachine

Wang Xiuwen Zhang Fei Zou Zhongsheng Liu Ge

(CISDI Shanghai Engineering Technology Co., Ltd, Shanghai 200940)

Based on multi body system and mechanical model, built multi body dynamic model of roller chain conveyor and analyzed twist vibration of chain wheel. Meanwhile, campbell diagram and model energy distribution were derived. Further analysis of latent resonance was carried out. The result of this research can be used as for reference of dynamic analysis and design of roller chain transmission system.

Roller chain Multi-body dynamics model Torsional vibration analysis Frequency domain analysis

王秀文，男，1986年出生，毕业于重庆大学机械设计及理论专业，硕士研究生，工程师

TG333.3

A

10.3969/j.issn.1001-1269.2014.05.003

2014-05-24)