基于键合空间理论的直线闭合弹带启动特性
邓致远,林圣业,姜铁牛,王茂森,管红根,戴劲松
(1.南京理工大学 机械工程学院, 南京 210094; 2.国营第152厂, 重庆 400071)
1 引言
直线闭合弹带是自动炮无链供弹装置中常用的供弹结构,通过构件间相互碰撞作用完成各种规定动作,与弹链供弹相比,供弹过程不需要除链、排链等动作,且具有传动阻力小等优点[1]。同时与普通链传动不同,闭合弹带是一个受结构所限的极少齿数的传动且传动距离远,多边形效应影响显著,链节由链节导引约束,链节间连接松散,快速启停冲击大,高速运动过程中振动剧烈。
文献[1-7]利用了多刚体动力学建立了弹链动力学模型,但其动力学分析常局限于机械结构,忽视了该系统是一个机电耦合的系统,且闭合弹带系统是无链供弹系统,与有链供弹系统不同,其传动的动态特性对满足系统的工作非常重要,上述模型的建立方法是以分析力学及弹性力学为基础,对于多种能量形式并存的系统,不能用统一的方式实现系统动力学的建模,这在很大程度上制约了该类系统的动力学自动建模与仿真[2]。文献[8]和文献[9]分别建立了粗糙球形表面和圆柱形表面的接触力学模型,结合在多体动力学模型中的接触运动副处理,该文献提供了新思路。文献[10]中利用Adams和Easy5仿真软件联合仿真建立了供输弹系统机电液耦合仿真。王中双等[11-13]利用向量键合图解决了机电一体化建模及计算机仿真问题。戴劲松[14-15]将系统动力学键合图理论应用于火炮机构设计,并将其发展为键合空间理论,得到了以结点为中心的键合空间模型自动推导方法,可以用统一的方式实现多能域并存系统的建模。
本文以键合空间理论为基础,通过特征结点提取的方式,在模型中描述了不同构件的主要尺寸特征,并以Hertz理论为基础描述了不同构件间的接触碰撞关系,建立了准确的直线闭合弹带键合空间模型,并建立了实验装置验证模型的正确性和合理性。在弹链的运动过程中,链节间隙、闭合弹带长度等因素变化产生的振动和冲击会对链节的动力学特性有较大影响,在闭合弹带的运转过程中会导致闭合弹带系统发生卡弹、电机启动力矩过大等现象,分析了直线闭合弹带链节间隙对电机启动力矩特性的影响。
2 直线闭合弹带系统的基本描述
图1为直线闭合弹带常见的结构形式,其主要由若干链节(弹托)、链轮、链节导轨、电机及弹丸支撑架组成。

图1 直线闭合弹带常见结构示意图Fig.1 Top view of a linear closed shell chain
针对该通用结构,通过简化结构的外观尺寸,建立如图2所示的平面闭合弹带结点模型,使其适用于键合空间的模型建立形式。

图2 平面闭合弹带系统结点模型示意图Fig.2 The junction model of a plane closed projectile belt system
2.1 链节(弹托)特征提取与模型简化
闭合弹带的启停、稳定运行的动力学特性受链节形状及物理特性的影响,不同弹链形状及形式对闭合弹带系统的动力学特性影响较大,因此结点模型中需保留单个链节的物理特征信息,如图3(a)所示,提取闭合弹带的主要连接点及质心特征,将闭合弹带的所有受力情况,确定为闭合弹带模型4个功率输入点的受力,在传动过程中,由于C点为销轴与E处的孔配合,且链轮只与销轴接触,因此,4点的接触关系如图3所示。其中A点为单个链节的质心位置,B点为链节与弹丸之间接触受力点,C点为该链节与上一个链节的转动副受力点,D点为链节与链节导轨内侧的接触受力点,E点受3个力,分别为该链节与下一个链节的转动副受力、该链节与链节导轨外侧接触受力及该链节与链轮之间的接触受力,各接触力大小由接触深度判定,因此,在计算过程中不发生接触的2个节点之间相互作用力为零。
基于上述简化模型,定义两链轮轴心所在直线为全局坐标系x轴,如图3(b)所示,添加链节形状参数α为C、E两特征点与链节坐标系x轴正方向的夹角,使得该模型可适用于不同链节模型,同时定义链节位置参数θ为单个链节在全局坐标系下的方向角,如图3(c)所示。即可得到BCDE点与A点之间的速度v、角速度ω关系为:
(1)
式(1)中:q=b,c,d,e;lb、lc、ld、le分别表示点B、C、D、E至点A的距离。

图3 链节模型特征示意图Fig.3 Simplified schematic diagram of chain model features
2.2 链轮与链节啮合特征描述
图4表示了链轮与链节的啮合。链节在链轮处主要通过与链轮两端销轴的接触限制链节并传递扭矩,在本模型中采用2个接触描述链轮与链节的约束情况,分别为:① 链节端点与虚线链节轨道之间的接触描述啮合时的径向力F1;② 链节与简化十字形链轮之间的接触描述链节所受法向力F2。

图4 链轮与链节啮合示意图Fig.4 Sprocket and chain meshing feature description diagram
F1和F2的求解,除上述链节结构参数外,还需定义直线闭合弹带的结构参数(见图4)。两链轮轴心所在直线为全局坐标系x轴,两链轮轴心连线的中垂线为y轴。定义两链轮中心位置分别为(x1,0)和(-x1,0),轨道半径为r1,两链轮转角分别为θ1和θ2,轮齿齿数为n,以图4所示左侧链轮为例,可确定链节轨道函数l(x)为:
(2)
链节各结点的坐标均为在全局坐标系下的坐标,以单个链节为例,第i个链节的结点E坐标为(xei,yei)与轨道函数l(x)的侵入深度,如式(3)所示,即结点坐标至轨道函数的距离。
(3)
链条结点E(xe,ye)与链轮轮齿的侵入深度,如式(4)所示,即结点E(xe,ye)至最近一条链轮直线的距离函数。
(4)
式(4)中,δθi表示链节与接触链轮拨齿之间的角度差。
在此,利用取最小值来获得二者的角度差,同时n表示链轮的齿数,θx(j)表示每个链轮齿在全局坐标系下的指向角度,θE表示每个链节结点E与链轮中心连线与x轴正方向的夹角。δθi表达式为:

(5)
(6)
(7)
2.3 平面闭合弹带接触力及间隙特征描述
根据接触力学理论将法向接触力简化为等效弹簧阻尼模型,其广义表达式为:
(8)

根据Hertz接触理论,可推导出接触刚度计算式为:
(9)
式(9)中:R为接触点综合曲率半径;E为两接触构件的综合弹性模量。
在模型中,链节与链节导引之间的接触为两圆柱体交叉接触,该类接触等同于一个球体与一个平面接触;而链节与链节之间、链节与弹丸之间、链节与链轮之间两中心轴平行的圆柱体之间的接触,其作用力与接触深度呈线性比例关系,即:

(10)
式(10)中,L为两接触体接触线长度。
接触阻尼模型可采用Lankarani和Nikravesh根据能量损耗给出的基于法向变形量的非线性滞后阻尼模型[16],即:
(11)
式(11)中:K为接触刚度;e为碰撞恢复系数;ν为接触点碰撞速度;δ为接触点的法向变形量;a为非线性阻尼的幂指数。
在此基础上,加入接触副间隙判定函数,即:
(12)
式(12)中:l为两接触弧面圆心距离;e为两接触面运动副单边间隙;H(x)为间隙判定矩阵,当x>0时H(x)为单位矩阵,当x<0时H(x)为零矩阵。
在链节与其他零件的接触过程中,两接触面之间是相互滑动的,因此将切向接触力定义为库伦摩擦模型。其表达式为:
Ff=-μdFnsgn(ν)
(13)
式(13)中:Ff为啮合点的滑动摩擦力;μd为动摩擦因数;Fn为接触面正压力;ν为啮合点的相对滑移速度。
3 直线闭合弹带的键合空间模型
依据键合空间理论,建立闭合弹带系统键合空间模型的方法和步骤,在上述模型的基础上绘制闭合弹带键合空间模型,如图5所示。闭合弹带键合空间模型由多个相同链节构成,若需建立一个链节数为n的闭合弹带模型,只需将若干单个链节键和空间模型首尾相连即可,依据键合空间的符号规则,所有容性元件C、惯性原件I、阻性原件R、摩阻元件H及势源Se均以所连接的共流节1脚标做区分,图5中,1(i,1)代表第i个链节的1号共流节,其余共流结标号依此类推,1(i,1)表示第i个链节C节点与第i-1个链节E节点之间转动副的流空间,1(i,2)为与第i个链节对应的弹丸流空间,1(i,3)为第i个链节质心的流空间,1(i,4)为第i个链节E节点的流空间,1(i,5)为第i个链节D节点的流空间,1(i,6)、1(i,7)分别表示第i个链节E节点与驱动链轮、从动链轮的相对速度流空间,1(i,8)为第i个链节B点与对应弹丸的相对速度流空间,1(9)和1(10)分别为主动链轮和从动链轮的流空间;容性元件C(i,1)为第i个链节C节点与第i-1个链节E节点接触力的弹性部分,C(i,4)为第i个链节E节点与链节导轨外侧接触力的弹性部分,C(i,5)为第i个链节D节点与链节导轨内侧接触力的弹性部分,C(i,6)为第i个链节E点与驱动链轮接触力的弹性部分,C(i,7)为第i个链节E点与从动链轮接触力的弹性部分,C(i,8)为第i个链节B点与弹丸接触力的弹性部分;阻性元件R(i,1)为第i个链节C节点与第i-1个链节E节点接触力的阻尼部分,R(i,4)为第i个链节E节点与链节导轨外侧接触力的阻尼部分,R(i,5)为第i个链节D节点与链节导轨内侧接触力的阻尼部分,R(i,6)为第i个链节E节点与驱动链轮接触力的阻尼部分,R(i,7)为第i个链节E节点与从动链轮接触力的阻尼部分,R(i,8)为第i个链节B节点与弹丸接触力的阻尼部分,R(i,10)为从动链轮转动副的阻尼部分;摩阻元件H(i,4)为第i个链节E节点与链节导轨外侧的摩擦阻力,H(i,5)为第i个链节D节点与链节导轨内侧的摩擦阻力;惯性元件I(i,2)为第i个链节所对应弹丸的质量,I(i,3)为第i个链节质心的质量,I(9)为驱动电机转子的转动惯量,I(10)为从动轮的转动。
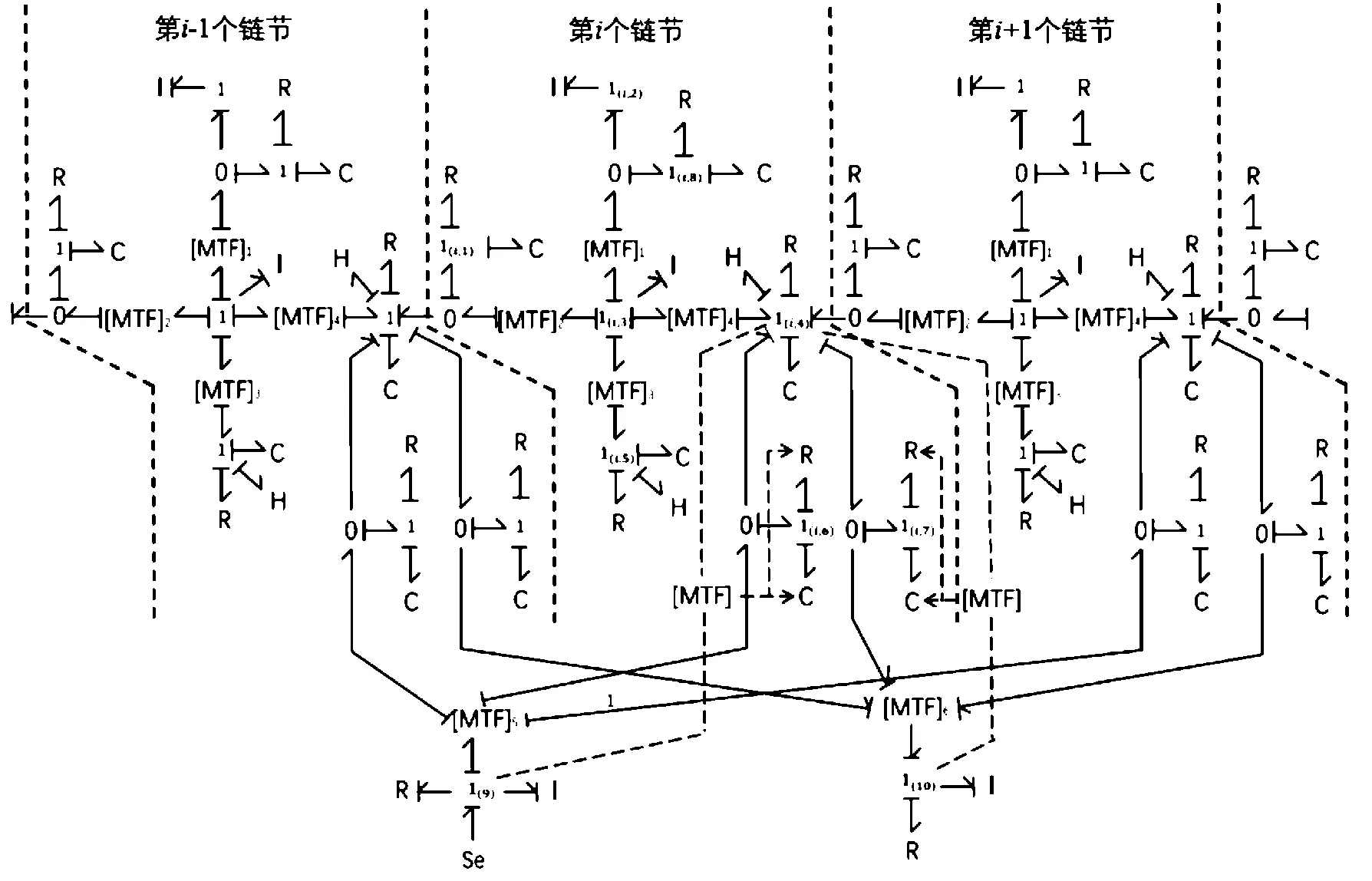
图5 直线闭合弹带键合空间模型示意图Fig.5 Bond space picture of a linear closed shell chain
惯量;[MTF]1、[MTF]2、[MTF]3和[MTF]4分别为第i个链节质心速度与其B点、C点、D点、E点速度之间的传递关系,[MTF]5、[MTF]6代表驱动链轮、从动链轮扭矩与各链节E点之间相互作用力的关系。
依据键合空间模型,因果关系主要以驱动链轮的Se输入为入口,以各节点的R元件为出口,同时单个链节能量流动主要由链节质心流向链节的4个节点,能量在链节间的流动均以图5中初定方向为正方向,在计算中符号仅代表能量流动方向。同时依据图5中惯性元件和容性元件的因果关系,即以确定系统的动力学状态方程为:

(14)
式中q表示对应速度流空间的流在时间长度上的积分,即位变;p表示对应势在时间长度上的积分,即动量变量。在上述键合空间模型中使用[MTF]元件表示链节结点之间的势流关系,在推导过程中,各节点位置的独立计算会导致随着计算步数的增加链节节点相对位置畸变,因此B、C、D、E节点位置改为由A节点位置获得,使每一步计算中链节结点位置相对固定,例如在方程中对q(i,4)进行计算时不采用迭代积分的方法,而根据刚体几何关系由质心位置确定。因此式(14)为以p(i,2)、p(i,3)、p(i,9)、p(i,10)为自变量的一阶微分方程组。
4 实验
4.1 实验装置介绍
为验证仿真模型的正确性和有效性,在直线闭合弹带键合空间模型的基础上,以某型直线闭合弹带为对象,对上述模型进行实验验证,实验原理图如图6所示。由工控机控制伺服电机达到目标转速,在伺服电机输出轴与直线闭合弹带系统输入轴之间安装扭矩传感器,以测量电机扭矩。

图6 直线闭合弹带系统实验原理示意图Fig.6 Schematic diagram of a linear closed shell chain system
该实验主要仪器及设备有:伺服电动机及其驱动器;斜齿硬齿面减速器;T10F扭矩法兰传感器及其采集盒;双十字万向节驱动轴;运动控制卡ADT8940;工控机;电机传感器工装、实验台架工装、传动轴过渡工装,实验装置如图7所示。

图7 直线闭合弹带系统实验装置示意图Fig.7 Test device diagram of a linear closed shell chain system
在该闭合弹带装置实验系统中,考虑到各传动尺寸及万向节对该电机的输出功率影响较大,因此,在扭矩传感器安装时并不将其之间连接在电机主轴上,而是采取将传感器直接连接在尺寸轴与链轮轴之间的方式,直接获取链轮轴的输入扭矩。
4.2 模型验证
搭建实验装置并采集目标转速为50 r/min时的转速和扭矩曲线,并依据表1参数进行仿真计算,为将采集到的数据与仿真数据对比,得到链轮速度实验与仿真对比曲线和转矩实验与仿真对比曲线分别如图8和图9所示。
表1 计算参数
Table 1 Parameters

参数值弹性模量E/ GPa206弹链尺寸/mmb=17/c=e=26/d=14综合曲率半径R/mm4.2非线性弹性力幂指数n1碰撞恢复系数e0.9非线性阻尼的幂指数a1.5弹链质量m/mg0.235 8惯性矩J/(kg·m-2)478×10-6

图8 直线闭合弹带系统实验和仿真转速曲线

图9 直线闭合弹带系统实验和仿真扭矩曲线Fig.9 Comparison curve of torque between tests and simulation of the linear closed elastic belt system
由图8和图9可以看出,键合空间动力学模型仿真数据与实验数据趋势基本一致,表2为仿真和实验的力矩曲线主要特征值对比,其中稳定后最大力矩绝对误差为-0.03 N·m,相对误差为-1.54%,稳定后平均力矩绝对误差为0.07 N·m,相对误差为5.94%,二者相对误差均在10%以内,能够较好地描述闭合弹带系统稳定工作时的状态,表明上述键合空间模型可以正确描述出闭合弹带系统的传动机理。其中稳定后平均力矩主要受链节与导轨之间和链轮轴与基架间的摩擦力影响,其仿真数据大于实验数据原因在于模型中的摩擦系数选取较大(未考虑润滑及磨合情况),其二稳定后最大力矩仿真数据略小于实验数据,表明仿真数据相对实验数据振动程度更小,其原因主要在于键合空间模型中的接触力模型误差所导致。

表2 实验数据与仿真数据 Table 2 Comparison of test data and simulation data
综上所述,上述键合图模型可以正确描述闭合弹带系统,该模型具有正确性和有效性,在后续计算分析中,以该模型代替实物物理模型进行分析。
5 不同间隙下直线闭合弹带启动特性分析
在直线闭合弹带系统运行过程中,链节的振动对整体系统影响较大,尤其在弹链较长的闭合弹带系统和极少齿数的直线闭合弹带系统中,链节的抖动问题更为严重,同时在对航炮等空间有限的自动机供弹时,减小供弹系统体积,减小系统所需启动力,能够大大增加自动机供弹系统的可靠性。考虑到链节间隙不仅可以影响链传动过程中的张紧力,同时也会影响链节直线段的振动特性等因素,利用上述仿真模型,对链节间隙大小在直线闭合弹带系统启动特性中的影响进行探究。通过改变链节间隙大小,仿真计算不同间隙下直线闭合弹带电机启动力矩如图10所示。

图10 不同间隙下启动力矩曲线Fig.10 Starting torque curve under different clearance
由图10可知,当链节间隙μ=0 mm时,启动力矩峰值出现在0.009 54 s,峰值为-6.335 17 N·m,随着间隙的不断增大,当链节间隙μ=0.2 mm时,启动力矩峰值出现在0.054 48 s,峰值为-3.749 34 N·m,在仿真数据范围内,直线闭合弹带系统链节间隙越小,电机启动力矩峰值越大,电机达到峰值扭矩的时间越短,但随着间隙的逐步增大,在间隙由μ=0.15 mm增大至μ=0.2 mm的情况下,启动力矩峰值只减小了0.166 04 N·m,随着间隙的增大,间隙增量对启动力矩峰值大小的影响逐步减小,但对力矩峰值出现时间的影响依然明显。
仿真结果说明:随着链节间隙的逐步增大,驱动电机启动过程中的冲击强度逐渐减小。其原因在于增大链节间隙,链轮需要更大的运动角以带动整个链节运动,因此链节间隙将n个链节同时驱动的过程变成多个链节逐步驱动的过程,此过程在一定程度上可以减小直线闭合弹带系统对驱动电机的性能要求,减小电机体积和供弹系统体积。但过大的链节间隙则会影响闭合弹带系统的紧凑性,同时,链节间隙过大也会影响链轮驱动链节时的啮合情况。
图11为链节间隙分别为0.05 mm、0.1 mm、0.15 mm和0.2 mm下电机稳定力矩曲线。

图11 不同间隙下电机稳定力矩曲线Fig.11 Motor stable moment curve under different clearance
由图11可知,当链节间隙为0.05 mm和0.1 mm时,电机扭矩有明显的周期性波动,且在波动过程中会周期性产生峰值,峰值大小随链节间隙的增大逐步减小。
由于链传动受多边形效应影响,其传动过程中不可避免地产生周期性波动,在直线闭合弹带系统中,拨弹轮齿数越少,多边形效应越明显,因此,极少齿数直线闭合弹带抖动比较剧烈,由上述仿真结果可知,适当增大链节间隙,在一定程度上可以减小周期性峰值大小,为减小链节抖动提供了新思路。
6 结论
本文以键合空间理论为基础建立了直线闭合弹带的动力学模型,对直线闭合弹带系统运行过程中的不同接触碰撞进行分类并进行结点化描述,在Hertz接触模型的基础上加入间隙因子,获得机电耦合状态下的直线闭合弹带动态特性,并以某直线闭合弹带实验装置为基础,验证了模型的正确性,分析了不同链节间隙下直线闭合弹带系统的启动特性,得到以下主要结论:
1) 基于键合空间理论的直线闭合弹带系统动力学模型计算结果与实验结果一致,验证了本文所提出模型的正确性与有效性。
2) 适当增大直线闭合弹带系统链节间隙,能够有效减小电机启动时的冲击,一方面有利于直线闭合弹带系统在与自动机的匹配过程中,通过采用调节间隙的方式选取力矩更小的电机,减小空间占用,同时,更小的启动力矩峰值可以增加闭合弹带系统启动的平稳性。
3) 适当增大直线闭合弹带系统链节间隙可以明显减小电机扭矩的周期性波动峰值,可以为减小直线闭合弹带系统运行过程中的振动提供新的思路。

