智能车辆局部避障轨迹规划研究
姚 芳,郑 帅,吴正斌
(1.河北省电磁场与电器可靠性重点实验室(河北工业大学),天津 300132;2.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学), 天津 300132;3.中国科学院大学 深圳先进技术研究院, 广东 深圳 518055)
1 引言
避障轨迹规划是智能车辆主动安全技术中的重要一环[1-4],其目的是寻求车辆在当前车道环境及车辆运动约束条件下的最优避障运动解[5-6]。当车道前方存在障碍车辆,如驾驶员未及时作出转向判断决策,则需主动安全系统快速根据前方障碍车辆位置、车速等信息规划并跟踪避障轨迹[7-8]。在局部避障轨迹规划策略中,需保证车轮侧偏角、横向加速度等车辆动力学参数控制在约束范围内,以保证规划轨迹的可靠性及稳定性[15],在此基础上提升车辆避障过程驾驶舒适性是轨迹规划策略的重要研究方向。
在智能车辆轨迹规划策略的研究中,人工势场法的应用较为广泛,其中,文献[9]基于道路和障碍车辆的信息构建了一个三维危险潜力场,然后生成实时无碰撞轨迹用于轨迹跟踪。文献[10]在轨迹规划模块中设计了非对称车道势场函数范围,并得到无碰撞路径。因此,人工势场法可有效应用于全局工况下的避障轨迹规划决策。
但是在局部避障过程中,为了提高避障过程的车辆稳定性,还需考虑如侧向加速度、质心侧偏角和轮胎侧偏角等车辆动力学约束,因此,现有研究成果将人工势场法与MPC策略相结合,提高避障轨迹规划可靠性。2种算法的结合研究中,主要可分为2个研究方向,其一为通过人工势场法求解二次规划参考轨迹,随后通过MPC算法重规划出带约束的理想避障轨迹[11]。其二为通过人工势场法,优化设计MPC策略目标函数中的避障惩罚项,提升避障可靠性。其中,文献[12]定义了斥力势场的横向安全范围,并将斥力函数作为避障惩罚项引入MPC目标函数中。文献[13]提出可穿越型障碍物及不可穿越型障碍物斥力势场,并将合斥力函数作为避障惩罚项引入MPC目标函数中。但文献[12-13]中,障碍车辆斥力势场的作用范围均为圆型区域,当车辆完成避障动作,在相邻车道安全行驶时,仍受到斥力函数作用,使得轨迹规划层求解出远离障碍车辆的目标点,影响车辆稳定性及避障安全性。对此,文献[14]将斥力势场作用范围改进为椭圆型区域,得到更加合理的规划轨迹。但是,当自主车辆处于大幅转向过程中,持续受到向外的斥力,则可能导致车辆转向过度或车身失稳。因此,固定范围的斥力势场不能很好地适用于自主车辆的避障决策中。
对此,为提升避障惩罚项的灵活性、可靠性,文中根据自主车辆的避障动态过程,定义碰撞风险区域及转向失调风险区域,并结合人工势场理论,对自主车辆所受引斥力进行优化设计,并将引斥合力引入轨迹规划层目标函数作为避障惩罚项。在保证整车质心侧偏角、侧向加速度、轮胎侧偏角远离约束边界的同时,得到规划轨迹最优解,提高整车行驶稳定性与舒适性。
2 基于MPC的避障路径规划
2.1 点质量模型
在避障轨迹规划中,为便于理论分析及控制器设计,忽略轮胎受力,并将整车简化为点质量模型,采用的点质量模型如图1所示。
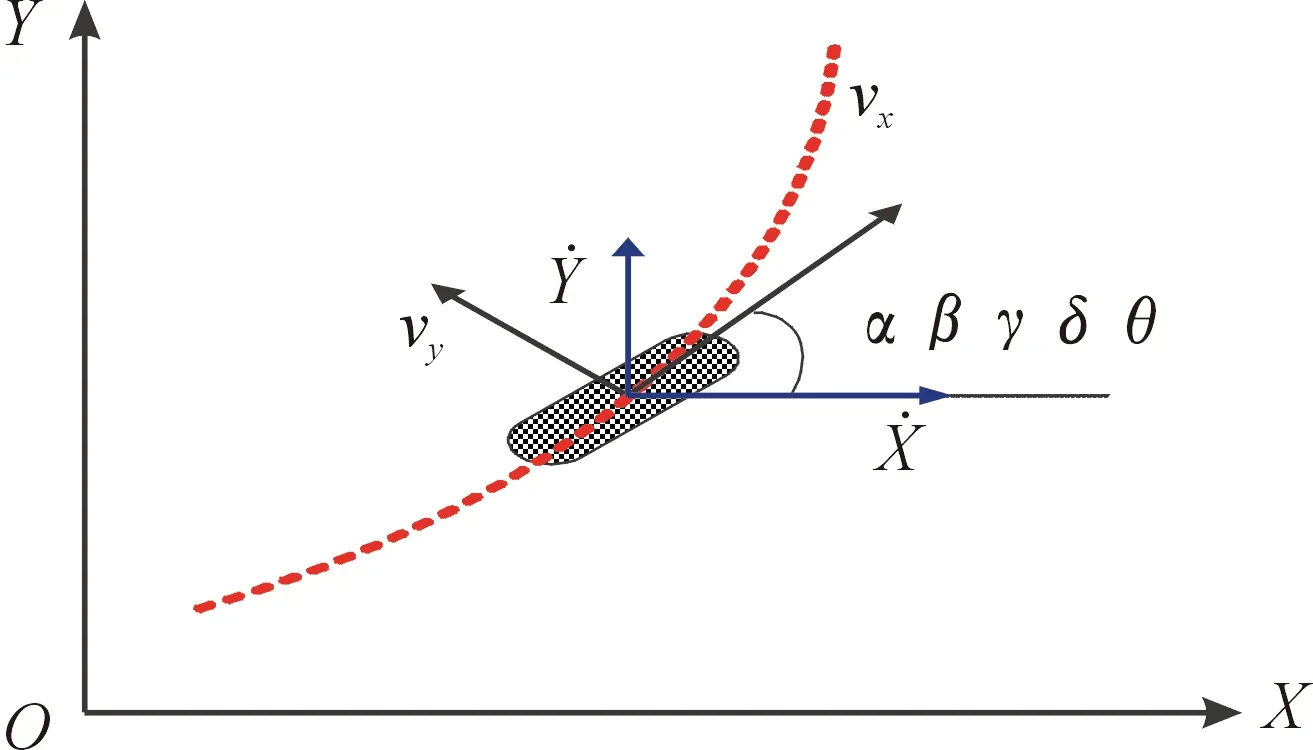
图1 点质量模型示意图Fig.1 Point quality model
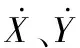
此时车辆运动模型可表示为
(1)
(2)
(3)
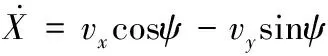
(4)
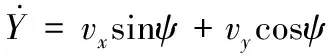
(5)
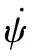
2.2 非线性MPC避障轨迹规划控制器
将式(1)~式(5)离散化,可得
vx(k+1)=vx(k)+Tax
(6)
vy(k+1)=vy(k)+Tay
(7)
(8)
X(k+1)=X(k)+T[vx(k)cos(ψ(k))-vy(k)sin(ψ(k))]
(9)
Y(k+1)=Y(k)+T[vx(k)sin(ψ(k))+vy(k)cos(ψ(k))]
(10)
其中:T为离散时间;k为离散递推整数;Vy(k)、Vx(k)、ψ(k)、X(k)、Y(k)均表示当前时刻对应相关变量。
假设车辆避障过程中纵向状态保持稳定,即vx为常数、ax=0此时有
vx(k+1)=vx(k)
(11)
选取侧向加速度ay为非线性MPC轨迹规划控制量,选取Vy(k)、Vx(k)、ψ(k)、X(k)、Y(k)为非线性MPC轨迹规划状态变量,定义非线性MPC轨迹规划控制输出函数为
η(k+i|t)=Fi[η(k|k),ay(j)]
(12)
式中,

(13)
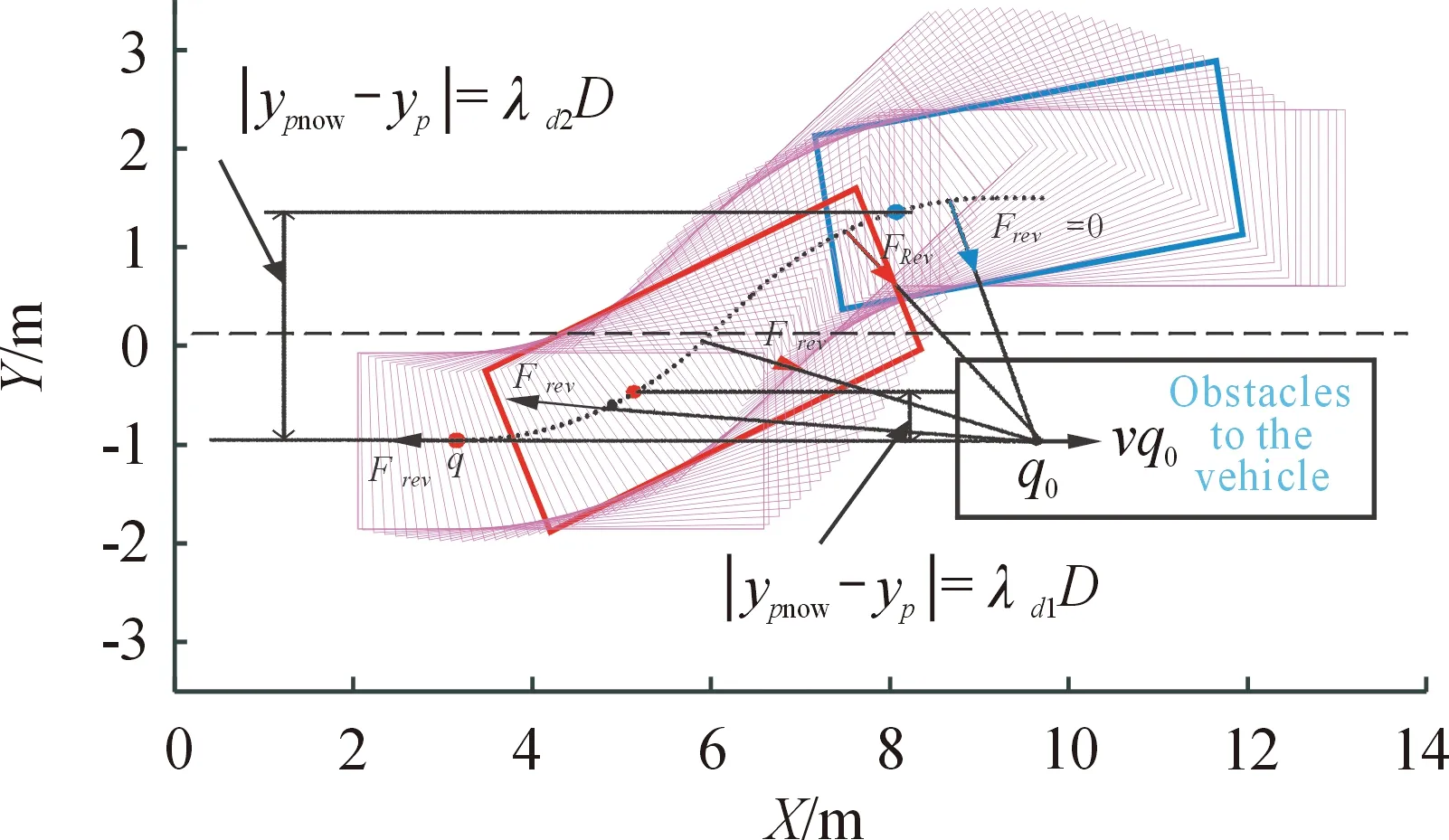
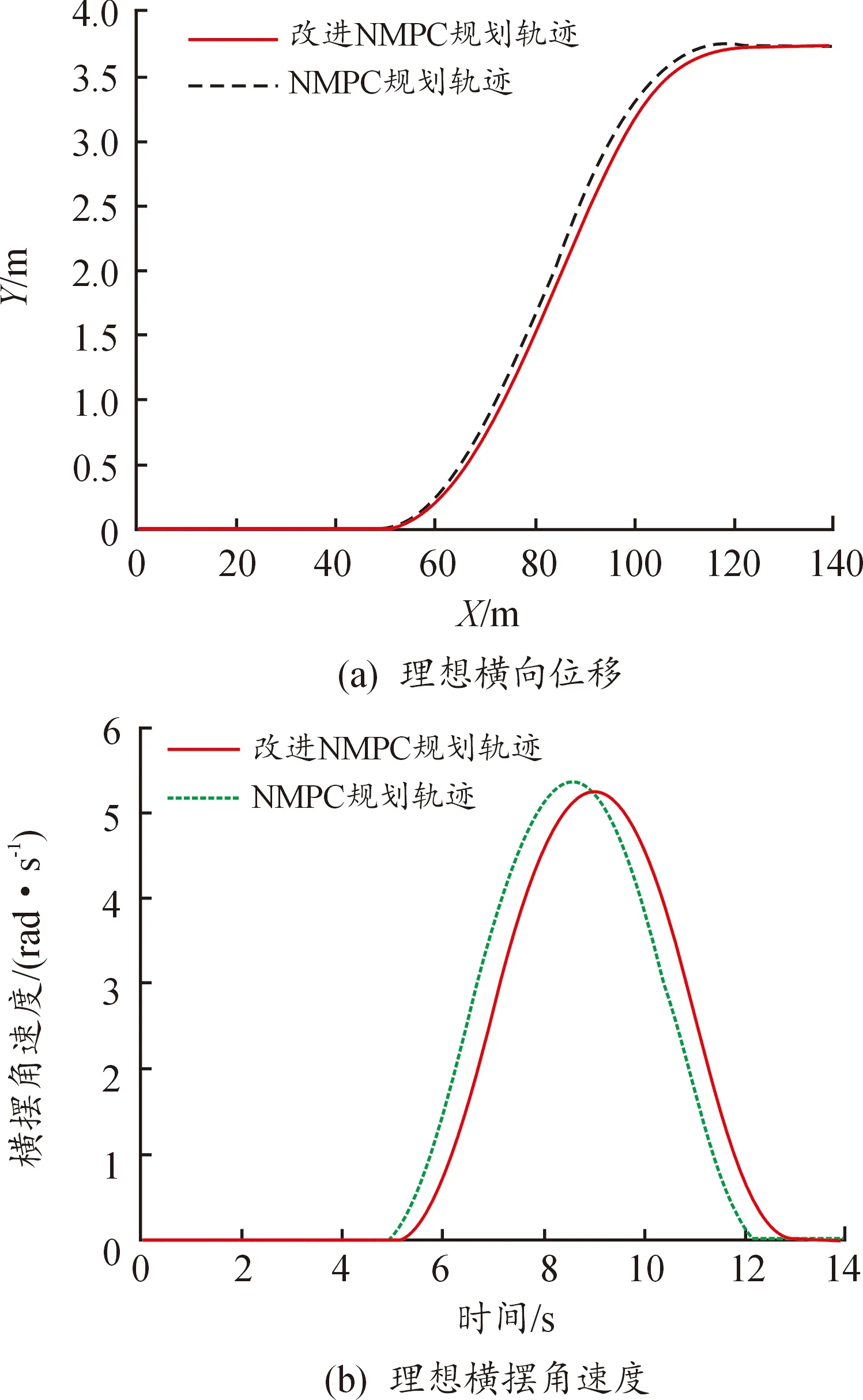
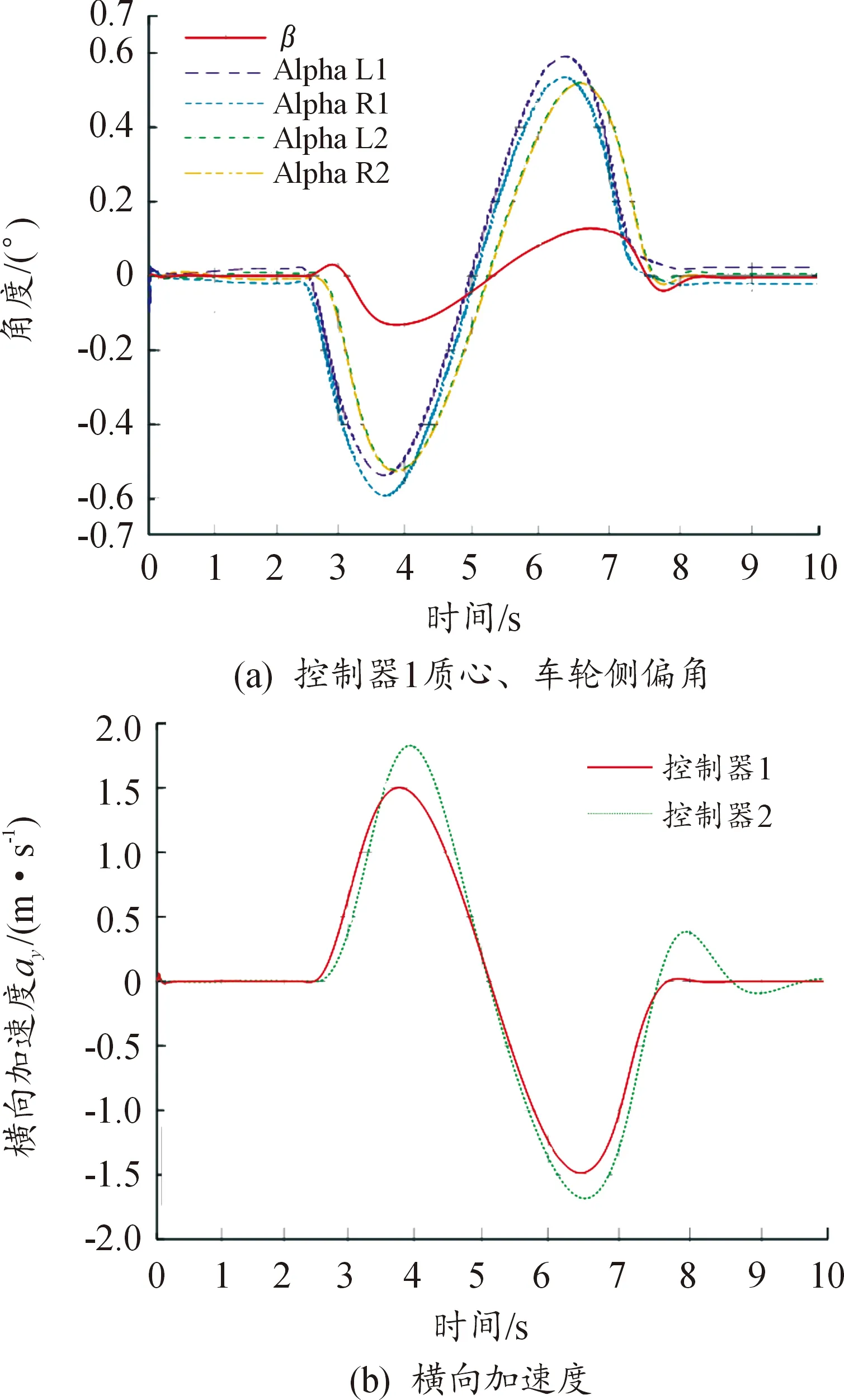
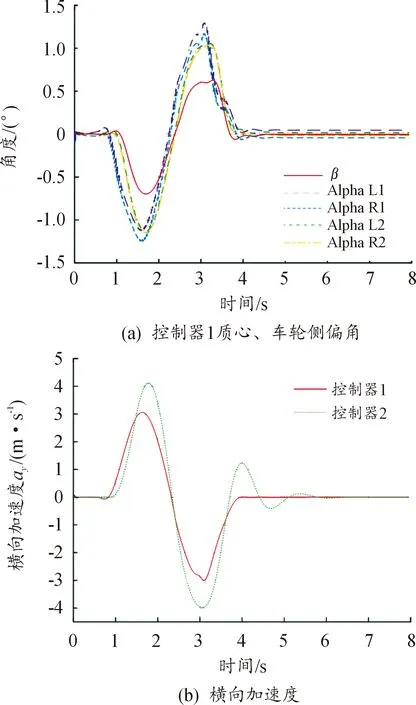
式中:Np为预测时域;Nc为控制时域,且Nc (14) 最终得非线性MPC轨迹规划控制器的预测表达式为 (15) 式中:η(k+i|k)为k时刻时,k+i时刻离散化后的车辆状态变量的预测值。 为使临时路径尽可能缩小与全局静态参考路径的跟踪误差,同时考虑侧向加速度及其增量约束、道路边界约束以保证避障过程车身转向稳定性及避障可靠性,设计非线性MPC轨迹规划控制器的目标函数为 (16) 式中:Qi、Rj分别为输出量、控制量加权矩阵,其中i=1,2,…,Np,j=1,2,…,Nc。 3.1 改进车辆局部避障速度引斥函数 实际工况中,障碍车辆以一定速度行驶,若忽视障碍车辆的相对运动状态,则可能导致避障失败。本文车辆避障过程所受速度斥力情况如图2所示。 图2 避障车辆所受速度斥力示意图Fig.2 Schematic diagram of the velocity repulsion of a barrier avoidance vehicle 图2中,Frev为相对速度斥力,q为车辆当前质心位置,q0为障碍车辆当前质心位置,D为初始时刻车辆质心至道路中线的纵向距离,λd1为无碰撞风险因子,λd2为无转向失稳风险因子,且0<λd1<1、λd1<λd2<2,yp为初始时刻车辆质心的纵向位置,D=|yp|,ypnow为避障车辆当前质心纵向位置,车辆质心纵向位置变化量为|ypnow-yp|。 当车辆避障过程中,定义碰撞风险临界时刻(如图2中红色线框位置),此时避障车辆边界距障碍车辆边界距离最短,此刻|ypnow-yp|=λd1D;定义转向失调风险临界时刻(如图2中蓝色线框位置),此时|ypnow-yp|=λd2D。 定义速度引斥函数为 (21) 式中:Urev为速度斥力势能;krev>0为速度斥力势能增益;q、v分别为车辆当前质心位置、车速;q0、v0分别为障碍车辆当前质心位置、车速;ρ(q,q0)为q至q0的距离;ρ0为斥力势场作用范围。 经过重新定义的速度引斥函数特点为: 1) 需保证ρ(q,q0)小于斥力场范围ρ0时斥力函数才有可能作用; 2) 需保证两车质心距离qq0变化量为负数时,即两车相对距离不断减小时斥力函数才有可能作用; 3) 当车辆处于碰撞风险区域,即|ypnow-yp|<λd1D,速度引斥函数有可能作用,此时表现为斥力;当辆处于转向失调风险区域,即λd1D<|ypnow-yp|<λd2D,这时速度引斥函数有可能作用,此时表现为引力,助力车身回稳,避免转向过度;当|ypnow-yp|超过λd2D,速度引斥函数不起作用,避免避障车辆回稳时转向过度。 当(1)(2)(3)点同时满足时,则速度引斥函数作用,此时速度引斥力为 (22) 沿用3.1节设计思想,定义障碍车辆引斥势场函数为 (23) 式中:Urep为障碍车辆引斥势能;k1>0为障碍车辆引势能增益。 对应障碍车辆引斥力为 (24) 综上,改进避障车辆引斥函数及所受引斥力为 (25) 将改进后障碍物引斥力函引入式(16)中,同时引入松弛项ρε2,保证二次规划存在最优解,最终可得避障轨迹规划层目标函数为 (26) 式中,Qi、Rj为权重矩阵。 联合仿真试验中,设计自主车辆车速分别为36 km/h、72 km/h、108 km/h,障碍车辆于横向位置100 m处静止。基于障碍车辆引斥合力的NMPC轨迹规划控制器控制效果如图3—图5所示。 图3 36 km/h轨迹规划控制器输出效果曲线Fig.3 Output of the 36 km/h trajectory planning controller 图4 72 km/h轨迹规划控制器输出效果曲线Fig.4 Output of the 72 km/h trajectory planning controller 图5 108 km/h轨迹规划控制器输出效果曲线Fig.5 Output of the 108 km/h trajectory planning controller 由图3—图5可见,当车辆开始避障时,自主车辆处于碰撞风险区域,2个控制器规划轨迹相近。当自主车辆躲开障碍车辆后,处于无碰撞风险且车身回正区域时,改进的NMPC控制器规划出平缓轨迹,避免车身回正急转向操作时转向不足从而出现侧翻的问题,且车辆横摆角速度峰值更小,车身稳定性更佳。避障过程横向位移单位时间增量小于传统NMPC横向位移单位时间增量,即避障过程所需车辆侧向加速度较小,车辆稳定性及驾驶舒适性均更佳。 为验证基于障碍车辆引斥合力NMPC轨迹规划层的有效性,建立轨迹规划及跟踪双层控制CarSim/Simulink联合仿真平台,观测四轮侧偏角及侧向加速度变化情况。将本文所设计的基于障碍车辆引斥合力NMPC轨迹规划层命名为控制器1,传统NMPC轨迹规划层命名为控制器2,试验结果如图6—图8所示。 由图6—图8可知,在横向加速度观测值中,采用控制器1的车辆在保证避障安全的前提下,低中高车速下的横向加速度峰值更小,驾驶舒适性更佳。36~108 km/h的避障车辆四轮侧偏角范围为-1.3°<α<1.3°,质心侧偏角范围为0°<β<0.6°,满足动力学约束,避免了车身甩尾及打滑等危险状况发生。 图6 36 km/h避障效果曲线Fig.6 36 km/h obstacle avoidance results 图7 72 km/h避障效果曲线Fig.7 72 km/h obstacle avoidance results 图8 108 km/h避障效果曲线Fig.8 108 km/h obstacle avoidance results 引入速度引斥力及障碍车辆引斥力,定义了避障风险区域及转向失调风险区域,据此改进自主车辆所受引斥合力作用区域,优化惩罚避障项的作用效果,在保证避障安全的前提下,提升驾驶舒适性及操纵稳定性。将基于障碍车辆引斥合力的惩罚避障项引入非线性MPC轨迹规划策略的目标函数中,CarSim/Simulink试验表明了本轨迹规划策略的有效性。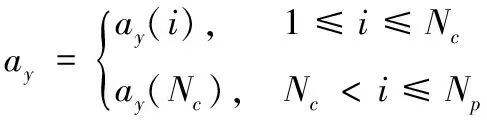
3 基于障碍车辆引斥力的NMPC轨迹规划控制器设计
3.2 改进障碍车辆引斥力

3.3 基于引斥合力的局部避障轨迹规划目标函数
4 CarSim/Simulink联合仿真



5 结论

