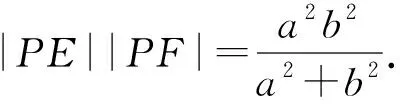对2014年福建省数学高考解析几何试题的探究

●

(商城第二高级中学 河南信阳 465350)

2014年福建省数学高考理科第19题是一道平面解析几何中常见的直线与双曲线位置关系的综合题.该题突出了解析几何的学科思想，如数形结合、运动变化、用代数方法研究几何等.同时对考生的分析、推理、转化的数学逻辑思维能力提出了更高要求.如何在解析几何中避免繁杂、冗长的计算，即简化运算，特别是洞察题目所给信息的内在联系，是解决问题的关键.

(1)求双曲线E的离心率.

(2)如图1，O为坐标原点，动直线l分别交直线l1，l2于点A,B(A，B分别在第一、四象限)，且△OAB的面积恒为8.试探究：是否存在总与直线l有且只有1个公共点的双曲线E？若存在，求出双

曲线E的方程；若不存在，请说明理由.

图1

第(1)小题的解答：

该题的重点在第(2)小题.

1 题意的初步理解

(1)“动直线l分别交直线l1，l2于点A,B(A，B分别在第一、四象限)”，这就形成一个△OAB，此时动直线l与双曲线E的右支相离、相交、相切均有可能，且这样的动直线有无穷多条.

(2)由“△OAB的面积恒为8”知面积为定值，此时动直线l与双曲线E的位置关系如何呢？

(3)“是否存在总与直线l有且只有1个公共点的双曲线E”，由于动直线不可能与渐近线平行，因此l与双曲线E相切，据此可大胆猜想：满足条件的直线与双曲线相切且△OAB的面积恒为定值(本题的答案为8).此时，切点P相对于点A,B的位置关系是怎样的呢？

在题目未完全求解之前，存在诸多不确定因素有待解决.解题不仅仅是一个确认数学结论的过程，而且也是一个理解和发现数学结论的过程.

2 解题的具体方法

考虑1如何设动直线l的方程.

考虑2如何表达S△OAB，这既有一个策略选择问题，也有一个运算量问题.

…

下面给出第(2)小题的解法：

图2

从而

t2=4|1-4m2|=4(1-4m2).

(4m2-1)y2+8mty+4(t2-a2)=0,

又4m2-1<0,直线l与双曲线E有且只有1个公共点当且仅当

Δ=64m2t2-16(4m2-1)(t2-a2)=0,

即

4m2a2+t2-a2=0,

亦即

(1-4m2)(a2-4)=0,

得

a2=4.

3 对题目的探究

对题目所蕴涵的深层次关系进一步探究，可获得一些重要结论:

双曲线的渐近三角形有如下结论：

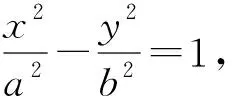
b2x2-a2y2=a2b2,

对y求关于x的导数得

2b2x-2a2yy′=0,

则在点P处的导数为

k=y′|x=x0,

从而

因此过点P的切线方程为

化简得

即

结论2双曲线上一条切线和渐近线所围成的三角形的面积是一个常数.

图3

切点为P(x0,y0).由结论1知，过点P的切线方程为

(1)

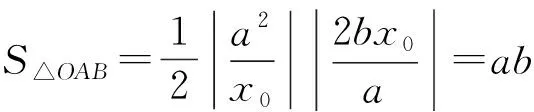
利用结论2,可获得第(2)小题的另一种解法：

结论3点P为线段AB的中点，即|PA|=|PB|.

证明因为

所以

同理可得

因此点P为线段AB的中点，即|PA|=|PB|.

结论4|OA||OB|=a2+b2.

本题第(2)小题还有如下解法:

解法3由已知双曲线E的渐近线为y=±2x知tan∠AOx=2,显然∠AOx为锐角，从而

则 sin∠AOB= sin2∠AOx=

即

a2+b2=20，

又b=2a,解得a2=4，b2=16.

以上4个结论能很好地解决“题意的初步理解”中的疑问.事实上，还可由此得到另外2个有用的性质，此处证明略.