年年岁岁题相似 岁岁年年意不同——2014年浙江省数学高考理科“传承题”评析

●

(湖州市第二中学 浙江湖州 313000)

2014年高考已经落下帷幕，浙江省数学高考理科卷的命题很有特色，对学生的综合要求较高.在许多核心知识点的考查方式上体现了命题者独具匠心的一面，其中有不少试题的风格和2013年有很大的相似之处，解题思路也很有关联性，笔者暂且称之为“传承题”，取沿袭、承接、创新之意，对比摘录如下，与大家一起评析.

1 “传承题”之一：三视图题，从“截”到“拼”

例1若某几何体的三视图(单位：cm)如图1所示，则此几何体的体积等于______cm2.

图1 图2

(2013年浙江省数学高考理科试题第12题)

例2某几何体的三视图(单位：cm)如图3所示，则此几何体的表面积是

( )

A.90 cm2B.129 cm2C.132 cm2D.138 cm2

图3 图4

(2014年浙江省数学高考理科试题第3题)

评析三视图是新课改后增加的内容，在近几年的高考中属于热点问题之一.此类试题让学生关注从局部到整体的展开形式，以三视图、直观图，以及点、线、面的位置关系来帮助学生完善思维结构，发展空间想象能力，并在几何直观的基础上，初步形成对空间图形的逻辑推理能力，最终让学生经历“实物模型—三视图—直观图”这一相互转化的过程来认识几何体.

例1的答案为24，该几何体的直观图是直三棱柱在上面截去一个三棱锥(如图2所示).例2的答案为D，该几何体的直观图是直三棱柱和长方体的组合体(如图4所示).这2道题有很多共通之处:首先难度上都定位为中档题，但实际考查下来对学生来说是易错题，另外在模型的设置上都对学生的空间想象能力提出了更高要求.不管是例1的“截”还是例2的“拼”，学生对此类“变形几何体”的直观认知都存在一定的难度.在实际教学中，教师可以让学生尝试以长方体作为载体来研究，以“切拼橡皮泥”的可操作模式来更好地获得直观感受.例2的设置体现了命题者对发展高中学生核心应用能力和空间想象能力的持续关注.教师若在平时的教学中注重研究，关注学生相关能力的培养，而不是盲目做题，则学生解决此类问题应该不是难事.

2 “传承题”之二：平面向量，背景一致

( )

A.∠ABC=90° B.∠BAC=90°

C.AB=ACD.AC=BC

(2013年浙江省数学高考理科试题第7题)

( )

A.min{|a+b|,|a-b|}≤min{|a|,|b|}

B.min{|a+b|,|a-b|}≥min{|a|,|b|}

C.max{|a+b|2,|a-b|2}≤|a|2+|b|2

D.max{|a+b|2,|a-b|2}≥|a|2+|b|2

(2014年浙江省数学高考理科试题第8题)

评析平面向量是高考的必考内容之一，近几年向量试题的出题风格相对比较灵活，入口宽，深入难，其解法主要有2个途径：一是侧重几何表示的几何法;二是侧重坐标表示的代数法.

例3和例4都考查了向量的同一个几何背景，即平行四边形法则及相关衍生性质.例3的答案为D，可以巧用极化恒等式来求解(其解法甚多，也多见于各种文章，具体过程不再赘述)，此种解法可充分体现数形结合的“精妙”.例4的答案为D，其中a+b，a-b，a和b的几何意义是平行四边形中的边和对角线.例4是平行四边形定理的一个应用，即

max{|a+b|2,|a-b|2}.

从解答中可以发现，例4的设置体现了命题者对平面向量这一经典数学概念的重视，正如章建跃教授所说：高中平面向量实质上主要是几何的应用.

3 “传承题”之三：线性规划，“参数”依旧

(2013年浙江省数学高考理科试题第13题)

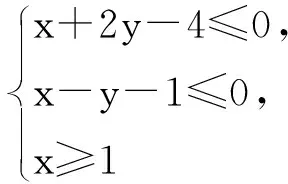
(2014年浙江省数学高考理科试题第13题)

评析线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,高中数学的线性规划实际是非常特殊的多元函数在简易定义域上的一个简单性质——求最值的问题.教材的定位是让学生初步了解运筹学的部分内容，为学习高等数学打下基础，同时培养了学生数形结合、转化化归的基本数学思想.这部分内容因其出题灵活，同时易与其他知识点交汇而在高考中越来越受到重视.

图5

4 “传承题”之四：压轴填空，殊途同归

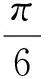
(2013年浙江省数学高考理科试题第17题)

图6

例8如图6，某人在垂直水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面的射击线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小.若AB=15 m，AC=25 m,∠BCM=30°,则tanθ的最大值______.

(2014年浙江省数学高考理科试题第17题)

评析例7和例8从考点来说都是最值问题.虽然从题目的形式上来说完全是2道题，但核心的解题思路其实是一致的，即最终通过相同的化归转化方式，变为求二次函数的最值问题.

例7表面看是平面向量问题，实际上

从而

通过换元得到最大值为2.

例8添加如图6所示的辅助线，可得

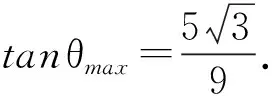
5 “传承题”之五：函数大题，永恒旋律

例9已知a∈R，函数f(x)=x3-3x2+3ax-3a+3.

(1)求曲线y=f(x)在点(1,f(1))处的切线方程；

(2)当x∈[0,2]时，求|f(x)|的最大值.

(2013年浙江省数学高考理科试题第22题)

例10已知函数f(x)=x3+3|x-a|(其中a∈R).

(1)若f(x)在[-1,1]上的最大值和最小值分别记为M(a),m(a)，求M(a)-m(a);

(2)设b∈R，若[f(x)+b]2≤4对x∈[-1,1]恒成立，求3a+b的取值范围.

(2014年浙江省数学高考理科试题第22题)

评析高考函数大题可以说是历年必考的重点题之一，并且因为其综合性强、形式多样、难度较大，往往是考生心中的“梦魇”.要抓好函数大题，必须学会抓住条件，认真分析、处理各知识点间的联系，并且要熟练掌握含参讨论、数形结合、转化回归、导数求值、函数性质等基本数学思想和相关方法性质.

例9和例10从结构上看是同一个三次函数模型，这是高中数学的典型模型，能很好地考查学生的基本函数解题素养.实际上，近3年的浙江理科数学压轴题均为三次函数含参型，可以看出命题者对此类题有所偏好.此外，这2道题在结构上更包含了一个共同元素：绝对值，差别是例9出现在了求答部分，而例10放在了题干部分，可以说是一脉相承、交相辉映，当然解法上必然也有很多相似之处.例9的2个小题层次性明显，第(2)小题比较繁琐，本质上是3个层次结构的含参讨论问题；而例10切入难度比例9更大，含参讨论出现在第(1)小题(具体求解略)，但同时作为第(1)小题的难度“补偿”，第(2)小题若能转化成“对-2-b≤f(x)≤2-b恒成立”，则可发现“M(a)-m(a)=4”这个关键点，结合第(1)小题的结论稍作讨论问题就迎刃而解.从这2道题的对比可以发现命题者在重、难点把握和平衡上的“真功夫”，也真正体现了匠心独具的一面.

总之，高考命题是一项非常严肃、复杂、技巧性强的系统工作，其本意是要考查广大应考生的基本素养和灵活应用水平.作为一线教师，若能从高考的新趋势、新特点出发，做好相关研究工作，钻研教材，钻研新的学法、考法，从高考的考法中捕捉一些特色、一些传承，进而领悟一些精髓，则必然会给我们的教学带来诸多裨益.